关于多重Bent序列集相关值分布的研究
2015-02-10常祖领丁亚男
常祖领, 丁亚男
(1.郑州大学 数学与统计学院 河南 郑州 450001;2.福建师范大学 网络安全与密码技术重点实验室 福建 福州 350007)
关于多重Bent序列集相关值分布的研究
常祖领1,2, 丁亚男1
(1.郑州大学 数学与统计学院 河南 郑州 450001;2.福建师范大学 网络安全与密码技术重点实验室 福建 福州 350007)
对多重bent序列集的构造方法进行研究,运用代数方法明确给出了多重bent序列集之间互相关值的分布.通过选取合适的bent函数,构造出互相关性较好的多重bent函数序列集,修正了一些已有的结果.
bent函数; 二元bent序列; 多重信号集; 极大互相关值
0 引言
具有良好伪随机特性和低相关性的周期序列对CDMA通信和扩频通信系统的性能具有重要作用[1-3].在CDMA通信中,每个用户都有一个指定的传播码,即周期为N的二元序列,当多个用户通过同一个通道传递信号时,对信号检测的干扰不仅来自于一个信号集中的信号,还来自于多个不同信号集中的信号,这种信号的干扰就是多重信号集之间的互相关性.作者对多重bent序列集的构造方法进行了研究,运用代数方法明确证明了不同bent序列集之间互相关值的分布情况.通过选取合适的bent函数,构造出互相关性较好的多重bent函数序列集.结果表明,在一定条件下,来自不同bent序列集的两条bent序列之间的互相关值除在某一个移位处会比较大外,在其他移位处的互相关值都不超过原始bent序列集的极大互相关值,从而构造出了更大的具有应用价值的序列集.文中还修正了一些已有的结果.
1 基本定义和性质

定义1[1]设Ca,b(τ)是两个周期为N的二元序列a={ai}和b={bi}的互相关函数,定义如下:
这里,i+τ是关于modN取值.
定义2[1]设Sj={sj,0,sj,1,…,sj,N-1},0≤j 其中,当i=j时,τ≠0,则S叫作一个(N,r,δ)信号集. 定义3[2-3]设S1,S2,…,Sk是k个(N,r,δ)信号集,且它们中的任意两个序列都是两两移位不同的,这k个信号集S1,S2,…,Sk的极大互相关值定义为 其中,当a=b时,τ≠0,则S1,S2,…,Sk是(N,r·k,Δ)多重信号集. 根据定义5,可以证明广义迹变换有如下性质[1]: (4)Parseval恒等式为 目前已有很多关于bent函数构造和性质的相关结果,详细内容可参考文献[4-9]. 满足定义7中关系的bent函数对于构造良好的多重bent函数序列集有着重要作用. 由于bent函数序列集具有非常好的互相关特性,但其序列集的容量不大,所以人们尝试用各种方法扩大bent序列集的容量.基于扩大bent序列集容量的想法,在一定条件下,通过找到合适的bent函数,给出一种扩大bent序列集容量的构造方法,使得构造出的多重bent序列集之间有较好的互相关性. 为了证明定理1,需要用到以下引理和性质. 引理3fη,θ(x)同构造方法中的构造一致,其中,η∈F2m,θ∈B,则 证明 注1这个性质是F2m上的m序列的二元组平衡性, 详细证明见文献[1]. 下面给出定理1的证明: (1)当τ=0时,δ=1, 综上可知,当β≠0时,Ca,b(τ)=-1. (2)当τ≠0时,分δ∉F2m和δ∈F2m两种情况讨论. (i)若δ∉F2m,由Parseval恒等式和乘法移位性质可得 则 因此V=Hθi∩δHθj. z=ξ1+θiσ0=(x0+x1σ0)(ξ2+θjσ0)= (x0θj+x1ξ2+ax1θj)σ0+x0ξ2+bx1θj⟹ 即Ca,b(τ)=-1±2m. (ii)若δ∈F2m,则 事实上,的确可以找到满足定义7中的bent函数集,使得按照定理1构造出来的多重bent函数序列集满足定理1中的结论. 注2定理1其实是文献[3]中定理2的改进.在文献[3]中,根据文献[3]的定理2把不同的bent序列集合并起来,声称构造了一个具有参数(2n-1,(2m-1)·2m,2m+1)的良好的多重bent序列集,即文献[3]中推论1,显然这个结论是错误的.事实上,按照文献[3]中定理2构造出的多重bent序列集之间的互相关值会很大,有可能达到2n-1.而作者则是通过选取合适的bent函数,使得序列间的互相关值达到最小,并且使得序列个数比已有的类似的序列个数都多. [1] Golomb S W,Gong Guang.Signal Design with Good Correlation: for Wireless Communications,Cryptography and Radar[M]. New York: Cambridge University Press,2005:323-381. [2] Gong Guang.Correlation of multiple bent function signal sets[C]// IEEE Information Theory Workshop on Information Theory for Wireless Networks.Solstrand,2007:1-5. [3] Gong Guang. Design of signal sets with low intraference for CDMA application in networking environment[R].University of Waterloo,CACR,2006. [4] Olsen J D,Scholtz R A, Welch L R. Bent-function sequences[J]. IEEE Transactions on Information Theory,1982,28(6): 858-864. [5] Rothaus O S. On bent function[J]. Journal of Combinatorial Theory:Series A,1976,20(3): 300-305. [6] Kumar P V. On bent sequences and generalized bent functions[D]. Los Angeles :University of Southern California,1983. [7] No J,Gil G,Shin D. Generalized construction of binary bent sequences with optimal correlation property[J]. IEEE Transactions on Information Theory,2003,49(7): 1769-1780. [8] Kumar P V,Scholtz R A,Welch L R. Generalized bent functions and their properties[J].Journal of Combinatorial Theory:Series A,1985,40(1):90-107. [9] Helleseth T, Kholosha A. On generalized bent functions[C]//Information Theory and Applications Workshop.San Diego, 2010:1-6. [10]刘古胜,朱玉明. Bent序列的相关值分布的研究[J].数学的实践与认识,2009,39(22): 140-147. (责任编辑:孔 薇) On the Distribution of Correlation Values of Multiple Bent Sequence Sets CHANG Zu-ling1,2, DING Ya-nan1 (1.SchoolofMathematicsandStatistics,ZhengzhouUniversity,Zhengzhou450001,China;2.KeyLaboratoryofNetworkSecurityandCryptology,FujianNormalUniversity,Fuzhou350007,China) The method of constructing multiple bent sequence sets was studied and the distribution of correlation values of multiple bent sequences was clearly provided by using algebraic method. By choosing appropriate bent functions, the multiple bent sequence sets with good correlation were constructed, and some existing results were corrected. bent function; binary bent sequence; multiple signal set; maximum correlation value 2014-12-21 国家自然科学联合基金资助项目,编号U13040604; 河南省教育厅科学技术研究重点项目,编号14A110022;福建省网络安全与密码技术重点实验室开放课题,编号15005. 常祖领(1976-),男,河南新乡人,副教授,博士,主要从事密码学、编码理论及序列研究,E-mail:zuling_chang@zzu.edu.cn. 常祖领, 丁亚男.关于多重Bent序列集相关值分布的研究[J].郑州大学学报:理学版,2015,47(2):1-6. TN918.1 A 1671-6841(2015)02-0001-06 10.3969/j.issn.1671-6841.2015.02.001
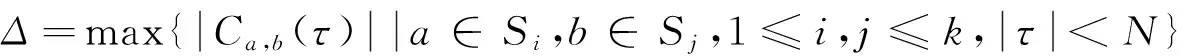







2 多重bent函数序列集之间的互相关性



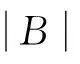
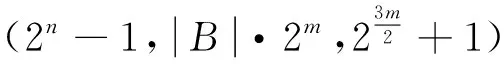

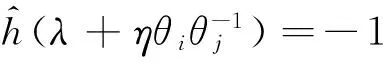
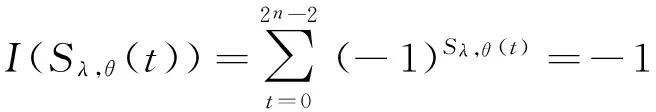
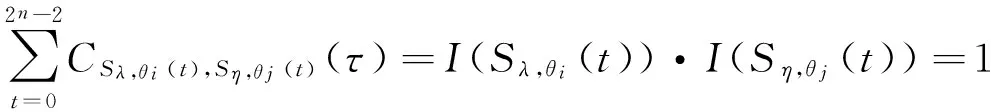
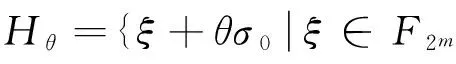

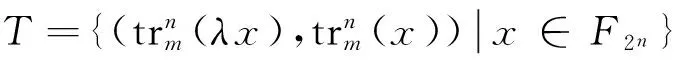


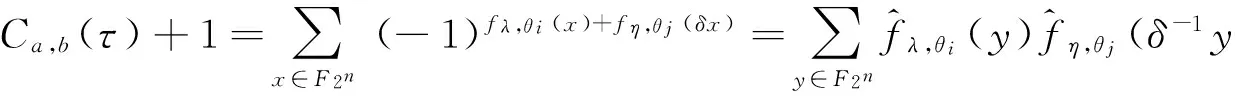
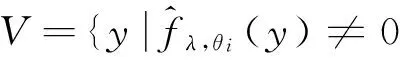
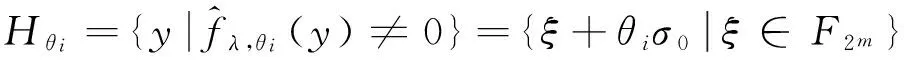
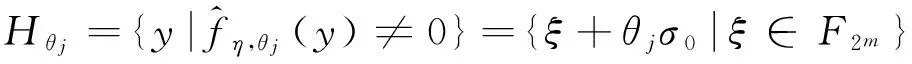
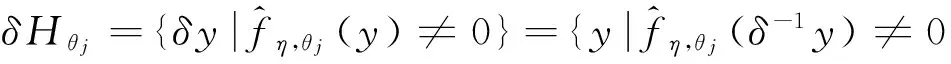
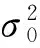
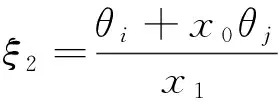
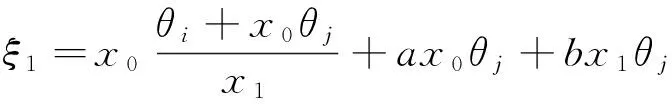



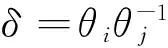
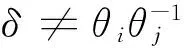
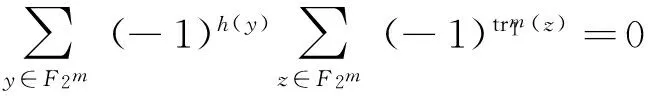
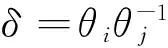
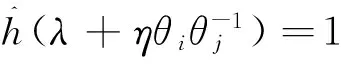





3 结论