非参数认知诊断方法：多级评分的聚类分析*

康春花 任 平 曾平飞

(浙江师范大学教师教育学院, 金华 321004)

1 引言

认知诊断评估(Cognitive Diagnostic Assessment,CDA)以认知诊断测验为载体, 采用合适的认知诊断模型对学生的知识结构进行诊断分析。在 CDA中, 被试知识状态分类准确性的影响因素众多, 其中最主要的是有效的认知诊断测验和适宜的诊断模型(Borsboom, Mellenbergh, & van Heerden, 2004)。Fu和Li (2007)总结出60多种诊断模型, 典型的如规则空间模型(Rule Space Model, RSM) (Tatsuoka,1983)、属性层级模型(Attribute Hierarchy Model,AHM) (Leighton, Gierl, & Hunka, 2004)、DINA 模型(deterministic inputs, noisy and gate model) (De La Torre & Douglas, 2004; Junker & Sijtsma, 2001)、融合模型(Fusion Model) (Hartz, 2002)等。这些认知诊断模型多为参数诊断模型。参数模型有其特有的优势, 但同时也存在一些局限性, 如参数估计过程比较复杂, 需要借助特殊软件运用EM算法或MCMC算法等通过编程来实现, 而MCMC算法耗时太长,EM 算法常在局部最优值处收敛等。此外, 参数模型往往需要大样本数据, 且属性个数又不能太多,否则就会出现参数估计不正确及模型不拟合等问题(Chiu & Douglas, 2013; 涂冬波, 蔡艳, 戴海琦,丁树良, 2010)。由此, 研究者开始探索更为简洁的非参数方法, 因为相比参数方法, 非参数方法具有受限较少、假设条件较弱、计算简便、在专业的统计软件包就能完成等优势。

在非参数诊断方法的研究中, Henson等人提出了属性合分的思想(Henson, Templin, & Douglas,2007), 该思想简明易了, 然而其获得决断值的过程较为复杂, 需要借助其它参数模型先获得项目参数和被试参数信息, 未能起到非参数方法易于操作的效果。2008年, Ayers等人对属性合分进行标准化, 采用标准化的能力向量来描述被试对各属性的掌握情况(Ayers, Nugent, & Dean, 2008; Nugent,Ayers, & Dean, 2009), 属性合分标准化的思想消除了因各属性考察次数不同而造成的属性合分不可比问题。Chiu等人(Chiu, Douglas, & Li, 2009)也进一步借用属性合分的思路, 提出属性合分的聚类分析方法, 通过模拟研究比较了基于不同初始值选取方法的 K-means聚类法和基于不同距离度量方法的系统聚类法(Hierarchical Agglomerative Cluster)的表现。此外, 其近年研究表明惩罚性汉明距离(Penalized Hamming Distance)可依据项目类型的不同, 对猜测和失误分别设置权重, 其判准率可与参数模型媲美(Chiu & Douglas, 2013)。然而, 该研究中, 由于数据模拟是通过 DINA模型产生, 其分类结果的好坏是以DINA模型的最大似然估计的结果为基准。

非参数诊断方法已有一些研究基础, 然而这些方法都是基于0-1计分提出的, 不满足结构化反应题采用多级计分的实践应用情境。2001年教育部《基础教育课程改革纲要(试行)》提出：为完善考试管理制度, 考试内容应加强与社会实际和学生生活经验的联系, 重视考察学生分析问题、解决问题的能力。为此, 在许多大型测评和考试项目中, 都出现了诸如作文、简答、论述等“结构化反应”题, 因为这类题型更能反应学生对知识的分析、综合、应用、评价等方面的能力。这种题型中, 不仅题目测量的属性有多个, 而且评分者采用分步给分的方式来评价被试的作答(Kim, Walker, & McHale, 2010),因此被试在每个题目上的得分是连续取值的, 在这种情况下, 若仍然使用 0-1计分的诊断方法, 则会损失一部分数据信息, 从而影响诊断和分类的效果。

针对参数诊断模型的局限性, 而非参数研究仅停留在 0-1计分阶段, 为满足目前测评与考试的实践需求, 本文拟将聚类诊断分析这种简单易行的非参数诊断方法拓展至多级评分, 同时探讨样本容量、失误率及属性层次结构对该方法的诊断正确率的影响。研究包括4个部分：0-1计分聚类方法简介;多级计分聚类方法的拓展; 模拟研究; 实证研究。

2 0-1计分聚类诊断方法简介

2.1 被试属性合分向量和能力向量的计算

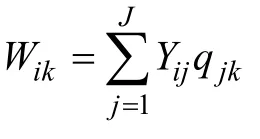
假设3个属性之间相互独立, 测验Q阵如表1所示。若被试i在测验的7道题目的作答反应向量为(1,1,1,0,1,0,0), 则根据合分向量计算公式, 被试i的属性合分W= (2,1,2)。各属性考察的题目数量向量为(4,4,4), 因此被试i的能力向量W= (1/2, 1/4, 1/2)。

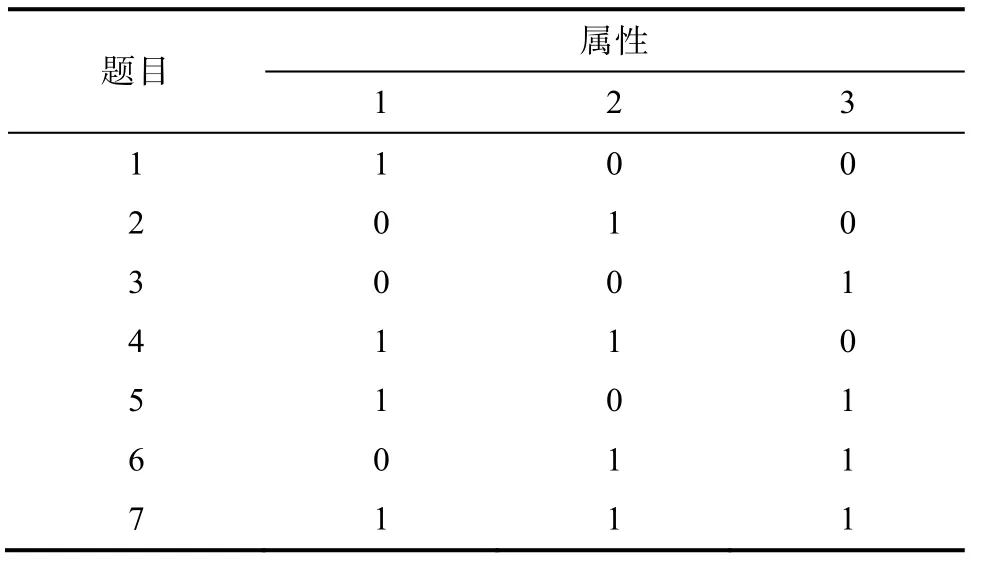
表1 含3个属性的测验Q阵

2.2 K-means算法

聚类分析就是将数据对象分成多个类, 使同类中的对象相似度最大, 不同类间的对象相异性最大。k-means算法是最常用和最典型的算法之一, 它采用距离作为相似性的评价指标, 认为两个对象的距离越近, 其相似度越大。k-means的优点在于能快速的收敛及易于实现, 其核心思想是把N个数据对象划分为 M 个聚类, 使每个类内的数据点到该类中心的平方和最小, 具体算法如下：

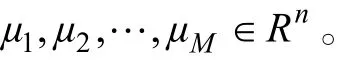
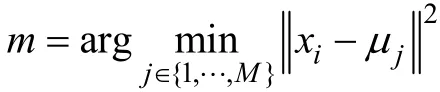
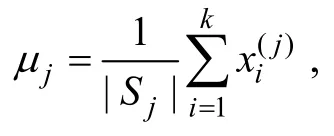
4)重复步骤2和3, 直至聚类中心不再变化。

2.3 K-means中心初始值的选取

K-means算法对中心初始值的依赖性较大, 因此初始值的选取非常重要。CDA的目的是根据被试的观察反应模式(Observed Response Patterns, ORP),把其划分到相应的理想掌握模式(Ideal Master Pattern,IMP)中。因此, 采用聚类分析对被试进行分类与诊断时, 可根据测验所考察的属性层级关系, 得到所有符合逻辑的IMP, 则可将IMP对应的能力向量作为聚类中心初始值(Ayers et al., 2008; Nugent et al.,2009)。

2.4 0-1计分聚类诊断方法的步骤

根据K-means算法的具体过程, 在CDA中, 其聚类分析思路如下：

1)根据属性层次关系, 得到IMP, 计算IMP对应的能力向量, 作为K-means聚类初始中心;

2)根据被试 ORP计算出被试能力向量(如 2.1所示), 计算被试能力向量与各聚类中心的距离,把被试分配到最近的聚类中心;

3)所有被试分配完成后, 重新计算K-means聚类中心;

4)基于过程 3)得到的聚类中心, 重新分配被试到距离最近的中心, 重复该过程直到每个被试不再重新分配为止。

3 0-1计分方法的拓展：多级计分的聚类诊断分析

基于 0-1计分聚类诊断方法的思路, 研究者将其拓展为多级计分的聚类诊断方法(Grade Response Cluster Diagnostic Method, GRCDM)。假设测验考察了4个属性, 用A1、A2、A3、A4表示, 其属性层次关系为图1所示, 由图1得到的项目属性关联矩阵Q如表2所示, 则GRCDM的核心概念及分析思路如下(步骤和初始值的选取与0-1计分相同, 不再赘述)。

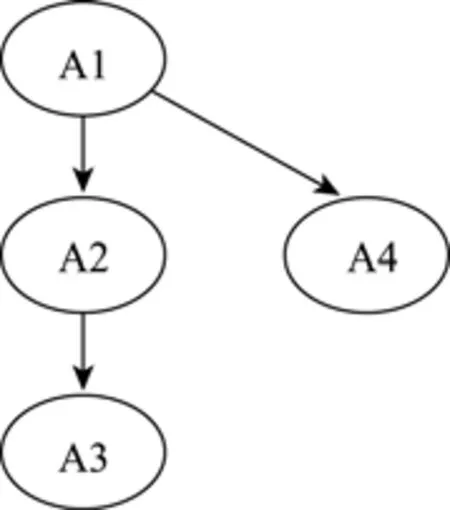
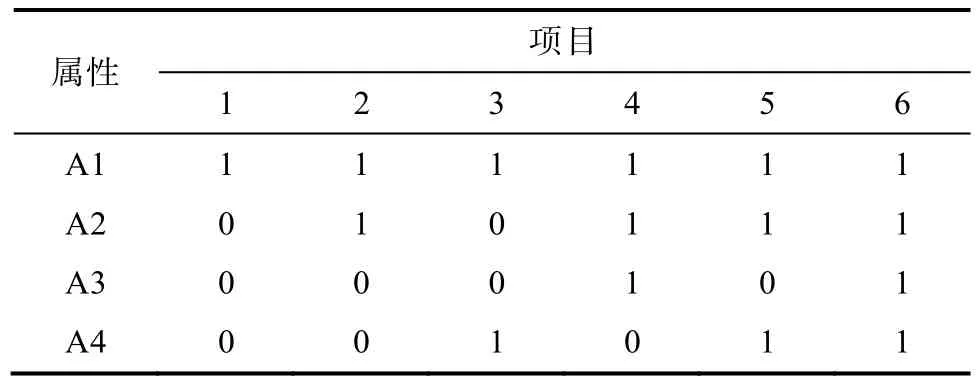
表2 图1属性层次关系对应的Q矩阵

3.1 理想反应模式的计算

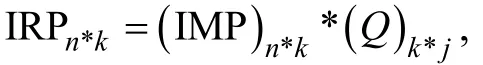
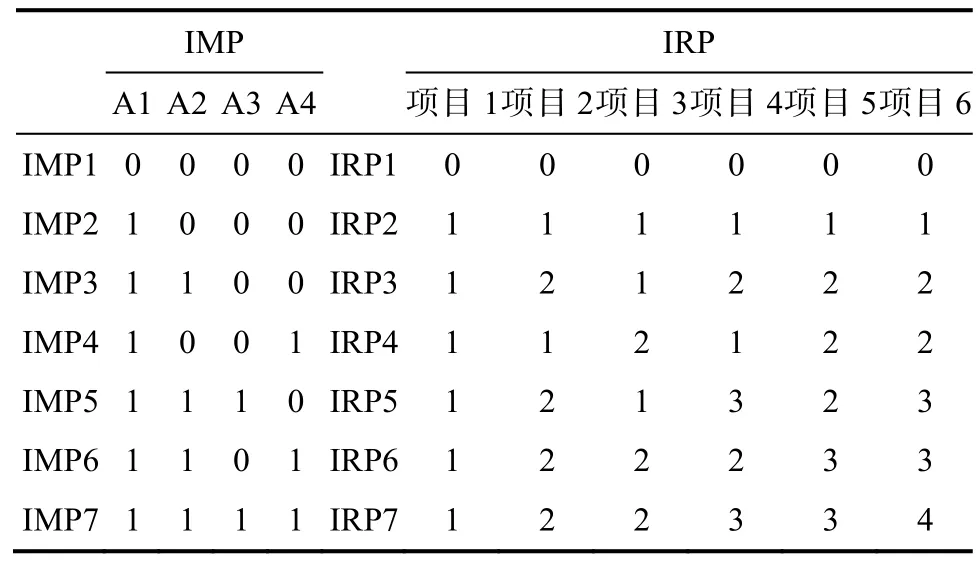
表3 图1和表2对应的IMP与IRP

3.2 属性合分和能力向量的计算方法

3.2.1 多级计分的属性合分思路

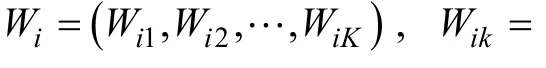
表2阵中, 从第1题到第6题, 满分分值为1、2、2、3、3、4。以第6题为例, 说明题目得分不同时, 在各属性合分上所累加的分数, 即ρ值的计算。第6题满分4分, 当被试i得1分时, 属性A1掌握概率为100%, 属性A1的合分加1分, 即ρ = 1。当被试得 2分时, 被试可能掌握的属性组合是 A1A2或 A1A4, 掌握属性A1的概率为 100%, 掌握属性A2、A4的概率为50%, 属性A1的合分加1分, 属性A2、A4的合分各加0.5分。当被试得3分时, 被试可能掌握的属性组合是A1A2A3或A1A2A4, 掌握属性A1的概率是100%, 掌握属性A2的概率是100%, 掌握属性 A3和 A4的概率分别为 50%, 则属性A1和A2合分分别加1分, 属性A3和A4合分分别加0.5分。当被试得4分时, 掌握4个属性的概率都为100%, 则 4个属性合分分别加1分。如此, 被试在各题上的得分模式时, 各属性的贡献率ρ取见如表4所示。有了ρ值, 则根据被试的在所有题目上的反应模式, 就可以得到被试的属性合分向量 W, 即被试的属性合分向量中的各元素 W为被试在所有题目中所得到的第k个属性的ρ值总和(每道题目得不同分数时, 第k个属性的ρ值不同)。k上的合分,

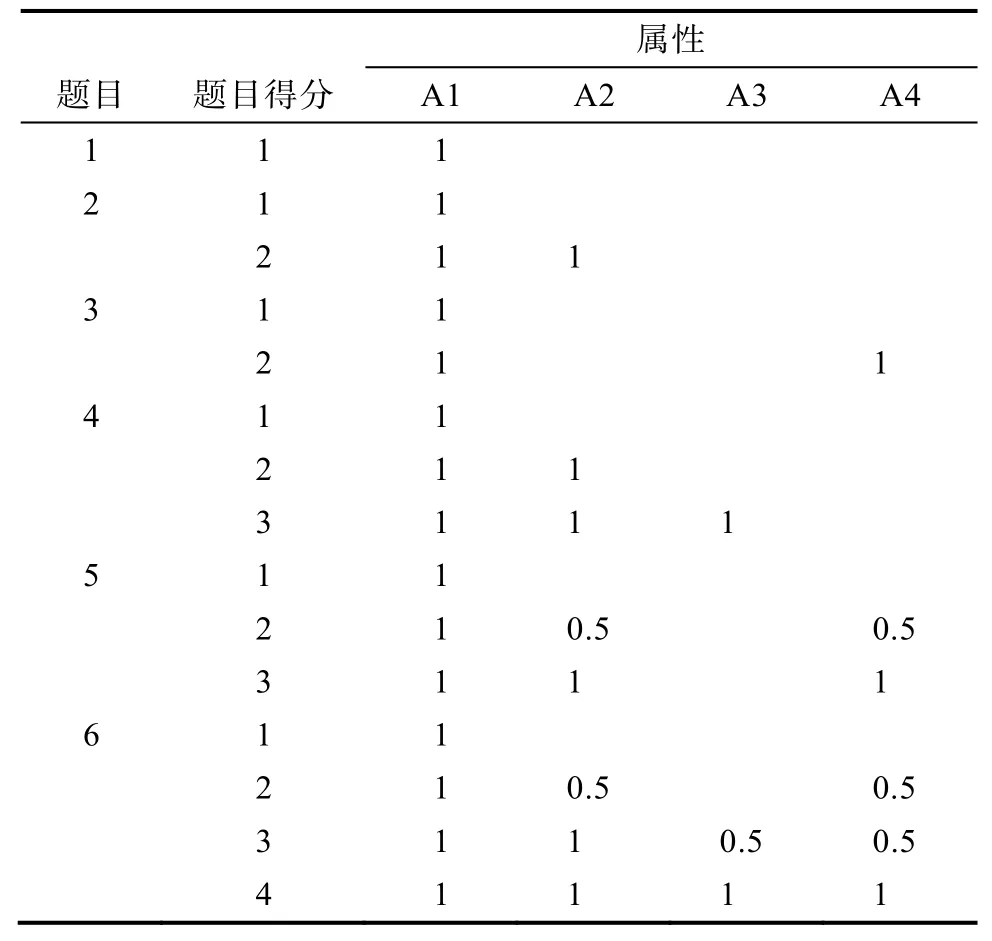
表4 ρ值表

3.2.2 能力向量的计算

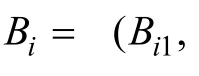
基于上述属性合分向量和能力向量的计算方法, 当未发生失误作答时, IRP所对应的各属性合分W和能力值B见表5。

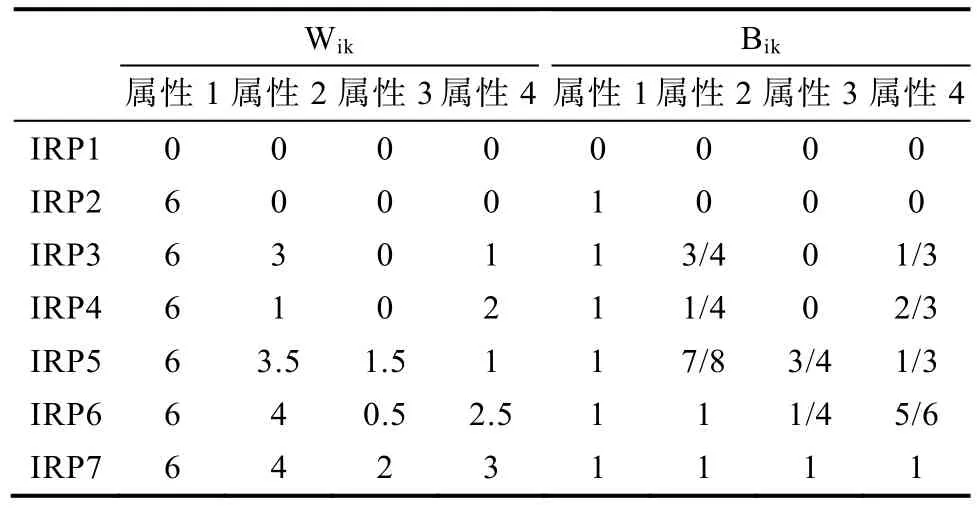
表5 表3所示IRP对应的Wik和Bik

4 模拟研究

4.1 研究目的

基于GRCDM, 采用K-means算法对被试进行诊断分类, 以考察其适用性。在固定属性个数、被试知识状态分布的情况下, 探讨属性层次结构, 样本容量、失误率对判准率的影响。

4.2 研究方法

4.2.1 研究设计

在知识状态为均匀分布、属性个数为7个的情况下, 研究包含4种属性层次结构(线型、收敛型、发散型、无结构型, 见图2)、3种样本容量(100人、500人、2000人)、3种失误率(5%、10%、20%)的4×3×3的交叉设计, 共36个试验, 每个试验重复30次以减少误差。4种结构下的简化Q阵分别包含7、8、25、64题。罗欢、丁树良、汪文义、喻晓锋和曹慧媛(2010)认为无结构型64题太多, 可剔除含属性较多的题目, 本文无结构型选22题, 只包含测量1到3个属性的题目。由此, 各层次结构下的Q矩阵如表6～表9所示。

4.2.2 被试观察反应模式的模拟

4.2.3 被试分类与诊断

首先, 通过3.2介绍的方法得到各被试ORP所对应的能力向量, 然后计算出IMP对应的能力向量作为初始聚类中心, 接着按照 2.4的步骤对被试进行聚类分析, 得到被试的知识状态。

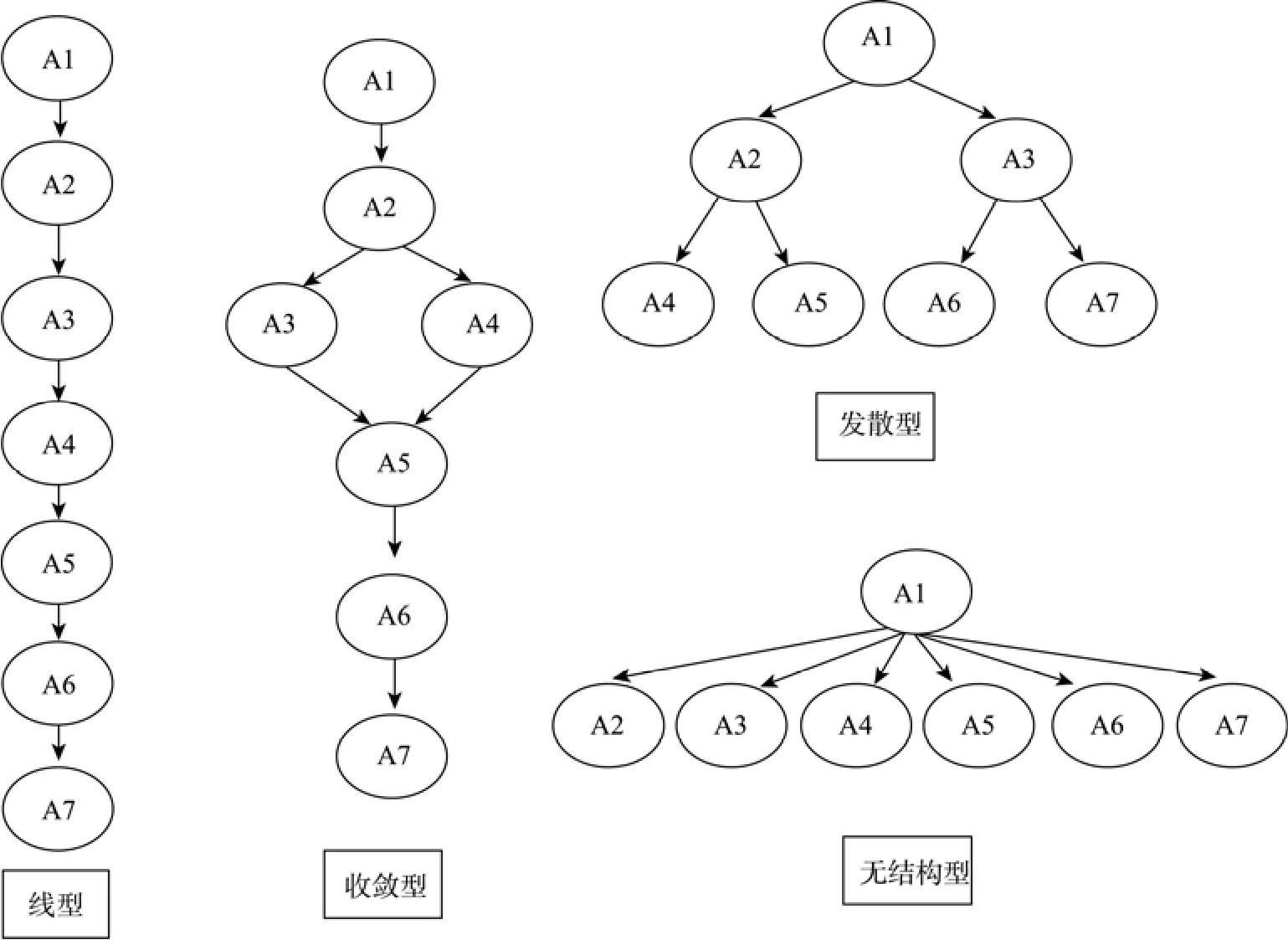
图2 含7个属性的四种属性层次结构

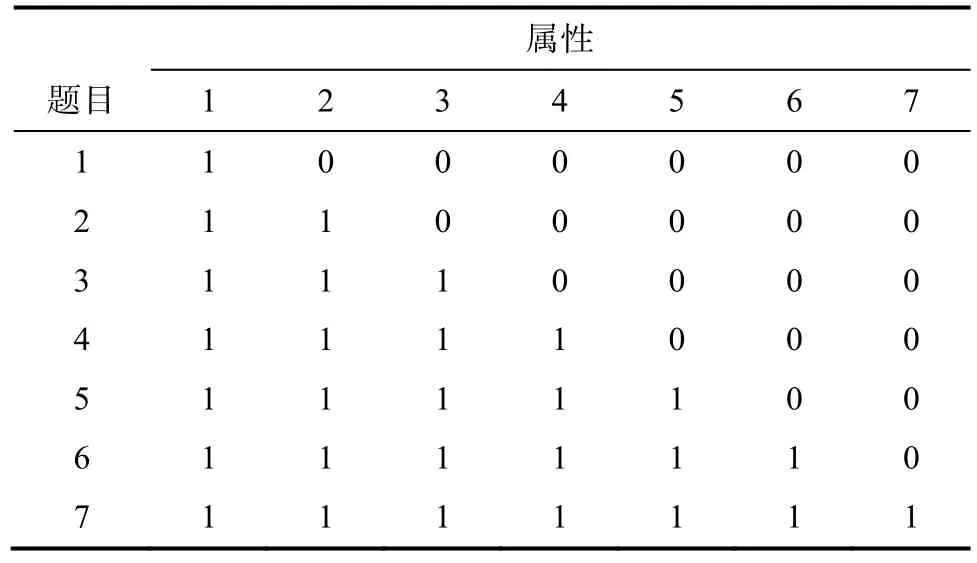
表6 Q矩阵(线型)

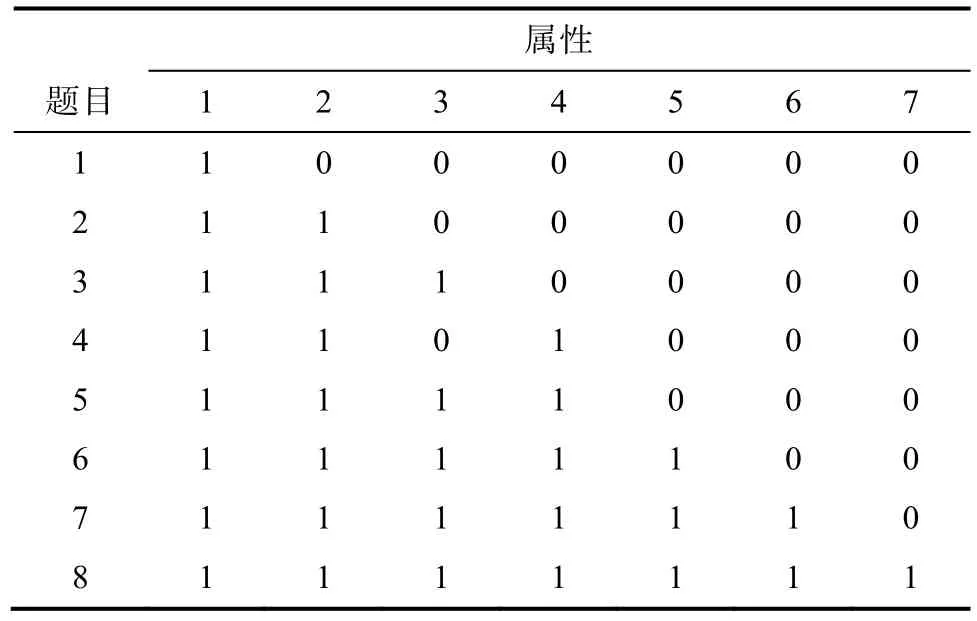
表7 Q矩阵(收敛型)

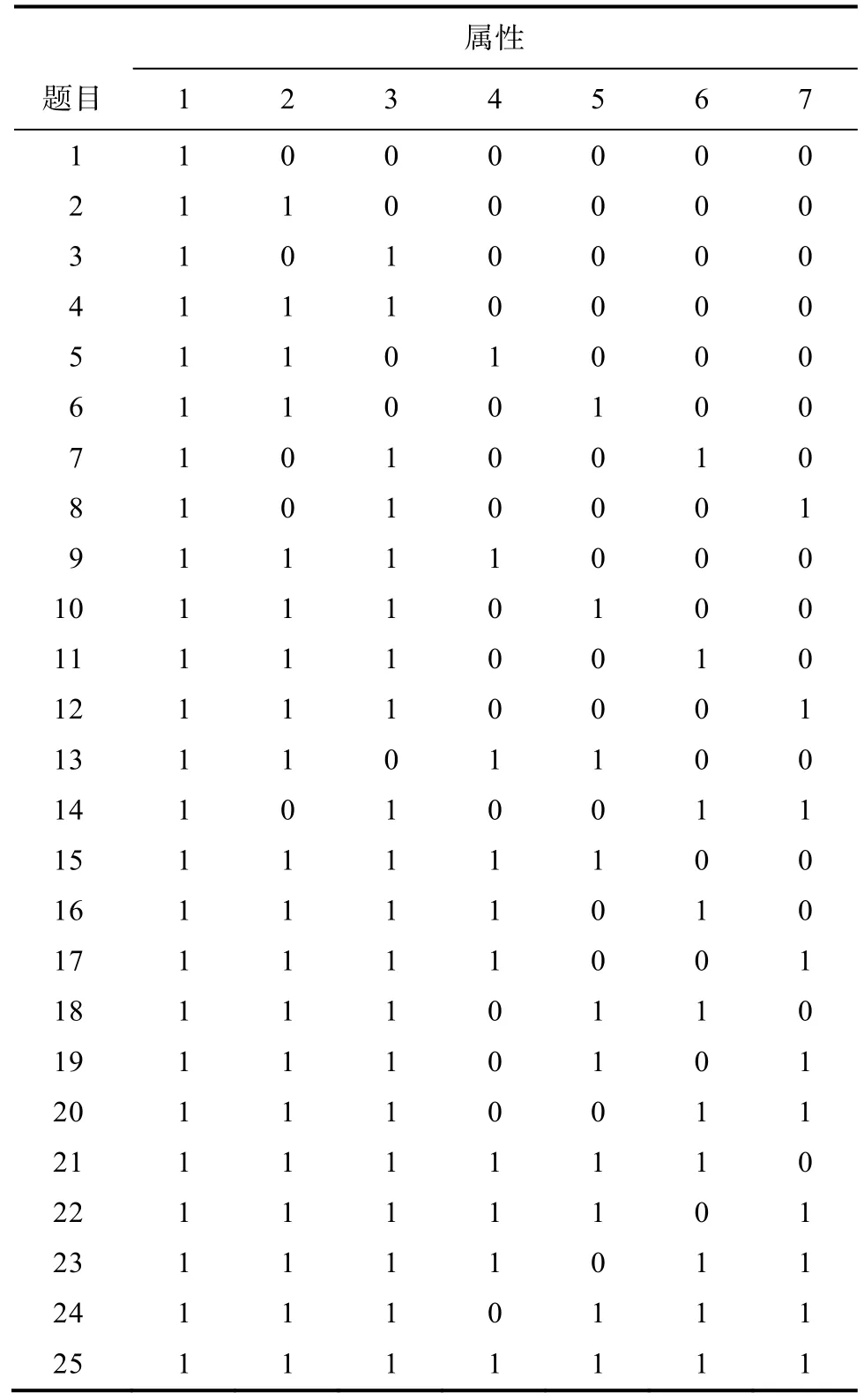
表8 Q矩阵(发散型)

以上模拟过程均通过matlab 7.0编程实现。

4.2.4 评价指标

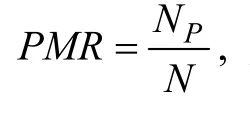
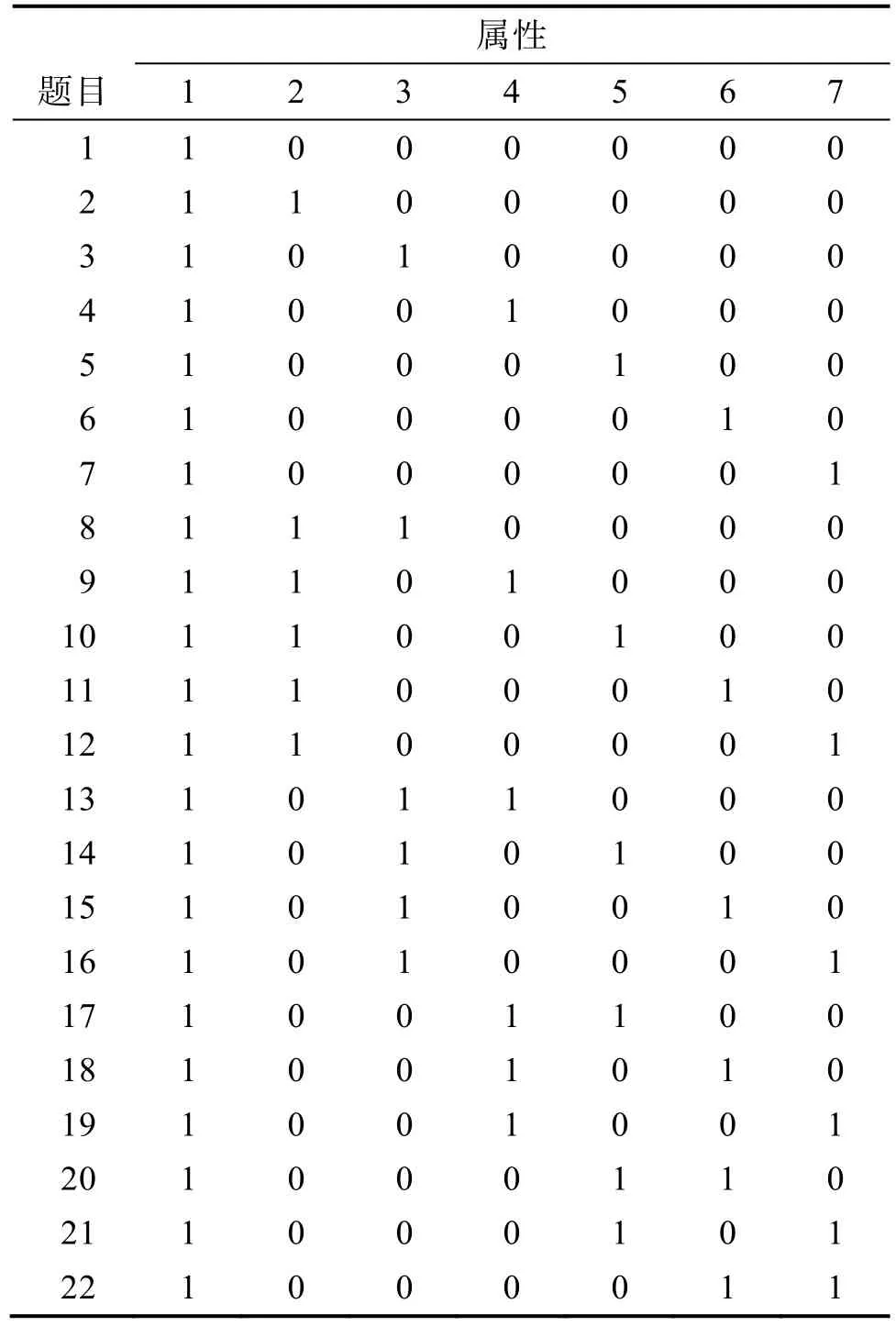
表9 Q矩阵(无结构型)

4.3 研究结果

4.3.1 GRCDM具有很高的边际判准率和模式判准率

表10为GRCDM在各实验条件下的PMR和MMR均值(重复30次)。从表中可以看出, 该方法不仅具有很高的边际判准率, MMR介于0.982到1之间, 而且还具有较高的模式判准率, 失误率为5%时, 收敛型的PMR为1, 随着失误率的增高, 模式判准率虽有下降的趋势, 但其值仍然较高, 即使在无结构型、样本容量为100、失误率为20%时, 模式判准率的最低值也能达到0.815。可见, GRCDM具有较强的稳定性与适用性。

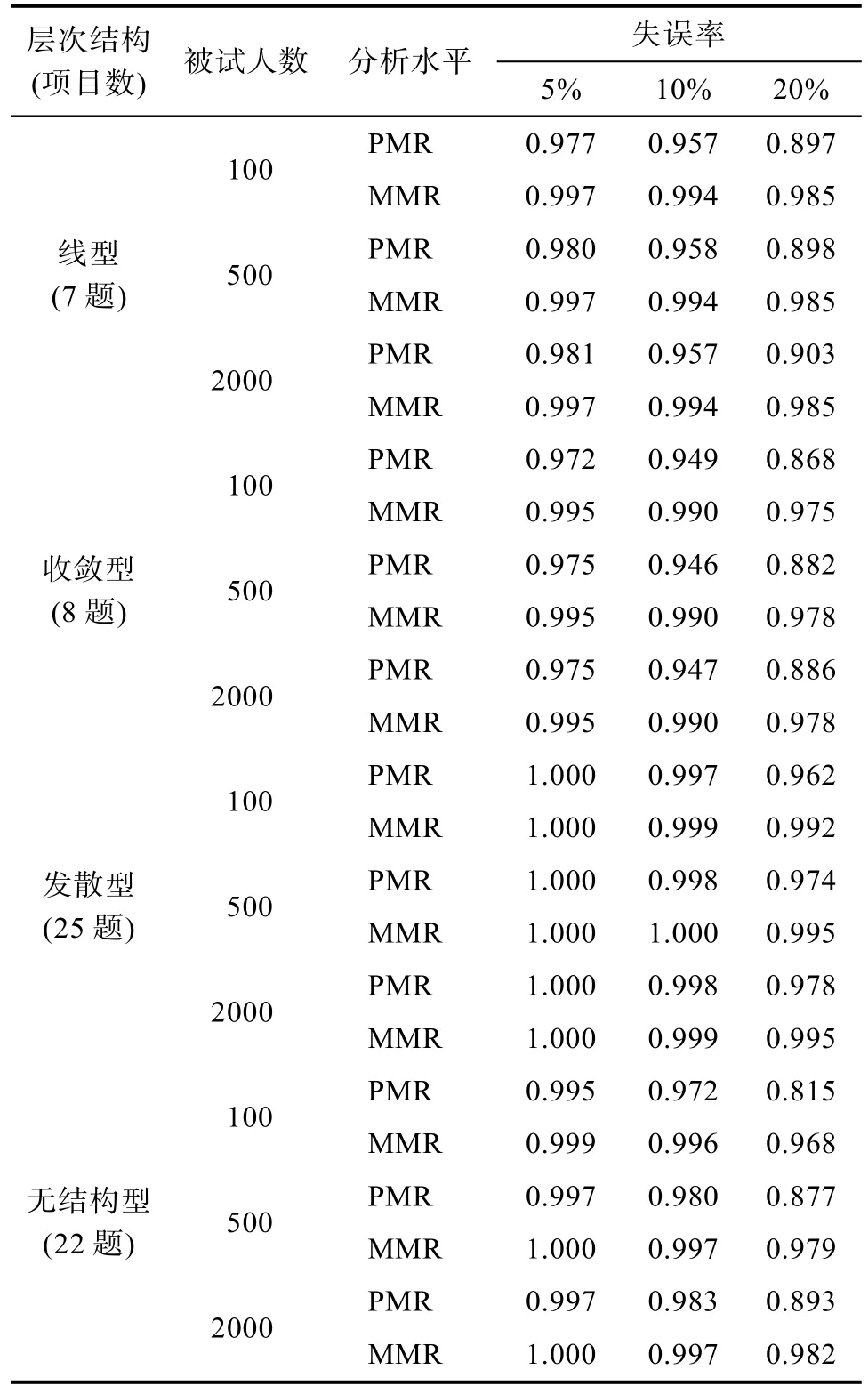
表10 GRCDM在各实验条件下的PMR和MMR均值

4.3.2 样本容量、失误率和层次结构对PMR影响的三次交互效应显著

由于各条件下, MMR均值都很高, 因此, 本文更关心各条件下 PMR的变化。为探讨失误率、层次结构、样本容量对 PMR的影响, 采用方差分析对实验数据进行分析发现：样本容量、失误率和层级结构主效应均显著(F(2,1044) = 53.647, p<0.001,η= 0.093; F(2,1044) = 3016, p<0.001, η= 0.852;F(3,1044) = 688.256, p<0.001,η= 0.664); 样本容量与失误率、样本容量与层次结构、失误率与层次结构的两次交互效应均显著(F(4,1044) = 32.883,p<0.001, η=0.112; F(6,1044)= 17.477, p<0.001, η=0.091; F(6,1044) = 216.599, p<0.001, η= 0.555); 三因素的三次交互效应也显著(F(12,1044) = 11.38,p<0.001, η= 0.116)。可见, 三因素对PMR的影响不是独立发生的, 而是相互关联、交叉进行的, 应对三次交互效应进一步进行分析, 以揭示其对PMR影响的内部机制。

(1) 失误率为5%和10%时, PMR不受样本容量的影响

已有研究表明, 失误率的增加必然导致诊断正确率在一定程度上的下降(田伟, 辛涛, 2012; 祝玉芳, 丁树良, 2009), 因此, 本研究宜在失误率的不同水平上, 分析样本容量与层次结构的简单交互效应, 以探测三因素对PMR的交叉影响。

结果表明：失误率为 5%和 10%时, 样本容量不存在主效应、样本容量与层次结构之间不存在交互效应(F(2,348) = 2.48, p>0.05; F(6,348) = 0.30,p>0.05; F(2,348) = 1.292, p>0.05; F(6,348) = 1.747,p>0.05), 只有层次结构主效应显著(F(3,348) =171.685, p<0.001, η= 0.579; F(3,348) = 281.192,p<0.001, η= 0.708)。对层次结构的事后比较发现：失误率为5%时, 无结构型和发散型的PMR均值无显著差异, 其它各结构均差异显著(发散型、无结构型>线型>收敛型); 失误率为 10%时, 各层次结构间的PMR均值均显著, 且发散型>无结构型>线型>收敛型, 结果见表11、表12。

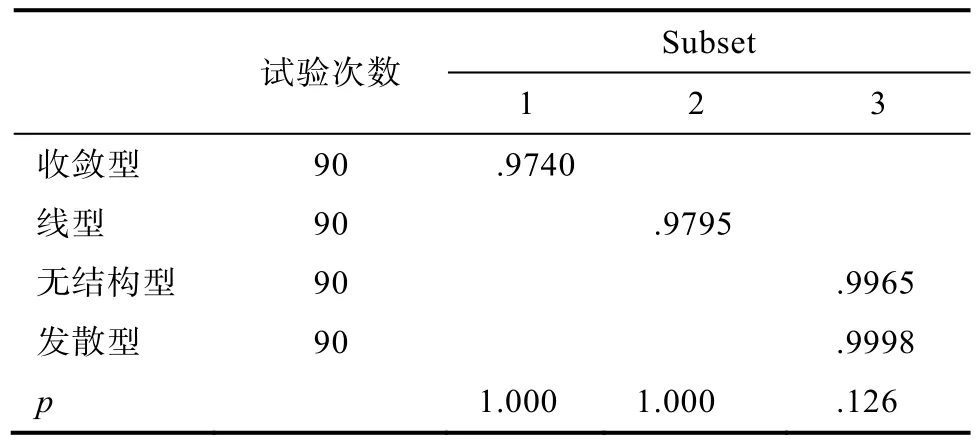
表11 层次结构事后多重比较 Scheffe (失误率=5%)

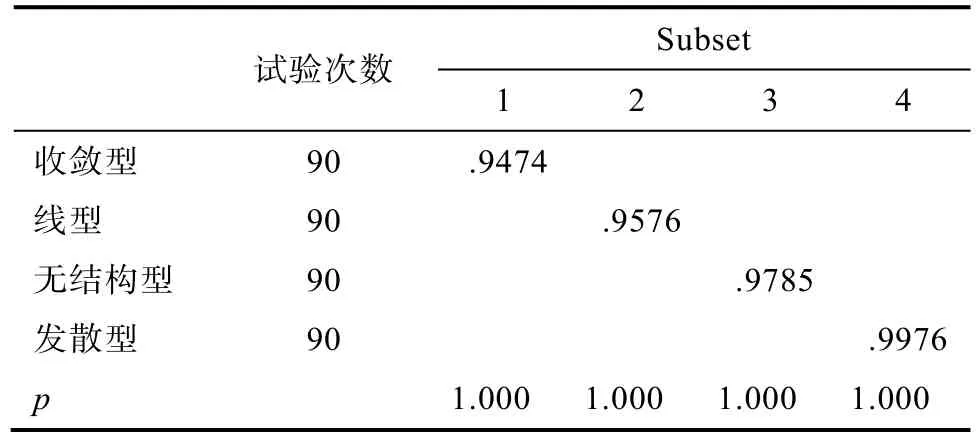
表12 层次结构事后多重比较 Scheffe (失误率=10%)

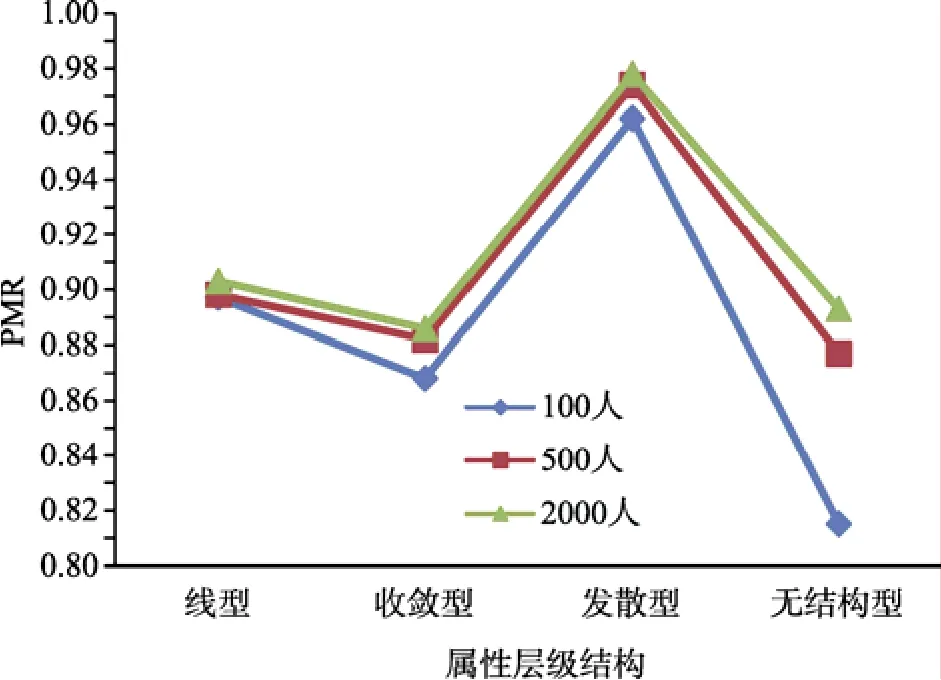
图3 样本容量与层次结构交互效应图

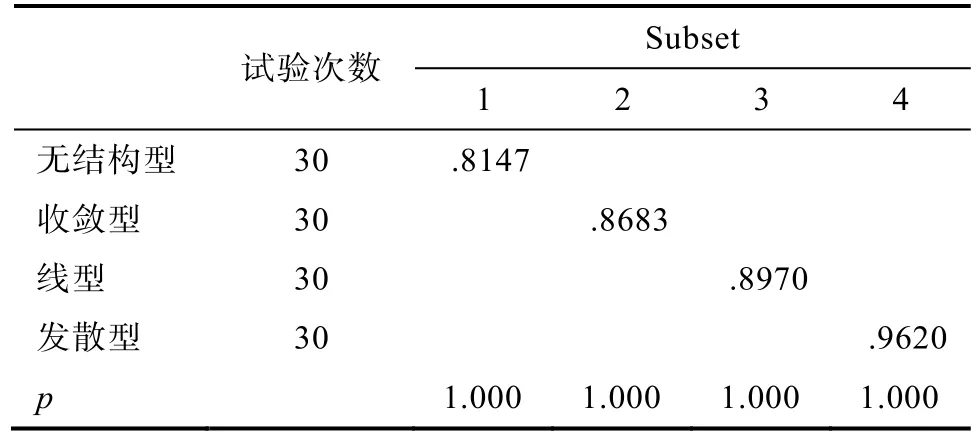
表13 Scheffe (失误率 = 20% & n = 100)

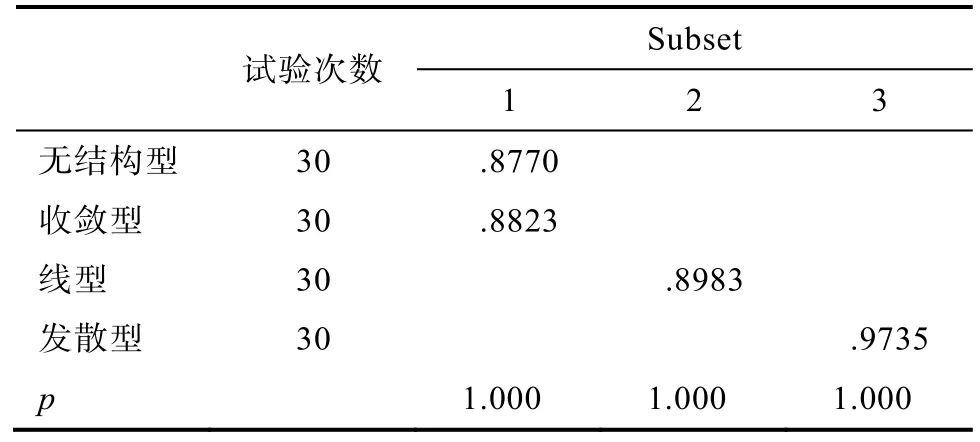
表14 Scheffe (失误率 = 20% & n = 2000)

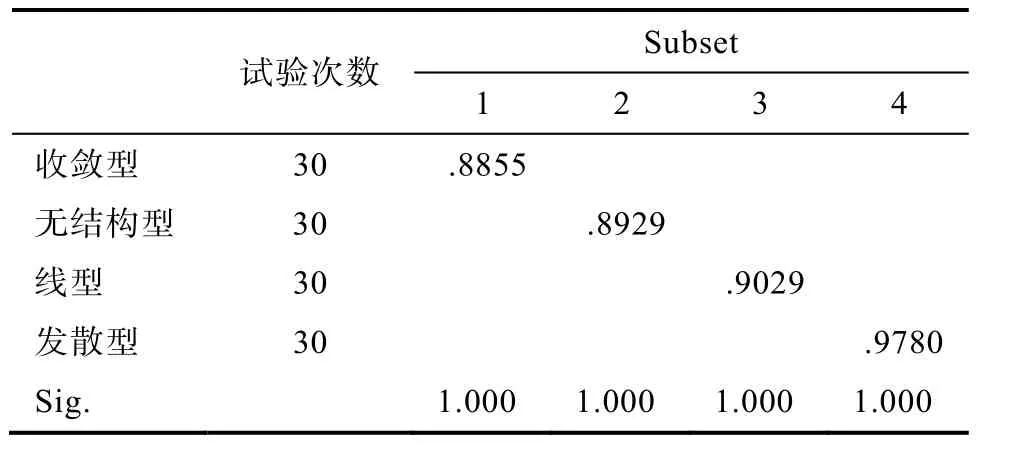
表15 Scheffe (失误率 = 20% & n = 100)

(2) 失误率为20%时, PMR受样本容量与层次结构的交互影响

失误率为20%时, 样本容量和层次结构的主效应以及两者之间的交互效应均显著(F(2,348) =59.553, p<0.001, η= 0.254; F(3,348) = 440.536,p<0.001, η= 0.792; F(6,348) = 19.646, p<0.001, η=0.253, 见图 3)。

固定样本容量对层次结构进行简单简单效应发现：样本容量为100人、500人和2000人时, 层次结构间PMR均值差异均显著(F(3,116) = 95.320,p<0.001, η= 0.711; F(3,116) = 311.936, p<0.001, η=0.890; F(3,116) = 1177.518, p<0.001, η= 0.968),但差异方向和强度均不同(见表13～表15)。表13-15表明样本容量为 100人时, 发散型>线型>收敛型>无结构型; 样本容量为500人时, 发散型>线型>收敛型和无结构型; 样本容量为2000人时, 发散型>线型>无结构型>收敛型。

固定层次结构对样本容量进行简单简单效应发现：线型和收敛型时, 样本容量的简单简单效应均不显著(F(2,87) = 1.063, p>0.05; F(2,87) = 3.5,p>0.05), 而在发散型和无结构型时, 样本容量的简单简单效应均显著(F(2,87) = 13.176, p<0.001, η=0.232; F(2,87) = 68.103, p<0.001, η= 0.610), 且均为2000人、500人>100人, 但2000人和500人之间差异并不显著, 见表16～表19。

表16 Scheffe (失误率 = 20% & 层次结构=线型)

表17 Scheffe (失误率 = 20% & 层次结构=发散型)

表18 Scheffe (失误率 = 20% & 层次结构=收敛型)

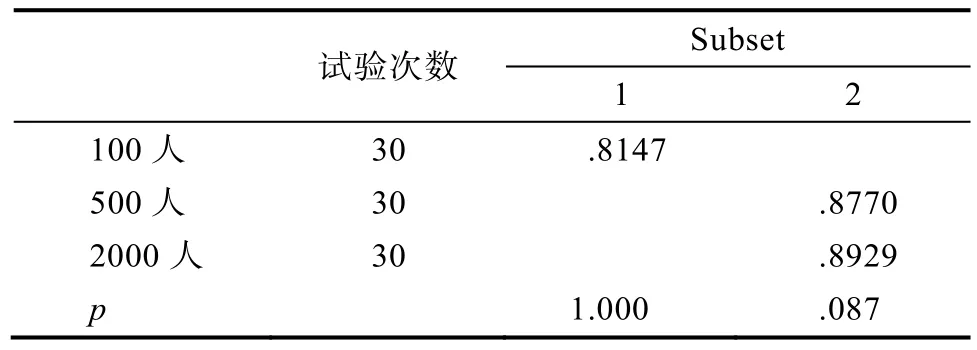
表19 Scheffe (失误率 = 20% & 层次结构=无结构型)

5 实证研究

5.1 研究目的

为验证GRCDM在实践中的效能, 采用GRCDM对小学行程问题解决的认知诊断数据进行分析(康春花, 2011), 考察其在实践中的适用性。

5.2 数据来源

数据来源于康春花(2011)的小学应用题认知诊断评估数据, 为 1240名学生(好、中、差学校人数各为135、853 和252 人)在17道题上的原始得分。测验考察了8个认知属性：基本算术运算(A1)、基本图式(A2)、多步运算和等级复杂性(A3)、复杂图式(A4)、识别隐含条件(A5)、关系表征(A6)、图式表征(A7)、项目代数性(A8)。8个属性的层级关系及测验Q矩阵见图4和表20(康春花, 辛涛, 田伟, 2013)。

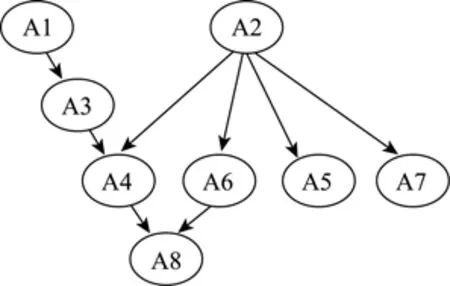
图4 8属性的层次关系

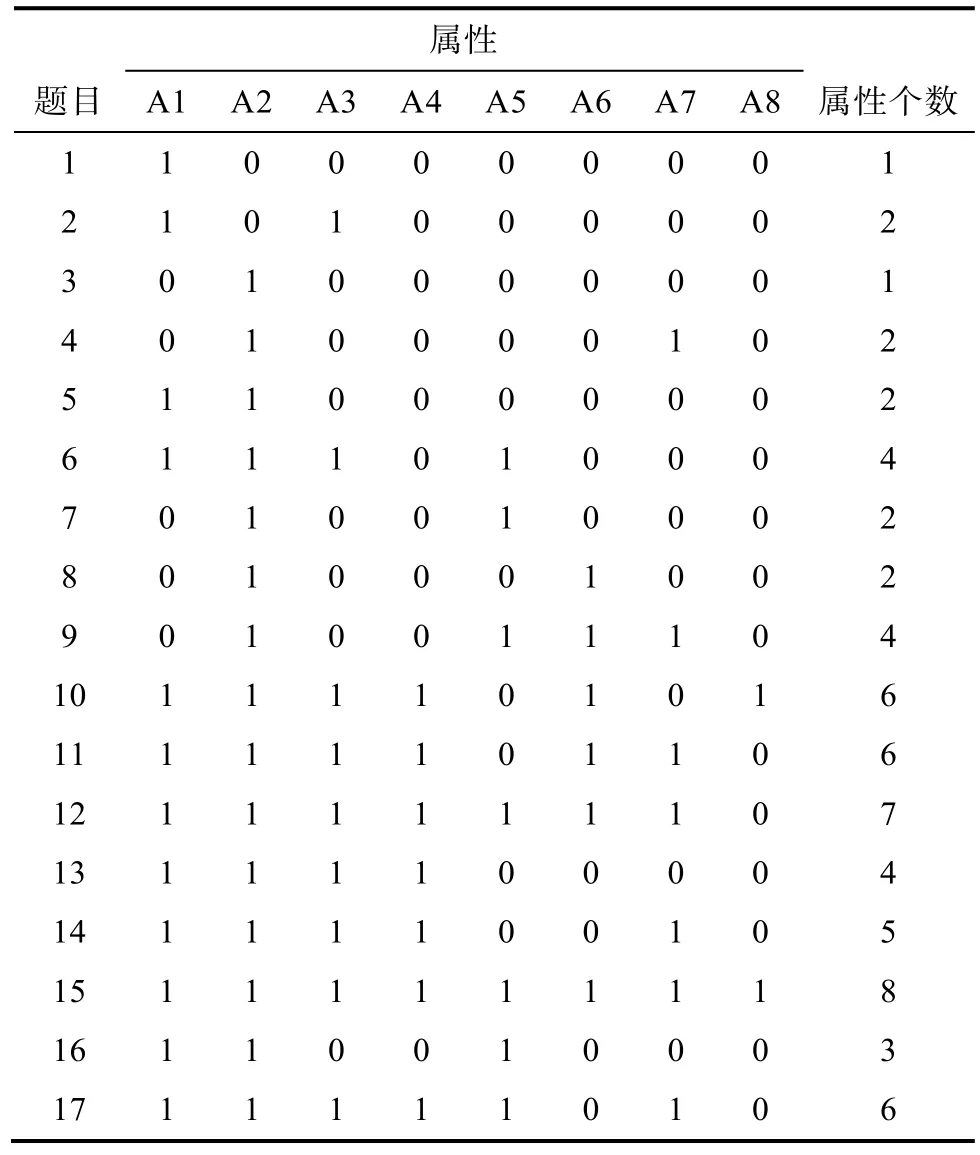
表20 Q矩阵

5.3 过程与方法

GRCDM在实证研究中的思路为：(1)根据图4属性层次结构, 可得到39种IMP; (2)依据3.1所示得到IMP对应的IRP; (3)根据3.2.1所示求得不同得分模式下各属性对合分的贡献值ρ, 从而得到IRP对应的能力向量; (4)依据1240名被试在17道题上的ORP, 按 3.2所示, 得到他们的能力向量; (6)以 39种 IMP所对应的能力向量为初始聚类中心, 对1240名被试的原始能力向量进行聚类, 把他们归类到39种IMP中。

程序与软件：matlab 7.0自编程序实现聚类分析与诊断; SPSS 19.0和EXCEL 2007实现效度验证分析。

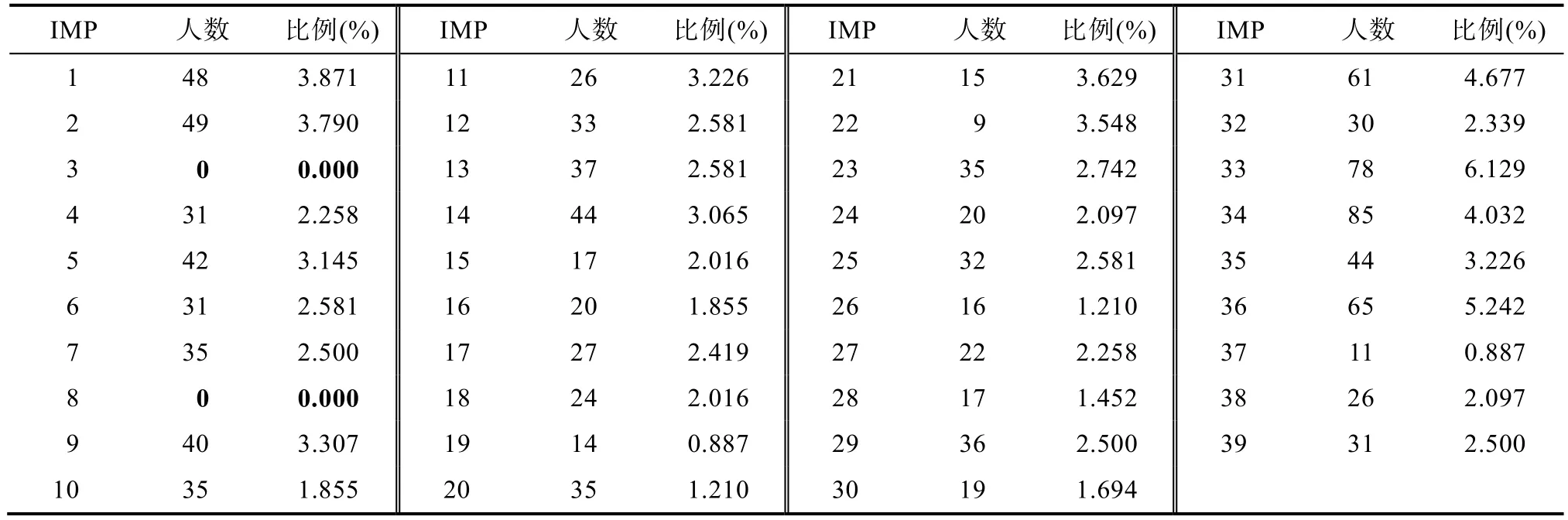
表21 归类结果

5.4 结果

5.4.1 GRCDM的分类结果

GRCDM对1240名被试的分类结果见表21：该方法把1240名被试分到39种掌握模式中的37种,有两个模式(3和8)为空, 相比多级规则空间的分类结果(该结果有8个模式为空) (康春花, 2011), 更加均匀。

5.4.2 属性通过率与属性性质相匹配

基于表7的结果, 可得到各属性的掌握人数百分比(见表22)。在两个先决条件属性A1、A2上, 被试表现很好, 随着复杂行程问题的出现, 在完成复杂任务的基本条件A1、A2、A3、A4中, 其错误主要出现在 A4上。此外, 被试的认知错误主要以认知过程属性为主, 如 A5、A7和 A8出现的错误较多。各属性的难度趋势与各属性的性质是相匹配的,从易到难依次为程序性知识属性、陈述性知识属性、认知技能或策略属性。可见, 该方法在实证中也有较好的分类效果。

表22 各属性掌握人数百分比(%)

5.4.3 属性通过率的学校类型差异

按康春花等人(2013)的研究, 学校类型(好、中、差)可以作为一个外部客观标准, 用来分析诊断评估的外部效度。由于被试在单个属性上的通过百分比, 可看作是属性通过率, 如果把这些比率看作是各属性得分的均值, 则可利用方差分析对学校类型差异进行检验。本研究中, 各学校类型在各属性上的属性通过率及其差异见图5。

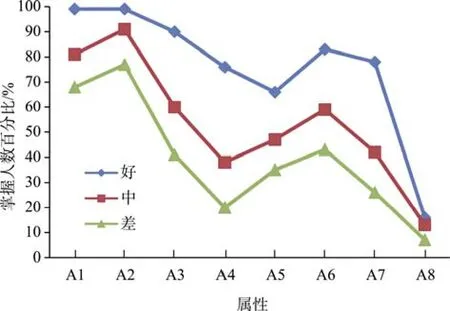
图5 好、中、差学校在各属性上的掌握人数百分比

方差分析发现, A1-A8的属性通过率均存在学校类型主效应(F(2,1237) = 26.554, p<0.001, η= 0.041;F(2,1237) = 28.268, p<0.001, η= 0.044; F(2,1237) =48.504, p<0.001, η= 0.073; F(2,1237) = 65.604,p<0.001, η= 0.096; F(2,1237) = 18.049, p<0.001, η=0.028; F(2,1237) = 30.227, p<0.001, η= 0.047;F(2,1237) = 52.772, p<0.001, η= 0.079; F(2,1237) =4.83, p<0.001, η= 0.008), 并且, 除了在 A8 上, 好、中>差外, 其余均为好>中>差, 但差异强度有所不同, 这可以从图5很直观的看出。在较易和较难的属性上(A1、A2和A8), 差异程度较低, 而在其它5个属性上, 差异程度有所增加, 并且表现在好学校与中等学校差异程度扩大, 而中等学校与差学校虽有差异, 其差异程度相对较小。

6 讨论

在统计学中, 相比参数方法, 非参数方法具有假设条件少、不受限于样本容量、计算简便、更具稳健性且适用面广等优势(胡竹菁, 2010)。本研究所得结果可为CDA方法选择和实践应用提供参考和建议。

6.1 GRCDM具有很高的判准率

GRCDM 充分利用了连续得分的数据信息, 操作简单, 便于理解、只需属性层次关系和Q矩阵、无需估计参数、对样本容量无依赖、耗时短、且具有较好的稳健性。模拟研究表明, 在每种试验条件下(共36种), 重复30次试验的平均PMR和MMR值均很高(PMR：95.35%; MMR：99%)。为进一步说明GRCDM的稳定性和适用性, 加入与前人研究相同条件下的比较(田伟和祝玉芳等人对等级反应模型的规则空间方法和AHM方法(包括A方法、B方法、LL方法)) (田伟, 辛涛, 2012; 祝玉芳, 丁树良, 2009)。考虑到篇幅限制, 挑选线型条件来做比较(因在本研究中, 线型结构下的判准率较其他结构低, 而前人研究是线型条件下判准率更高)。与前人实验条件相同：被试总分服从正态分布、人数为5000、属性层次结构为线型(7题)、失误率分别为2%、5%、10%、15%, 各实验条件重复 30次, 结果见表23。

从表 23可以看出, 在与前人条件完全相同的情况下, 该方法的判准率表现出一定的优势, 尤其是在失误率增大的情况下, 该方法的模式判准率表现出了更好的稳定性, 然而其思路和方法却比前人方法简单, 因此该方法具有较强的适用性与稳定性,能够满足当前测验改革的实践情境, 实现对被试知识状态的准确分类与诊断。

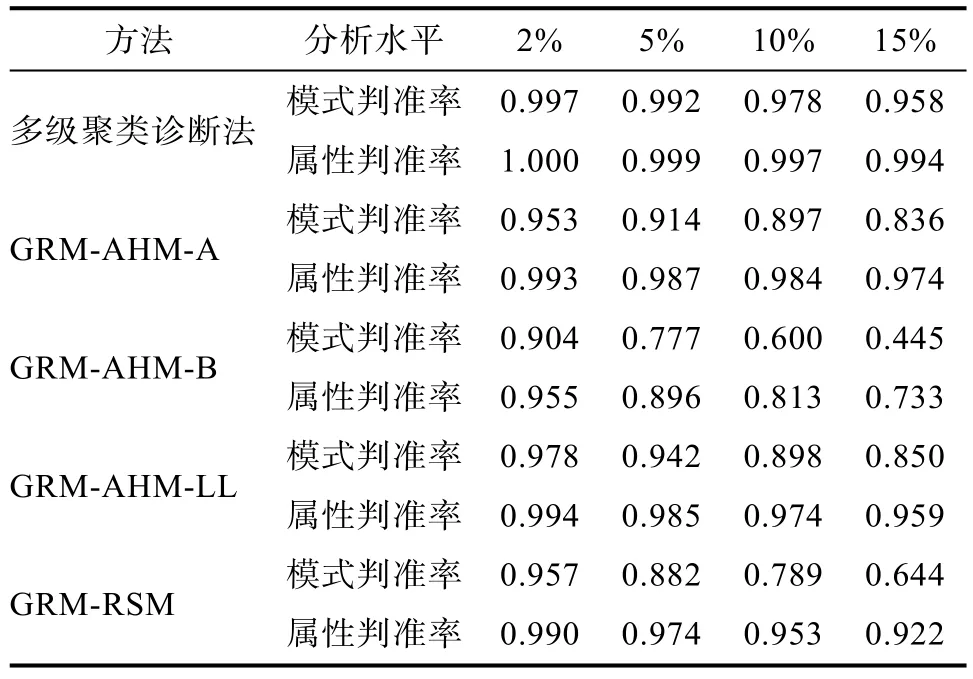
表23 GRCDM与前人方法的比较

6.2 GRCDM对样本容量的依赖性较小

以往研究发现, 被试容量和题目容量对 PMR的影响较大, 研究者比较了这两者对五大认知模型判准率的影响, 结果表明在100人/20题时, PMR值最高为 94.14%, 多数为73%左右, 最低才 34.75%,随着被试容量或题目容量的增加, 如在 100人/100题时或5000人/60题时, PMR得到明显改善(蔡艳,涂冬波, 丁树良, 2013)。因此, 要提高判准率, 要么增大被试容量, 要么增大题目容量。然而, 本研究中的被试容量最大为2000、其次为500和100, 题目容量最多为25题, 模拟研究发现, 失误率为5%和 10%时, 样本容量不存在主效应, 且与其它因素也不存在交互效应, 这表明样本容量的大小不会导致判准率的差异, 此时, 即使是100人, PMR和MMR在各层次结构中的最低值都达 94.9%。另外, 当失误率为 20%时, 也仅发散型和无结构型下, 表现为2000人、500人的PMR值显著高于100人, 其增幅最多也仅为7.82%, 500人与2000人差异并不显著。可见, 该方法具有不依赖样本容量的优势, 100人与500人的样本容量就能达到很高的判准率, 这为CDA走向小型测验及课堂评估奠定了一定的基础。

6.3 GRCDM对属性层级的紧密性依赖较小

以往研究表明, 层次结构对判准率影响较大,属性间逻辑关系越紧密, 判准率越高; 属性间逻辑关系越松散, 判准率偏低(蔡艳等, 2013; 田伟, 辛涛, 2012)。本研究中, 属性层次关系及其与样本容量的交互作用对 PMR会产生影响, 但其影响的方向和强度不同。模拟研究发现, GRCDM在各层次关系下的MMR和PMR均很高(发散型、线型、无结构型、收敛型的 PMR依次为：99%、94.55%、94.54%、93.33%)。当考虑失误率和样本容量时, 在5%和 10%失误率时, 发散型和无结构型(5%：99.98%、99.65%; 10%：99.76%、97.85%)下的PMR虽显著高于线型和收敛型(5%：97.96%、97.4%;10%：95.76%、94.74%), 但差异量最多仅为5.02%,且与样本容量无关; 当失误率增加到 20%时, 各样本容量下均为发散型表现最优(96.2%、97.35%、97.8%), 在小样本容量(100人和500人)时, 无结构型稍差(81.47%、87.70%)。由此可见, GRCDM在各层次结构下具有较好的稳健性, 在失误率不高的情况下, 尤其适用于发散型和无结构型, 且不受样本容量影响; 随着失误率的增加, 若样本容量能保持在500人以上, 该方法依然能保持较好的稳健性。

6.4 GRCDM在实践中具有良好的内外部效度

为考察GRCDM在实践中的适用性, 本研究对1240名学生在行程问题上的表现进行了评估。研究发现, 学生在 8个属性上的掌握比例较高的是 A1和A2, 居中的是A3、A6, 相对较低的是A4、A5、A7、A8。在这些属性中, A1、A2、A3测量的是基本计算、基本概念及多步运算, 作为高年级小学生理应较好的掌握; A5、A7和 A8为认知过程属性,属于认知技能, 本来难度就相对较大; A4虽为知识内容属性, 但掌握 A4需以掌握较多属性为前提,因此难度也较大。可见, GRCDM 所得各属性的难度趋势与属性性质、属性层次关系是相匹配的, 该方法具有较好的内部效度。利用学校类型作为外部校标, 对好中差学校学生的属性通过率进行差异分析表明该方法具有较好的外部效度。当然, 后续研究还需通过多种方式收集外部效度证据。

6.5 研究展望

本研究虽然得到了一些有意义的结果, 但仍有地方需进一步完善。首先, 模拟研究中所得结果是在知识状态为均匀分布时产生的, 尽管聚类分析法对原始数据的分布形态不作要求, 但被试知识状态的分布会不会影响其判准率, 需进一步探讨; 其次,在计算属性合分时, 基于被试在每道题上的得分推测其各属性的得分, 是采用属性等权重的思想, 即有可能是A2或A4得分时, 各取0.50, 而实际上属性难度会有不同, 如何基于属性的先验信息, 赋予不同属性不同权重, 是后续关于属性合分研究应考虑的问题; 最后, 后续还应关注GRCDM与其它参数或非参数方法的直接比较, 进一步考证其在诊断分类中的优越性, 以获得更为直接可靠的结论。

7 结论

本文通过模拟和实证研究探讨了 GRCDM 在CDA中的适用性, 得到以下结论：(1)该方法在 36种试验条件下均表现出较高的PMR和MMR;(2)该方法对样本容量依赖小, 可以适用于小型测评和课堂评估; (3)该方法在各属性层次结构下, 其判准率均较高, 特别是在发散型和无结构型下, 也能达到很高水平, 这为解决判准率受层次结构紧密度影响的困境找到了一个突破口; (4)GRCDM在实践情境中也同样表现出较好的内外部效度。

Ayers, E., Nugent, R., & Dean, N. (2008, June). Skill set profile clustering based on student capability vectors computed from online tutoring data. In R. S. J. d. Baker, T.Barnes, & J. E. Beck (Eds.), Educational data mining 2008:Proceedings of the 1st International Conference on Educational Data Mining (pp. 210–217). Retrieved from http://www.educationaldatamining.org/EDM2008/.

Borsboom, D., Mellenbergh, G. J., & van Heerden, J. (2004). The concept of validity. Psychological Review, 111(4), 1061–1071.

Cai, Y., Tu, D. B., & Ding, S. L. (2013). A simulation study to compare five cognitive diagnostic models. Acta Psychologica Sinica, 45(11), 1295–1304.

[蔡艳, 涂冬波, 丁树良. (2013). 五大认知诊断模型的诊断正确率比较及其影响因素: 基于分布形态, 属性数及样本容量的比较. 心理学报, 45(11), 1295–1304.]

Chiu, C.-Y., & Douglas, J. (2013). A nonparametric approach to cognitive diagnosis by proximity to ideal response patterns. Journal of Classification, 30(2), 225–250.

Chiu, C.-Y., Douglas, J. A., & Li, X. D. (2009). Cluster analysis for cognitive diagnosis: Theory and applications.Psychometrika, 74(4), 633–665.

De La Torre, J., & Douglas, J. A. (2004). Higher-order latent trait models for cognitive diagnosis. Psychometrika, 69(3),333–353.

Fu, J., & Li, Y. (2007). Cognitively diagnostic psychometric models: An integrative review. Paper presented at the annual meeting of the National Council on Measurement in Education, Chicago, IL.

Hartz, S. M. (2002). A Bayesian framework for the unified model for assessing cognitive abilities: Blending theory with practicality. 63, ProQuest Information & Learning, US.Retrieved from http://search.ebscohost.com/login.aspx?direct=true&db=ps yh&AN=2002-95016-234&lang=zh-cn&site=ehost-live Available from EBSCOhost psyh database.

Henson, R., Templin, J., & Douglas, J. (2007). Using efficient model based Sum-scores for conducting skills diagnoses.Journal of Educational Measurement, 44(4), 361–376.

Hu, Z. J. (Ed.). (2010). Psychological statistics. Beijing, China:Higher Education Press.

[胡竹菁. (2010). 心理统计学. 北京: 高等教育出版社.]

Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3), 258–272.

Kang, C. H. (2011). Cognitive diagnostic assessment on primary school students' arithmetic word problem solving (Unpublished doctorial dissertation). Beijing Normal University.

[康春花. (2011). 小学数学应用题问题解决的认知诊断研究(博士学位论文). 北京师范大学.]

Kang, C. H., Xin, T., & Tian, W. (2013). Development and validation of diagnostic test for primary school arithmetic word problems. Examinations Research, (6), 24–43.

[康春花, 辛涛, 田伟. (2013). 小学数学应用题认知诊断测验编制及效度验证. 考试研究, (6), 24–43.]

Kim, S., Walker, M. E., & McHale, F. (2010). Investigating the effectiveness of equating designs for constructed-response tests in large-scale assessments. Journal of Educational Measurement, 47(2), 186–201.

Leighton, J. P., Gierl, M. J., & Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka's Rule-space approach. Journal of Educational Measurement, 41(3), 205–237.

Luo, H., Ding, S. L., Wang, W. Y., Yu, X. F., & Cao, H. Y.(2010). Attribute hierarchy method based on graded response model with different scoring-weight for attributes.Acta Psychologica Sinica, 42(4), 528–538.

[罗欢, 丁树良, 汪文义, 喻晓锋, 曹慧媛. (2010). 属性不等权重的多级评分属性层级方法. 心理学报, 42(4), 528–538.]

Nugent, R., Ayers, E., & Dean, N. (2009, July). Conditional subspace clustering of skill mastery: Identifying skills that separate students. In T. Barnes, M. Desmarais, C. Romero,& S. Ventura (Eds.), Educational Data Mining 2009:Proceedings of the 2nd International Conference on Educational Data Mining (pp. 101–110). Retrieved from http://www.educationaldatamining.org/EDM2009/.

Tatsuoka, K. K. (1983). Rule space: An approach for dealing with misconceptions based on item response theory.Journal of Educational Measurement, 20(4), 345–354.

Tian, W., & Xin, T. (2012). A polytomous extension of rule space method based on graded response model. Acta Psychologica Sinica, 44(1), 249–262.[田伟, 辛涛. (2012). 基于等级反应模型的规则空间方法.心理学报, 44(1), 249–262.]

Tu, D. B., Cai, Y., Dai, H. Q., & Ding, S. L. (2010). A polytomous cognitive diagnosis model: P- DINA model.Acta Psychologica Sinica, 42(10), 1011–1020.

[涂冬波, 蔡艳, 戴海琦, 丁树良. (2010). 一种多级评分的认知诊断模型: P-DINA 模型的开发. 心理学报, 42(10),1011–1020.]

Zhu, Y. F., & Ding, S. L. (2009). A polytomous extension of attribute hierarchy method based on graded response model.Acta Psychologica Sinica, 41(3), 267–275.

[祝玉芳, 丁树良. (2009). 基于等级反应模型的属性层级方法. 心理学报, 41(3), 267–275.]