Search Space Pruning Based on Image Tools for Preliminary Inrerplanerary Trajecrory Design

Yang Dalin（杨大林），Xu Bo（徐波），Gao Youtao（高有涛）*

1.College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China；2.School of Astronomy&Space Science，Nanjing University，Nanjing 210093，P.R.China

（Received 13 October 2014；revised 10 March 2015；accepted 20 April 2015）

Search Space Pruning Based on Image Tools for Preliminary Inrerplanerary Trajecrory Design

Yang Dalin（杨大林）1，Xu Bo（徐波）2，Gao Youtao（高有涛）1*

1.College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China；2.School of Astronomy&Space Science，Nanjing University，Nanjing 210093，P.R.China

（Received 13 October 2014；revised 10 March 2015；accepted 20 April 2015）

Absrracr：A novel gravity assist space pruning（GASP）algorithm based on image tools is proposed for solving interplanetary trajectory optimization problem.Compared with traditional GASP algorithm，the concept of image is introduced to avoid missing interesting solutions with appropriate number of function evaluations.Image tools allow us to evaluate the objective function in regions in place of points and provide an effective way to evaluate the forward and backward constraints for the multi-gravity assist trajectory optimization problem.Since the interesting solutions of the interplanetary trajectory optimization problem are often clustered in a small portion of the search space rather than being overall evenly distributed，the regionwise evaluations with image tools make the little large interval with the proper Lipschitzian tolerances sampling effective.The detailed steps of the proposed method are presented and two examples including Earth Venus Mars（EVM）transfer and Earth Venus Venus Earth Jupiter Saturn（EVVEJS）transfer are given.Finally，a comparison with solutions given by the literature demonstrates the effectiveness of the proposed method.

trajectory optimization；global optimization；local minima；gravity assist space pruning（GASP）algorithm；image tool

0 Inrroducrion

Interplanetary trajectory design problem can be formalized as global optimization problem［1-2］. Multiple gravity assist（MGA）problem and multiple gravity assist with one deep space maneuver（MGA-1DSM）problem are essentially two optimization problems which describe a spacecraft equipped with a chemical propulsion system travelling in the solar system.The spacecraft is constrained to thrust only at planetary encounters in MGA problem.However，this limitation is removed in MGA-1DSM problem，and its engine is allowed to thrust once at any time during each trajectory leg.The objective of the trajectory optimization is to search trajectories for spacecraft that are optimal with respect to propellant consumption or transfer time.Consequently，more complex mission can be completed under the existing engineering constraints.

According to the type of the thruster considered for the spacecraft，the trajectory design and optimization problems can be divided into two main typologies.The first one is connected with spacecraft equipped with the chemical thruster，where the thrust duration is much shorter than the total flight time.Besides，the chemical thruster can achieve a high thrust.Therefore，it may be modeled as instantaneous velocity increment.The trajectory leg，as a reasonable first approximation，can be considered as the solution of two body problem.With the time nodes and the ephemeris for planets，the total magnitude of velocity increment can be determined.In mathematical，the trajectory optimization problem of spacecraft with chemical thruster is a finite di-mension global optimization problem with nonlinear constraints［3-6］.The second one appears with spacecraft equipped with a low but continuous thruster，which is applied to modify the trajectory of spacecraft over an extended period of time. The low thrust trajectory optimization problem is qualitatively different from the conventional chemical thruster situation，as the probe motion arc is not integral anymore.Moreover，magnitude and direction of the low thruster are constantly changing with time.The objective of low thrust trajectory optimization problem is to model and determine the optimal thrust vector so that the given performance index is optimized.Traditionally，low-thrust trajectory optimization problem are solved by the application of numerical optimal control theory.These methods are not the global optimal methods，and it is to find″a solution″not″the best solution″.The convergence behavior of these methods depends on a given initial guess，which is often hard to find［7-11］.

Because of the large time scale and the complicated relative motion between the planets，the landscape of the objective function presents a large number of clustered minima［12-13］，and it is easy to converge to one of local minima when using traditional optimizers.In addition，in order to avoid missing feasible solution，the initial scope of the search space is general relatively large［14］.Effective global optimization algorithms are encouraged and the research work is mainly divided into the following two classes.The first one is a problem of what appears to be a″blackbox″problem，some standard global optimization solvers，such as differential evolution（DE），particle swarm optimization（PSO），genetic algorithm（GA）and simulated annealing（SA），are introduced to solve the above problem.These solvers are not effective when used alone.However，the cooperative version can find a better solution in space trajectory optimization problem［1，15］.Besides the stochastic or heuristic methods list above，some deterministic methods like branching，branch and bound and the hybridization of stochastic and deterministic are proposed［16-18］.Some of them perform well in the specific problem and can identify the known best solutions in the corresponding problem.The second one appears with the structure of the search space and the nature of the problem are analyzed and may therefore be used to define the global optimization strategies.The efficiency has been demonstrated by the gravity-assist space pruning（GASP）algorithm，which is proposed by Myatt et al［19］.However，it was only used to preprocess the search space and some stochastic solvers are still used to search the reduced domains. Although the performance is better than the situation that the entire search space is managed by the stochastic solver directly，some isolated interesting solutions may still be left off.Thanks to the image tools，the boundary coordinates of the reduced domain distributed over the initial search space can be identified easily by the matlab toolbox.A novel method which blends the characteristics of GASP algorithm with the image identification，now called GASP-II algorithm，is proposed in this paper.

Besides，a method which blends the grid sampling with the image identification，now called GS-II algorithm，is also presented.GS-II is a method to substitute the stochastic solvers for searching the reduced domains.Grid sampling is an effective optimizer for low dimensionalities，but in high dimensionalities it is usually inefficient for large computational burden.In classical grid sampling process，the interval must be sufficiently fine to avoid loosing interesting domains. In this paper，grid sampling process will be divided into several steps until the global optimum is located.Firstly，the large interval with the large Lipschitzian tolerances are applied to avoid loosing interesting domains with little function evaluations.Then the grid sampling with appropriate interval is employed in the reduced domains obtained in the previous step.With the help of image identification，the boundary coordinates of the reduced domain can be identified easily.Repeat the previous step until the reduced domain is small enough to locate the global optimum effi-ciently.The Lipschitzian tolerances used to determine the reduced domain are always difficult to give，because the feasible domain may be left off with the inaccurate estimations.In this paper，the optimal solution in the previous grip sampling process is used as the Lipschitzian tolerance in next step which is demonstrated to be effective in next section.

1 Marhemarical Formalizarion

The interplanetary trajectories will be modeled by using the patched conic method.The fundamental assumption underneath this method is that the trajectory outside the scope of influence（SOI）of planets is the Kepler orbit around the sun.When the spacecraft is inside SOI of planets，the trajectories are the Keper orbit around the planet.Because of the large spatial scale of the solar system，the size of SOI can be ignored and simplified into a point in space for interplanetary trajectory.Each conic leg for interplanetary trajectories is the solution of Newton＇s law of universal gravitation

where r is the position of spacecraft andμthe gravitational constant of center body.Based on the above assumptions，the solution of the MGA problem represents an interplanetary trajectory of the spacecraft equipped with chemical rocket engines，and the engines are constrained to thrust only at planetary encounters［20］.In this paper，one considers the spacecraft launching from the Earth and finally reaching the target planet with the help of the gravitational pull of the planets the spacecraft flyby.The departure time from the Earth is t0，and the duration needed for each conic leg connecting two consecutive planets are Ti（i= 1，…，N+1），where N is the number of planets in the gravity assist sequence.Depending on the patched conic approximation，the heliocentric position vector of planetment and the heliocentric position vector of planetTjmoment can be given by the ephemeris，then the corresponding″Lambert problem″can be solved to give the departure velocity and the arrive velocity of each trajectory leg［21］.In order to simplify the description of the MGA problem，multiple revolution cases and retrograde cases are not considered in this paper. After that，the powered flyby trajectories are determined by the entrance velocityand the exit velocitywhich are given by the above″Lambert problem″［22］.The details are shown in Fig.1.

Fig.1 Illustration of geometric definition of MGA problem

In general，a problem statement for interplanetary trajectory optimization can be stated as follows

Performance index

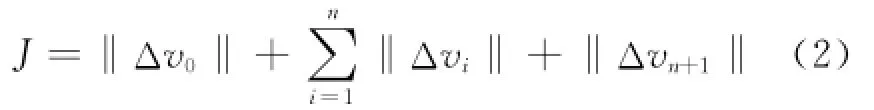
whereΔv0is the velocity increment corresponding to the Earth departure phase，Δvi（i=1，…，n）the velocity increment corresponding to the powered flyby phase，andΔvn+1the braking maneuver in the final rendezvous phase.

Boundary condition

whereτ=［t0，T1，…，TN+1］and I⊆RN+2.

Phase matching conditions

where Ri（i=1，…，N+1）and r are the heliocentric position of planets and spacecraft andstarting epoch and the final epoch corresponding to the phase i，respectively.

Nonlinear constraints

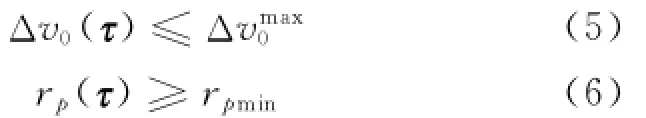
2 Preliminary Analysis

This section analyzes the difficulty of solving the interplanetary trajectory design problem from a global optimization standpoint.The objective function is the total velocity increment the spacecraft required to reach the target planet，and the decision variables include the departure time t0and the transfer time Ticorresponding to each leg.In order to present the structure of the search space completely，several synodic periods will be required in the bounds of the decision variables. Here，the structure of the search space is given by a simple problem，for example the Earth-Mars transfer.The underlying geometry of the objective function corresponding to the Earth-Mars transfer in the 2D search space is shown in Fig.2.

Fig.2 Objective function landscape of Earth-Mars transfer in 2D search space

In Fig.2，it indicates that several local minima are present in search space，and the objective function is quasi-periodic in nature due to the synodic period of planets.Once considering gravity assist maneuver，which is an effective way to reduce the fuel consumption at the cost of increasing mission duration for an intended mission，it will result in a high dimensional optimization problem，which cannot be solved by deterministic methods efficiently.Myatt et al.［19］proposed a pruning strategy named gravity assist space pruning（GASP）algorithm.The main idea of the GASP algorithm is that high dimensionalities in the MGA problem can be spitted into a series of two dimensional optimization problems where deterministic methods like grid sampling are computationally efficient.After that，the back-ward and forward pruning criteria based on physical and technological constraints of an interplanetary trajectory are applied to reduce the search space. The output of the GASP algorithm is a series of hyperrectangles where the optimal solutions are contained.The GASP algorithm improves the performances of optimization tools compared with the traditional optimization phase where the optimization tools are used to search the original search space directly.

3 Search Space Pruning Based on Image Tools

As mentioned above，there are a large number of clustered minima exist in the interplanetary trajectory optimization problem.In order to find interesting solutions，extensive work has been devoted to the global interplanetary trajectory optimization problem.Inspired by the basic idea of the GASP algorithm that a high dimensional trajectory optimization problem can be reduced into a series of two dimensional optimization problems，we find that the objective function in the MGA problem is constituted of several orbit maneuver corresponding to different mission phases.Different from the GASP algorithm，the orbit maneuver at the Earth departure segment and target planet arrival segment are determined by the two dimensional optimization problems and the orbit maneuver at mid-planetary encounters are determined by the three dimensional optimization problem instead of double two dimensional optimization problem.With the help of image tools，the structure of solution obtained in three dimensional optimization problem can be projected into each 2D search space.Utilization the basic idea mentioned above with the motivation that interesting solutions of interplanetary trajectory optimization problem are often clustered in a smallportion of the search space rather than being evenly distributed all over it，the GASP-II algorithm and the GS-II algorithm are proposed in this paper.

Consider once again the objective function in the MGA problem，and introduce the map

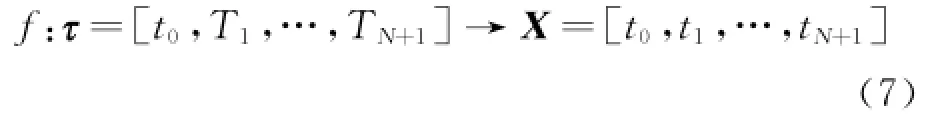
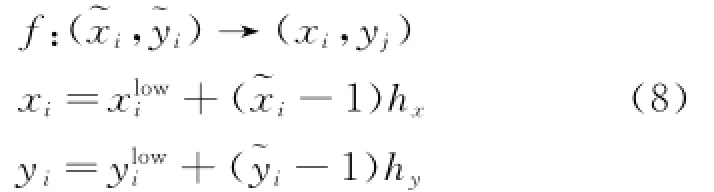
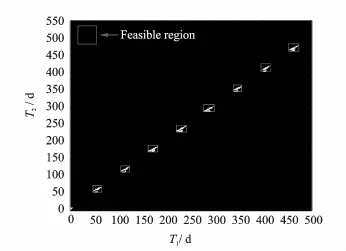
Fig.3 Feasible region corresponding to the first two components of decision vector

Considering the powered gravity assist process in the MGA problem，the velocity increment required during the powered gravity process can be determined by the entrance and exit excess velocities of the spacecraft relative to the flyby planet.With reference to Fig.1，we consider the first powered gravity assist maneuver.The entrance excess velocityare known from（t0，t1），the exit excess velocityare known from（t1， t2），which meansΔv1=f（t0，t1，t2）.Once t0，t1，t2are given，the velocity increment and the pericenter radius of the planetocentric trajectory are determined.Applying the maximum gravity assist thrust constraint and minimum pericenter radius constraint（the periapse of gravity assist trajectory under the minimum safe distance）can prune out the infeasible regions from the cube search space（t0，t1，t2）.In order to get the boundary coordinates of the smallest cube containing the feasible regions，the cube feasible regions are projected to（t0，t1）plane and（t1，t2）plane，respectively.Then the image tools are used to identify the boundary coordinates，which are shown in Figs.4，5.The regions pruned out based on the maximum allowingΔv at departure turn out to be the unfeasible regions for the first powered gravity assist，similar criterions for the following processing；Then constraints in the MGA problems can be propagated forward and backward and the search space can be pruned step by step.Consequently，it can significantly reduce the burden of computer to locate the optimum solutions.

As well as the maximum allowingΔv at departure，it is ordinary to consider the constraint on the maximum allowed braking maneuver the spacecraft can perform.When the spacecraft arrives at the target planet，the hyperbolic excess velocity relative to the target planetΔvn+1only depends on the last segment of interplanetary trajectory，which means the last two components in decision vector（tN×tN+1）.Applying the maximum allowableΔvn+1constraint can prune out the infeasible regions from（tN×tN+1）search space，which is shown in Fig.6.After that，the boundary of feasible region can be further narrowed according to the forward and backward constraints.Final-ly，the reduced search space，consisted of the feasible regions according to the physical and technological constraints in the interplanetary mission，is described clearly with the help of image tools. There are usually several feasible regions distributed in the search space，and parallel computer is introduced to search the feasible regions at the same time，which can greatly shorten the time required to locate the optimum solutions.

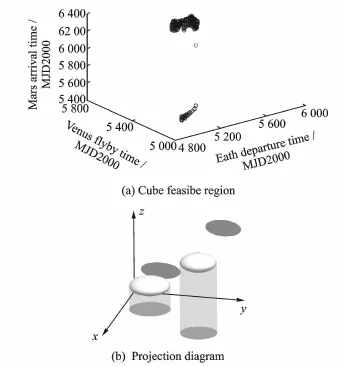
Fig.4 Cube feasible region pruned by venus flyby constraints

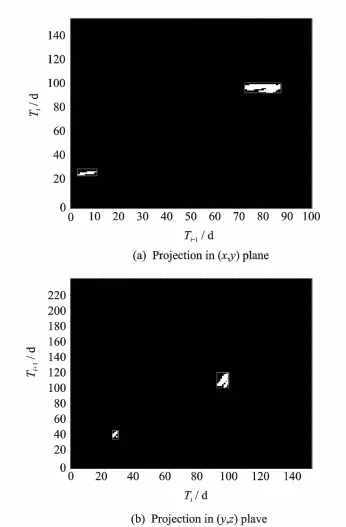
Fig.5 Projection of cube feasible region into plane

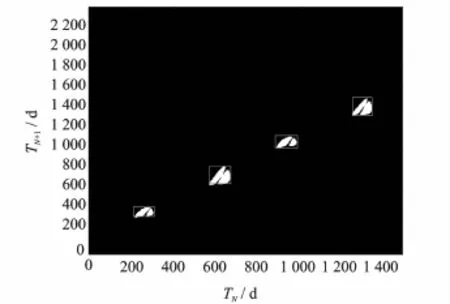
Fig.6 Feasible region corresponding to the last two components of decision vector

Traditionally，the reduced search space is searched by optimization tools such as DE algorithm，GA，SA algorithm，and PSO algorithm. However，the solution cannot still be guaranteed to a global optimum.In this paper，the GS-II algorithm is proposed to locate the optimum solutions in reduced search space，which will be described in detail in the Earth-Mars example. Therefore，the input of the GASP-II algorithm is the initial bounds of decision vector and planets sequence.The output is the hyperrectangles feasible regions containing the optimal solution.The input of the GS-II algorithm is the hyperrectangles feasible regions given by the GASP-II algorithm，and the output is the optimal solution.

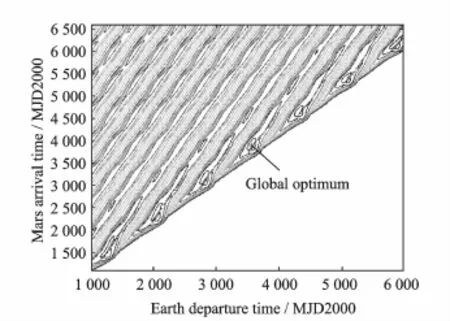
Fig.7 Objective function landscape of Earth-Mars transfer

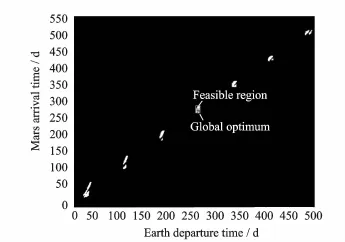
Fig.8 Feasible region given by image processing version of GASP algorithm

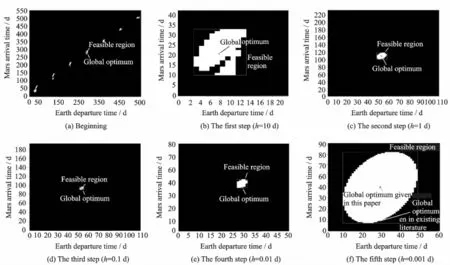
Fig.9 Process of image processing version of grid sampling algorithm

Table 1 Search space for Earrh-Mars rransfer

In order to demonstrate the effectiveness of the proposed method in this paper，the Earth-Mars transfer is addressed.This is because the search space is intuitive and the location of the global optimum is certain（Fig.7）.The initial bounds of search space are given in Table 1.The GASP-II algorithmstated above is carried out，and the reduced search space is shown in Fig.8. Then the GS-II algorithm is applied to handle the reduced search space.Grid sampling algorithm is an effective optimizer for low dimensionalities. The interval must keep sufficiently fine to avoid loosing interesting solutions，while the small interval will make the number of function evaluations increase steeply.For the interesting solutions are often clustered in a small portion of the search space，the large interval with the large Lipschitzian tolerances are applied at the beginningto avoid loosing interesting solutions with little number of function evaluations.Then the grid sampling with appropriate interval is employed in the reduced domains，which are obtained in previous step.Thanks to the image tools，the boundary coordinates of the reduced domain can be identified easily.Repeat the previous step until the reduced domains is small enough to make the grid sampling algorithm to locate the global optimum efficiently.The whole process of the application of the GS-II algorithm is shown in Fig.9 and Table 2.The computational time in each step are also given in Table 2 to represent a proof of theefficiency and the time is relative to a PC，1.9 GHzCPU，512 MB RAM.Numerical simulation results show that the objective functions of the solutions contains in the feasible region in last step are better than that of the global optimum solution given in existing literature，and the visualization of best solution of Earth-Mars transfer is shown in Fig.10.

Table 2 Reduced search space and besr idenrified solurion for Earrh-Mars rransfer

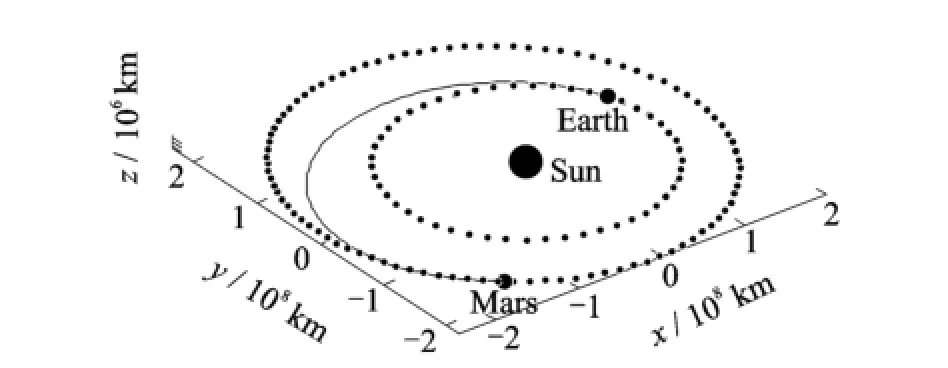
Fig.10 Projection into ecliptic plane of Earth-Mars transfer

4 Simularion Resulrs

In order to demonstrate the effectiveness of the proposed algorithm in high dimensionalities，some relevant simulation studies are addressed and some results given by the methodology proposed in this paper are compared with existing literature.

4.1 Earrh Venus Mars

Considering the spacecraft departing from Earth，and flying to Mars with the help of the gravitational pull of Venus.Deep space maneuver（DSM）is constrained only at Venus encounters. This situation can formalized as MGA trajectory optimization problem，whereas the decision vector isτ=［t0，t1，t2］，and the objective function evaluated in the process of the methodology proposed in this paper is shown as follows

whereΔv0is the velocity increment corresponding to the Earth departure phase，Δv1the velocity increment corresponding to DSM at Venus encounters，andΔv2the velocity increment at the Mars arrival.The initial bounds of search space are given in Table 3.

Table 3 Search space for rransfer

The threshold values of space pruning are given 5 km/s at the Earth departure，5 km/s at the Mars arrival，and 2 km/s at the Venus powered flyby.The feasible regions are automatically saved and identified by using the image processing version of the GASP algorithm.The associated parameters are given Table 4.After that，image processing version of grid sampling algorithm is applied to locate the interesting solutions iteratively.The performances with respect to transfer time and total velocity increment are given in Table 4，including comparisons to that obtained by Armellin et al［23］.The projection into the ecliptic plane of Earth Venus Mars（EVM）transfer corresponding to the best solution is visualized in Fig.11.

Table 4 Reduced search space and besr idenrified solurion for EVM rransfer

Fig.11 Projection into ecliptic plane of EVM transfer

4.2 Earh Venus Venus Earrh Jupirer Sarurn

This is a particular instance of the MGA problem［24］，which is related to the Cassini spacecraft transfer trajectory optimization problem. The spacecraft depart from the Earth and fly to Saturn via multiple gravity assist.Finally，the spacecraft will be captured by the gravity field of Saturn.The pericenter radius is 108 950 km，the eccentricity is 0.98.The sequence considered here is Earth Venus Venus Earth Jupiter Saturn（EVVEJS），which is similar to that used by Cassini spacecraft.The initial bounds of the six dimensional decision vector are given in Table 5. The objective function used is the total velocity increment

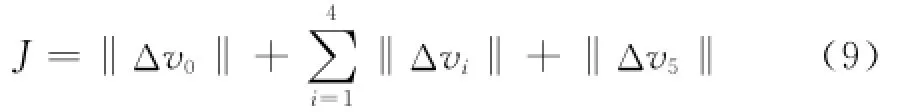
whereΔv0is the velocity increment corresponding to the Earth departure phase，Δvithe velocity in-crement the required at the planets powered flyby，andΔv5the velocity increment at Saturn arrival.

Table 5 Search space for EVVEJS rransfer

The threshold values of space pruning are 5 km/s at the Earth departure，2 km/s at the Saturn arrival and 2 km/s at Planets powered flyby.With the increase of dimension，the complexity of solving the MGA problem increases rapidly.There are a lot of feasible regions reserved in the 1st step.Due to the limit space，partial feasible region are listed in Table 6.The performances with respect to transfer time and total velocity increment are also given in Table 6.Finally，a comparison with the solutions given by existing literature is given in Table 7［25］.The projection into the ecliptic plane of EVVEJS transfer corresponding to the best solution is visualized in Fig.12，where Fig.12（b）is large from the central part in Fig.12（a）.

Fig.12 Projection into ecliptic plane of EVVEJS transfer

Table 6 Reduced search space and besr idenrified solurion for EVVEJS rransfer

Table 7 Trajecrory design resulrs

5 Conclusions

From the view of global optimization，interplanetary trajectory optimization problem can be formalized as the MGA problem.Numerous local minimum values exist in the interplanetary trajectory optimization problem due to the complicated relative motion between the planets.With the help of image tools，the structure of search space become intuitive，and the infeasible regions can be pruned effectively according to the forward and backward constraints.Grid sampling is usually inefficient in high dimensionalities，but for the clustered interesting solutions in reduced search space，the large interval with the large Lipschitzian tolerances can locate the feasible regions with the appropriate number of function evaluations. After that，the Lipschitzian tolerances are reduced step by step.The effectiveness of the methodology proposed in this paper is demonstrated by the Earth-Mars transfer and the test problems with the characteristic of high dimensionalities.

Acknowledgemenrs

This work was supported by the National High Technology Research and Development Program（863）of China（2012AA121602），the National Natural Science Foundation of China（11078001），the Specialized Research Fund for the Doctoral Program of Higher Education of China（20133218120037），and the Fundamental Research Funds for the Central Universities under Grant（NS2014091）.

［1］ Vinko T，Izzo D.Global optimisation heuristics and test problems for preliminary spacecraft trajectory design［R］.ESA 231-238.European Space Agency：Advanced Concepts Team，2008.

［2］ Vasile M，Pascale P D.Preliminary design of multiple gravity assist trajectories［J］.Journal of Spacecraft and Rockets，2006，43（4）：794-805.

［3］ Battin R H.An introduction to the mathematics and methods of astrodynamics［M］.Washington：AIAA，1999：47-58.

［4］ Addis B，Cassioli C，Locatelli M，et al.A global optimization for the design of space trajectories［J］. Computational Optimization and Applications，2011，48（3）：635-652.

［5］ Bessette C R，Spencer D B.Identifying optimal interplanetary trajectories through a genetic approach［C］//Astrodynamics Specialist Conference and Exhibit.Keystone：AIAA，2006：437-448.

［6］ Bessette C R，Spencer D B.Optimal space trajectory design：A heuristic-based approach［J］.Advances in the Astronautical Sciences，2006，124：1611-1628.

［7］ Betts T.Practical methods for optimal control and estimation using nonlinear programming［M］.Washington：The Boeing Company，2001：191-204.

［8］ Betts J T.Survey of numerical methods for trajectory optimization［J］.Journal of Guidance，Control and Dynamics，1998，21（2）：193-207.

［9］ Petropoulos A E，Longuski J M.Shape based algorithm for the automated design of low thrust，gravity assist trajectories［J］.Journal of Spacecraft and Rockets，2004，41（5）：787-796.

［10］Schütze O，Vasile M，Junge O，et al.Designing optimal low-thrust gravity-assist trajectories using space pruning and a multi-objective approach［J］. Engineering Optimization，2009，41（2）：155-181.

［11］Shen H X，Zhou J P，Peng Q B，et al.Multi-objective interplanetary trajectory optimization combining low thrust propulsion and gravity assist maneuvers［J］.Science China Technological Sciences，2012，55（3）：841-847.

［12］Vasile M.A systematic-heuristic approach for space trajectory design［J］.Annals of the New York Academy of Sciences，2004，1017（1）：234-254.

［13］VinkóT，Izzo D，Bombardelli C.Benchmarking different global optimisation techniques for preliminary space trajectory design［C］//58th International Astronautical Congress.Hyderabad：IAF，2007：189-199.

［14］Yang D L，Xu B，Lei H L.Multi-objective detection trajectory optimization design in solar system［C］// 64th International Astronautical Congress.Beijing：IAF，2013：635-652.

［15］Vasile M，Locatelli M.A hybrid multiagent approach for global trajectory optimization［J］.Journal of Global Optimization，2009，44（4）：461-479.

［16］Jones D R，Perttunen C D，Stuckman B E.Lipschitzian optimization without the Lipschitz constant［J］. Journal of Optimization Theory and Applications，1993，79（1）：157-181.

［17］Horn M.Optimal algorithms for global optimization in case of unknown Lipschitz constant［J］.Journal of Complexity，2006，22（1）：50-70.

［18］Vasile M，Summerer L，de Pascale P.design of Earth-Mars transfer trajectories using evolutionarybranching technique［J］.Acta Astronautica，2005，56（8）：705-720.

［19］Izzo V M，Myatt D，Nasuto D R.Search space pruning and global optimisation of multiple gravity assist spacecraft trajectories［J］.Journal of Global Optimization，2007，38（2）：283-296.

［20］Bruce A.Spacecraft trajectory optimization［M］. Cambridge，UK：Cambridge University，2010：756-797.

［21］Arnett D，Meakin C，Young P A.The lambert problem［C］//Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis.Barnes：ASP，2005：336-235.

［22］Labunskij A V，Papkov O V，Sukhanov K G.Multiple gravity assist interplanetary trajectories［M］. Florida：CRC Press，1998：1147-1152.

［23］Armellin R，Di Lizia P，Topputo F，et al.Gravity assist space pruning based on differential algebra［J］. Celestial Mechanics and Dynamical Astronomy，2010，106（1）：1-24.

［24］Peralta F，Flanagan S.Cassini interplanetary trajectory mission［J］.Control Engineering Practice，1995，11（3）：1603-1610.

［25］Izzo D.GTOP database-MGA problem-″Cassini″［P/ OL］（2005-12-08）［2014-08-12］.http：//www.esa. int/gsp/ACT/inf/op/globopt/evvejs.htm.

（Executive Editor：Xu Chengting）

V412Documenr code：AArricle ID：1005-1120（2015）05-0530-11

*Corresponding aurhor：Gao Youtao，Lecturer，E-mail：ytgao@nuaa.edu.cn.

How ro cire rhis arricle：Yang Dalin，Xu Bo，Gao Youtao.Search space pruning based on image tools for preliminary interplanetary trajectory design［J］.Trans.Nanjing U.Aero.Astro.，2015，32（5）：530-540.

http：//dx.doi.org/10.16356/j.1005-1120.2015.05.530