基于改进LMD方法的故障转子振动分析*

邓林峰，赵荣珍，靳伍银（兰州理工大学机电工程学院 兰州，730050）

基于改进LMD方法的故障转子振动分析*

邓林峰，赵荣珍，靳伍银
（兰州理工大学机电工程学院 兰州，730050）

针对二次样条插值（cubicsplineinterpolation，简称CSI）局部均值分解（localmeandecomposition，简称LMD）方法在处理故障振动信号时准确性较低的缺陷，提出了一种集成自适应波形匹配、二次B样条插值（cubicB-splineinterpolation，简称CBI）以及正交性判据（orthogonalitycriterion，简称OC）的LMD改进方法。首先，利用自适应波形匹配技术对原始信号进行数据延拓；然后，采用CBI代替CSI求解信号的上、下包络线，进而求得局部均值函数和包络估计函数；最后，以OC作为乘积函数（productfunction，简称PF）内部迭代过程结束的判断条件，形成一种改进的CBI-LMD方法。仿真分析与实验验证的结果表明，该改进方法具有更好的信号分解性能，能够准确有效地提取出复杂非平稳信号的重要特征。

局部均值分解；二次B样条插值；正交性判据；故障转子；振动分析

引 言

通过分析振动信号对旋转机械进行状态监测和故障诊断是最有效、最常用的方式［1］。然而，由于故障发生时的振动信号往往表现出非平稳的特性，使得振动信号的分析变得十分困难［2］。局部均值分解是由Smith为更准确地分析处理调幅-调频信号而提出的一种自适应的非平稳信号分析方法，并将其成功地应用于脑电信号的分析处理过程中［3］。LMD与经验模态分解（empiricalmodedecomposition，简称EMD）十分相似，二者都可以将一个包含多成分的复杂信号分解为若干个具有物理意义的单分量信号。与EMD相比，LMD不存在过、欠包络和边界效应等问题，且LMD不需要构造解析信号再经过Hilbert变换才能计算瞬时特征，而是在分解信号的过程中，LMD方法就计算出了相应的瞬时幅值和瞬时频率。因此，LMD比EMD具有更高的计算效率。LMD方法的这些优势引起了科研人员的普遍关注，并迅速成为故障诊断领域分析非平稳振动信号的一个研究热点［4-6］。

目前，LMD方法在机械故障诊断中的应用研究的重点是：利用LMD或其改进方法从振动信号当中提取故障特征以描述故障状态，或者将LMD与其他智能计算以及分类方法相结合，进行故障的智能模式辨识［7-10］。这些研究不仅提升了故障诊断技术自身的水平，而且推动了各种智能计算方法在解决工程实标问题中的应用进程。其中，文献［7］将二次样条插值过程引入LMD，用于计算局部均值函数和包络估计函数，使LMD算法的计算效率和精度都有了一定的提升。但是，二次样条插值引起的过包络和欠包络问题也被引入到LMD中，使得信号分解的结果以及瞬时特征又会产生一些误差［7］。

由于B样条函数具有优良的局部性质，因此B样条插值可以避免过包络和欠包络问题，可保证计算结果具有较高的准确度。它已被成功地用于改进EMD，并形成了一种新的B样条EMD方法［11］，不仅避免了EMD的过包络和欠包络问题，而且提高了计算效率。基于此，笔者通过集成B样条插值、正交性判据以及自适应波形匹配技术，对CSI-LMD方法进行二次改进，以降低信号分解误差，进一步提高该方法分解非平稳信号的准确性。

1 基于样条捅值的LMD方法

原始的LMD方法中计算局部均值函数和局部包络函数的过程是由滑动平均算法完成的，然而该算法使得LMD在分解非平稳信号时存在分解精度和分解效率偏低的缺陷。为解决此问题，文献［7］将二次样条插值引入到LMD中，即用插值方法替换滑动平均算法来计算局部均值函数和局部包络函数，从而提高LMD算法分解信号的性能。经此过程改进后的样条插值算法的主要步骤如下。

1）对于任何信号x（t），搜索到它的所有局部极值点后，用极大值和极小值分别进行二次样条插值，形成上包络线Eu（t）和下包络线El（t）。

2）局部均值函数m（t）和局部包络函数a（t）可以用下式计算得到

3）接下来的步骤按照LMD算法的原过程步骤进行即可。

经过上述方式改进后的LMD算法称之为基于二次样条插值的LMD（简称CSI-LMD）方法。CSILMD方法是一个仅有两层循环结构的迭代过程，即改进的CSI-LMD算法比LMD算法少了一层计算两个局部函数的循环迭代过程，简化了LMD的算法结构，有利于提升LMD算法的性能。

尽管CSI-LMD算法的分解精度和效率相比LMD算法的分解精度和效率都有所提高，但是利用二次样条插值形成上、下包络线，不可避免地存在过包络和欠包络的问题，这使得由式（1）和式（2）计算的局部均值函数和局部包络函数也产生偏差，对最终的分解结果造成影响。若想消除CSI-LMD方法的这一缺陷，则需要借助一种具有更好局部特性的插值方法对其进行二次改进。

2 B样条捅值方法

为第k段n次B样条曲线段（k=0，1，…，m）。这些曲线段的全体称为n次B样条曲线；顶点Pi（i=0，1，…，m+n）又称为控制点；由这些控制顶点所组成的多边折线称为B样条曲线的特征多边形。

式（3）中的Gi，n（t）为n次B样条基函数，定义为

给定平面上的m+n+1个顶点Pi（i=0，1，…，m+n），称n次参数曲线段

其中：i=0，1，…，n。

大多数情况下取n=3，即采用二次B样条对控制点进行拟合。由式（3）可知，构造二次B样条曲线段只需要4个控制点，将构造的m+1段二次B样条曲线段连接起来即可形成完整的二次B样条曲线。

当n=3时，二次B样条曲线的基函数为

设4个控制点为Pi（i=0，1，2，3），则由式（3）可得二次B样条曲线为

其中：t为节点参数值。

由于B样条曲线并不通过控制点，因此对于给定的一组型值点Ri（i=0，1，…，h），首先，需要通过一种参数化方法求解节点矢量t=［t0，t1，…，th+2n］（两端点的重复度取n+1），本研究采用积累弦长参数化方法计算二次（n=3）B样条曲线的节点矢量；然后，利用文献［12］中的方法即可求出h+2个控制点；最后，将节点矢量和控制点代入式（6），得到通过型值点列的二次B样条插值曲线。

由于B样条曲线不仅保留了Bézier曲线的所有优点，而且二次B样条曲线在连接处保持二阶连续，所以它具有足够的光滑性。与二次样条插值相比，二次B样条插值具有变差缩减性以及更好的局部特性［12］，故本研究拟采用精度更高的CBI对CSILMD算法进行二次改进以提高其分解信号的性能。

3 CBI-LMD改进方法

基于以上描述，本研究提出CBI-LMD方法，其主要算法步骤如下。

1）找到任意信号x（t）的所有局部极值，用极大值作为型值点进行B样条插值，形成上包络线Eu（t）；用极小值作为型值点进行B样条插值，形成下包络线El（t）。

2）局部均值函数m（t）和局部包络函数a（t）可以通过式（1）和式（2）计算得到。

3）接下来的步骤按照LMD算法的原过程步骤进行即可。

与CSI-LMD方法相比，虽然CBI-LMD方法减弱了过、欠包络问题，但是在对信号进行分解的过程中产生一个PF分量的迭代终止条件，采用的仍然是局部包络函数的幅值要小于给定的阈值。这种固定的判别方式同样会使分解结果产生误差，并影响计算效率。另一方面，由文献［8］可知，一个信号x（t）的每个PF分量都满足

其中：k为PF分量的个数；T为信号长度。

式（7）说明每个PF分量都与将其从原始信号x（t）中分离出来的剩余部分近似正交。

对于每个PF分量而言，都应该满足式（7），只不过是不等号两边误差大小的问题。显然，不等号左边的值越接近于零，说明PF分量的正交性越好，LMD的分解结果就越准确。然而，利用LMD对实标信号进行分解时总会产生一定误差，从而影响了PF分量的正交性，最终导致分解结果及式（7）的误差偏大。

基于PF分量的上述特性，将正交性判据引入到CBI-LMD方法中，使其能够更准确有效地分析处理非平稳信号。正交性判据的定义［8］为

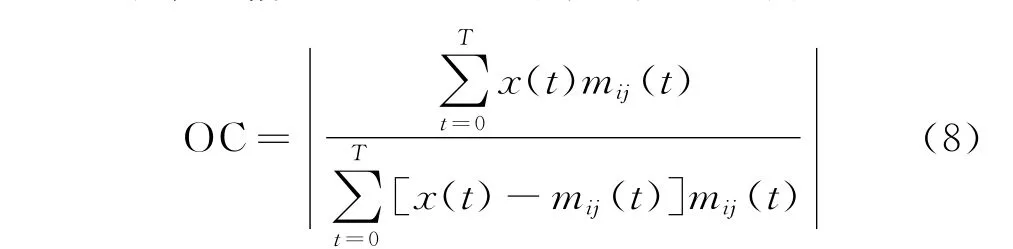
其中：x（t）为原始信号；mij（t）为LMD在求解第i 个PF分量时计算的第j次局部均值函数。

由于式（8）是基于式（7）而建立起来的，因此它能够很好地反映PF分量之间的正交性。此外，由LMD的分解步骤可知，随着迭代次数j不断增加，mij（x）将趋向于0，从而式（8）中的分子和分母将同时趋向于0，并且二者的收敛速度一致，即分子和分母是等价无穷小，所以OC的值将趋向于1，这与LMD方法理论上的迭代终止条件是一致的。可见，利用OC作为PF分量迭代终止的判断条件是完全可行的。但是，OC的值也只是趋近于1，并且存在一个最小值，为便于算法的具体判断，以前后两次迭代过程中OC的差值是否小于0做为迭代过程是否结束的判别条件。这不仅可以保证PF分量之间的正交性，而且能够减少分解过程的迭代次数和时间，从而提高算法的收敛速度。

由于B样条具有局部支撑性，而实标信号的端点与控制点之间又存在一定的跨度，因此会导致插值曲线出现严重的端点效应，从而降低了分解和计算结果的准确性［13］。为消除这一缺陷，笔者先通过自适应波形匹配方法对原始数据进行延拓，然后再进行基于OC的CBI-LMD分解过程。

对CSI-LMD方法进行以上3个方面的改进后，就形成基于数据延拓和OC的CBI-LMD方法，其算法流程如图1所示。为方便描述，仍以CBILMD表示基于数据延拓和OC的CBI-LMD方法。

图1中，CBI-LMD方法是一个仅具有两层循环结构的迭代过程，比原始LMD方法少了一层循环。CBI-LMD与CSI-LMD的主要区别就在于求包络线的插值方法和PF分量内部迭代过程的判据不同，这也正是CBI-LMD性能更好的主要原因。

图1 CBI-LMD算法流程图Fig.1 Flowchart of CBI-LMD

4 仿真分析和实验验证

为了验证本研究改进方法的有效性，分别利用仿真信号和转子实验信号对CSI-LMD与CBILMD方法的性能进行分析比较。

4.1 仿真分析

构造一个仿真信号x（t）为

其中：x1（t）是以60 Hz为中心频率的调幅-调频信号；x2（t）是频率为10 Hz的正弦信号。

式（9）是由两个不同的单分量信号组成的一个非平稳信号，其时域波形如图2所示。

图2 仿真信号Fig.2 A simulated signal

采用CSI-LMD和CBI-LMD方法对x（t）分别进行处理。对于CSI-LMD方法，纯调频信号的迭代终止条件设定为max［|1-ai（t）|］=0.01。x（t）经两种方法分解后的结果如图3所示。图4，5则分别给出了图3中两个PF1分量的瞬时幅值和瞬时频率。

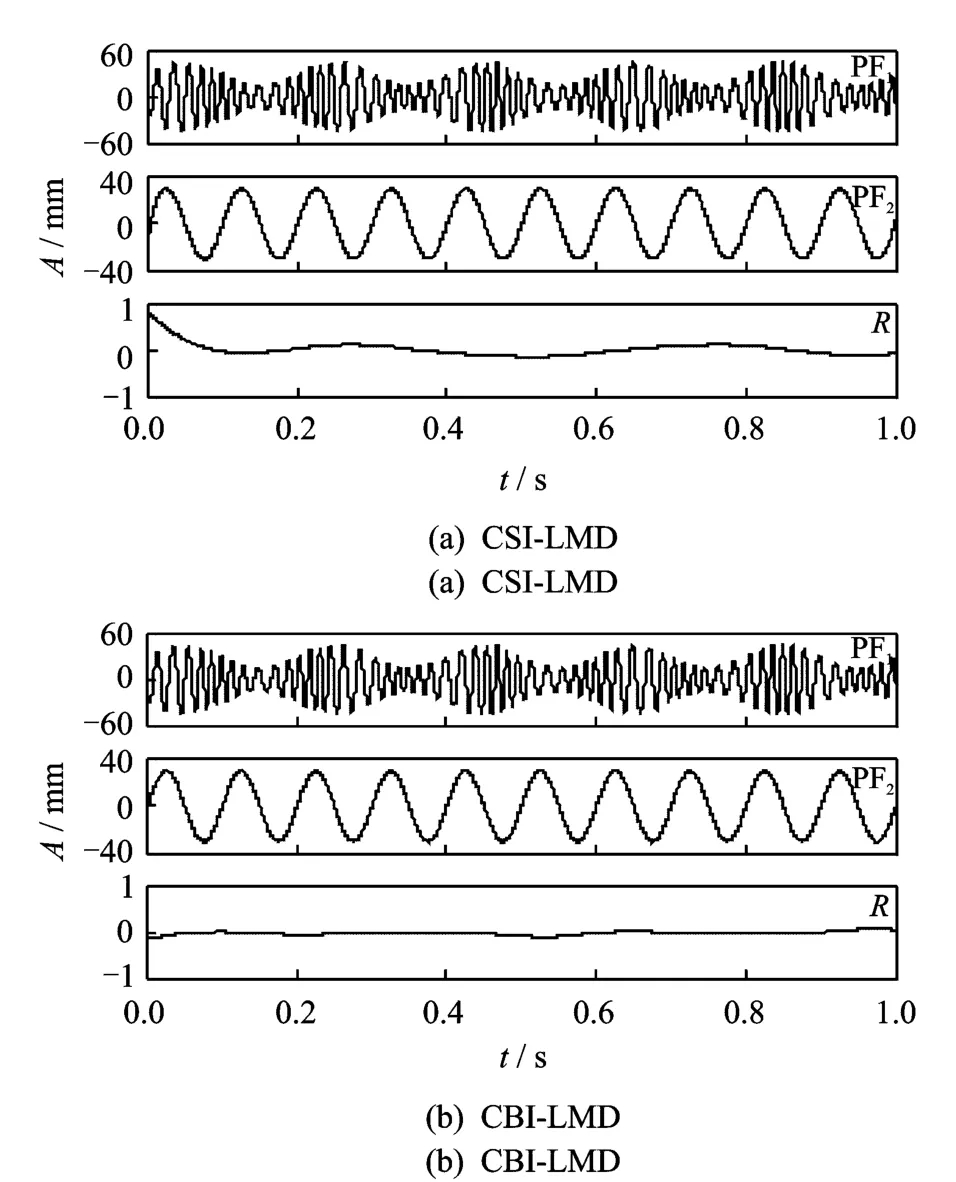
图3 信号x（t）的两种分解结果Fig.3 Two decomposition results of x（t）

图4 PF1的瞬时幅值Fig.4 Instantaneous amplitude of PF1

图5 PF1的瞬时频率Fig.5 Instantaneous frequency of PF1

从图3可见，CSI-LMD和CBI-LMD方法都可以将x（t）分解为两个PF分量和一个剩余分量，PF1，PF2分别对应x1（t），x2（t）。虽然两种方法分解出的PF分量没有明显差别，但是由CBI-LMD方法形成的余量R的幅值很小，经计算，图3（a）与图3（b）中余量R的标准差之比为3.97。在图4，5中，由CSI-LMD方法得到的瞬时幅值和瞬时频率出现了边界效应，尤其是在瞬时频率的端点附近，扭曲现象十分明显。可见，CBI-LMD方法的分解精度更高。

为验证CBI-LMD方法采用OC判据的有效性，引入正交性系数（index of orthogonality，简称IO）对分解结果的正交性进行评价，其定义［14］为

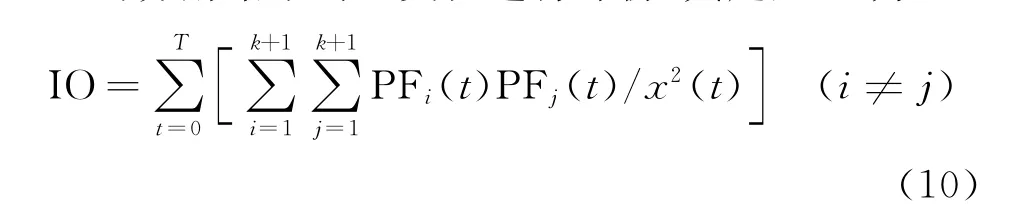
其中：T为信号长度；k+1为PF分量的个数；第k +1个PF分量指剩余分量R。

由式（10）可知，PF分量之间的正交性越好，则IO指标越接近于0。经计算，图3所示两个分解结果的IO指标分别为IOa=0.005 2，IOb=0.000 4，前者是后者的13倍，很明显，CBI-LMD方法分解结果的正交性更好。信号x（t）在分解前后的能量值如下：原始信号为956.25；CSI-LMD为949.91；CBI-LMD为955.83。可见，信号能量在分解前后发生了一定的变化，相比之下，原始信号经CBILMD方法分解后的能量更接近于真实值。

4.2 故障转子振动分析实例

在图6所示的双跨转子实验台上模拟转子不对中故障，并采集振动位移信号，采样频率为5 k Hz，采样点数为3 000。图7为转子转速为2 800 r/min时，原始的故障振动信号经过文献［15］中的消噪方法处理后的时域波形。从图7可以发现，振动信号存在明显的幅值调制特征。对于这种信号，基于平稳过程的信号处理方法只能给出信号的统计平均结果，无法获取其局部化特征，因此必须采用时频分析方法。

图6 转子实验台照片Fig.6 A photograph of the rotor rig

图7 2 800 r/min的不对中故障振动信号Fig.7 A vibration signal of the misalignment fault at 2 800 r/min

利用CSI-LMD和CBI-LMD方法对图7所示的故障振动信号进行分解，两种方法分别得到了4 个PF分量和1个余量R，结果如图8所示。由于分解过程是只依赖于信号自身的自适应过程，因此这些PF分量反映了包涵在振动信号当中频率由高到低的几个自然振动模式。

从图8可见，由两种方法分解得到的PF分量之间存在明显差别。CBI-LMD产生的各个PF分量准确地表征了故障信号中的几个自然振动模式，而CSI-LMD产生的PF1主要包涵了信号分解过程中产生的低幅值虚假分量。该结果说明，相对于CSI-LMD，CBI-LMD的分解性能更好。此外，在信号的分解过程中，记录了两种方法产生每个PF分量所需要的迭代次数和整个分解过程所消耗的时间，如表1所示。表1说明除了PF2之外，CBI-LMD方法产生其他PF分量的迭代次数明显少于CSI-LMD方法的迭代次数；两种方法在分解信号的时间消耗上，差距也十分明显，相差接近于13 s。可见，CBI-LMD方法的分解效率相对较高。利用两种LMD方法产生的PF分量的瞬时幅值和瞬时频率可构成振动信号的时频谱，如图9所示。对图8中存在较大差别的两个PF1进行频谱分析，如图10所示。

图8 转子不对中振动信号的分解结果Fig.8 The decomposition results of the signal in Fig.7

通过对比图9所示的两个时频谱可见，在时频谱的上半部分（高频区），两个时频谱没有明显差别；在时频谱的下半部分（低频区），CBI-LMD方法产生的时频谱线比CSI-LMD方法产生的时频谱线更加完整准确地反映了转子故障振动信号的瞬态变化。

表1 分解过程的迭代次数和耗时Tab.1 The number and the time of decomposition process

图9 两种LMD方法形成的时频谱Fig.9 Time-frequency spectra of two LMD methods

图10 两个PF1的频谱Fig.10 Frequency spectra of two different PF1s

从图10可见，两种LMD方法分解出的PF1的频谱存在明显差别。CSI-LMD方法产生的频谱比较复杂，虽然几条谱线与转子的转频及其谐波成分相对应，但是谱线幅值较小，而且频谱当中还夹杂着相当多的其他成分。CBI-LMD方法的频谱比较清晰准确地显示了转子转频以及几个倍频成分的谱线。

此外，故障振动信号分解前后的能量值以及两种LMD方法所对应的IO值如表2所示。从表2可见，无论是信号分解后的能量变化，还是IO值，CBI-LMD都比CSI-LMD的计算结果要小。这说明笔者提出的CBI-LMD方法具有更好的信号分解性能。

表2 信号分解前后的能量及对应的IO值Tab.2 The energies and IO of the signal in three statuses

5 结束语

在旋转机械的振动信号分析方面，LMD及其改进方法的应用近来受到大量关注。为提升CSILMD方法的性能，利用自适应波形匹配、二次B样条插值以及正交性判据对其进行集成改进，提出了一种新的CBI-LMD方法。通过仿真信号与实验信号对CSI-LMD和CBI-LMD方法的分解性能进行了比较分析。结果显示，CBI-LMD不仅具有更高的分解效率和准确性，而且能够从机械故障振动信号中分离出表征故障特性的振动成分并获得故障特征，是一种分析非平稳机械振动信号的有效方法。

［1］ Yang Yu，Yu Dejie，Cheng Junsheng.A roller bearing fault diagnosis method based on EMD energy entropy and ANN［J］.Journal of Sound and Vibration，2006，294（1-2）：269-277.

［2］ Wang Qinghua，Zhang Youyun，Cai Lei，et al.Fault diagnosis for diesel valve trains based on non-negative matrix factorization and neural network ensemble［J］.Mechanical Systems and Signal Processing，2009，23（5）：1683-1695.

［3］ Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2（5）：443-454.

［4］ Cheng Junsheng，Yang Yi，Yang Yu.A rotating ma-chinery fault diagnosis method based on local mean decomposition［J］.Digital Signal Processing，2012，22（2）：356-366.

［5］ Wang Yanxue，He Zhengjia，Xiang Jiawei，et al.Application of local mean decomposition to the surveillance and diagnostics of low-speed helical gearbox［J］.Mechanism and Machine Theory，2012，47：62-73.

［6］ Feng Zhipeng，Zuo M J，Qu Jian，et al.Joint amplitude and frequency demodulation analysis based on local mean decomposition for fault diagnosis of planetary gearboxes［J］.Mechanical Systems and Signal Processing，2013，40（1）：56-75.

［7］ 胡劲松，杨世锡，任达干.基于样条的振动信号局域均值分解方法［J］.数据采集与处理，2009，24（1）：78-83.Hu Jinsong，Yang Shixi，Ren Daqian.Spline-based local mean decomposition method for vibration signal ［J］.Journal of Data Acquisition＆amp；Processing，2009，24（1）：78-83.（in Chinese）

［8］ 张亢，程军圣，杨宇.局部均值分解方法中乘积函数判据问题研究［J］.振动与冲击，2011，30（9）：84-88.Zhang Kang，Cheng Junsheng，Yang Yu.Product function criterion in local mean decomposition method ［J］.Journal of Vibration and Shock，2011，30（9）：84-88.（in Chinese）

［9］ Zhang Yuan，Qin Yong，Xing Zongyi，et al.Roller bearing safety region estimation and state identification based on LMD-PCA-LSSVM［J］.Measurement，2013，46（3）：1315-1324.

［10］张淑清，孙国秀，李亮，等.基于LMD近似嫡和FCM聚类的机械故障诊断研究［J］.仪器仪表学报，2013，34（3）：714-720.Zhang Shuqing，Sun Guoxiu，Li Liang，et al.Study on mechanical fault diagnosis method based on LMD approximate entropy and fuzzy C-means clustering［J］.Chinese Journal of Scientific Instrument，2013，34（3）：714-720.（in Chinese）

［11］Chen Qiuhui，Huang N，Riemenschneider S，et al.A B-spline approach for empirical mode decompositions ［J］.Advances in Computational Mathematics，2006，24：171-195.

［12］Wang Junbin，Yau H T.Real-time NURBS interpolator：application to short linear segments［J］.The International Journal of Advanced Manufacturing Technology，2009，41（11-12）：1169-1185.

［13］邓蕾，胡小林，李锋，等.基于支持向量机的BS-EMD端点效应消除方法［J］.振动、测试与诊断，2011，31（3）：344-347.Deng Lei，Hu Xiaolin，Li Feng，et al.Support vector machines-based method for restraining end effects of B-spline empirical mode decomposition［J］.Journal of Vibration，Measuremant＆amp；Diagnosis，2011，31（3）：344-347.（in Chinese）

［14］Loutridis S J.Damage detection in gear systems using empirical mode decomposition［J］.Engineering Structures，2004，26（12）：1833-1841.

［15］邓林峰，赵荣珍，龚俊.一种改进的转子振动信号消噪方法研究［J］.仪器仪表学报，2011，32（9）：1961-1966.Deng Linfeng，Zhao Rongzhen，Gong Jun.Research on an improved de-noising method for rotor vibration signals［J］.Chinese Journal of Scientific Instrument，2011，32（9）：1961-1966.（in Chinese）

TN911.7；TH165.3

10.16450/j.cnki.issn.1004-6801.2015.04.017

邓林峰，男，1984年2月生，博士研究生。主要研究方向为机械系统的动态性能测试与分析。曾发表《A vibration analysis method based on hybrid techniques and its application to rotating machinery》（《Measurement》2013，Vol.46，No.9）等论文。

E-mail：denglinfeng2002@163.com

简介：赵荣珍，女，1960年12月生，博士、教授、博士生导师。主要研究方向为旋转机械故障诊断、机械工程测试技术和转子动力学。

E-mail：zhaorongzhen@lut.cn

*国家自然科学基金资助项目（51165019）；教育部高等学校博士学科点专项科研基金资助项目（20136201110004）；兰州理工大学优秀博士学位论文培育计划资助项目（201102）

2013-06-29；

2013-12-12