基于群智能加权核聚类的水电机组故障诊断*

肖 汉，付俊芳，蔡大泉，周建中，肖 剑，付文龙（.河南省电力勘测设计院 郑州，450000）（.华中科技大学水电与数字化工程学院 武汉，430074）

基于群智能加权核聚类的水电机组故障诊断*

肖 汉1，2，付俊芳1，蔡大泉1，周建中2，肖 剑2，付文龙2
（1.河南省电力勘测设计院 郑州，450000）（2.华中科技大学水电与数字化工程学院 武汉，430074）

针对核聚类中核参数选择依赖经验，最优聚类中心难以有效获取的问题，提出了一种仿电磁蜂群加权核聚类算法。首先，考虑不同特征对聚类结果的影响，对样本进行加权处理，利用核空间的Xie-Beni指标建立加权核聚类模型；然后，提出并引入仿电磁蜂群算法求解聚类模型，实现聚类中心、特征权重与核参数的同步寻优。利用该方法分别对3组标准测试样本集以及水电机组故障样本进行聚类测试，并与传统方法进行对比分析。试验结果表明，提出的仿电磁蜂群加权核聚类算法较传统聚类方法具有更高的精度，能够有效实现水电机组振动故障的准确聚类与识别，完成故障诊断。

水电机组；故障诊断；核函数；加权模糊聚类；仿电磁蜂群算法

引 言

目前，我国水电机组正向巨型化方向发展，机组结构日趋复杂，集成化程度越来越高，为保证机组安全经济运行，其故障诊断的作用日渐突显［1］。由于水力发电机组是一个复杂耦合的非线性系统，其故障与征兆间映射关系呈现出较强的不确定性，因此故障模式识别一直是机组故障诊断中的重点研究问题［2-4］。实际工程中由于缺乏先验经验，故难以获取准确、完备的训练样本。模糊核聚类作为一种无监督学习的模式识别方法，在故障诊断中发挥着重要的作用［5-9］。文献［5］将核模糊C均值聚类（kernel fuzzy clustering method，简称KFCM）应用于汽轮机故障诊断，取得了一定成果。文献［6］针对传统KFCM过于依赖样本分布的缺点，提出了加权模糊核聚类的方法并应用于发电机组振动故障诊断。文献［7］提出一种基于动态核聚类分析的水轮机组故障诊断方法，并验证了其有效性。在传统方法中，核参数的选择多依赖于专家经验，主观性较强，而聚类中心通过迭代的方式获取过于依赖初始样本的选择，易陷入局部最优，从而影响聚类结果精度。文献［8-9］分别将混沌优化与引力搜索算法引入到聚类中，用于聚类中心的寻优，取得了不错的效果，然而对不同征兆分类贡献度的考虑尚显缺乏，不能最有效地利用样本特征信息。此外，在算法的全局寻优能力和收敛速度方面还有进一步提升的空间。

人工蜂群算法（artificial bee colony，简称ABC）和仿电磁学算法（electromagnetism-like mechanism，简称ELM）分别为两种新型的群智能优化方法，在不同领域均获得了成功应用［10-13］。两种算法进化策略差异明显，ABC注重保留原个体信息，ELM注重整个种群信息，尤其是当前全局最优解信息的利用。将两种方法结合起来，综合利用两种进化策略，能够有效改善算法的寻优能力与效率。

笔者提出了一种基于仿电磁蜂群加权核聚类算法：给每个样本特征设置权重，表征其贡献度的大小；将聚类中心、核参数以及征兆权重同时作为聚类模型的优化变量，实现其同步寻优；以核Xie-Beni指标［14］为聚类模型的目标函数，获取最佳聚类效果；利用仿电磁蜂群算法进行模型求解，准确高效地完成聚类。通过在水力发电机组振动故障诊断中的应用，验证了该方法的工程实用价值。

1 模糊核聚类模型

1.1 Xie-Beni指标

在传统模糊C均值聚类中，采用聚类结果的紧致性指标作为聚类的目标函数。显然，紧致性指标

其中：zi∈RD为第i类的聚类中心；μik为隶属度。

Xie和Beni在此基础上，引入了分离性指标对各类间隔离程度进行评价，提出了Xie-Beni指标［12］VXB为越小，分类内聚程度越高。给定输入样本集xk∈RD（k=1，2，…，N），分类数为C，则聚类目标函数为

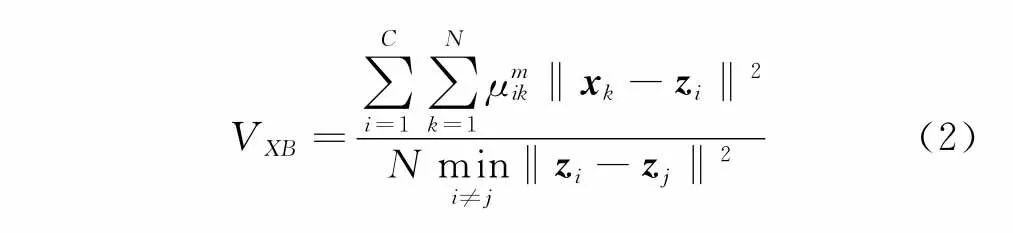
其中：¯xk，¯zi为经过加权处理后的样本与聚类中心；¯xk=xk⊗w；¯zi=zi⊗w，定义运算符“⊗”：x⊗w= ｛x1w1，x2w2，…，xDwD｝；w为样本特征权重向量；Φ（¯xk）为输入样本¯xk在特征空间H中的映射。

核空间内的特征距离为

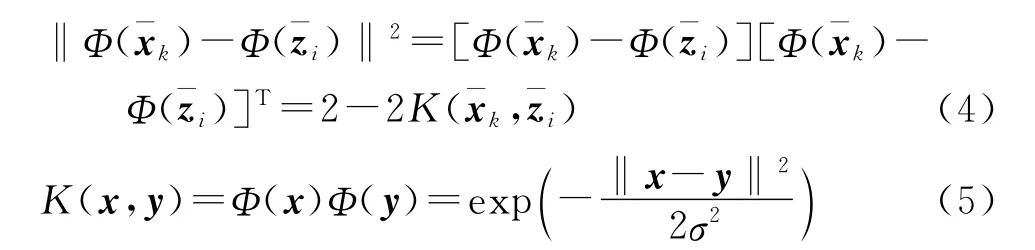
显然，当VXB取极小值时，聚类结果的类内散布最小、类间隔离最大，所对应的数据划分为最佳划分。

1.2 加权模糊核聚类模型

在加权模糊核聚类方法中，对不同特征设置权重，以区分不同重要程度特征对分类结果的影响，从而减小聚类结果对样本分布的依赖程度［15］。同时，利用Mercer核将样本从输入空间映射到特征空间进行聚类。笔者选取高斯核函数，利用核空间中的Xie-Beni指标作为目标函数，建立加权模糊核聚类模型

样本隶属度μik需满足约束条件

根据约束条件式（6），样本隶属度的计算公式为

2 仿电磁蜂群算法

2.1 人工蜂群算法

人工蜂群算法的主要思想是模拟蜂群的智能采蜜行为［16］，通过采蜜蜂、观察蜂和侦察蜂等3种人工蜂分工协作，利用群集智能和随机搜索解决优化问题。设ABC算法初始群含有N个解，每个解代表一个蜜源，用D维向量表示Xi=｛xi1，xi2，…，xiD｝（i=1，2，…，N）。

采蜜蜂和观察蜂根据记忆的蜜源Xi产生新的候选蜜源Vi的更新公式为

其中：j∈（1，2，…，D），k∈（1，2，…，N）均为随机选取，且k≠i。

观察蜂根据蜜源信息，以概率Pi选择蜜源，Pi可表示为

其中：f（Xi）为第i个解的适应度。

若某个蜜源信息，在L次循环之后，仍未得到改善，相应采蜜蜂则放弃该蜜源，成为侦察蜂，按照式（10）对位置区域进行探索。

其中：j∈（1，2，…，D）；rand（0，1）为0，1之间随机数；Xmaxj，Xminj分别为最大和最小值；L为算法中设定的用来控制侦查蜂选择的参数。

2.2 仿电磁学算法进化算子

仿电磁学算法是一种随机全局优化算法，它通过模拟电荷间的吸引和排斥作用机制，求解优化模型［12-13］，其进化机制为

2.3 仿电磁蜂群算法

在ABC算法中，随机搜索只利用解中的一个变量与相邻解进行交叉，这有利于保留原个体信息，但却未能有效利用种群中其他个体的信息。ELM算法不仅利用了所有个体的信息，还充分利用了当前迭代中的全局最优解，这使仿电磁学算法具有良好的收敛速度，但却容易出现局部收敛的问题。笔者将仿电磁学算法与蜂群算法有机结合起来，提出一种仿电磁蜂群算法（electromagnetism-like artificial bee colony，简称ELABC），以蜂群算法为框架，将人工蜜蜂视为自身带有电荷的仿电磁蜂，在采蜜蜂寻找蜜源过程中按照一定的策略引入ELM算法的进化机制，综合利用两种进化机制的优点，提高算法效率。ELABC算法在采蜜阶段候选蜜源Vi的更新公式为

其中：u为控制进化机制选择的权重；r为0到1范围内的随机数。

当r＜u时，候选蜜源按照ABC算法的进化机制来获取；当r≥u时，仿电磁蜂身上的“电荷”将发挥作用，使得候选蜜源通过ELM算法的进化机制获得。在算法执行初期，搜索具有较强的盲目性，需要有效利用全局最优解加快搜索进程，因此选择ELM算法进化机制的概率应更大，即u的取值应较小。在算法中后期，需要更好地保存每个个体的独立信息，以避免局部收敛问题，因此ABC算法进化机制应成为主要选择，即u的取值应较大。综上考虑，笔者将u定义为当前迭代次数m与总迭代次数M的比值

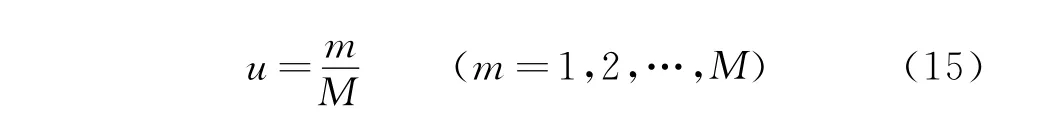
仿电磁蜂群算法的流程如图1所示。

3 仿电磁蜂群加权核聚类

3.1 仿电磁蜂编码与适应度函数

笔者提出了一种仿电磁蜂群加权核聚类算法（electromagnetism-like artificial bee colony weighted kernel clustering，简称EAWKC），利用仿电磁蜂群算法对加权模糊核聚类模型进行求解，获取最优聚类结果。算法中仿电磁蜂个体采用聚类中心zi∈RD（i=1，2，…，C）、特征权重wj（j=1，2，…，D）以及核参数σ混合编码的形式，具体编码如图2所示。

以式（3）为模糊核聚类模型目标函数，建立适应度函数为

图1 仿电磁蜂群算法流程图Fig.1 The flow chart ELABC

图2 仿电磁蜂编码示意图Fig.2 The coding schematic of EAWKC

3.2 仿电磁蜂群加权核聚类

仿电磁蜂群加权核聚类算法流程如图3所示。

图3 仿电磁蜂群加权核聚类算法流程图Fig.3 The flow chart EAWKC

4 水电机组振动故障诊断

4.1 样本测试

如表1所示，选取Iris，Wine，Breast 3组UCI测试数据［6］对EAWKC的性能进行测试，将标准测试样本集分为训练样本和测试样本两部分。首先，根据训练样本利用EAWKC获取聚类中心；然后，分别测试训练样本和测试样本的分类准确性。

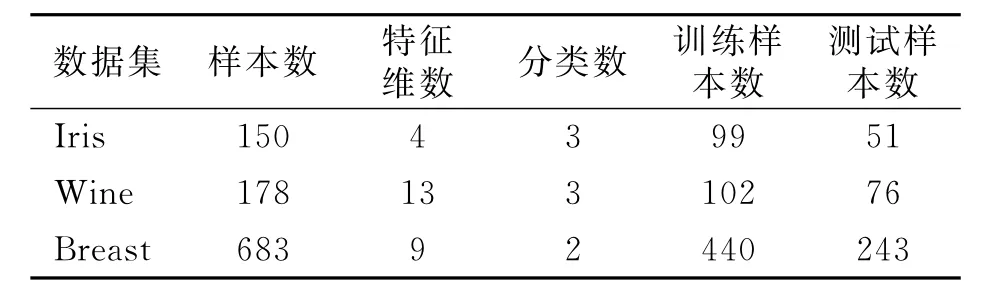
表1 测试数据集Tab.1 Testing data sets

试验分别采用KFCM，K均值聚类（K-means clustering，简称KMC）和EAWKC 3种方法对测试数据集进行聚类。在KFCM和KMC中，迭代终止阈值设为10-6，模糊度m设为2，高斯核参数σ分别选取0.85（Iris），10.6（Wine），2.5（Breast）；在EAWKC中，种群规模N为40，迭代次数设为150，侦查蜂侦查次数上限L设为10，模糊度m同样设为2。试验结果如表2所示。

表2 试验结果Tab.2 The experimental results

试验结果表明，由EAWKC方法获得的聚类模型，无论是训练样本精度还是测试样本精度都明显高于其他两种方法，显然EAWKC能够更有效地获取聚类模型，具有更高的准确性和更强的泛化能力。

4.2 案例测试

笔者利用提出的EAWKC方法对水电机组进行故障诊断，选取某机组的6种常见故障［17］F1～F6：转子不平衡、转子不对中、轴弯曲、动静碰摩、尾水管涡带偏心和水力不平衡。选取9种机组振动信号特征C1-C9：（0.18～0.2）f0，（1/6～1/2）f0，1f0，2f0，3f0和大于50 Hz频谱特征（f0为机组转频）；机组振动分别与转速、负荷、流量的关系特征。故障的训练样本和测试样本分别如表3，4所示。

表3 训练样本Tab.3 The training samples

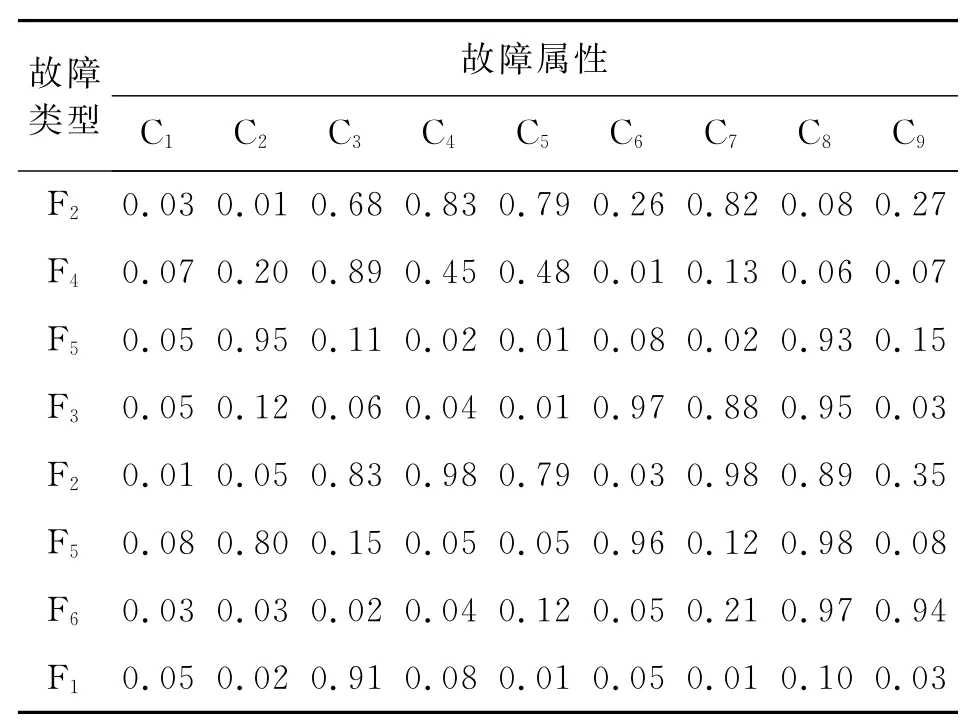
表4 测试样本Tab.4 The testing samples

通过EAWKC方法对样本进行聚类，种群规模N设为40，迭代次数设为150，侦查蜂侦查次数上限L设为10，模糊度m设为2，训练样本被聚为6类分别对应6中常见故障，核函数参数为68.2，聚类中心如表5所示。利用获取的聚类中心对测试样本进行诊断，诊断结果与实际情况完全相符，诊断正确率达到100％。

试验结果表明，笔者提出的EAWKC利用随机搜索算法对特征权重、核参数以及聚类中心进行全局同步寻优，能够更好地利用有效样本特征排除干扰，并自适应调整核参数，准确高效地获取最佳聚类中心，保证聚类的有效性，提高故障诊断结果精度。

表5 聚类中心Tab.5 The cluster center

5 结束语

针对核聚类在水电机组振动故障诊断中核参数选择与最优聚类中心获取的问题，对样本特征赋予权重，并以核Xie-Beni指标为目标建立聚类模型，结合仿电磁蜂群算法，提出了仿电磁蜂群加权核聚类算法EAWKC，并利用该方法有效完成了水电机组故障诊断。结果表明：仿电磁蜂群算法在求解聚类模型的过程中表现出了较高的搜索效率和较强的全局寻优能力；EAWKC通过聚类中心、核参数、特征权重的同步寻优，能够区分不同特征对聚类结果的影响，自适应选择最优核参数，通过样本加权与核函数非线性映射分离有效特征，并利用仿电磁蜂群算法获取最优聚类中心，完成复杂数据的准确聚类。

［1］ 张孝远，周建中，黄志伟，等.基于粗糙集和多类支持向量机的水电机组振动故障诊断［J］.中国电机工程学报，2011，30（20）：88-93.Zhang Xiaoyuan，Zhou Jianzhong，Huang Zhiwei，et al.Vibrant fault diagnosis for hydro-turbine generating unit based on rough sets and multi-class support vector machine［J］.Proceedings of the CSEE，2011，30（20）：88-93.（in Chinese）

［2］ Zhang Xiaoyuan，Zhou Jianzhong，Guo Jun，et al.Vibrant fault diagnosis for hydroelectric generator units with a new combination of rough sets and support vector machine［J］.Expert Systems with Applications，2012，39（3）：2621-2628.

［3］ Xu Chunmei，Zhang Hao，Peng Daogang，et al.Study of fault diagnosis of integrate of D-S evidence theory based on neural network for turbine［J］.Energy Procedia，2012（16）：2027-2032.

［4］ Yu Wenning，Wang Yalin，Gui Weihua，et al.A vibration fault diagnosis system of HGS based on FNN fault detection［C］∥Proceeding of the 6th IFAC Symposium on Fault Detection，Supervision and Safety of Technical Processes.Beijing：［s.n.］，2006.

［5］ 黄保海，李岩，王东风，等.基于KPCA和KFCM集成的汽轮机故障诊断［J］.电力自动化设备，2010（7）：84-87.Huang Baohai，Li Yan，Wang Dongfeng，et al.Steam turbine fault diagnosis based on KPCA and KFCM ensemble［J］.Electric Power Automation Equipment，2010（7）：84-87.（in Chinese）

［6］ 李超顺，周建中，安学利，等.基于加权模糊核聚类的发电机组振动故障诊断［J］.中国电机工程学报，2008，28（35）：79-83.Li Chaoshun，Zhou Jianzhong，An Xueli，et al.Vibration fault diagnosis of generating set based on weighted fuzzy kernel clustering［J］.Proceedings of the CSEE，2008，28（35）：79-83.（in Chinese）

［7］ 刘晓波，黄其柏.基于动态核聚类分析的水轮机组故障模式识别［J］.华中科技大学学报：自然科学版，2005，33（9）：47-49.Liu Xiaobo，Huang Qibai.Classification on the modes of hydro generator unit fault based on dynamic kernel cluster analysis［J］.Journal of Huazhong University of Science and Technology：Nature Science Edition，2005，33（9）：47-49.（in Chinese）

［8］ 李超顺，周建中，方仍存，等.基于混沌优化的模糊聚类分析方法［J］.系统仿真学报，2009（10）：2977-2980.Li Chaoshun，Zhou Jianzhong，Fang Rengcun，et al.Fuzzy clustering analytic method based on chaos optimization［J］.Journal of System Simulation，2009（10）：2977-2980.（in Chinese）

［9］ 李超顺，周建中，肖剑，等.基于引力搜索核聚类算法的水电机组振动故障诊断［J］.中国电机工程学报，2013（2）：98-104.Li Chaoshun，Zhou Jianzhong，Xiao Jian，et al.Vibration fault diagnosis of hydroelectric generating unit using gravitational search based kernel clustering method［J］.Proceedings of the CSEE，2013（2）：98-104.（in Chinese）

［10］Zhang Changsheng，Ouyang Dantong，Ning Jiaxu.Anartificial bee colony approach for clustering［J］.Expert Systems with Applications，2010，37（7）：4761-4767.

［11］Gao Weifeng，Liu Sanyang，Jiang Fei.An improved artificial bee colony algorithm for directing orbits of chaotic systems［J］.Applied Mathematics and Computation，2011，218（7）：3868-3879.

［12］付锦，周步祥，王学友，等.改进仿电磁学算法在多目标电网规划中的应用［J］.电网技术，2012（2）：141-146.Fu Jin，Zhou Buxiang，Wang Xueyou，et al.Application of improved electromagnetism-like mechanism in multi-objective power network planning［J］.Power System Technology，2012（2）：141-146.（in Chinese）

［13］郭壮志，吴杰康.配电网故障区间定位的仿电磁学算法［J］.中国电机工程学报，2010（13）：34-40.Guo Zhuangzhi，Wu Jiekang.Electromagnetism-like mechanism based fault section diagnosis for distribution network［J］.Proceedings of the CSEE，2010（13）：34-40.（in Chinese）

［14］普运伟，金炜东，朱明，等.核空间中的Xie-Beni指标及其性能［J］.控制与决策，2007，22（7）：829-832.Pu Yunwei，Jin Weidong，Zhu Ming，et al.Kernelized Xie-Beni index and its performance［J］.Control and Decision，2007，22（7）：829-832.（in Chinese）

［15］陈平，张钧，鞠萍华，等.汽轮机故障诊断的粒子群优化加权模糊聚类法［J］.振动、测试与诊断，2011（5）：574-577.Chen Ping，Zhang Jun，Ju Pinghua，et al.Weighted fuzzy clustering method based on particle swarm optimization to fault diagnosis of steam turbine set［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2011（5）：574-577.（in Chinese）

［16］Karaboga D.An idea based on honey bee swarm for numerical optimization［R］.Erciyes：Erciyes University，2005.

［17］张孝远.融合支持向量机的水电机组混合智能故障诊断研究［D］.武汉：华中科技大学，2012.

TK72；M6；TP307；TH113

10.16450/j.cnki.issn.1004-6801.2015.04.008

肖汉，男，1987年8月生，工程师。主要研究方向为电厂自动控制、机组状态监测与故障诊断。曾发表《Fault diagnosis for rotating machinery based on multi-differential empirical mode decomposition》（《Journal of Vibroengineering》2014，Vol.16，No.3）等论文。

E-mail：heavennix@126.com

*国家自然科学基金资助项目（51079057，51039005，51109088）

2013-04-27；

2013-07-04