基于奇异值分解的侵彻过载信号降噪方法*

2015-01-12赵海峰李世中中北大学机电工程学院太原03005南京信息职业技术学院机电学院南京20023渥太华大学机械工程学院渥太华KN6N5

振动、测试与诊断 2015年4期

赵海峰，张亚，李世中，郭燕，2（.中北大学机电工程学院太原，03005）（2.南京信息职业技术学院机电学院南京，20023）（3.渥太华大学机械工程学院渥太华，KN 6N5）

基于奇异值分解的侵彻过载信号降噪方法*

赵海峰1，2，3，张亚1，李世中1，郭燕1，2
（1.中北大学机电工程学院太原，030051）（2.南京信息职业技术学院机电学院南京，210023）（3.渥太华大学机械工程学院渥太华，K1N 6N5）

为解决硬目标侵彻过载信号的降噪问题，提出侵彻加速度信号的奇异值分解技术。首先，通过主体奇异值分量稳定原则确定信号的重构子矩阵；然后，利用前K次奇异值能量占优法则提取奇异值的有效阶次，在此基础上对实测信号进行奇异值分解；最后，利用分解出的有效奇异值完成信号的重构。实验证明，经此方法处理的侵彻过载信号可以有效剔除隐含在弹体加速度信号中的振动和噪声，重构后的加速度曲线具有比小波降噪效果更好的信噪比，积分得到的位移曲线能较好反映实际侵彻深度，是侵彻过载信号处理的一种新的可行方法。

侵彻过载信号；奇异值分解；信号重构；信噪比

引言

侵彻过载信号的消噪一直是侵彻测试过程中一个重要步骤。通过对实测信号的分析和处理，可以得出弹体在侵彻过程中的重要参数，为设计弹体的结构强度、装药稳定性和引信可靠性提供重要参考［1］。在侵彻过程中，弹载测试装置测得的过载加速度信号一般包含两种主要成分［2］：a.弹体的刚体加速度由侵彻时弹体所承受的结构阻力形成，是侵彻过程中需要了解的主要成分；b.弹体在侵彻过程中产生的振动信号，包括弹丸横向和纵向的振动信号，在测试过程中是不可避免、需要滤除的成分。侵彻过载信号的处理关键在于找到合适的滤波方法，将侵彻过程中产生的弹体振动信号以及外部噪声剔除，仅保留反应弹体侵彻阻力形成的减加速度信号。

目前，有关侵彻信号的降噪方法国内外学者已经开展了诸多研究。根据其滤波原理的不同主要分为两类。

第1类滤波方法属于测试过程中的机械滤波。其原理是通过在弹内测试装置的前后端或内部加装滤波垫的方法来滤除侵彻过程中弹体的振动信号以及测试环境引起的噪声。张兵等［3］在研究中通过加装3种不同材料（天然橡胶、丁晴橡胶和聚碳铵脂），发现加装滤波垫后测得的加速度信号频率范围有了明显减小，可以分别滤除频率大于4 k Hz，7 k Hz和10 k Hz的信号。文献［4］研制了多种型号的加速度存储测试装置，并较早地采用泡沫铝的方法对测试电路进行缓冲保护，同时对测试所得信号起到机械滤波的功能。上述两种方法在测试中都能够滤除一定频率的噪声，属于机械滤波的范畴，但不具备侵彻信号消噪的普遍性。由于在不同的测试环境下信号存在很大差异，叠加的外部噪声频率也不相同，测试中加装滤波垫的材质、形状和厚度不同，滤波效果也不相同，所以在测试中需要根据实验条件进行分析，按测试环境规律选择合理滤波材质。

第2类滤波方法属于测试信号后的数字滤波法，其核心在于通过对信号的频谱和波形分析，找出弹体侵彻过程中阻力形成的减加速度信号的固有频率，滤除高于此频率的弹体振动信号和环境噪声［5］。此类方法的研究较为广泛，美国Sandia实验室最早在20世纪90年代对所测数据进行3k Hz的频域滤波［6］。Rothacher等［7］计算相邻15点测试数据平均化处理的滤波。文献［8］进行了3k Hz和10k Hz滤波比较。文献［9］提出了弹丸一阶模态临界截止频率滤波。Donoho［10］提出了小波阈值消噪以及基于复杂环境下异常噪声信号的经验模态分解（empirical mode decomposition，简称EMD），都属于测试后的数字滤波方法［11］。这些方法在侵彻信号的处理方面相对机械滤波有着较为广泛的实用性，在滤波降噪的效果上各有短长。

奇异值分解（singular value decomposition，简称SVD）是接近于EMD的一种数字信号处理方法，可以将信号表示为一系列正交分量信号的叠加，分解后的分量具有零相位偏移特性。理想的去相关特性可以从复杂的噪声环境中分离出有用信号的特征分量。近年来常用于图像压缩、数据降维［12-14］、信号故障特征的提取［15］、诊断［16］以及盲信号的分离［17］；但在信号降噪方面的应用很少，尤其缺乏在侵彻过载信号的数据处理方面。笔者在此基础上提出了一种基于奇异值分解的侵彻信号降噪处理方法。首先，通过对实验测得的侵彻过载信号进行奇异值分解，提取侵彻过程中阻力引起的弹体加速度主体信号，剔除伴随的弹体振动信号及外部微弱噪声；然后，进行信号的重构；最后，对重构后的加速度曲线进行去噪效果评定以及侵彻深度的计算和比较。

1 奇异值分解、重构原理

奇异值分解［18］是指：对于实矩阵A∈Rm×n，必定存在m阶正交矩阵U=［u1u2…um］∈Rm×n和n阶正交矩阵V=［v1v2…vn］∈Rn×n，使得式（1）成立。

其中：Σ=dig（δ1，δ2，…，δi）（i=1，2，…，（）

r= min（m，n）），为矩阵A的全部非零奇异值，且满足δ1≥δ2≥…≥δr≥0，Σ中前几个值较大，包含了矩阵A的大部分信息；U和V分别为矩阵的左右奇异阵。

奇异值分解的核心在于通过矩阵运算将一实矩阵分解为正交矩阵U、对角矩阵Σ和正交矩阵V的乘积。其在侵彻过载信号处理过程中的关键在于如何将实验测得的信号序列构造出合适的实矩阵A。

目前，信号奇异值处理中构造矩阵的方法大致可以分为两种。

一种方法是将所测一维时间信号序列S= ［s（1）s（2）… s（ n）］采用连续截取的方式构造矩阵。具体过程可以表示为：取正整数m，n，对所测信号序列按每n个点截取m段，这样可以构造一个

m行n列的包含测试信息的新矩阵A

其中：m≥2；n≥2，且n=int（N/m）。

另一种方法是利用延迟法对测得的时间序列S（N）进行重采样，假设采样间隔为τ（一般取τ= 1），构造所得新的子矩阵B为

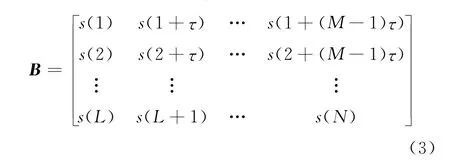
其中：N=L+（M-1）τ；B为L×M维矩阵，秩为r（r≤min（ L，M））。

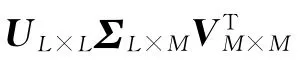
r= min（l，m），δr=0）。

基于奇异值分解的信号子矩阵构造方法原理基本相同，笔者针对侵彻加速度信号时域连续的特点，采用第2种方法进行信号的子矩阵构造。对构造后的子矩阵按式（1）分解，得到r个非零奇异值δi以及l-r个值为0的奇异值。若实验测得的过载信号由侵彻阻力信号和弹体振动及外部噪声构成，则分解后的奇异值δi可以分辨出主体阻力信号和振动及噪声信号的能量集中情况。分解所得的前k个较大的奇异值反映了侵彻过程中弹体承受阻力形成的加速度信号，称为奇异值的有效秩阶次，其余的r-k个奇异值反应弹体的横向和纵向振动信号以及实验环境外部噪声。对重构后的子矩阵奇异值分解后，将反应弹体的横向和纵向振动信号及噪声的r-k个奇异值置零，带入式（1），得到消噪后重构的侵彻过载阻力信号。

2 奇异值分解子矩阵的确定

利用奇异值分解信号降噪的关键在于如何确定测试信号序列的子矩阵行数L，以及找出子矩阵奇异值分解后的前K个有效值。笔者针对侵彻过程中弹体承受的侵彻阻力加速度信号为测试主体成份，弹体振动及外部环境噪声为伴随信号的特点，提出以主体奇异值分量稳定的方法确定子矩阵行数L，以前K次奇异值能量占优原则确定子矩阵的有效阶次K。

2.1 子矩阵行数L的确定

当信号序列取不同行数L进行子矩阵奇异值分解时，定义子矩阵前i次奇异值之和在总体奇异值中所占比例为λi，如式（4）所示，λi代表了奇异值分解前i个奇异值所携带分量信号在总体信号中的比例，且λi呈逐步增大趋势。

当L取某一定值m时，λi为一接近1的数值，表明此次分解的前i次奇异值信息量已经占优。若继续取L=m+1，m+2，…，进行子矩阵重构，λi会因分解后的奇异值接近而变化缓慢，此时可以认为子矩阵的行数m即为重构子矩阵的最佳行数。如果继续增大子矩阵行数取值，对于提取主体信息已经没有任何意义，还会增加奇异值分解的计算量。

2.2 子矩阵有效阶次K的确定

子矩阵有效阶次K的确定可以根据奇异值能量占优原则来确定，即当任一子矩阵进行为奇异值分解时，对应分解后的奇异值为Σ=dig（δ1，δ2，…，δp），此时定义单一奇异值对应信号分量的能量为E，前K次奇异值能量所占总体能量比为P。

若前K次奇异值对应信号分量能量和与总奇异值能量比值P占据很大优势，表明了此次分解前K个奇异值已经代表了信号的主要成分。此时，取K为当前子矩阵的有效奇异值分解阶次即可。

3 仿真信号的奇异值分解

为验证笔者提出的奇异值分解方法的有效性，取与侵彻信号相似的一维电压信号leleccum作为仿真信号，1 350个采样点作为信号的长度进行分析。取L=2，3，4，5，6时进行奇异值分解，信号及对应特征值如图1所示。

图1 Leleccum信号及特征值Fig.1 Lelecuum signal and eigenvalues

采用笔者提出的子矩阵主体奇异值分量稳定原则对信号进行处理。当L=2，3，4，5，6时，其前i次奇异值之和在总体奇异值中所占信息量比例λi变化曲线如图2所示。其中：横坐标为奇异值分量个数；纵坐标为前i个奇异值和在总体奇异值中所占比例。结合图1和图2可知，随着行数L的增加，分解所得的奇异值个数越来越多，分解的奇异值也越来越接近，使得前i个奇异值分量和在总体奇异值中比例λi越来越接近于1。当L继续增大，λi的变化越来越缓慢，表明此时构造的子矩阵经过奇异值分解已近能有效分解出信号所携带的大部分信息，继续增大L没有意义，只会增加计算量。

图2 L取不同值时leleccum信号前i次奇异值信息量变化趋势Fig.2 The tendency of change of leleccum signal former i times singular value information when L take different values

此时，如果设定信号奇异值分解后前i个信号分量占总体信号比为99.7％，由表1可以得出leleccum一维电压信号的子矩阵构造取L=4即可。

表1 L取2，3，4，5，6时leleccum信号λi的数值Tab.1 Theλivalues of leleccum signal when L=2，3，4，5，6

在确定子矩阵行数后，对构造的子矩阵奇异值分解。利用能量比公式计算发现，分解后第1个奇异值分量能量占总体能量比值P为99.6％。这说明第1个奇异值分量携带了信号的主要信息，其余3个奇异值分量携带的为信号微小噪声分量，在信号重构时将其置零即可。

leleccum一维电压信号在L=4，K=1的情况下，奇异值分解结果及分解后误差如图3所示。可以看出，信号经过奇异值分解取得较好的降噪效果，降噪后信噪比为94.84。

图3 leleccum信号特征值、滤波后信号及误差Fig.3 The eigenvalues，reconstructed signal of leleccum and error

4 侵彻实验及信号的奇异值分解

4.1 侵彻实验

为获得侵彻实验信号，采用小型随弹测试系统记录弹体侵彻时的加速度时程曲线。实验设计的测试装置和数据记录系统架构框图如图4，5所示。实验时将小型测试装置装入实验弹弹体底部，用于无限混凝土板靶的侵彻实验。在侵彻过程中，通过加速度计测得弹体侵彻振动信号，经图5中信号适配器的放大、调理，数据记录仪的采样、模数转换后存储在测试装置中的存储器中。在弹体侵彻过程结束后，回收测试装置，通过预留的数据接口读出测得的侵彻加速度数据。某次实验测得的侵彻加速度曲线如图6所示。4.2 侵彻信号的奇异值分解

图4 测试装置Fig.4 The testing device

图5 数据记录系统架构框图Fig.5 Block diagram of data recording system

图6 侵彻加速度曲线Fig.6 The curve of penetration acceleration

1）确定重构子矩阵的行数L。取L=2，3，4，5，8，20时，其分解后的奇异值分量如图7所示。可以看出，当L≥5时，前5个奇异值分量呈下降趋势，之后继续增大L取值奇异值相对变化很小，且基本呈稳定变化态势。此时前i个奇异值之和与整体奇异值比例λi的变化趋势如图8所示。可以看出，λi随奇异值的增加其变化越来越慢，当L=5时，前4个奇异值分量和已经占据总体分量的95％以上，此时取L=5为侵彻过载信号重构子矩阵的行数。

图7 L=2，3，4，5，8，20时侵彻信号奇异值Fig.7 The singular values of penetration signals when L=2，3，4，5，8，20

图8 L取不同值时侵彻信号前i次奇异值信息量变化趋势Fig.8 The tendency of change of penetration signals former i times singular value information when L takes different values

2）在确定子矩阵行数L后，遵循前K次奇异值能量占优原则确定子矩阵的有效阶次K。从表2可以看出，当L=5时，前两个奇异值分别为0.716 和0.112，此后其值都低于0.1，前2次奇异值能量所占总体能量比P为98％，占据了总体能量的大部，说明前2次能量携带了信号的主体，所以取K= 2为奇异值分解的有效阶次。

表2 L取2，3，4，5，8时侵彻信号奇异值数值Tab.2 The singular values of penetration signals when L= 2，3，4，5，8

按上述分析，当L=5，K=2的情况下，侵彻过载信号的奇异值分解结果及分解后误差如图9所示。可以看出，信号经过奇异值分解重构后取得较好的降噪效果。

图9 侵彻过载信号奇异值分解后重构信号及误差Fig.9 The reconstructed signal and error of penetration signals after singular value decomposition

为进一步验证所提出的侵彻过载信号处理方法的正确性，笔者一方面通过与侵彻过载信号的小波分解方法（图10小波去噪后的侵彻过载信号）比较，发现经提出的奇异值分解后重构所得信号的信噪比（signal to noise ratio，简称SNR）要优于小波分解重构后信号的信噪比（见表3）；另一方面，对去噪后的加速度信号在时域进行二次积分，求得弹体侵彻过程的位移时程曲线（见图11）。由图11可知，弹体经降噪后所得侵彻深度为1.003m，与实验测得的实际侵彻深度1.005m（见图12）非常接近。

图10 小波去噪后的侵彻过载信号Fig.10 The penetration acceleration signal after Wavelet filtering

表3 两种不同分析方法信噪比Tab.3 The SNR of two different methods

图11 弹体侵彻的位移积分曲线Fig.11 Displacement-time curve of projectile penetration process

图12 实验侵彻深度Fig.12 Experimental penetration depth

5 结论

1）通过奇异值分解可以将弹体侵彻过程中的主分量信号和伴随的振动及噪声信号分离，从而提取出侵彻阻力形成的主体信号。

2）分解重构后的信号具有较高的信噪比。

3）降噪后的加速度曲线经二次积分所得侵彻深度具有较好的准确度。

4）该方法对于研究侵彻过载信号滤波提供了一种较好的分析思路，对侵彻加速度信号滤波处理具有一定的实际意义。

［1］徐鹏，祖静，范锦彪.高g值侵彻加速度测试及其相关技术研究进展［J］.兵工学报，2011，32（6）：739-744.Xu Peng，Zu Jing，Fan Jinbiao.Research development to high-g penetration acceleration test and its correlative technology［J］.Acta Armamentarii，2011，32（6）：739-744.（in Chinese）

［2］范锦彪，祖静，徐鹏，等.弹丸侵彻混凝土目标减加速度信号的处理原则［J］.探测与控制学报，2012，34（4）：1-6.Fan Jinbiao，Zu Jing，Xu Peng，et al.Impact deceleration signal processing for concrete target penetration ［J］.Journal of Detection＆amp；Control，2012，34（4）：1-6.（in Chinese）

［3］张兵，石庚辰.侵彻硬目标识别技术中的机械滤波［J］.探测与控制学报，2010，32（4）：25-29.Zhang Bing，Shi Gengchen.Mechanical filtering for target recognition of hard target penetration［J］.Journal of Detection＆amp；Control，2010，32（4）：25-29.（in Chinese）

［4］徐鹏，范锦彪，祖静.高速动能弹侵彻硬目标加速度测试技术研究［J］.振动与冲击，2007，26（11）：118-122.Xu Peng，Fan Jinbiao，Zu Jing.Study on acceleration test technique of high velocity kinetic energy projectile penetrating into hard target［J］.Journal of Vibration and Shock，2007，26（11）：118-122.（in Chinese）

［5］郝慧艳，李晓峰，孙运强，等.侵彻过程弹体结构响应频率特性的分析方法［J］.振动、测试与诊断，2013，33（2）：307-310.Hao Huiyan，Li Xiaofeng，Sun Yunqiang，et al.Projectile structural response frequency characteristics analysis method in penetration process［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2013，33（2）：307-310.（in Chinese）

［6］ Franco R J，Platzbecker M R.Miniature penetratator（MINPEN）acceleration recorrder development test［R］.［S.l.］：Sandia National Laboratories，1998.

［7］ Rothacher T，Giger B.High g ballistic flight data recorder［C］∥18th International Symposium on Ballistic.San Antonia：［s.n.］，1999：379-386.

［8］张志安.硬目标侵彻引信半实物仿真技术研究［D］.南京：南京理工大学，2007.

［9］王成华，陈佩银，徐孝诚.侵彻过载实测数据的滤波及弹体侵彻刚体过载的确定［J］.爆炸与冲击，2007，27（5）：416-419.Wang Chenghua，Chen Peiyin，Xu Xiaocheng.Filtering of penetration deceleration data and determining of penetration deceleration on the rigid-body［J］.Explosion and Shock Waves，2007，27（5）：416-419.（in Chinese）

［10］Donoho D L.De-noising by soft-thresholding［J］.IEEE Transactions on Information Theory，1995，41（3）：623-627.

［11］陈隽，李想.运用总体经验模态分解的疲劳信号降噪方法［J］.振动、测试与诊断，2011，31（1）：15-19.Chen Jun，Li Xiang.Application of ensemble empirical mode decomposition to noise reduction of fatigure signal［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2011，31（1）：15-19.（in Chinese）

［12］Phillips R D，Watson L T，Wynne R H，et al.Feature reduction using a singular value decomposition for the iterative guided spectral class rejection hybird classifer［J］.ISPRS Journal of Photogrammetry and Pemote Sensing，2009，64（1）：107-116.

［13］Ahmed S M，Alzoubl Q，Abozahhad M.A hybird ECG compression algorithm based on singular value decomposition and discrete wavelet transform［J］.Journal of Medical Engineering and Technology，2007，31（1）：54-61.

［14］Vanlanduit S，Cauberghe B，Guillaume P.Reduction of large frequence response function data sets using robust singular value decomposition［J］.Computers and Structures，2006，84（12）：808-822.

［15］段向阳，王永生，苏永生.基于奇异值分解的信号特征提取方法研究［J］.振动与冲击，2009，28（11）：30-33.Duan Xiangyang，Wang Yongsheng，Su Yongsheng.The signal feature extraction method based on singular value decomposition［J］.Journal of Vibration and Shock，2009，28（11）：30-33.（in Chinese）

［16］赵学智，叶邦彦，陈统坚.多分辨奇异值分解理论及其在信号处理和故障诊断中的应用［J］.机械工程学报，2010，46（11）：64-75.Zhao Xuezhi，Ye Bangyan，Chen Tongjian.Theory of mlti-resolution sngular vlue dcomposition and its application to signal processing and fault diagnosis［J］.Journal of Mechanical Engineering，2010，46（11）：64-75.（in Chinese）

［17］马杰，王昕，李锵，等.基于特征值和奇异值分解方法的盲分离［J］.天津大学学报，2005，38（8）：741-744.Ma Jie，Wang Xin，Li Qiang，et al.Blind source separation method based on eigen value and singular value ［J］.Journal of TianJin University，2005，38（8）：741-744.（in Chinese）

［18］戈卢布G H，范洛恩C F.矩阵计算［M］.袁亚湘，译.北京：科学出版社，2001：33-72.