GPS大地高高差用于工程土方量计算的探讨

余 力，胡友健，祁亚科，张亚杰

（1.河南省煤田地质局一队，河南 郑州450000；2.中国地质大学（武汉）信息工程学院，湖北 武汉 430074）

GPS大地高高差用于工程土方量计算的探讨

余 力1，胡友健2，祁亚科1，张亚杰1

（1.河南省煤田地质局一队，河南 郑州450000；2.中国地质大学（武汉）信息工程学院，湖北 武汉 430074）

介绍了直接利用GPS大地高高差计算某工程土方量的方法，并将所得结果与用全站仪三角高程测量方法测算的结果进行比较，证明在一定范围内直接将GPS大地高高差应用于工程土方量的测算不仅是可行的，而且可以达到很高的精度。

GPS；大地高高差；土方量测算

1 几种不同高程系统之间的关系

大地高H是地面点沿法线到参考椭球面的距离。H正是地面点沿实际重力（垂）线到大地水准面的距离。H正常是地面点沿正常重力（垂）线到似大地水准面的距离。参考椭球面是为了建立统一的坐标基准而采用数学方法确定的基准面，没有物理意义，只有数学意义。大地高因椭球定位的不同而不同[1-3]。大地高对研究地球形状很有意义，但以往在工程测量中一般不采用。

由图1可知，上述3种高程之间有如下关系：

式中，N为大地水准面差距；ζ为高程异常。

图1 几种高程系统示意图

2 用GPS大地高高差计算工程土方量的可行性探讨[4-6]

如图2所示，设有A、B 两点，其WGS84坐标系下大地高分别为HA、HB，其正常高分别为hA、hB，则有：

式中，ζA、ζB分别为A、B 两点处的高程异常。所以，A、B 两点处的大地高高差为：

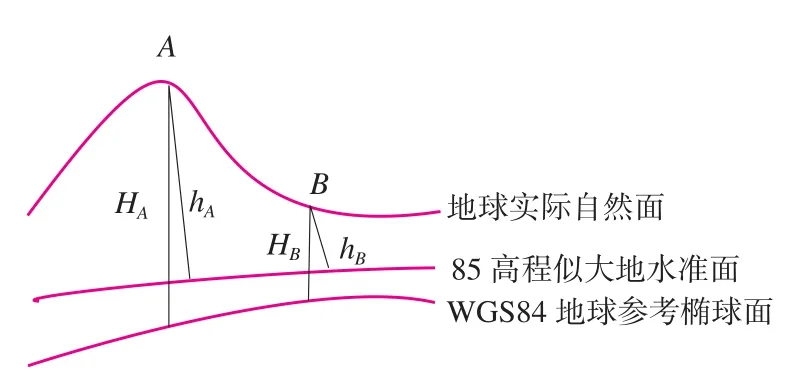
图2 A、B 两点大地高、正常高示意图

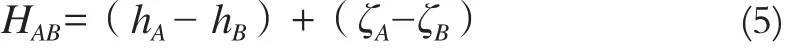
式（5）中,（hA-hB）为A、B 两点间的正常高高差。此时若（ζA-ζB）的值为0，则A、B 两点处的大地高高差与正常高高差是相等的。

众所周知，某点的高程异常值ζ与该点的地球重力场分布密切相关。严格来讲，地面点的高程异常值处处不同，也即（ζA- ζB）的值不可能为0。但是在一定范围内,高程异常值ζ的变化有一定规律。一般来说，在地势平坦的平原地区，距离在不大于30 km的范围内，高程异常值ζ可认为是一致的。而在地势起伏较大的山区，高程异常值ζ与地形走势密切相关，获取一定数量的相关点的高程异常值后可以通过绘等值线法、解析内插法、曲面拟合法等多种数学方法测算其他位置点的高程异常值。

所以，在地形分布不复杂且距离适当的一定范围内，其高程异常值可以近似视为一致，这时（ζA- ζB）的值非常小，可以忽略不计。在相应精度的工程测量中，如果我们只关心相关点之间的高差而不关心其确定的正常高数值，这时我们可以用GPS快速获得其WGS84坐标系下的大地高高差来近似代替正常高高差，进而快速方便地解决工程问题。

3 工程实例[1-3,7]

某市建设高标准农田，需要确定某133.33 hm2项目区平整土地产生的土方量。该133.33 hm2土地位于丘陵地区，总体比较平坦，最高点与最低点之间的高差有20余m。笔者通过如下2种方式验证用GPS大地高高差代替正常高高差进行土方量计算的可行性：

1） 在测区设置分布均匀的5个基准点，分别用水准测量方法测量其正常高高差和用GPS测量其WGS84坐标系下大地高高差，比较这5个点之间的2种高差。

测区内布设的5个基准点如图3所示。经测量获得5个基准点之间的2种高差以及2种高差之差值，如表1所示。

图3 测区内基准点布设示意图

表1 基准点之间的高差值/m

由表1知，H1与另外4个基准点之间的2 种高差之差均在±3 cm以内，因此用GPS大地高高差代替正常高高差来处理相应精度的工程项目是可行的。

2）分别用全站仪法和GPS-RTK法测量测区内整体地形，利用测量数据计算施工产生的土方量，比较2种方法产生的土方量差异，如表2。

表2 不同期土方量计算对照表

由表2知，若视全站仪法测定的土方量为真值，在133.33 hm2范围内用GPS大地高高差计算的土方量差值最大为6 328 m3，最大相对误差为0.63%，其精度完全满足土方量计算对于高差的精度要求。

4 结 语[4-6]

严格来讲， GPS大地高代替水准正常高是难以达到的。但通过数学模型改正，可以在实际工程中用大地高高差代替正常高高差。本文通过具体的工程实例，证明了在一定范围内用GPS大地高高差代替正常高高差是可行的。但需要指出以下几点：

1）GPS大地高高差的精度低于水准测量（三角高程测量）获得的正常高高差精度，在用大地高高差代替正常高高差时需考虑具体工程对高差的精度要求。

2）本文选择的区域具有特殊性（区域面积相对较小，区域内地形起伏不大）。在大范围、地形变化比较复杂的区域，用大地高高差代替正常高高差的适用性还有待进一步研究。

3）用GPS大地高高差代替正常高高差进行相关的施工计算的核心在于相关区域内的高程异常值ζ一致。事实上，高程异常值ζ的确定也是精化区域内似大地水准面的关键工作。若区域内有足够数量的重力测量值，利用重力测量数据和水准测量数据通过建立数学模型来精化区域内似大地水准面，进而用GPS水准来代替传统水准是可以实现的。

[1] 李征航，黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社，2005

[2] 徐绍铨，张华海.GPS测量原理与应用[M].武汉:武汉大学出版社，2001

[3] 孔祥元，郭际明.控制测量学[M].武汉:武汉大学出版社，2006

[4] 徐绍铨，李振洪，吴云孙.GPS高程拟合系统的研究[J].武汉测绘科技大学学报，1999,24(4):336-340

[5] 李征航，包满泰，叶乐安.利用GPS测量和水准测量精确确定局部地区的似大地水准面[J].测绘通报，1994(6):7-12

[6] 魏子卿，王刚.用地球位模型和GPS/水准数据确定我国大陆似大地水准面[J].测绘学报，2003(1):1-5

[7] 张正禄.工程测量学[M].武汉：武汉大学出版社，2005

P208

B

1672-4623（2015）03-0153-02

10.3969/j.issn.1672-4623.2015.03.053

余力，硕士，主要从事大地测量、工程测量等方面的研究。

2014-04-16。

项目来源：2012年河南省地勘基金资助项目。