基于Matlab软件的高等数学教学可视化研究

孔祥强

(菏泽学院数学系，山东 菏泽274000)

0 引言

高等数学是工科院校的重要基础课之一，但对该课程的学习，大多数学生感到很困惑。主要原因是:高等数学中的概念、定理、推导比较抽象，加上教师往往通过传统的教学手段教学，很难生动、形象的把高等数学中的知识点一一解开，但利用Matlab软件，可方便的进行直观演示，使学生一目了然，解开学生的疑惑。Matlab软件是math works公司推出的一套高性能的数值计算的可视化软件，采用了面向对象的技术和矩阵的计算方法。将Matlab软件引入高等数学的教学中，可使抽象的数学可视化，达到调动学生学习的积极性，提高授课效率的目的。

1 重要极限公式的可视化

Matlab提供了很多有关动画制作的函数，借助这些函数可模拟复杂函数的极限等特征。对于实时动画，可利用图形绘制中的擦除属性“erasemode”，从而保持图形窗口中大多数的像素颜色不变，而只更新部分像素颜色，形成运动的图形［1］。

输出

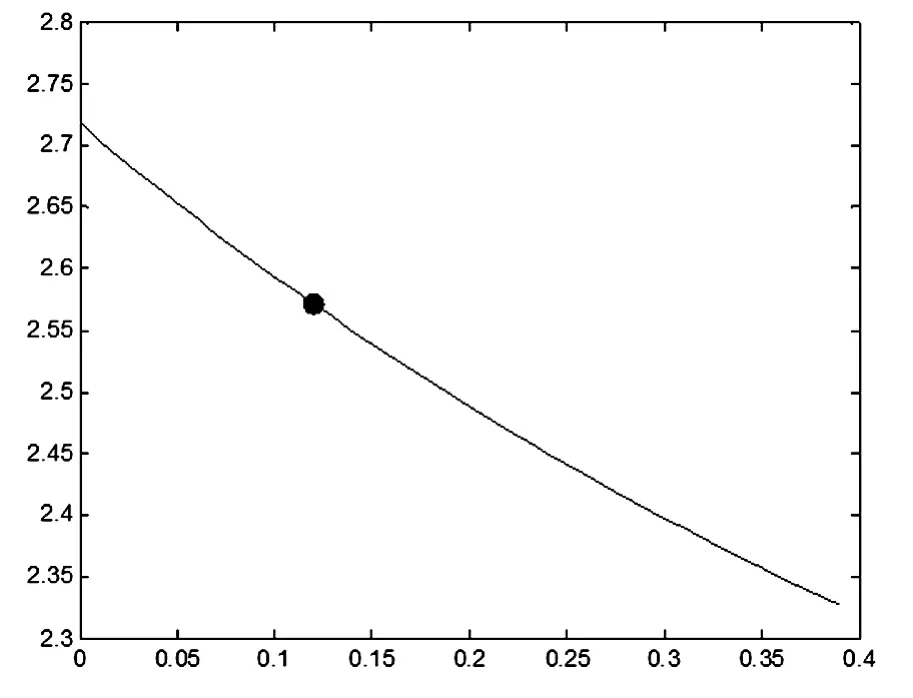
图1 截取动画的一帧

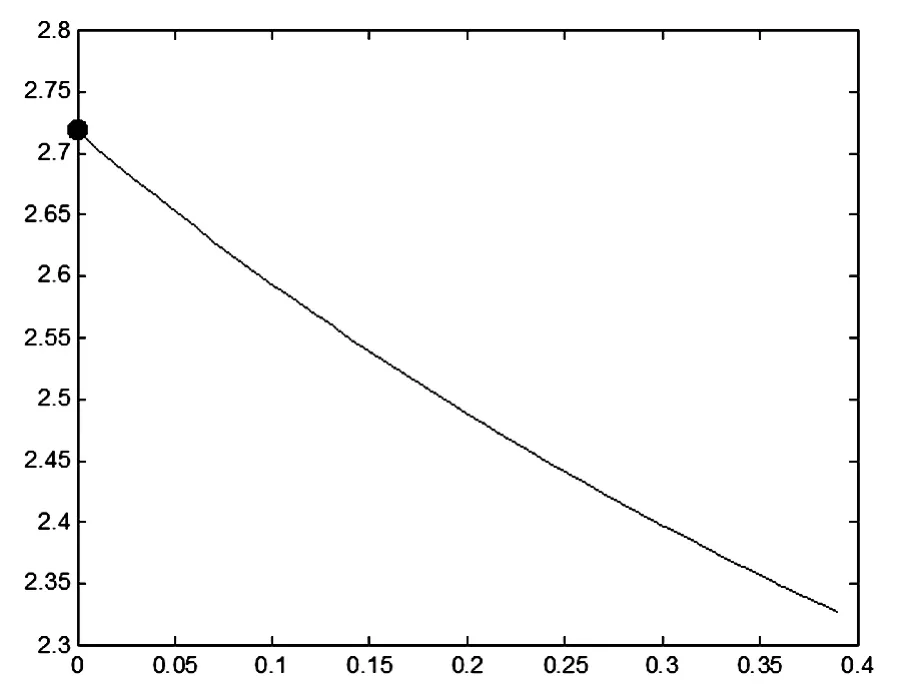
图2 函数最终趋于e

2 函数z=xy的图形性态的可视化

空间曲面是解析几何中的难点部分，如果用手工在黑板上画图，既浪费时间又不精确，学生比较难理解。通过Matlab作图，可很好的克服这些缺点，不但绘制图形变的简单，还可以旋转图形，从不同角度观察图形，更深入了解函数的性态［2］。图3为马鞍面z=xy。在图3的图形窗口中选择view→camera toolbar，通过旋转可得图4，这样，马鞍面的图形就一目了然了。通过图形可得出，函数z=xy在点(0，0)处没有极值，因为依图形，在(0，0)的邻域内，既有大于零的点，又有小于零的点，不符合极值的定义。

输入 x=-11:0.1:11;y=-11:0.1:11;

［x，y］=meshgrid(x，y);z=x.*y;mesh(x，y，z);

rotate3d on;xlabel(＇x 轴＇);ylabel(＇y 轴＇);title(＇z=xy＇)

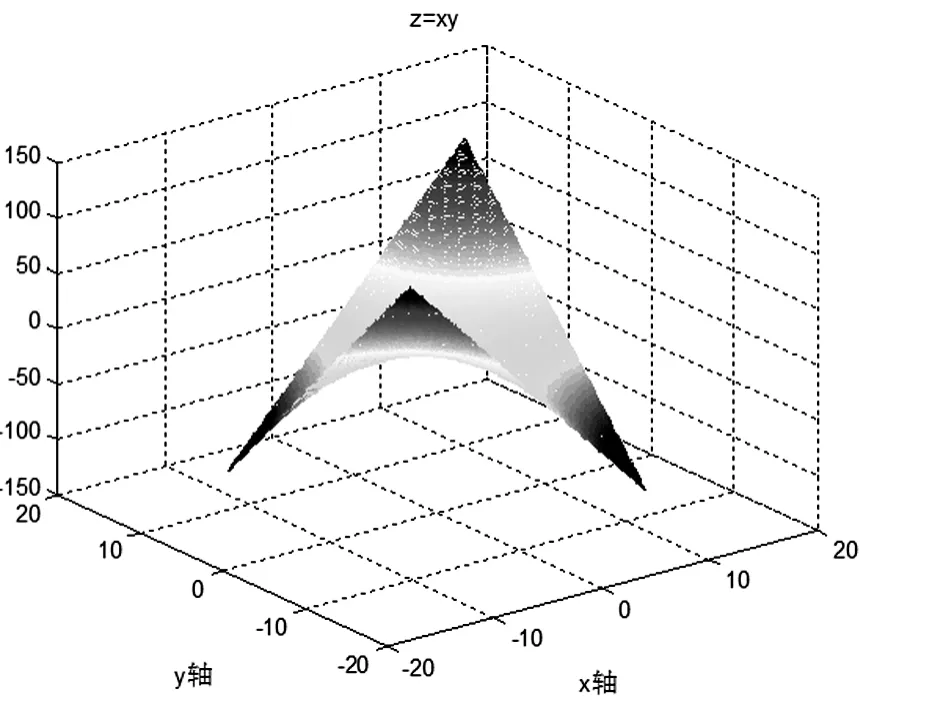
图3 马鞍面z=xy

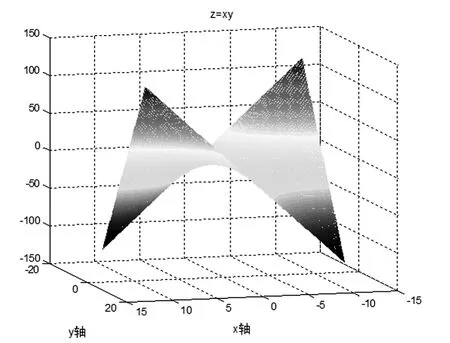
图4 换角度观察的马鞍面z=xy

3 函数极值判定的可视化

求函数极值的方法主要有两种:(1)极值存在的第一充分条件法;(2)极值存在的第二充分条件法［3］。

例如:求函数y=x3-3x2-9x+17的极值。下面用两种方法解决该问题。

(1)第一种方法，先求出函数的导数y'=3x2-6x-9;作出函数y及导数y'的图形，求出驻点后，直接观察图形即可得出驻点是否为极值点，进而可求得极值。

设计方案的质量受参与者个人能力和随机因素的影响。实验结束后对两组参与者的方案平均得分进行了统计，如图5所示。实验组和对照组参与者的个人平均得分可以作为两组参与者能力水平的一个对比。如图5所示，两组人员的能力基本持平，如果以平均得分作为衡量能力的一个指标，实验组的平均能力得分是6.04，对照组是6.05，基本一样。因此，可以认为实验结果展示的差异受参与者个人能力的影响并不大。

输入 syms x

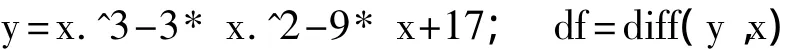
solve(df)

输出df=3*x^2-6*x-9 ans=3 -1

输入 x=-4.5:0.1:4.5;y1=x.^3-3*x.^2-9*x+17;y2=3*x.^2-6*x-9;

plot(x，y1，＇b-.＇，x，y2，＇r--＇)grid on

legend(＇y1=x^3-3x^2-9x+17＇，＇y2=3x^2-6x-9＇)

输出

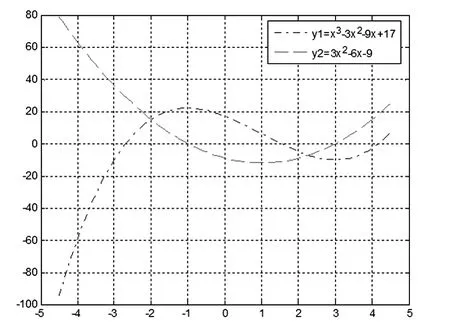
图5 函数y1及其一阶导数y2的图形

从程序及图形可得，函数的驻点为x1=3，x2=-1。在点x1=3的左侧，f'(x)＜0;在右侧f'(x)＞0，故x1=3为函数的极小值点，极小值为-10。在点x2=-1的左侧，f'(x)＞0;在右侧f'(x)＜0，故x2=-1为函数的极大值点，极大值为22。

(2)第二种方法，求出函数的二阶导数，直接从图形中判断二阶导数在驻点处的符号，得出驻点是否为函数的极值点。

输入 syms x

y=x.^3-3*x.^2-9*x+17;df=diff(diff(y，x)，x)

输出 df=6*x-6

输入 x=-4.5:0.1:4.5;y2=3*x.^2-6*x-9;y3=6*x-6;plot(x，y2，＇b--＇，x，y3，＇r:＇)

grid on legend(＇y2=3x^2-6x-9＇，＇y3=6*x-6＇)

输出

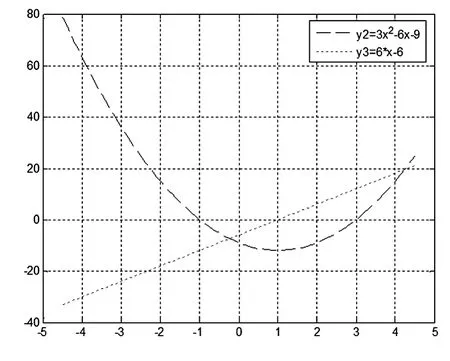
图6 函数y的一阶导数y2及二阶导数y3的图形

从图形可得出，在点x1=3处，f″(3)＞0，故x1=3为函数的极小值点;

在点x2=-1处，f″(-1)＜0，故x2=-1为函数的极大值点。

4 利用matlab对数据的可视化功能，深刻揭示数学知识所描述的客观现象［4］

学生在学习《数学分析》级数一章的时候，往往遇到很多知识没有具体证明，不了解数学知识所反映的具体客观现象。如学习傅立叶级数时，为什么能将一个周期函数展开为傅立叶级数，傅立叶级数与这个周期函数有什么关系等，这些问题困扰着很多同学。利用Matlab对数据的可视化功能，可很容易的解决这些问题。

数学上最简单的表示周期函数的函数是正弦函数和余弦函数，虽然矩形波、锯齿波均不是三角周期函数，但这些非三角周期函数也可以用三角级数的部分和(三角多项式)表示出来，不用过多的理论证明，只需将波形与三角级数的拟合图演示出来，就可得出结论［5］。

输入

t=0:0.01:pi;y0=t/2;y1=sin(t)-sin(2*t)/2;

y2=y1+sin(3*t)/3-sin(4*t)/4;

y3=y2+sin(5*t)/5-sin(6*t)/6;

plot(t，y0，t，y1，t，y2，t，y3)

gtext(＇y0＇);gtext(＇y1＇);gtext(＇y2＇);gtext(＇y3＇)

输出

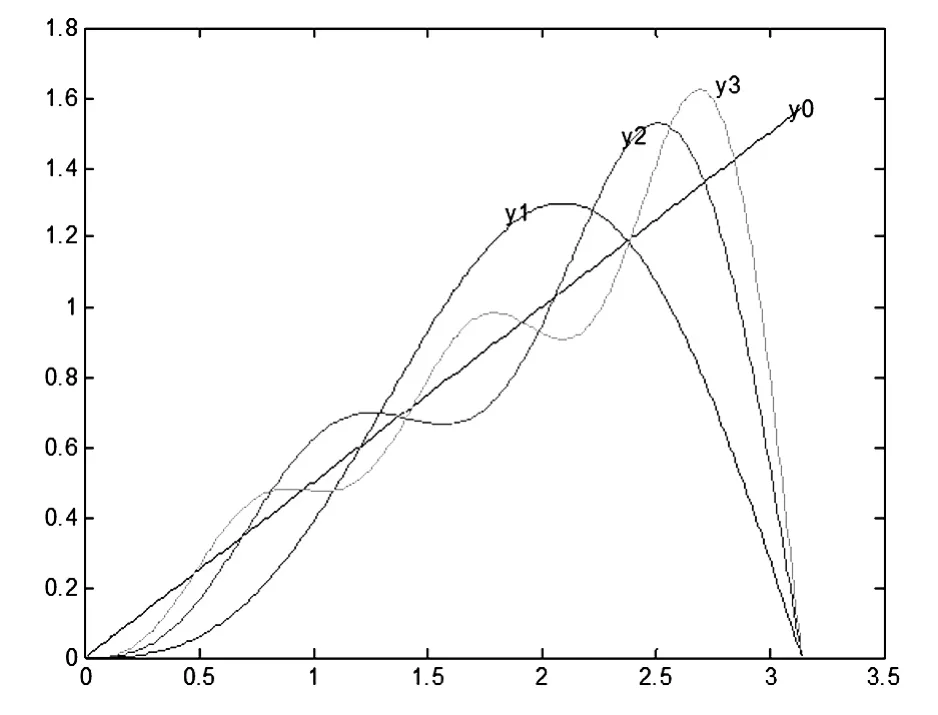
图7 锯齿波与三角多项式的拟合图

通过上面的拟合图可得出，随着三角多项式项数的增加，三角多项式的曲线越来越接近锯齿波的图形，从而得出非三角周期函数也可以用三角多项式表示出来的结论，从而化解了学生对用三角级数表示周期函数理解上的难点。

5 结语

借助于Matlab强大的计算功能和绘图功能，可对任意函数的特性作出初步的判断和分析，以方便进一步解决实际的问题。将大学数学与Matlab结合起来，利用现代科技手段，动态的演示大学数学中的难点问题，使数学的理论、数学的概念不再抽象难懂，有利于培养学生学习的兴趣和应用数学的意识，也为学生以后应用Matlab软件打下了良好的基础。应用Matlab可起到事半功倍的效果，从而可进一步提高教学水平和教学质量，推动高等数学课程的发展［6］。

［1］ 张宏民，王鲁阳，张剑.Matlab在解析几何教学中的应用［J］.高师理科刊，2007，27(3):87-89.

［2］ 于坚.Matlab软件在解析几何教学中的应用［J］.广西教育学院学报，2006(2):16-20.

［3］ 姜启元，邢文训，谢金星，等.大学数学实验［M］.北京:清华大学出版社，2005.

［4］ 张小红，张建勋.数学软件与数学实验［M］.北京:清华大学出版社，2004.

［5］ 朱艳科.MATLAB在大学数学教学和实验中的应用［J］.广西科学院学报，2010，26(1):83-85.

［6］ 张国辉.MATLAB在高等数学中的应用探索［J］.当代教育理论与实践，2009，1(3):105-107.