三种不同监督方法的离群值检测在欺诈交易上的比较

佘玉萍，陈淑清

(莆田学院信息工程学院，福建莆田351100)

0 引言

国内外有众多的学者、专家还有企业的研究机构在各自的应用领域对欺诈检测技术进行了大量的研究与实践，也取得了不少的成果。在国内，文献［1］在分析信用卡欺诈风险成因和识别防范策略的基础上，介绍了支持向量机和决策树这两种算法来进行实证研究。欺诈检测的应用还普遍应用于审计［2］、金融［3］和报税［4］等领域。从欺诈检测算法来看，主要用到了决策树、支持向量机［5］、神经网络［6］。因而目前国内对异常检测方法的研究［7］主要集中于无监督学习框架和一些利用极少数有标号异常样本的监督学习方法。在国外，2002年Bolton等［8］对金融欺诈分析领域的统计方法进行了回顾，探讨了监督学习和无监督学习方法该领域的应用，然而其设计的监督学习方法并未考虑到异常检测中存在的类别分布不平衡。CHANDOLA［9］研究深度挖掘异常产生的原因，并对异常检测的应用场景继续进行了广泛分析，但其依然按异常检测原理方法进行分类，而未能在半监督学习方面深入探讨。因此，本文以某公司的销售数据为例，分别使用无监督、监督和半监督的方法分别来进行较为全面的建模分析，为欺诈交易检测提供更好的指导。

本文以某公司的销售交易数据为测试数据，数据共计401146行，每一行记录包括来自销售员报告的信息。这些信息包括销售员的编号(ID)、产品编号(Prod)、销售员所报告的销售数量(Quant)、总价值(Val)和公司对交易的检查结果(Insp)。其中数据的各变量名与含义如表1所示。有些交易被怀疑为欺诈交易，主要目的是运用数据挖掘工具，为确定是否核查这些提供指导。

表1 样本数据的变量及其含义

数据集中有一列(Insp)含有先前检验活动的信息。其中go rhf 14462条记录标记为ok，1270条标记为fraud，385414条标记为unkn。从已有数据显示还有96%的数据集没标记(unkn)，它们还没有被检验，而只有较小的数据集(大约4%)是有标记的，它们有交易的特征描述和检验结果。在这种情况下，本文尝试使用不同监督技术下的建模方法。

1 建模方法

从确定已有报告是否为欺诈的任务角度来看，这是一个描述性的数据挖掘任务。聚类分析是描述性数据挖掘的一个列子，聚类方法试图对一组观测值形成多个聚类，同一个聚类内的个案相似。相似性通常要求由描述观测值的变量所定义的空间给出一个距离定义。距离是衡量一个观测值与其他观测值之间距离的函数。距离靠近的个案通常认为属于同一组。离群值检测也是描述性的数据挖掘任务。有些离群值检测方法假定数据的预期分布，把背离这一分布的任何值标记为离群值。另一个常见的离群值检测策略是假定一个变量空间的距离度量，然后把距离其他观测值“太远”的观测值标记为离群观测值。本文分别从机器学习的三种不同技术对应的三种模型来对同一组交易数据进行离群值检测。

1.1 无监督学习技术

基于聚类的离群值排名(Clustering-Based Outlier Rankings，ORh)方法［10］采用分层聚类法获得一个给定数据集的聚类树。主要的思想是:以聚类树的信息为基础进行离群值的排序。离群值不易于合并，因此当它们最终被合并时，它们合并前所属类的大小和它们被合并进去的类的大小应该相差很大。这也反映了离群值和其他观测值是很不相同的。少数情况下，离群值与其他观测值的合并发生在初始阶段，但这只限于类似的离群值，否则离群值的合并会在聚类过程的后期合并。这种方法使用下面方法来计算每一个个案的离群值分数。

1)对于每一个合并两个组(gx，i和gy，i)的第i步，得到离群因子值of(outlying factor)为:

其中gx，i是x所属的组，而|gx，i|是该组的大小。因为感兴趣的是较小的组，所以参与合并的两个组中较大组的成员离群值分数将被赋为0。在分层聚类算法的整个迭代过程中，每个观测值可以参与多个合并过程，有时是较大组的成员，有时是较小组的成员。

2)数据集的每个个案的最终离群值分数由下面的公式算出:

得到的实验结果是基于预先定义的检验限制值为10%来计算决策精确度和回溯精确度。以下两组模型的实验前提条件与此相同。

1.2 监督学习技术

AdaBoost.M1［11］是属于监督学习的一种算法，每个用来训练的样本被赋予一个权重，权重的大小代表了该样本被下一个弱分类器列入训练样本集的概率。首先考虑一个二分类问题，并假设训练样本集为:S={(x1，y1)，…，(xm，ym)}，其中 xi属于实例空间 X，有 xi∈X;yi是类别标志，yi属于类别空间 Y，有 yi∈Y∈{+1，-1}。初始化时对所有的训练样本赋予相同的观测权重1/m。然后，使用弱分类器对训练集进行训练，每次训练后，根据训练结果更新训练样本的观测权重，并按照新的权重分别进行训练。反复迭代T次，最终获得一组弱分类器序列h1，…，hT，每个弱分类器都具有一定的权重，分类效果好的弱分类器观测权重较大，反之较小。最后，通过加权的方法合并全部弱分类器，进而生成最终的强分类器H。Ada Boost.M1算法有很多优点，首先简单易用，除了迭代次数T以外，不需要调节任何参数;其次，寻找一个精度比随机预测略高的弱学习算法比寻找一个高精度的强学习算法要容易得多;最后，它具有理论支持，只要有足够的数据以及弱分类器就能够达到任意预测精度。

从实验结果看出，在10%的检验水平下，标准的Ada Boost.M1比ORh有较高的决策精确度和回溯精确度。

1.3 半监督学习技术

自我训练模型［12］是一个众所周知的半监督分类形式。该方法先用给定标记的个案来建立一个初始的分类器。然后应用这个分类器来预测给定训练集中未标记的个案。将分类器中有较高置信度的预测标签对应的个案和预测的标签一起加入到有标记的数据集中。在这个新的数据集上得到一个新的分类器，继续重复这个过程，直到达到某个收敛准则时迭代过程才停止。只要能输出预测的置信度信息，那么基本分类算法都可运用该方法。本文采用AdaBoost.M1模型作为训练模型来完成实验测试。

从实验结果看出，在10%的检验水平下，自我训练的Ada Boost.M1模型(Ada Boost.M1-ST)比标准的Ada Boost.M1和ORh均有较高的决策精确度和回溯精确度。

2 评价模型的准则及结果分析

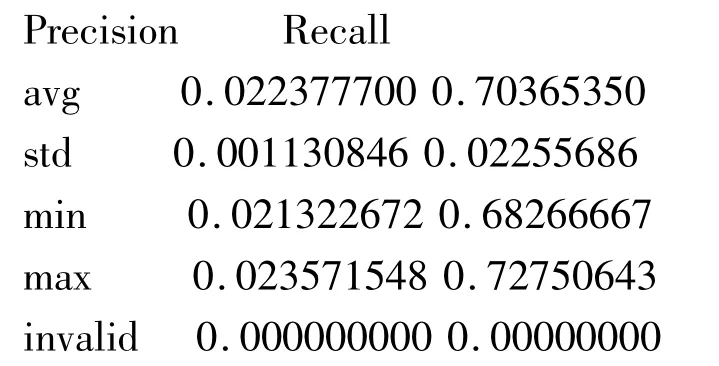
当给出检测报告的一个测试集时，每个模型将会产生排序，如何评价这些排序。当目标是预测一个小集合的罕见事件(如欺诈)时，决策精确度和回溯精确度［13］是合适的评价指标。而决策精确度和回溯精确度曲线(Precision/Recall Curve)是对这两者的一种可视化表示。对于不同的限制水平(即检测更少或更多的报告)进行迭代，得到不同的决策精确度和回溯精确度。某些模型给出测试集中每一个观测值的离群值排序分数，这些分数的取值范围为0～1。分数越高，说明这个观测值是欺诈交易的模型置信度就越高。如图1所示。

评价模型的另一准则是根据阳性预测率(RPP，Rate of positive predicitions)所捕获的检验限制得到的回溯精确度［13］，对应的曲线为累积回溯精确度图(Cumulative Recall Curve)。对于累积回溯精确度图而言，模型的曲线越靠近左上角，模型越好。如图2所示。

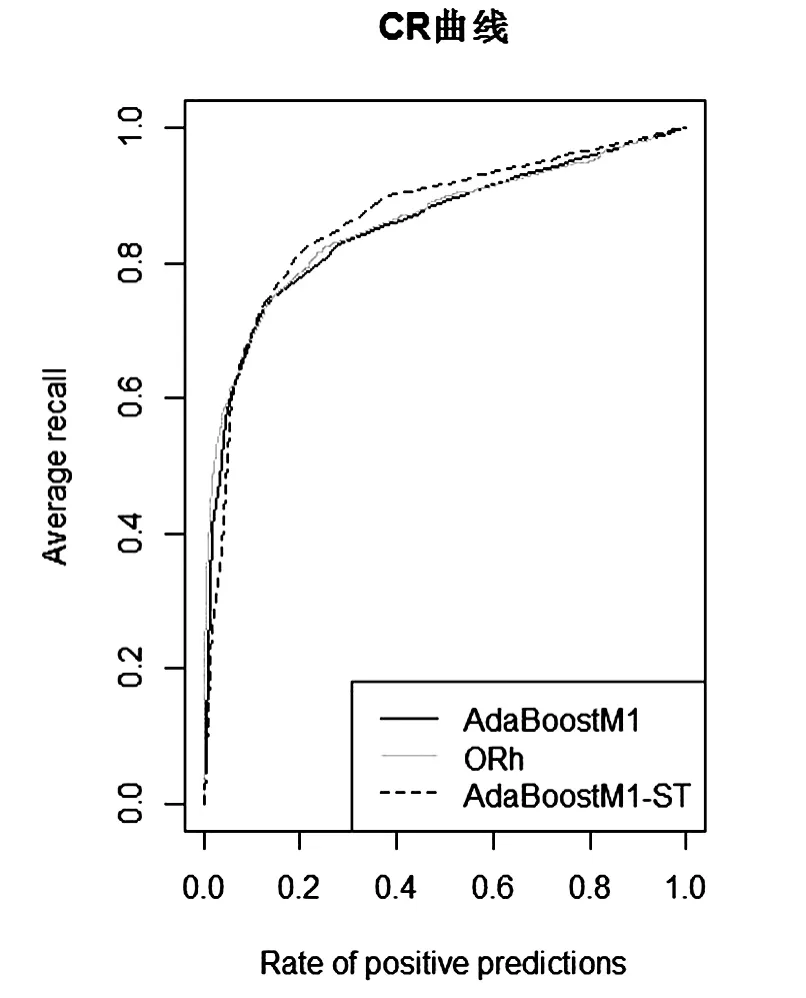
图1 标准的Ada Boost.M 1模型、ORh模型和自我训练的Ada Boost.M 1模型的CR曲线

图2 标准的AdaBoost.M 1模型、ORh模型和自我训练的AdaBoost.M 1模型的PR曲线

从图1的实验结果可以看出，在欺诈交易检测问题的三种模型中，CR曲线确认了自我训练的AdaBoost.M1模型(AdaBoost.M1-ST)是最好的模型。尤其是在检验限值水平在15%至20%时，明显要优于其他的模型。但就决策精度(PR曲线)而言，对低水平的回溯精确度值，这个模型的分数不是那么理想，甚至比Ada-Boost.M1模型和ORh模型都要差，然而对于较高的回溯精确度值，该模型就体现出它的优势。这里较高的回溯精确度水平恰恰是销售欺诈检测应用所需要的。总之，对销售数据的欺诈检测这个应用而言，Ada-Boost.M1-ST模型是一个很有竞争力的模型。

3 结语

离群值检测研究是一个非常有应用价值的问题，近年来受到越来越多的讨论与关注，但由于离群值的相对性和主观性。在不同应用的海量数据中挖掘离群值是相当复杂的，至今没有高效且通用的方法来检测离群值。本文主要从机器学习的三种不同技术出发，分别从对应的三种模型来应用于销售数据中欺诈交易的检测，并从实验数据来分析这三种模型的检测性能，对这类问题具有一定的指导性。但对于其他领域的应用还缺乏实验验证，所以暂且不具备所有应用的普遍指导意义。

［1］ 吴婷.数据挖掘在信用卡欺诈识别上的应用研究［D］.南京:东南大学，2006.

［2］ 黄晓辉，张四海，王煦法.基于免疫网络的分类应用于审计欺诈检测［J］.计算机工程与应用，2005(29):204-207.

［3］ 曹长修，王 越.KDD方法在金融欺诈检测中的应用研究［J］.计算机工程与设计，2002，23(5):43-45.

［4］ 王世卫，李爱国，郭媛媛等.基于SGNN的报税欺诈检测［J］.西安科技大学学报，2004，24(4):470-473.

［5］ 徐永华.基于支持向量机的信用卡欺诈检测［J］.计算机仿真，2008，28(8):376-379.

［6］ 凌晨添.进化神经网络在信用卡欺诈检测中的应用［J］.微电子学与计算机，2011，28(10):14-17.

［7］ 陈斌，陈松灿，潘志松，李斌.异常检测综述［J］.山东大学学报(工学版)，2009，39(6):13-23.

［8］ BOLTON R J，HAND D J.Statistcal fraud detection:a review［J］.Statistical Science，2002，17(3):235-255.

［9］ CHANDOLA V，BANETJEE A，KUMRY V.Anomaly detection:a survey［J］.ACM Computing Surveys，2009，41(3):1-58.

［10］ Torgo，L.Resource-bounded Fraud Detection［C］∥ in Progress in Artificial Intelligence，13th Portuguese Conference on Artificial Intelligence，EPIA，Neves et.al(eds.).LNAI，2007:449-460.

［11］ R.E.Schapire，Y.Singer.Improved boosting algorithms using confidencerated predictions［C］.Machine Learning 37，1999:297-336.

［12］ Chuck Rosenberg，Martial Hebert，and Henry Schneider man.Semi-Supervised Self-Training of Object Detection Models［C］∥ Processings of the 7th IEEE Workshop on Application of Computer Vision.IEEE Computer Society，2005:29-36.

［13］ Davis，J.，Goadrich，M.The relationship between precision-recall and ROC curves［C］∥Proceedings of the 23rd International Conference on Machine learning.ICML ’06，New York，2006:233 –240.