关于等价无穷大量代换求极限的补充

李红菊，丁 健

(安徽新华学院公共课教学部，合肥230088)

0 引言

极限理论是微积分学说的基础，求函数的极限也是学生学习中常见的一类题型，其方法是多样的，而等价代换就是众多方法中最有效的一种。1986年，邹兆南［2］引入了无穷大阶的概念，讨论了幂函数、指数函数与对数函数的无穷大的阶，证明了无穷大的运算法则和在乘除运算中的等价替换定理，此后等价无穷大量的应用受到众多学者的关注，尤其是利用等价无穷大量代换求极限［3-10］，这是因为一方面等价无穷大量代换可达到简化极限运算的目的，但另一方面该方法也很容易导致出错。2009年，郑婕［6］系统的研究了等价无穷大量在极限运算中的四则运算和乘方运算的条件和结论，文中对于加法运算的结论为:设α(x)、α1(x)、β(x)、β1(x)皆为1时的无穷大量，且1，1，若1存在且不等于1，则α(x)-β(x)～ α1(x)-β1(x)?(x→x0)。展丙军［7］等人讨论了无穷大量的比较，定义了高阶无穷大量、低阶大量和(A≠1)阶无穷大量等概念，并举例讨论了其在级数敛散性判定中的应用;李昌文［8］等人讨论了等价无穷小量和等价无穷大量的一个误区;孙卫卫［1］等人阐述了等价无穷大量在(A≠1)、(A≠1)、(A≠1)、(A≠1)和(A≠1)型未定式的计算中等价代换的条件，并将文献［6］中的减法运算推广至在某个极限过程中(A≠1)(A≠1)或为无穷大的情形。大量的文章研究了极限运算中等价无穷大量的乘除运算，而加减运算研究的较少。本文主要研究在某个自变量的变化过程中时等价无穷大量的减法运算，得到了该条件下无穷大量等价代换的一个充分条件，丰富和完善了无穷大量的等价代换理论。

1 预备知识

定义1［7］设函数f(x)和g(x)是在自变量的某个变化过程中的无穷大量，且也是在这个变化过程中的极限。

注2:定义2中自变量的变化过程也可以为x→-∞和x→+∞。

为了叙述的方便，已以下皆假设x→x0是大于零的常数。

2 主要结论

由定义1和定义2易得性质1。

性质1若在x→x0时rank［f(x)］=k，则在x→x0时x→∞是关于x→∞的同阶无穷大量;若在x→∞时rank［f(x)］=k，则在x→∞时xk是关于xk的同阶无穷大量。

性质2若在自变量的同一变化过程中，rank［f1(x)］=k1＞0且 rank［f2(x)］=k2＞0，则rank［f1(x)f2(x)］=k1+k2。

证明:假设 x→ x0时 rank［f1(x)］=k1且 rank［f2(x)］=k2，则

rank［f1(x)f2(x)］，rank［f1(x)f2(x)］。

所以 rank［f1(x)f2(x)］，

即rank［f1(x)f2(x)］=k1+k2。在自变量的其它变化过程中的结论可类似证明。

性质3 若在自变量的同一变化过程中，rank［f1(x)］=k1＞0且 rank［f2(x)］=+∞，则rank［f1(x)f2(x)］=+ ∞。

性质6若f1(x)和f2(x)是在自变量的同一变化过程中的两个无穷大量，则

证明:假设该极限过程为 x→x0.若rank［f1(x)］=+∞或rank［f2(x)］=+∞，结论显然成立;现假设rank［f1(x)］=k1且 rank［f2(x)］=k2，则，则A必为常值，所以rank［f1(x)-f2(x)］≤k1.在自变量的其它变化过程中的结论可类似证明。

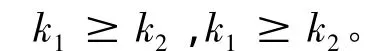
在文献［1］和文献［3］研究的基础上，本文仅研究等价无穷大量在极限减法运算中的如下情形。

定理2设在自变量的某个变化过程中，函数 γ(x)、γ(x)、γ(x)、γ(x)、γ(x)皆是无穷大量且rank［α(x)- α1(x)］ ＜ rank［γ(x)］。若 rank［α(x)- α1(x)］ ＜ rank［γ(x)］且 rank［β(x)- β1(x)］ ＜rank［γ(x)］，则

证明:若 rank［α(x)- α1(x)］＜ rank［γ(x)］且 rank［β(x)- β1(x)］＜ rank［γ(x)］，则由性质4 和性质5可知，所以由定理1可知结论成立。

3 应用举例

4 结语

本文在无穷大量阶的概念的基础上，得到了极限运算中等价无穷大量加减运算的一个新的充分条件，丰富和完善了无穷大量的等价代换理论，但是如何确定无穷大等价代换后误差的阶，还没有特别好的办法，值得进一步的研究。

［1］ 孙卫卫，孙建英.等价无穷大在未定式计算中的应用［J］.哈尔滨师范大学自然科学学报，2014，30(3):69-72.

［2］ 邹兆南.无穷大的阶及其运算法则［J］.重庆交通学院学报，1986，2(17):114-120.

［3］ 甘以炎.等价无穷大及其渐近表示式［J］.葛洲坝水电工程学院学报，1996，18(4):83-85.

［4］ 常庚哲.关于无穷大量的等价［J］.高等数学研究，2000，3(3):13-15.

［5］ 王梅英，陆伟东.无穷小与无穷大的阶在极限运算及判级数敛散性中的应用［J］.南京审计学院学报，2007，4(2):73-76.

［6］ 郑婕.等价代换在极限求解中的应用［J］.中国教师.高等教育，2009(1):206-207.

［7］ 展丙军，展铭望.无穷大量的性质及妙用［J］.大庆师范学院学报，2011，31(3):67-70.

［8］ 李昌文，潘亚丽.关于无穷小与无穷大的几个教学误区［J］.淮北师范大学学报(自然科学版)，2013，34(4):90-93.

［9］ 刘桂仙，刘庆升.求极限的等价无穷大代换［J］.高等数学研究，2014，1(1):51-52.

［10］ 马志良.无穷大量与无穷大量的等价［J］.数学学习与研究，2014(7):74.