钢—混凝土混合结构体系屈曲模态判别标准及临界荷载简化算法

李亮+李国强

摘要：为了研究核心筒支撑作用对屈曲模态和屈曲临界荷载的影响，建立了钢-混凝土混合结构体系简化力学模型，并在大量有限元分析的基础上，研究了钢-混凝土混合结构体系中框架和支撑两部分之间的相对强弱关系对屈曲模态的影响。根据屈曲模态不同，将钢-混凝土混合结构体系划分为4种类型，归纳出可靠的屈曲模态判别标准，并提出了与各类屈曲模态对应的临界荷载简化算法。研究结果表明：该简化算法计算结果准确、可靠，可供设计人员采用。

关键词：钢-混凝土混合结构体系；支撑作用；屈曲临界荷载；简化力学模型；有限元分析

中图分类号：TU375.4 文献标志码：A

0 引 言

钢框架-混凝土核心筒混合结构是由钢框架与混凝土核心筒组成的共同承受竖向荷载和水平荷载作用的高层建筑结构[1-4]。钢框架强度高、自重轻、构件截面小、楼面跨度大，主要用于承受竖向荷载；混凝土核心筒造价低，侧向刚度大，主要用于承受风和地震等水平荷载作用[2]。在钢框架-混凝土核心筒混合结构中，与框架部分单独承受竖向荷载时的屈曲临界荷载相比，由于混凝土核心筒往往具有富余的抗侧能力，会对钢框架起到侧向支撑作用，因此当结构发生屈曲时框架所承担的竖向荷载往往远大于其独立承担竖向荷载的屈曲承载力[4-5]。

本文系统研究了钢-混凝土混合结构体系中框架和混凝土核心筒之间的相对强弱关系对结构屈曲模态的影响。根据屈曲模态不同将钢-混凝土混合结构体系划分为4种类型，归纳出可靠的屈曲模态判别标准，并提出了各类屈曲模态对应的临界荷载简化计算公式，可供设计人员采用。

1 钢-混凝土混合结构体系

钢-混凝土混合结构通过楼盖将钢框架和混凝土核心筒连接为一体，共同承担水平荷载和竖向荷载，如图1所示。由于钢-混凝土混合结构受力合理、经济指标优越，被认为是一种符合中国国情的高层建筑结构体系。在实际工程中，如何合理地考虑混凝土核心筒的支撑作用，准确地估计框架部分的屈曲临界荷载受到了广泛的关注[6-7]。筒体、剪力墙可近似看作是弯曲型竖向悬臂杆，由于核心筒中层与层之间存在相互作用，使得核心筒对框架的支撑作用不宜采用层模型来分析，而需要建立整体模型进行研究[8-9]。

对于轴力不变的情况，童根树等[4]采用静力法对顶点竖向集中荷载作用下的双重抗侧力结构屈曲问题进行研究，得到了屈曲临界荷载的计算公式，结构体系简化模型如图2所示，其中，w（x）为作用的分布外荷载，q（x）为2个结构之间通过连杆的相互作用力，P1，P2分别为作用在结构1和结构2顶端的竖向集中荷载，H为结构的高度，QH为水平剪力。

Rosman[10]讨论了剪力墙-框架双重抗侧力结构的稳定性，假定框架为刚度沿高度不变的纯剪切竖向悬臂杆，剪力墙为刚度沿高度不变的纯弯曲竖向悬臂杆，且荷载沿高度均匀分布，给出了结构整体临界荷载的计算表格，然而由于假定结构发生整体失稳，不能考虑局部失稳的情况，因此这个表格的应用价值有限。

考虑到在竖向均布荷载作用下，轴力沿高度是变化的，采用静力法推导屈曲临界荷载计算公式过程中需要求解高阶变系数微分方程，难以得到屈曲临界荷载的理论计算公式[9-10]。2 简化力学模型

钢-混凝土混合结构中的抗侧力构件包括混凝土核心筒和钢框架2个部分。根据抗弯刚度和剪切刚度相等原则，可将空间钢框架和混凝土核心筒分别等效为平面总框架和总剪力墙，楼板等效为两端铰接的刚性连杆。

纯粹从力学角度考虑，平面总框架可进一步简化为以剪切变形为主的弯剪型竖向悬臂杆，总剪力墙可简化为以弯曲变形为主的弯剪型竖向悬臂杆，如图3所示。

3 有限元分析

有限元分析表明，根据框架和核心筒之间的强弱关系，钢-混凝土混合结构体系第1阶屈曲模态可划分为3种，即框架无侧移失稳、整体有侧移失稳和核心筒无侧移失稳，见图4。

图4 钢-混凝土混合结构体系的第1阶屈曲模态

3.1 框架部分可能发生无侧移失稳

选取了5个框架部分可能发生无侧移失稳的钢-混凝土混合结构体系模型A-1～A-5以研究随着支撑所承受的竖向荷载的增大，结构的第1阶屈曲模态变化情况。模型A-1～A-5的几何尺寸相同，各模型总高度为28 m，沿高度均匀设置14根刚性连杆。矩形截面构件的材料为C30，H型和口型截面构件的材料为Q235。

首先，对5个模型中框架和核心筒两部分单独承受竖向荷载时进行屈曲分析，得到了侧向无约束和楼层标高处无侧移2种情况下钢-混凝土混合结构体系的屈曲临界荷载，具体数据见表1。

其次，对5个钢-混凝土混合结构体系的模型A-1～A-5进行屈曲分析，得到了5个模型发生第1阶屈曲时框架和核心筒上承担的竖向荷载qF，qB的相互关系，如图5所示。

设qFs，qBs分别为钢-混凝土混合结构体系中框架和核心筒部分的富余荷载，等于框架和核心筒的有侧移屈曲临界荷载与作用在框架和核心筒上的荷载之差，其可表示为

侧移的框架和核心筒部分单独承受竖向均布荷载时发生无侧移失稳时的第1阶屈曲临界荷载；qBdiv为核心筒部分的屈曲模态转换荷载，

即结构的屈曲模态从框架部分无侧移失稳转变为整体结构有侧移失稳时核心筒部分承担的竖向荷载；qFdiv为框架部分的屈曲模态转换

荷载，即结构的屈曲模态从核心筒部分无侧移失稳转变为整体结构有侧移失稳时框架部分承担的竖向荷载。

（1）qF和qB之间的关系曲线均可分为水平段和斜线段两部分。在水平段与斜线段的交汇点，结构的屈曲模态从框架部分的无侧移失稳变化为整体结构的有侧移失稳。通过研究发现，钢-混凝土混合结构体系屈曲分析得到屈曲模态转换荷载qBdiv与框架和核心筒单独受力时的屈曲临界荷载qFcr，c，qFcr，r，qBcr，c满足如下关系，即endprint

（2）水平段上的点，即当qB≤qBdiv时，结构的第1阶屈曲模态为框架部分的无侧移失稳。图5中5个模型水平段所对应的框架部分所承担的竖向荷载qF与楼层标高处无侧移时框架部分单独承担的竖向屈曲荷载qFcr，r相等，即

（3）斜线段上的点，即当qB>qBdiv时，结构的第1阶屈曲模态为整体有侧移失稳。此时，钢-混凝土混合结构体系第1阶屈曲时所承担的总竖向荷载qcr=qF+qB与框架和核心筒两部分单独承担的竖向荷载时发生有侧移屈曲所承担的竖向荷载qFcr，c，qBcr，c之和相等，即

当qBs>0时，表示钢-混凝土混合结构体系中支撑部分有富余的承载能力，可以为框架提供支撑；当qBs<0时，表示核心筒部分会成为框架的负担，降低框架部分的屈曲时所承担的荷载。

3.2 屈曲模态仅为整体有侧移失稳

选取5个第1阶屈曲模态仅可能为整体结构有侧移失稳的钢-混凝土混合结构体系模型B-1～B-5进行研究，该组几何尺寸和材料与模型A-1～A-5相同。通过对模型B-1～B-5中框架和核心筒两部分单独承受竖向荷载时进行屈曲分析，得到了侧向无约束和楼层标高处无侧移2种情况下结构的屈曲临界荷载，如表2所示。

（1）与图5中的qF和qB关系曲线相比，图6中qF和qB关系曲线仅存在斜线段，结构的第1阶屈曲模态仅可能发生整体结构的有侧移失稳。

（2）5个模型均有qBdiv<0，于是任意点处均有qB>qBdiv，因此结构的第1阶屈曲模态始终为整体有侧移失稳。将图5中各模型对应曲线中的任意点的荷载组合代入式（6）可知，结构屈曲时框架部分所承担的荷载可始终表示为

3.3 核心筒部分可能发生无侧移失稳

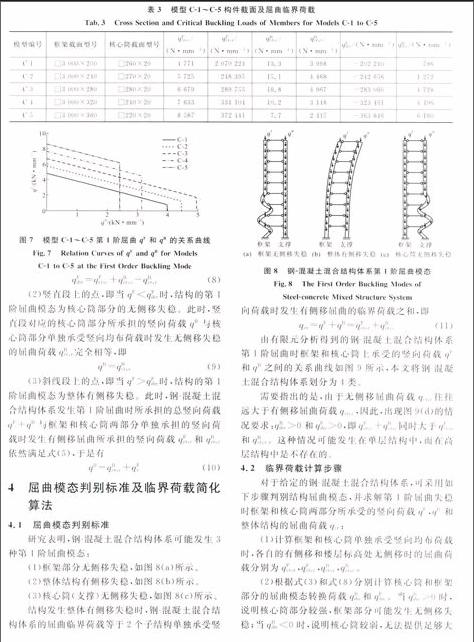
选取了5个核心筒部分可能发生无侧移失稳的钢-混凝土混合结构体系模型C-1～C-5。几何尺寸和材料与模型A-1～A-5相同。通过对模型C-1～C-5中框架和核心筒两部分单独承受竖向荷载时进行屈曲分析，得到了侧向无约束和楼层标高处无侧移2种情况下结构的屈曲临界荷载，如表3所示。

对模型C-1～C-5进行屈曲分析，得到了5个模型发生第1阶屈曲时框架和核心筒上承担的竖向荷载的相互关系，如图7所示。

由图7可知：

（1）qF和qB之间的关系曲线可分为斜线段和竖直段两部分。研究发现，在斜线段和竖直段的交汇点，结构的屈曲模态从整体结构的有侧移失稳变化为核心筒部分的无侧移失稳。此时，屈曲模态转换荷载qFdiv可表示为

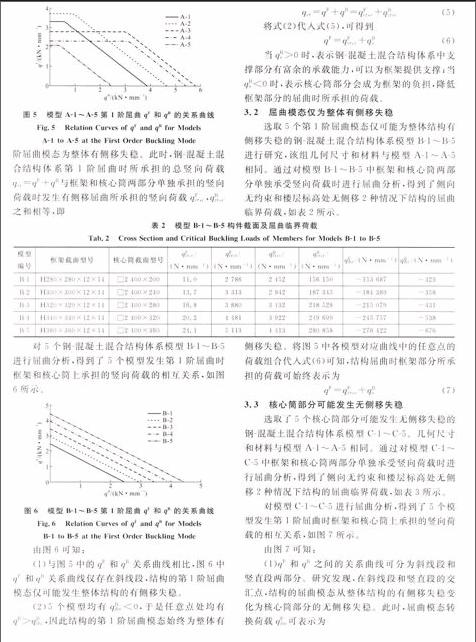
（2）竖直段上的点，即当qF

qB=qBcr，r

（9）

（3）斜线段上的点，即当qF>qFdiv时，结构的第1阶屈曲模态为整体有侧移失稳。此时，钢-混凝土混合结构体系发生第1阶屈曲时所承担的总竖向荷载qF+qB与框架和核心筒两部分单独承担的竖向荷载时发生有侧移屈曲所承担的竖向荷载qFcr，c和qBcr，c依然满足式（5），于是有

（10）4 屈曲模态判别标准及临界荷载简化算法4.1 屈曲模态判别标准

研究表明，钢-混凝土混合结构体系可能发生3种第1阶屈曲模态：

（1）框架部分无侧移失稳，如图8（a）所示。

（2）整体结构有侧移失稳，如图8（b）所示。

（3）核心筒（支撑）无侧移失稳，如图8（c）所示。

结构发生整体有侧移失稳时，钢-混凝土混合结构体系的屈曲临界荷载等于2个子结构单独承受竖向荷载时发生有侧移屈曲的临界荷载之和，即

由有限元分析得到的钢-混凝土混合结构体系第1阶屈曲时框架和核心筒上承受的竖向荷载qF和qB之间的关系曲线如图9所示，本文将钢-混凝土混合结构体系划分为4类。

需要指出的是，由于无侧移屈曲荷载qcr，r往往远大于有侧移屈曲荷载qcr，c，因此，出现图9（d）的情况要求：qBdiv>0和qFdiv>0，即qFcr，c+qBcr，c同时大于qFcr，r和qBcr，r。这种情况可能发生在单层结构中，而在高层结构中是不存在的。

4.2 临界荷载计算步骤

对于给定的钢-混凝土混合结构体系，可采用如下步骤判别结构屈曲模态，并求解第1阶屈曲失稳时框架和核心筒两部分所承受的竖向荷载qF，qB和整体结构的屈曲荷载qcr：

（1）计算框架和核心筒单独承受竖向均布荷载时，各自的有侧移和楼层标高处无侧移时的屈曲荷载分别为qFcr，r，qFcr，c，qBcr，r，qBcr，c。

（2）根据式（3）和式（8）分别计算核心筒和框架部分的屈曲模态转换荷载qBdiv和qFdiv。当qBdiv>0时，说明核心筒部分较强，框架部分可能发生无侧移失稳；当qBdiv<0时，说明核心筒较弱，无法提供足够大的抗侧刚度以使得框架发生无侧移失稳。同理，当qFdiv>0时，说明框架部分较强，核心筒部分可能发生无侧移失稳；当qFdiv<0时，说明框架部分较弱，核心筒部分不可能发生无侧移失稳。

（3）判断结构的屈曲模态。已知竖向荷载qB时，若qB≤qBdiv，则结构的屈曲模态为框架部分的无侧移失稳；若qB>qBdiv，则结构的屈曲模态为整体结构的有侧移失稳。

已知竖向荷载qF时，若qF≤qFdiv，则结构的屈曲模态为核心筒部分的无侧移失稳；若qF>qFdiv，则结构的屈曲模态为整体结构的有侧移失稳。

（4）求解第1阶屈曲时框架和核心筒上所承担的竖向荷载qF，qB。

已知核心筒部分竖向荷载qB时，若屈曲模态为框架部分的无侧移失稳，则qF=qFcr，r；若屈曲模态为整体结构的有侧移失稳，则qF=qFcr，c+qBs（当qBs>0时，核心筒对框架起支撑作用，提高框架部分的临界荷载；当qBs<0时，核心筒将成为框架的负担，会降低框架部分的临界荷载）。

已知框架部分竖向荷载qF时，若屈曲模态为核心筒部分的无侧移失稳，则qB=qBcr，r；若屈曲模态为整体结构有侧移失稳，则qB=qBcr，c+qFs（当qFs>0时，框架对核心筒起支撑作用，提高核心筒部分的临界荷载；当qFs<0时，框架将成为核心筒的负担，会降低核心筒部分的临界荷载）。

（5）求解第1阶屈曲时钢-混凝土混合结构体系的屈曲荷载qcr=qF+qB。

为了便于理解，本文将钢-混凝土混合结构体系第1阶屈曲模态判别标准及临界荷载计算步骤表示为流程图的形式，如图10所示。5 结 语

（1）钢-混凝土混合结构体系的第1阶屈曲模态不仅与框架和核心筒两者之间的截面大小有关，还与框架和核心筒上承担的竖向荷载大小有关。

（2）当核心筒部分的富余荷载qBs>0时，核心筒部分对框架部分起支撑作用；当qBs<0时，核心筒部分反而会成为框架的负担。

（3）钢-混凝土混合结构体系下屈曲模态判别标准能够简便地判断出结构的屈曲模态，针对于各种屈曲模态的临界荷载简化算法计算结果准确、可靠，可供设计人员采用。

参考文献：

References：

[1] CECS 230：2008，高层建筑钢-混凝土混合结构设计规程[S].

CECS 230：2008，Specification for Design of Steel-composite Mixed Structure of Tall Building[S].

[2] LI L，LI G Q，LIU Y S.Simplified Algorithm of the Novel Steel-concrete Mixed Structure Under Lateral Load[J].International Journal of High-rise Buildings，2012，1（4）：247-254.

图10 第1阶屈曲模态临界荷载计算流程

Fig.10 Calculation Flow Chart of the First Order Critical Buckling Load[3] 陆铁坚，许 军.高层钢框架-钢筋混凝土核心筒混合结构破坏过程的数值模拟[J].建筑科学与工程学报，2008，25（1）：32-37.

LU Tie-jian，XU Jun.Numerical Simulation of Failure Process of High-rise Steel Frame-RC Corewall Hybrid Structure[J].Journal of Architecture and Civil Enginneering，2008，25（1）：32-37.

[4]童根树，金 阳，米旭峰.双重弯剪型抗侧力结构的屈曲及其二阶效应[J].工程力学，2008，25（10）：92-98.

TONG Gen-shu，JIN Yang，MI Xu-feng.Buckling and Their Second-order Effect of Dual Systems Consisting of Two Shear-flexural Structures[J].Engineering Mechanics，2008，25（10）：92-98.

[5]童根树.钢结构的平面内稳定[M].北京：中国建筑工业出版社，2005.

TONG Gen-shu.The In-plane Stability of Steel Structure[M].Beijing：China Architecture & Building Press，2005.

[6]王翠坤，田春雨，肖从真.高层建筑中钢-混凝土混合结构的研究及应用进展[J].建筑结构，2011，41（11）：28-33.

WANG Cui-kun，TIAN Chun-yu，XIAO Cong-zhen.Development of Research and Application of Concrete-steel Hybrid High-rise Building Structures[J].Building Structure，2011，41（11）：28-33.

[7]铁摩辛柯S P，盖莱J M.弹性稳定理论[M].2版.张福范，译.北京：科学出版社，1965.

TIMOSHENKO S P，JERE J M.The Theory of Elastic Stability[M].2nd ed.Translated by ZHANG Fu-fan.Beijing：Science Press，1965.

[8]李 亮.多重新型钢-混凝土混合结构设计方法及抗震性能研究[D].上海：同济大学，2011.

LI Liang.Design Approach and Seismic Behavior Study on Novel Multi-lateral Resistant Steel-concrete Mixed Structure[D].Shanghai：Tongji University，2011.

[9]周勇超，李亮亮，李子青.钢-混凝土组合梁界面滑移效应变分法求解[J].长安大学学报：自然科学版，2013，33（1）：39-44.

ZHOU Yong-chao，LI Liang-liang，LI Zi-qing.Solution of Slip Effect of Steel-concrete Composite Beam with Variational Principles[J].Journal of Changan University：Natural Science Edition，2013，33（1）：39-44.

[10] ROSMAN R.Stability and Dynamics of Shear-wall Frame Structure[J].Building Science，1974，9（1）：55-63.endprint