基于人工免疫系统的RBF网络设计

朱亚男

（西安铁路职业技术学院 牵引动力系，陕西 西安 710014）

径向基函数（Radial-Basis Function，RBF）神经网络（RBF网络）是一种典型的局部逼近网络模型[1-2]。与其他类型的神经网络相比，RBF网络不仅具有较强的生理学基础，而且其结构简单，在学习速度、逼近性能等方面更具优势。

RBF网络常用的学习方法[3-6]有：随机选取中心法、正交最小二乘法（OLS法）、自组织选取中心法以及有监督地选择中心法。但这些方法都不能完全通过学习的方式得到全部的RBF网络参数，其中部分参数是靠经验预先设计的：如随机选取中心法、自组织选取中心法以及有监督地选择中心法，需要预设网络中心点的数目；而OLS法则需要预设网络的扩展常数。此外，除有监督地选择中心法外，其他学习方法都主要训练网络中心这个参数，对网络扩展常数的训练则比较忽略，而扩展常数恰恰是决定RBF网络性能至关重要的因素，其值过大或过小都会严重影响RBF网络的性能。除上述常用学习方法之外，其他一些基于进化算法的RBF网络学习策略，也大多存在类似问题，且往往会导致算法过于复杂、训练时间过长且容易陷入局部极小等问题。

鉴于上述问题和不足，本文提出一种基于免疫机制的RBF网络设计与学习策略，RBF网络的所有参数都能通过训练得到全局最优值，同时为了简化网络训练过程，该方法特地引入人工免疫系统特有的疫苗抽取与接种机理，从而进一步优化了网络性能。

1 RBF网络学习策略结构设计

RBF网络结构如图1所示，表示具有n维输入、h个隐节点、m 维输出的 RBF 网络结构模型。 其中，x=[x1，x2，…，xn]T∈Rn×N为网络的输入向量，N 为样本数目；φi（i=1，…，h）为隐层节点的径向基函数，w∈Rn×m为输出权矩阵，b1， …，bm∈Rm为输出单元偏置值，y=[y1，y2，…，ym]T∈Rn×m为网络输出，∑表示y是隐节点输出的线性加权。

其中 φ（·）一般为高斯函数，形如式（1）：

式（1）中，ci为基函数的中心，决定了基函数的位置；σi为扩展常数，决定了基函数的宽度；通常取为欧几里得距离。

图1 径向基函数（RBF）网络结构Fig.1 Radial basis function （RBF）network structure

由式（1）可看出，当 RBF 网络的 h、ci、σi（i=1，2，…，h）唯一确定后，则网络隐层的径向基函数就确定了，即确定了输入空间到隐层空间的映射关系；当wi和b唯一确定后，隐层空间到输出空间的线性映射关系也可确定。RBF网络的设计和训练主要目的就是确定上述参数。而上述参数全部在同一个优化空间同时得到是不必要且极为影响效率的：优先确定参数h就决定了整个RBF网络的拓扑结构，可大大简化网络训练过程；然后只要确定了参数，就可构建合理的网络隐层，进而就能够通过线性优化的方法确定输出层参数{wi，b}。

基于上述分析，本文提出RBF网络三级学习结构策略：将构成RBF网络的参数空间Θ分解成为三个子空间：Θ1={h}，Θ2={ci，σi}和 Θ3={wi，b}，然后对这三个子空间分别进行优化设计。图2为网络的学习结构框架，由图2可看出该框架分为三级结构：第一级计算Θ1（抽取疫苗）；第二级经疫苗注射后用免疫算法设计确定Θ2；第三级采用最小二乘估计Θ3。经三级学习后就确定了 RBF网络参数空间 Θ3={Θ1，Θ2，Θ3}，即构造出了完整的RBF网络。

图2 RBF网络三级学习结构Fig.2 Athree－level RBF network learning structure

2 基于人工免疫的RBF网络实现

上述RBF网络三级学习结构，其每一级具体实现过程如下：

第一级：获取疫苗，得到网络结构。

第一级计算Θ1={h}，直接决定了RBF网络隐层神经元的个数，是该学习方法中的疫苗，同时也是形成网络拓扑结构的重要步骤。令k以1为步长在节点数目的允许范围内搜索，即k=1:1:Maxh，Maxh为网络允许的隐层最大节点数，1为最小节点数，同时搜索过程中k个数据中心{c1，c2，…，ck}是在输入样本 x∈Rn×N中随机选取的，满足式（2）：

式（2）中，Round（·）为取整函数，rand 为区间[0，1]内的均匀随机数，n为输入数据维数。确定数据中心后，按式（3）选择扩展常数σ。

此后，采用伪逆阵法确定网络输出层线性参数：

Gw+b=p⇒[w，b]=[G，I′N]+×p（w∈Rk×m，b∈Rm⇒[w，b]∈R（k+1）×m

G∈RN×k，I′N∈RN×1⇒[G，I′N]∈RN×（k+1），p∈RN×m）（4）

式（4）中，p∈RN×m为N个训练数据集的m维期望响应矢量；[G，I′N]表示矩阵[G，I′N]的伪逆阵[G，I′N]，其中I′N∈RN×1为元素为1的N维列向量，G∈RN×k定义为：

式（5）中，xj是输入训练数据集的第j个输入矢量，N是训练样本数目。

根据式（2）～式（5）可构建出第一级的RBF网络，在 k=1:Maxh的搜索过程中，k取值不同时网络所表现出的输出误差ε也不同，当误差ε≤με时（με为指定的误差上限），k值即为该级提取的疫苗，即该RBF网络的隐层节点数h。

第一级输出为h，h=k。

第二级：经注射第一级结构提取的疫苗后再构建RBF网络隐层。

第二级注射疫苗h即确定了网络的拓扑结构，在此基础上通过学习确定参数子空间Θ2={ci，σi}。该级采用基于实数编码的免疫克隆选择算法ICSA[7]。具体如下：

1）抗原：需利用当前构建的RBF网络去求解的目标函数。

2）抗体：抗体形式为 ai=[c，σ]，与 RBF网络隐层参数相对应，其中 c=（c1，c2，…，ch）为数据中心，σ=（σ1，σ2，…，σh）为扩展常数。 抗体群 A={a1，a2，…，aM}，M 为群规模。 抗体采用实数编码。

初始化抗体群矢量c和σ矢量均随机产生，分别见式（6）和式（7）：

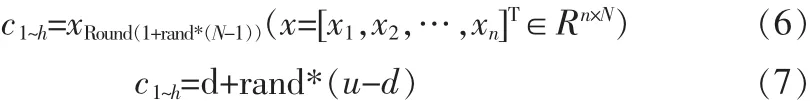
3）抗体－抗原亲合力：选择当前RBF网络的输出误差函数评价，即式（8）：

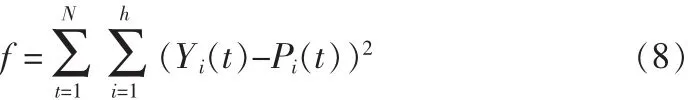
式（8）中，Yi（t）和 Pi（t）分别是第 t个输入模式中第 i个节点的实际输出和期望输出，N和h分别为输入样本数目和隐层节点数。

4）克隆选择：新一代抗体群用克隆选择算子操作产生，依据变异概率pm对克隆后的子抗体群进行变异操作，针对抗体中代表中心的矢量c和代表扩展常数的矢量σ分别按式（9）和式（10）进行变异；评价克隆变异后的子抗体群的亲合力进行选择，保留下来的抗体是亲合力最小的，也就是网络隐层输出误差最小的最优值。

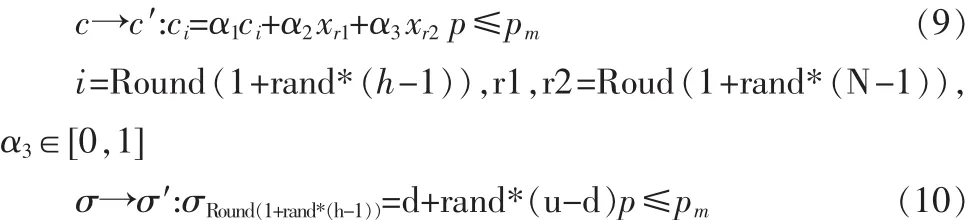
第二级输出为 ci和 σi。

第三级：在第一级和第二级结构得到的参数子空间Θ1和 Θ2的基础上，构建参数子空间 Θ3={wi，b}，即确定 RBF网络输出层。采用最小二乘法，见矩阵方程式（11）：

Gw+b=p （11）

图3为以上所述RBF网络三级学习算法流程图，其中的停止条件为达到最大世代数或达到要求的误差标准。

图3 基于免疫机制的RBF网络三级学习算法流程Fig.3 The three-level RBF network learning algorithm flow chart based on immune system

3 仿真实验

为检验算法性能，进行Hermit多项式逼近实验，为在实验中有对比性，用上节提出的学习方法（以下简称免疫三级算法）和传统训练方法中较为常用的梯度算法分别训练RBF网络进行实验。Hermit多项式为式（12）：

实验中两种网络学习算法的训练、测试样本均相同。训练样本的输入为区间[-4，4]内的随机分布序列，样本的输出为 h（xi）+ei（ei∈N（0，1）为服从标准正态分布的噪声），训练样本数N=100。图4为目标函数和训练样本分布图。

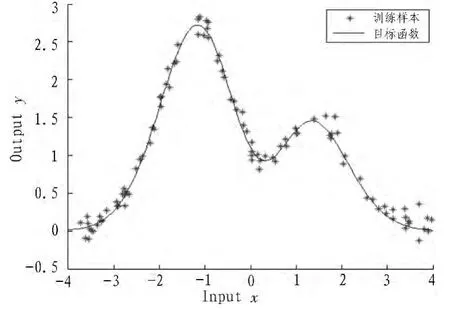
图4 目标函数和训练样本Fig.4 The objective function and the training sample

测试样本的输入为区间[-4，4]内的均匀分布序列，输出则为输入代入Hermit多项式的对应生成值。测试样本数为NT=101，将梯度算法的隐层节点数设为10，代入训练样本用两种算法分别训练RBF网络。图5为两种方法训练的RBF网络分别代入测试样本的输出对比。

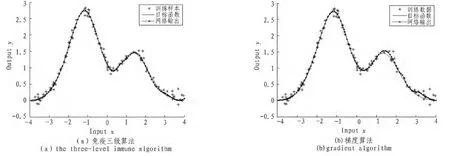
图5 两种学习算法训练RBF网络的测试输出Fig.5 Test output of two learning algorithms trained by RBF network

图6 为两种RBF网络的输出与实际输出的误差对比。免疫三级算法训练最终得到的网络测试误差为SSE=0.072 7；梯度算法的网络测试误差则为SSE=0.167 2。

由上可知，经免疫三级算法训练的网络较普遍采用的梯度算法训练的网络精度更高。同时梯度算法还需要凭经验预设网络的隐层节点数h，经验不足设定偏差会影响整个网络性能，而免疫三级算法在自身学习过程中就能够得到网络隐层节点数的最优解作为疫苗，参数确定过程没有预设因素，因此更加科学。图7所示为免疫三级算法的学习过程。

由图7（a）可看出免疫三级算法在第一级得到的输出结果为，说明实验结果是由9个位于不同位置且宽度不同的隐层基函数曲线经加权输出得到的。算法训练的具体基函数曲线以及加权结果参见图8。

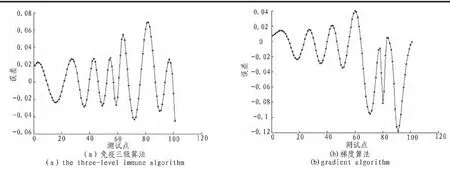
图6 两种学习算法训练RBF网络的测试误差Fig.6 Test error of two learning algorithms trained by RBF network

图7 免疫三级算法学习过程Fig.7 The learning process of the three-level immune algorithm

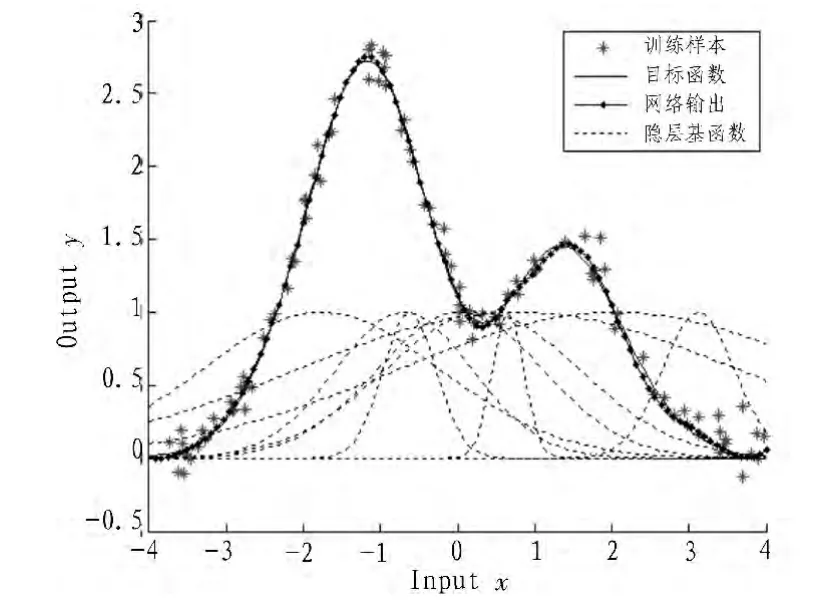
图8 免疫三级算法训练RBF网络隐层基函数加权输出Fig.8 RBF hidden layer basis functionsweighted output trained by the three-level immune algorithm

4 结束语

本文提出的免疫三级算法可经过训练得到全局最优的RBF网络所有参数空间，将RBF网络参数空间Θ分解为Θ1={h}、Θ2={ci，σi} 和 Θ3={wi，b}3 个子空间， 采用三级结构分级学习，从而简化了参数空间的寻优过程。在第一级获取疫苗，不仅确立了RBF网络的拓扑结构，同时也降低了第二级结构中搜索空间的复杂度；第二级采用先进的人工免疫算法进行多点搜索，从而找到全局最优解；第三级则采用最小二乘法，简便易行，同时也降低了第二级结构的维数，提高了算法效率。

由典型的逼近实验测试性能可知，免疫三级算法较常见的梯度算法训练的网络测试精度更高，算法性能更优越，因此有非常大的应用价值。

[1]Powell M J．Radial basis function for multivariate interpolation[R]．England：Cambridge University，1985．

[2]Hush D R，Horne B G．Progress in supervised neural networks[J]．IEEE Signal Progressing Magazine，1993（1）:8-39．

[3]Broomhead DS，Lowe D．Multi-variable functional interpolation andadaptivenetworks[J]．ComplexSystem，1988，2（2）:321-355．

[4]Chen S，Cowan C F N，Grant PM．Orthogonal least squares learning algorithm for radial basis function networks[J]．IEEE Transactions on Neural Networks，1991，2（2）:302-309.

[5]Moody JE，Darken C J．Fast learning in networks of locallytuned processing units[J]．Neural Computation，1989，1（2）:281-294．

[6]Karayiannis N B．Reformulated radial basis neural networks trained by gradient descent[J]．IEEE Transactions On Neural Networks，1999，10（3）:657-671．

[7]焦李成，杜海峰，刘芳，等．免疫优化计算、学习与识别[M]．北京：科学出版社，2006．