六自由度平面双足机器人的步态规划

李 彬，李界家

（沈阳建筑大学 机械工程学院，辽宁 沈阳 110168）

0 引言

双足机器人具有多关节连接的腿部结构，相比轮式、履带式机器人就能很容易的越过较高的障碍物，双足机器人对行走的地形环境要求更低，效率很高。这些显著的优势使双足机器人在军事领域、地形探测和、抗震救灾这些复杂多变的环境下，能够在短时间内完成各种复杂的动作，从而达到所规定的任务指标。所以对双足机器人的步态规划研究具有很大的潜在价值。

双足步态的实现需要解决非常复杂的控制难题。双足系统不仅是非线性的，而且对于开环和闭环模型都是不连续的而且还受地面约束。本文对六自由度双足机器人进行正逆运动学分析，基于三次样条差值对双足机器人的步态进行合理规划。

1 双足步行机器人运动学建模

由于双足机器人具有复杂的运动学、动力学和控制特性，我们需要提取机器人的具体特征进行建模，这样一来可以有效的降低步态规划和步行控制的难度，从而实现稳定的步行和控制。

建立运动学方程我们需要建立坐标变换方程，把一系列的坐标系建立在连接连杆的关节上，这些坐标之间的相对位置和方向用齐次坐标变换来描述，就可以建立起机器人的运动学方程。但我们需要解决的问题是如何在每个关节上确定坐标系的方向、如何确定相邻两个坐标系之间的相对平移和旋转量，因此需要采用一种合适的方法来描述相邻连杆之间的坐标方向和参数。在这里我们运用D－H 参数法。根据运动学模型列出D－H 参数表1。

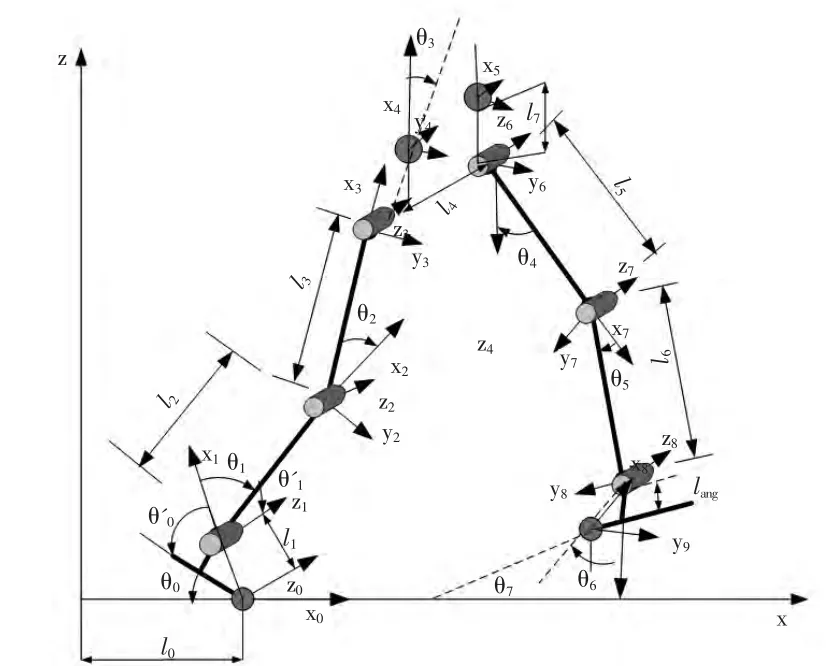
图1 双足机器人参考坐标系Fig.1 The reference frame of a biped robot

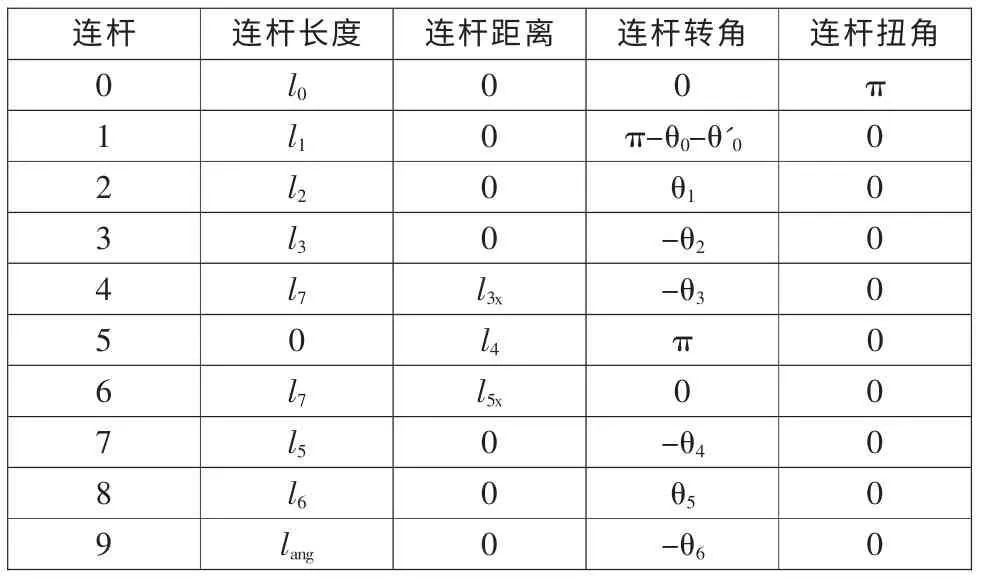
表1 双足机器人运动学参数表Tab.1D-HParametersforbipedrobot

1.1 正运动学建模

根据上述D－H 法则的坐标变换规则，各个坐标之前的齐次变换表示：

根据以上矩阵，对于此双足机器人来讲，如果各个关节角度给定我们可以通过正运动学模型来确定其具体的位置和方向。齐次变换矩阵从坐标i 到坐标j 可以通过，i＜j 得到。用xiyizi分别表示坐标系i 对应坐标系r 的轴xyz。根据齐次坐标变换矩阵的定义得到各个坐标值的部分表达式如下：

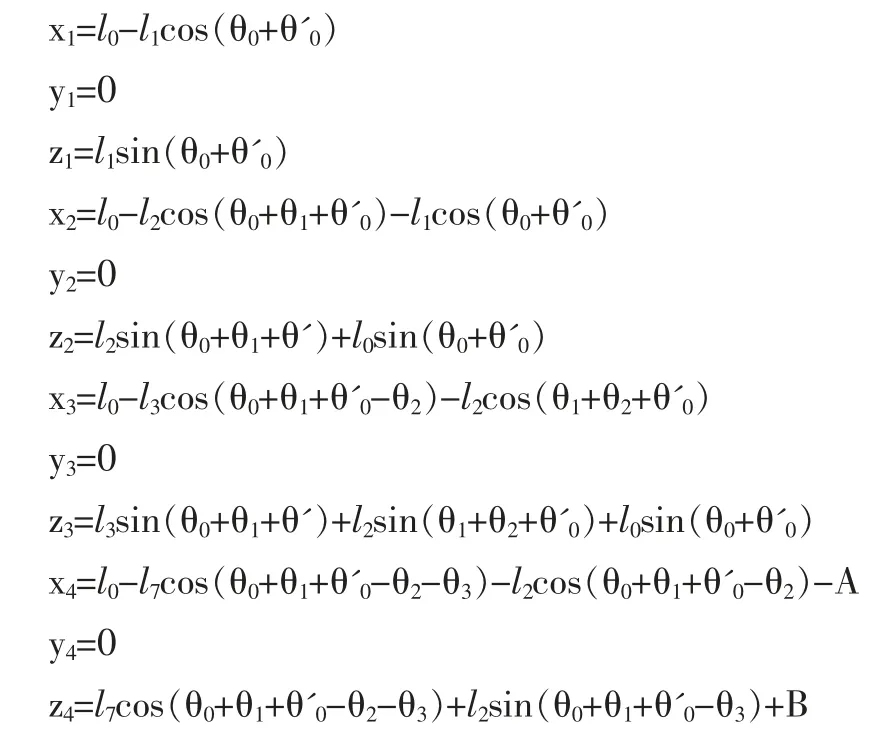
其中：

1.2 逆运动学分析

逆运动学解决的问题是根据关节位置求出关节角度，根据机器人的几何约束，求解机器人的膝关节、髋关节等受约束的关节角。注意到右脚踝和左脚踝分别用由坐标（x1，y1，z1），（x8，y8，z8）和转动角度θ0和θ7来确定。这里使机器人便于直立行走，上肢和竖直平面常常设置为0。考虑到双足机器人的机械结构特点其表达式：

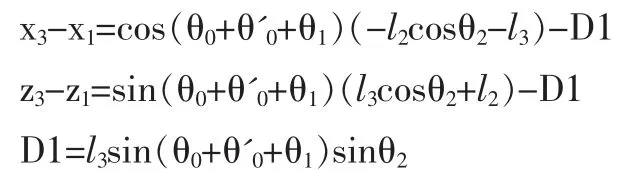
由－θ0+θ'1+θ2+θ3=0 可以得到θ3的值。又由于两腿的对称性，根据上式可得到：

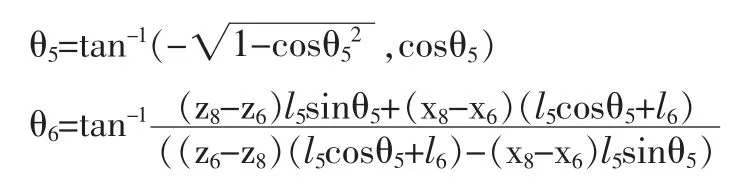
为了方便计算我们进行如下符号替换：

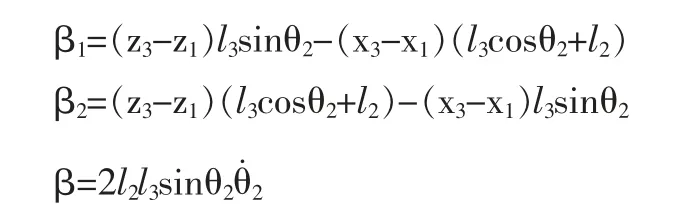
我们可以对上述写成：

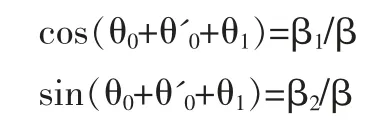
根据求导上式得到：

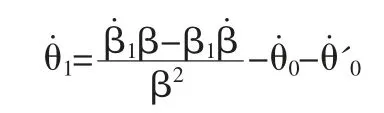
我们先进行下列定义：

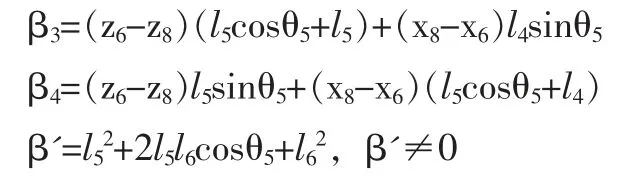
由于两条腿的对称性，同理得到右腿关的表达式：

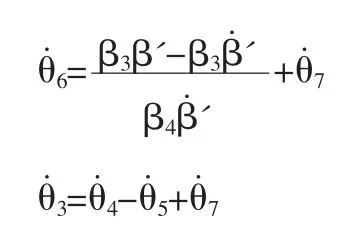
这样我们就可以通过预设关节角度和步态规划，得到准确的转动角度。

2 双足步行机器人的步态规划

仿人双足机器人是集移动功能,操作作业功能以及人际交互功能与一体的多功能机器人。要实现仿人双足机器人在人类所处的环境下独立工作或者协助人类工作，从机械结构的观点来看，双足机器人本身就是不稳定的，因为在行走的大部分时期重心是在脚支撑区域以外的。对于双足机器人来说稳定性可以分为两种：第一种为外在干扰下每个步行阶段都需要动力结构的稳定，这意味着，在支撑阶段机器人可以保持稳定的姿态。另一种是机器人需要步态稳定，这说明的是可以通过合适的步态规划和调整使双足机器人在复杂的环境中稳定连续的行走。这里说的稳定性是指双足机器人可以持续保持预设期望的步态而不摔倒。

2.1 步态的选择

步态规划要模仿人类的行走特点，再根据机器人特有的结构进行，常用的步态有下列几种：

第一种步态如图2（a）所示，双脚支撑期和单脚支撑期之间是紧接着出现的，摆动脚在离开和接触地面时都是和地面平行，但由于具有主动驱动的关节，我们完全可以通过转动允许的关节角度使ZMP 保持在支撑脚与地面接触的区域。我们可以认为这种步态在双脚支撑期的初始阶段由于是整个脚掌同时着地可能会不稳定。

第二种步态如图2（b）所示，是在第一种基础上，加上了摆动脚的关节角度，摆动脚离开和接触地面时都有特定的角度，脚跟先着地然后是整个脚掌，后脚跟抬起，下一步落地时，后脚跟先着地，等到全部着地的同时，支撑脚的后脚跟抬起。大多研究表明这种步态符合人类自然性走步态对提高稳定性有很大的帮助。

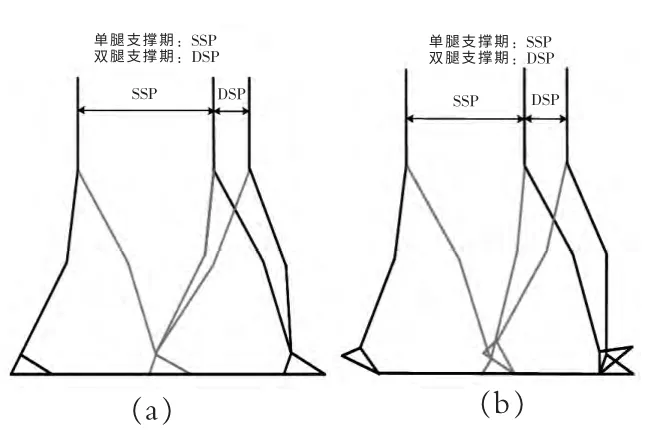
图2 步态模式类型Fig.2 Types of walking patterns

第三种步态如图3 所示，第三种步态考虑到双足机器人与人类结构上的差别，在单腿支撑期和双腿支撑期之间加入一个过度子阶段，在第一个过度子阶段，后脚从抬起，摆动到完全落地，支撑脚不动，等完全落地后支撑脚才变为摆动脚，以这样的方式周期性运动。增加了稳定性。

由于本研究中的机器人属于平面双足步行机器人，脚踝在侧向平面内不做左右转动，所以双脚在y 方向的坐标是定值。我们可以用三个参数来表示脚的轨迹，左脚：（xla（t），zla（t），θla（t）），右脚（xra（t），zra（t），θra（t））。其中x 和z 代表的是坐标值；θ 代表脚在离开和接触地面时都有特定的角度。

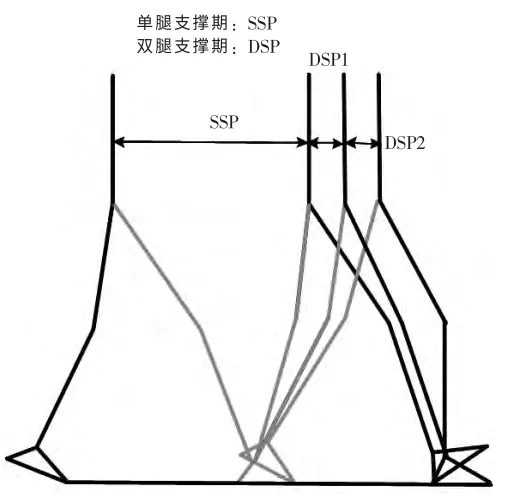
图3 步态模式优化图Fig 3 The optimized Types of walking patterns

2.2 踝关节轨迹规划

根据第三种步态的特性和步行的周期性我们可以这样完整的描述一个周期的步行过程：假设奇数步从右脚的离地开始到右脚第一次与地面接触结束，与此同时偶数步从左脚离开地面开始到左脚与地面接触后结束。用T 表示步行周期，D 表示步长，设N 代表步数，用Td表示单腿支撑的时间，如图所示：第N 步开始于双腿支撑期，此时左脚作为之前的摆动脚刚好完全与地面接触，此时右脚后脚跟正要向上抬起直到达到与地面夹角θ 后离开地面在t=（T+Td）/2 时脚开始摆动, 在这里假设摆动脚在t=NT+（Td+Ts）/2 时达到轨迹的最高点，t=T+Ts时单腿支撑阶段结（以双脚支撑期开始）在这里假设摆动脚在t=NT+（Td+Ts）/2 时达到轨迹的最高点，在t=T+Ts时单腿支撑阶段结束且右脚后脚跟以角度θ 与地面接触，然后逐步全部接触，这一过程左脚始终与地面接触，完成了一个步行周期。之后进入下一个步行周期的双脚支撑阶段的中间阶段。此时t=（N+1）T 步时过程是一样的只是左右脚的动作互换。根据上述分析，摆动脚的转角方程如下：

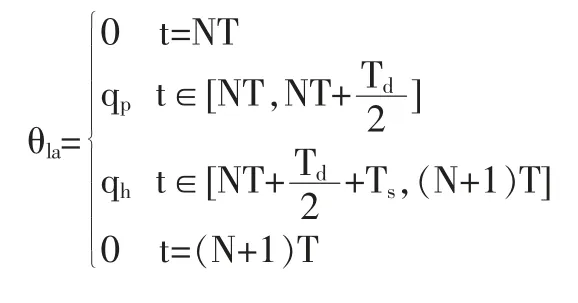
摆动脚垂直方向的轨迹方程：

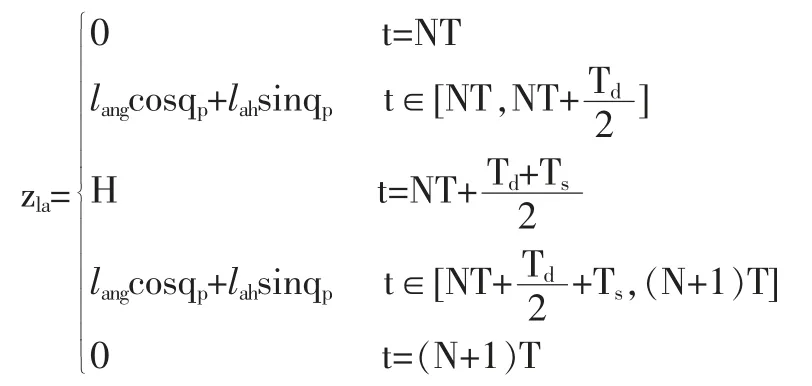
摆动脚的水平轨迹方程：

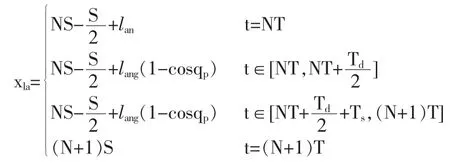
在步行周期开始时也是上一个步行周期结束时，要实现平稳过渡此时的摆动叫转动的角加速度为零，而且由于右脚脚底作为支撑脚相对于地面是静止不动的，所以应该满足下列条件：

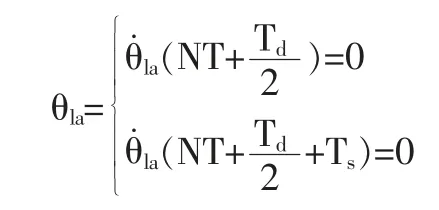
前向和纵向平面内的抬脚和落脚点的速度最低为0，可以是震动和冲击力减小到最小，我们使其一阶导数为零。

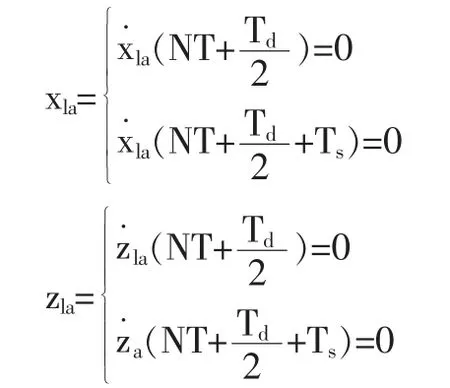
为了生成一条光滑的轨迹，必须满足一阶导数时可微的和二阶导数时连续的，再把上述的约束条件带入固定边界求出系数矩阵，在将踝关节各个关键时刻的位置、角度带入插值函数就可以生成右脚的轨迹。最后我们可以根据调节角度、抬脚高度等生成不同的脚踝轨迹。

2.3 髋关节轨迹规划

同踝关节规划一样，因为是平面双足步行机器人，髋关节只会绕y 方向进行转动，左右髋关节在y 方向的坐标值保持固定不变。髋关节的双足结构特点且受地形的制约，在水平地面上行走最理想的状况是使躯干与地面保持垂直，方便起见、使髋关节轨迹保持成一条水平的直线。这样做的目的也是避免重心在竖直方向摆动幅度太大造成机器人的不稳定性。我们设为髋关节在z 方向为定值。

我们用Xs 表示在单腿支撑期开始时髋关节到支撑脚的踝关节在X 方向的距离、用Xe表示在单腿支撑期结束时髋关节到支撑脚的踝关节在X 方向的距离，我们可以设定X 方向的约束条件：

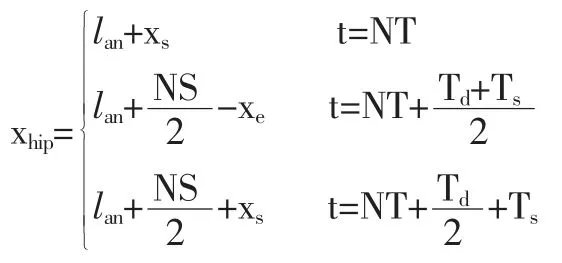
因为单脚支撑期相对于双脚支撑期的不稳定性，我们可以让髋关节在双脚支撑期间进行快移动，而在单脚支撑期相对进行较慢移动。注意到Xs，Xe对于步行机器人的稳定性重要的参数，根据参考文献[2]提出了允许的最大稳定范围，在这里我们设髋关节和踝关节之间0.5 个步长。

2.4 步态仿真实验

如上分析双足机器人的轨迹由两部分组成，脚踝轨迹和髋关节，知道了这两个轨迹我们就可以通过逆运动学确定所有关节的轨迹。通过上述轨迹计算并在Matlab中仿真进行演示结果如下，其中步态仿真的图4 中，其后脚跟和前脚与地面接触最大30°，而步态仿真的图5 中是60°。

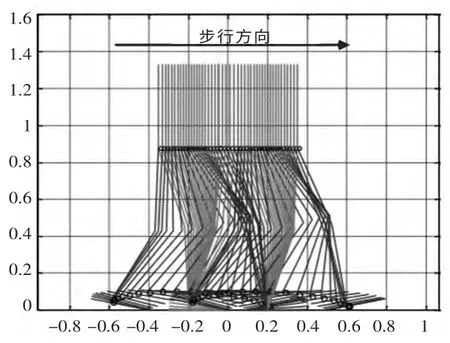
图4 步态仿真图Fig.4 Gait simulation

3 结论

本文通过运动学建模，然后运用逆运动学的求解，最后基于三次样条线性差值完成了双足机器人的步态规划。考虑到单脚支撑到双脚支撑的光滑过度的重要性，设计了合适的步模式，最后通过仿真实验进行了验证。

[1]Gouwanda D, Senanayake S, Marasinghe M, etal. Real time force sensing mat for human gait analysis[J]. World Acad. Sci. Eng. Technol, 2008，15.

[2]A.Goswami,Postural Stability of Biped Robots and the Foot-Rotation Indicator (FR1) Point, The International Journal of Robotics Research，18，6，pp.523-533，1999.

[3]李国栋，李光日同，田玉敏.一种用于测量机器人ZMP 的多点压力传感器[J].微计算机信息，2010，17.

[4]Shuuji Kajita，Hirohisa Hirukawa,Kensuke Harada, Introductiont to Humanoid Robotics.

[6]Q.Huang and S.Kajita.Planning Walking Patterns for a Biped Robot，IEEE Transactions on Robotics and Automation,Vol.17，No.3，200.