基于最优控制的移动机器人轨迹运动研究

向昱丞，柳 波

（1.中国兵器工业第五八研究所 特种电子技术部，四川 绵阳 621000；2.绵阳师范学院 数学与计算机科学学院，四川 绵阳 621000）

0 引言

自主式移动机器人正日益应用到工业、科研项目和其他许多人类不可能直接介入的领域。移动机器人的控制问题与多年来广泛的实际应用密切相关。近年来已经有大量的关于移动机器人控制的研究工作在开展。

轨迹控制的任务主要是尽量减少移动机器人实际位置，对参考轨迹所指定位置的偏离。简化的非线性模型作为一种控制方法，仅仅描述了机器人当前运动参数与参考轨迹预定参数的运动学关系，一般的研究方法主要有两种：一是基于参考轨迹的线性化控制设计，通常使用极点配置调整控制器参数；二是基于反馈线性或非线性控制设计方法。

尽管这些方法具有一定效果，但针对轨迹控制系统的研究，最优控制法的效果更好。一些研究中也提出采用设定参数控制法解决一些优化问题，其跟踪质量取决于设定的参数，要想得到好的控制效果，其设定的参数必须是优化的。其结果是导致得出的控制律由选取的参数所决定。

本文主要研究了基于最优控制的移动机器人轨迹运动系统的合成。该问题的解决以最优控制和奇异摄动法为基础。文中对所研究的问题进行了降阶处理，并对控制器进行了简化，最终给出了其控制律的实现。

1 轨迹控制

1.1 移动机器人的数学模型

图1 显示了移动机器人在平面中的运动，式（1）为其运动学模型：

图1 平面上移动机器人的运动Fig.1 Motion of mobile robot on the plane

式中：X，Y 为移动机器人在平面中的当前坐标；V1，V2，V 分别为左右履带及机器人的线速度；ω—机器人的角速度；φ—向量与轴的夹角。

假设两个电机完全相同，移动机器人在水平面运动的动力学方程如下[1，2]：

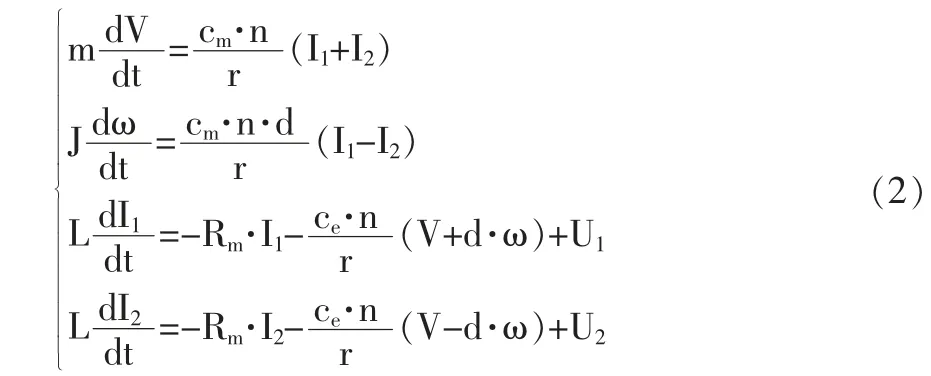
其中m，J 分别为机器人的质量和惯性力矩；n—齿轮比；r—驱动轮半径；cm—电机的转矩常数；I1，I2—电机的电枢绕组中的电流；U1，U2—电机的电枢电压；Rm，L 分别为电机中电枢绕组的电阻和电感；ce—电机电动势常数。

1.2 移动机器人的运动轨迹控制

假设给定的轨迹如下：pref（t）=（Xref（t），Yref（t），φref（t））。图2 是对移动机器人轨迹追踪误差[3～7]的描述：

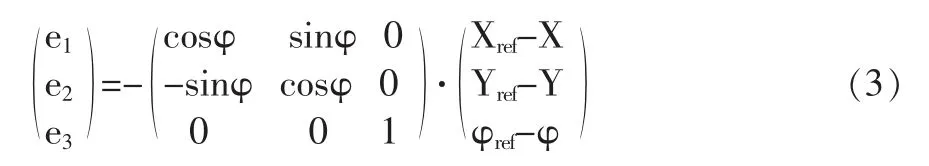
对式（3）求微分，我们可以得到参考轨迹下移动机器人追踪误差的非线性模型。方程组线性化后得：

其中u1=Vref－V，u2=ωref－ω。现在的问题是寻求输入信号u1，u2根据最优控制理论，它们可以通过积分二次型性能指标函数的最小值获得：

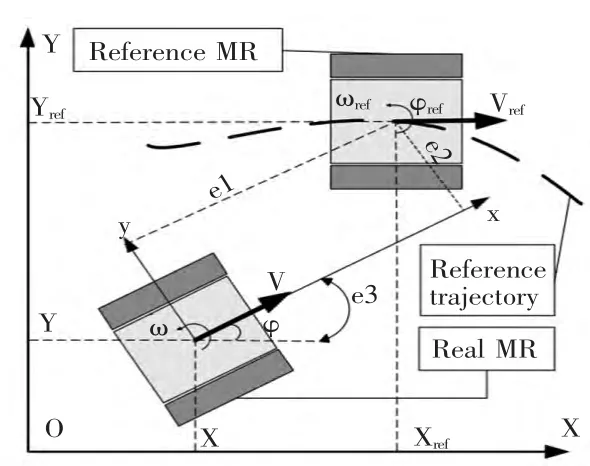
图2 移动机器人轨迹运动控制Fig.2 Trajectory motion control ofmobile robot

已知控制输入u1，u2，机器人的期望速度计算：Vreq=Vrefu1，ωreq=ωref－u2。接下来需要将机器人的线速度和角速度稳定在期望值Vreq和ωreq附近，这可以转化为最优控制问题，如系统运动轨迹的二次型性能指标函数：

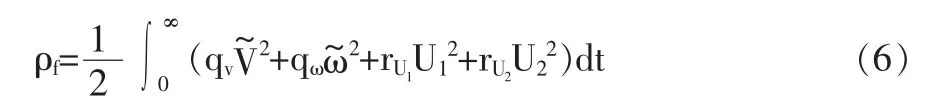
2 轨迹控制问题的解

2.1 位置控制环的合成

基于系统（4）、（5）的最优解的位置控制环的设计，可以写成以下形式：

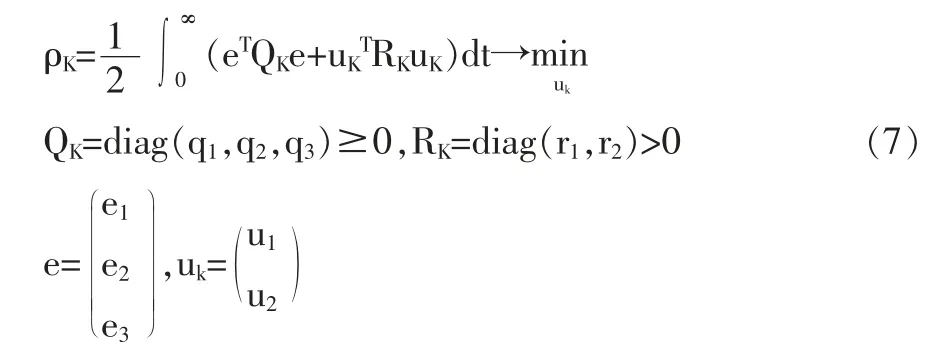
约束条件为：

为简化起见，忽略时间依懒性，式（7）、（8）在能控矩阵对（A（t），B）（适用于所有Vref和ωref不为零的情况）下的解[8]为：这里的PK为Riccati 矩阵差分方程的一个对称正定解，满足：0。则移动机器人线速度和角速度的期望值为：Vreq=Vrefg11e1－g12e2－g13e3；ωreq=ωref－g21e1－g22e2－g23e3。

2.2 速度控制环的合成

速度控制环合成的任务，我们表述为以下形式：

约束条件为：

如果系统（10）是可控可观测的，则系统（9）、（10）的最优控制问题有唯一的解[9]：

其中P 为Riccati 矩阵代数方程的一个解，满足：0=-ATP-PAT+PBTR-1BP-Q。该解的主要缺点是：一方面对Riccati 矩阵方程进行实时求解是很困难的；另一方面要求测量用于评估控制效果的状态向量的所有组件，这对控制策略（11）的使用带来更大的限制。因为通常机器人装备有电机角速度传感器，但不是电流传感器。假设我们测得移动机器人电机的角速度ωr1和ωr2，由式（1）容易得到：

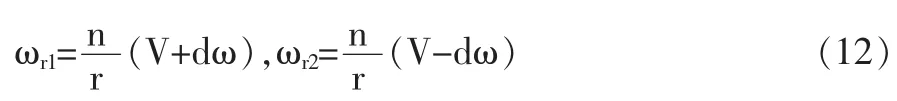
可用以下输出方程对状态空间方程（10）加以补充：

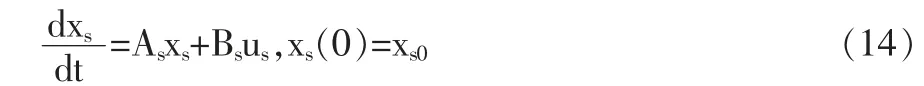
由于无穷小量ε 和赫尔维茨矩阵A22，式（11）和（15）的解渐进相等[8]。

由系统式（13）有：xs=C1-1y。代入式（11）和（16）得：

式（15）～（17）是移动机器人速度控制次优问题的数学基础，对衰减问题的解决是必不可少的。在快慢子系统稳定的情况下，区间（0，ε*）内原始闭环系统是稳定的。临界值ε*是原始闭环系统鲁棒性的一个重要指标，ε*值越大，系统鲁棒性就越好。

3 轨迹运动控制系统的结构

将控制问题分解成位置控制和速度控制两个子问题，形成了如图3 所示的轨迹控制的系统结构。系统主要包括两个部分：参考模块和执行模块。参考模块位于PC 端，它由轨迹发生器、位置控制环和误差计算单元组成。执行单元置于移动机器人主板上，包括速度控制环和位置估计单元。

3.1 移动机器人轨迹发生器

用平面内任意点M表示移动机器人，其将沿着参考坐标Xref，Yref形成的参考轨迹行进。M 点的速度可以用以下连续时间函数进行估计：

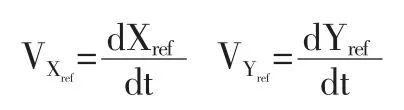
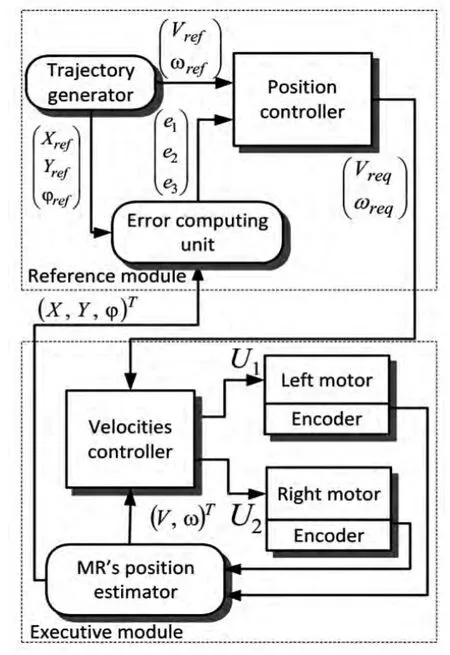
图3 移动机器人控制系统结构图Fig.3 Mobile robot control system structure diagram

由于移动机器人是一个非完整约束系统，因此存在一个如下形式的非完整约束[11]：-VXsinφ+VYcosφ=0。此约束不允许任意设置机器人的角坐标φ，其必然是以下微分方程的一个解[11]

其中bMcosγ 和bMsinγ 为与机器人相关的坐标系统中M 点的常数坐标。对式（18）进行积分，可以得到φref的变化规律。

3.2 移动机器人的位置估计

通过测量电机的角速度ωr1和ωr2，可以对移动机器人的当前位置进行估计。根据式（12），可以得到其线速度和角速度：。根据式（1），由欧拉近似方程可得移动机器人的当前位置：

其中，Ts为采样周期，下标p 匹配最后一个采样点的对应值。

4 控制系统的实验测试

4.1 系统结构及参数

图4 为所设计的履带式移动机器人。机器人参数：履带长l=0.245m，驱动轮半径r=0.03m，质量m=0.83kg，中心到履带的距离为d=0.19m。

电机参数：额定电压UH=7.2V，电枢电阻Rm=100Ω，电枢电感L =0.0123H，齿轮比n=86.8。用两个正交编码器测量电机转速。

4.2 实验过程及结果

图4 履带式移动机器人Fig.4 Tracked mobile robot

作一个圆作为测试轨迹。初始时刻，移动机器人处于点（0，0），轨迹从点（0，0.25）开始移动。谐波信号Xref（t）和Yref（t）频率的设置为可使得参考轨迹pref（t）形成40 秒一圈。

实验结果显示系统具有较好性能。机器人进入参考轨迹持续8 秒，偏差为｜eX｜≤0.22m，｜eY｜≤0.008m，｜eφ｜≤0.05rad，相对轨迹追踪误差不超过9%。

5 结论

本文研究了履带式移动机器人轨迹运动最优控制问题。系统包括了两个模块（参考模块与执行模块）和两个回路（位置控制环与速度控制环）。通过对描述追踪误差的线性二次型优化问题的求解，实现了轨迹控制回路的合成。其数学模型为移动机器人参考轨迹的跟踪误差动态系统的切线线性化，一般情况下，其控制律是一种时变系数的跟踪误差反馈。机器人线速度和角速度的时变性决定了系统的非稳定性质。如果线速度和角速度速度恒定不变，系统将变得稳定。

移动机器人的速度（线速度和角速度）控制环的设计也是同样基于了对线性二次型优化问题的解决。为了简化此问题，从计算和最优控制律实施的角度出发，使用奇异摄动法得到其渐近逼近。

通过研制的履带式机器人对轨迹运动控制系统进行实验验证。实验结果表明该控制系统对控制目标具有较好的控制效果。

[1]A. A. Kabanov, Suboptimal Robust System for Mobile Robot Motion Control[J]. Mechatronics, Automation, Control，2013，4.

[2]H. Kvakernaak，Linear optimal control systems，John Wiley & Son Inc[M]. New York, 1972.

[3]W.E.Dixon，Nonlinear Control of Wheeled Mobile Robots [M].Springer，London，2001.

[4]C.A.Canudas de Wit,Theory of Robot Control [M].Springer, London,1996.

[5]黄麟，孙俊.改进QPSO 算法的移动机器人轨迹跟踪控制方法[J].计算机工程与应用，2012，34.

[6]张驰.采用惯性测量单元的移动机器人轨迹跟踪方法研究[J].控制理论与应用，2013，3.

[7]朱群峰，黄磊.移动机器人运动轨迹控制系统[J].信息化纵横，2009，14.

[8]张毅，罗元，郑太雄.移动机器人技术及其应用[M].北京:电子工业出版社，2007.

[9]A. P. Augiar, Performance limitations in reference tracking and path following for nonlinear systems[J].Automatica，2008，44.

[10]P. V.Kokotovic, Singular perturbation methods in control: analysis and design[M]. Academic Press, Orlando，1986.

[11]Yu. G. Martynenko, Motion control of mobile wheeled robots[J].Fundamentalnaya i prikladnaya matematika, vol.11，No.8，2005.