基于双飞轮陀螺效应的两轮自平衡机器人的研制

李 勇，耿建平，林群煦，张 弓，王卫军

（1.桂林电子科技大学，广西 桂林 541000；2.广州中国科学院先进技术研究所，广东 广州 511400；3.深圳先进技术研究院，广东 深圳 518055）

0 引言

轮式移动机器人具有成本低、结构和控制简单、能量利用率高等特点而得到广泛重视[1]。其中两轮（前、后排布的）机器人主体狭长、动作灵活，适合在狭窄路径高速运行；并能适应复杂路况，特别是在地势起伏波动较大的路况下行驶[2]。可望应用于山区、荒野、偏远地区、受灾地区的物质运送，以及军事侦查等领域，因此其研究在世界范围内引起了许多研究者的兴趣。

采用基于飞轮陀螺效应的自平衡技术还有望解决抗撞击能力弱、运行速度较低等问题。本文从理论基础，动力学模型，机械结构，控制系统总体结构等方面介绍了自平衡机器人的研制特点。

1 理论基础

1.1 陀螺效应原理

如图1 所示，飞轮的自转轴为z 轴，相对自转轴的转动惯量为J0的飞轮，以ω0的角速度旋转。令飞轮绕垂直于轴Z 轴的偏转轴X 轴以ω1角速度偏转时。因为陀螺效应，飞轮将产生一个方向沿轴y 轴的力矩M[13]：

图1 陀螺效应Fig.1 The gyro-effect

由此可见力矩M 的方向沿着y 轴正方向。以此为基本理论基础设计了单飞轮自平衡系统：通过控制飞轮的偏转方向，产生合适大小，合适方向的修正力矩，维持系统的平衡。为双飞轮自平衡机器人奠定基础。

1.2 单飞轮自平衡系统

单飞轮自平衡装置结构图如图2（b）所示，飞轮在飞轮框架内由高速电机带动，转速可达10000rpm 以上。偏转电机固定在外框架上，并可驱动飞轮框架连同飞轮发生偏转；偏转角度传感器用于检测实际的偏转角度。外框架的底部与倾斜转轴固连，并能向左或右倾斜；外框架上的姿态传感器用于测试外框架倾斜的角度及角速度。单飞轮自平衡装置的工作原理如下：姿态传感器检测到外框架向左或右倾斜的角度和角速度后，控制偏转电机带动飞轮发生相应的偏转从而产生修正力矩，令外框架回复到竖直状态。

1.3 单飞轮自平衡系统动力学模型

建立固定坐标系O1－X1Y1Z1（图2（b）），原点O1在倾斜转轴的中心轴上，X1轴与倾斜转轴的中心轴重合（图中未显示），Y1轴方向为水平向右，Z1轴方向竖直向上。外框架坐标系O2－X2Y2Z2与外框架固连，原点O2与点O1重合，X2轴与X1轴重合（图中未显示），Y2轴方向平行于外框架底边右，Z1轴垂直于外框架底边且向上。图2（b）显示了外框架相对于固定坐标系向右倾斜的图像。把高速电机、飞轮、飞轮框架、外框架、偏转电机和偏转角度传感器等组成的整体称为主体。图2（a）为主体的力学模型，主体的重量为G，重心与倾斜转轴的距离为h，主体相对于倾斜转轴的转动惯量为J，受到来自飞轮产生的修正力矩（令外框架回复竖直状态的力矩）MR。可以得出以下关于力矩的方程式：

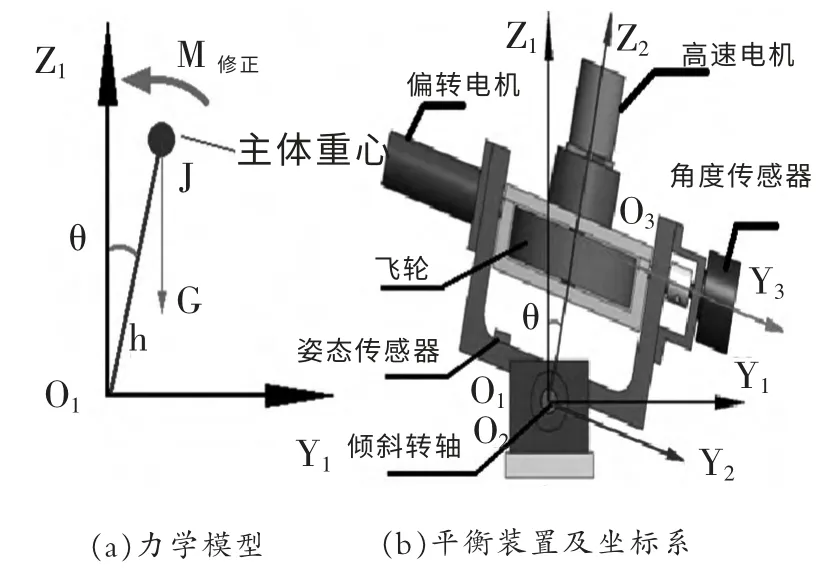
图2 单飞轮自平衡系统力学分析Fig.2 The mechanics analysis of automatic balance based on solo wheel

上式中，μ1表示与角速度θ·相关的摩擦系数。由公式（1）可得：

从式（2）和（3）可知，当偏转电机采用直流电机时，只需要根据外框架的倾斜角度θ 来控制偏转电机的转速ω1，就可以实现单飞轮的自平衡。为了简化模型，此处采用简单的PD 控制策略，即其中K1和K2为待定系数，通过多次实验可以得到。

1.4 单飞轮自平衡系统实验测试

单飞轮自平衡实验平台如图3 所示。通过上位机采集姿态传感器的数据，用Matlab 绘制单飞轮自平衡系统的动态姿态图像。分别进行了静止条件下，运动条件下和撞击条件下的实验。

图3 单飞轮自平衡装置Fig.3 The automatic balance device based on solo wheel

参考图3，平衡装置静止条件下的实验，由于飞轮自转轴在绕垂直Z 轴正方向的轴Y 轴转动时，提供了修正力矩，使外框倾斜角维持在0.5°左右。表现了良好的平衡性能。

参考图3，平衡装置沿X 轴方向上的加减速运动实验。在X 轴方向上有较大加速度（15m/s2）时，外框架倾斜角度达到了10°，在飞轮陀螺效应的作用下，外框架恢复了平衡状态。

参考图3，平衡装置沿Y 轴方向上的撞击试验。将M=1kg 的铁块从高度H=500mm 以钟摆式下落，在最低点以沿Y 轴方向的速度撞击平衡装置外框，撞击后反弹高度h=150mm，取G=10m/s2则平衡系统受到的外部冲量大小，即P=5.48kgm/s2。

在陀螺高速自转条件下（ω＞10000rpm），陀螺进动理论忽略了陀螺的惯性，也即只要有力矩是沿着除飞轮自转轴以外的其他轴向，陀螺自转轴立即以与外力矩作用方向垂直的角速度进动。这样务必给施力者一个反力矩。就是由于陀螺效应的无惯性，实验发现即使发生了强烈碰撞事件，也仅仅导致外框架倾斜角度为8°，碰撞结束后在飞轮陀螺效应的作用下外框架恢复了竖直状态。

通过上述实验，验证了该平衡系统的良好平衡性能，特别是在受到强烈撞击时仍能很快回复平衡状态。依此为基础设计了双飞轮自平衡机器人。

2 双飞轮自平衡机器人

图4 （a）自平衡机器人结构图和（b）修正力矩Fig.4 (a)The structure of self-balancing robot and(b)corrective moment

平衡系统结构示意图如图4（a）所示，前后两飞轮在飞轮框架内由高速电机带动，转速可达10000rpm 以上。偏转电机固定在外框架上，并可以通过传动机构驱动两个陀螺组件绕各自的偏转轴发生偏转；角度传感器用于检测实际的偏转角度。外框架分别与前后轮固定连接，并能向左（Y 正方向）或右（Y 负方向）倾斜。自平衡机器人的工作原理如下：根据车体左或右倾斜的角度，控制偏转电机带动前后飞轮绕偏转轴偏转从而产生修正力矩，保持竖直状态。

系统动力学模型：两个飞轮组件在偏转电机作用下，绕各自偏转轴转动时，效果如图4（b）所示。其中Jz2、Jz3分别表示飞轮相对自转轴的转动惯量。ωz2、ωz3分别表示两飞轮的自转角速度。用于前飞轮和后飞轮通过传动机构连接所以它们角速度大小ωY2=ωY3。

由陀螺效应理论得知，Mx2和Mx3在X1轴方向的分量力矩的和为Mx1，大小为：

Mx1的方向可通过控制偏转电机的转向实现在X1正方向和负方向的变化。进而整个平衡系统可以简化为一个倒立摆模型。

通过修正力矩Mx1抵消重力力矩实现整个系统的竖直方向上的平衡状态。为了简化控制，在不考虑cosα影响的前提下，为了达到两轮机器人自平衡的目的，就需要对飞轮的偏转角速度ωY2进行控制，从而产生适当的修正力矩令其从偏离状态回复到竖直状态。

3 系统总体设计

自平衡机器人系统以STM32F103 单片机控制核心。通过采集外框架的左右倾斜的角度，控制偏转电机一定的角速度偏转。此外通过蓝牙，可以无线遥控机器人的前进、后退，加速、减速、转向等动作。并通过蓝牙无线发送机器人的姿态数据，上位机接收后通过Matlab 绘制平衡系统的随时间变化的姿态动态图。

4 系统硬件结构

电源模块。本系统除了常用的3.3V 电源外，还有维持飞轮高速转动的电源。该电源采用LM2678 构成输出12V（5A）供给飞轮转动。

蓝牙通信模块。采用HC-06，其有四个引脚VCC，GND，TXD 和RXD，输出端为TTL 电平，将外界的蓝牙通信转换为单片机的串口通信（或者将单片机的串口通信转化为外界的蓝牙信号）。

电机驱动模块。采用主流芯片L298N 构成电机驱动模块。本系统采用两路驱动模块分别控制偏转电机和后轮驱动电机。分别实现陀螺组件的偏转和整个机器人的加速，减速，前进，左拐等的动作。

5 系统软件结构

由公式（4）得，控制系统的修正力矩MX1决定于两个飞轮的偏转角速度ωY2和ωY3，而偏转角速度和角加速度由偏转电机的输出驱动力矩M电机决定，而本系统使用的是直流电机，所以电机可通过PWM 控制偏转电机。设控制偏转电机的PWM 占空比为DR。本平衡采用简单的PD 控制策略，当检测到外框架发生倾斜角度为θ，角速度θ·时。令DR= K1θ+K2θ·。其中K1和K2为待定系数。

6 实验

如图5 所示的实物图。在自平衡机器人运动过程中进行各种外干扰实验（急转弯，加减速，撞击），上位机通过无线接收自平衡机器人的外框架姿态数据，通过Matlab 绘制动态图像。

图5 自平衡机器人Fig.5 Self-balancing robot

7 结束语

通过实验可知，基于双飞轮陀螺效应的自平衡机器人科技解决目前国内已有的平衡技术的不足，特别是在有外干扰时（外界撞击）,仍可维持平衡状态。后期通过电子技术和机械设计的结合,双飞轮自平衡技术有望实现急速转弯下的平衡控制，高速下平衡控制以及外界更强烈的撞击下的平衡控制。

[1]刘静，等. 移动机器人技术研究现状与未来[J].机器人，2002，7.

[2]孟祥珺.一种变结构自平衡两轮机器人研究[D].北京邮电大学，2012.

[3]村田顽童最新“超能力”. 电子工程专辑：http://www.eet-china.com/ART_8800548542_480501_NT_c82fc714.HTM，2008/10/17.

[4]Shu-Jen Tsai. Enrique D. Ferreira and ChristiaanJ.J.Paredis.Control of the Gyrover:A Single-Wheel Gyroscopically Stabilized Robot[J].IEE/VRSJ Intelligent Robots and Systems. 1999.

[5]丹尼尔·基勇·金，凯文·布莱特尼，安德鲁·L·曾.陀螺稳定式车辆[P]. 201180024268.3.

[6]Defoot M. Murakami T. Sliding-mode control scheme for an intelligent bicycle[J].IEEE Transactions on Industrial Electronics September，2009，9.

[7]Yamakita M., Utano A. Automatic control of bicycles with a balancer[C]. Proceedings of IEEE International Conference on Advanced Intelligent Mechatronics July 2005，Monterey CA 2005.

[8]郭磊，廖启征，魏世民，等. 独轮车机器人的动力学建模与非线性控制[J].系统仿真学报，2009.

[9]Yavin Y. The derivation of a kinematics model from the dynamic model of the motion of a riderless bicycle[J]. Computers and mathematics with Applications，2006，51.

[10]董文浩. 单轮机器人的控制器设计与侧平衡实验验证[D].哈尔滨工业大学，2012，7.

[11]王攀. 独轮机器人全方位姿态控制研究及实验验证[D].哈尔滨工业大学，2013，6.

[12]Bui T.,Pamichkun M. ,Le C.H. Structure-specified H-loop shaping control for balancing of bicycle robots: A particle swarm optimization approach. Proceedings of the Institution of Mechanical Engineers[J].Part I:Journal of Systems and Control Engineering November 2010，7.

[13]廖耀发，余守宪. 陀螺与陀螺仪进动及章动的一种初等分析[J].湖北工学院学报，2004，10.