火星进入段纵向脱敏局限性分析与三自由度脱敏设计
2015-01-25刘一武
龙 也,刘一武
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
0 引言
以实现0.1 km定点着陆精度为目标的火星精确着陆问题是目前火星探测进入、下降和着陆(Entry,Descent and Landing,EDL)过程制导、导航与控制技术研究的热点[1-2]。而作为EDL过程中气动环境最恶劣、高度跨度最大,参数变化及不确定性最多的阶段[1],火星进入段的末端状态精度对前述目标实现非常关键。为此需深入研究影响进入段制导精度的具体因素及高精度鲁棒制导的实现途径[2]。
研究表明,进入状态偏差是引起进入段末端状态偏差的主要扰动来源之一[3]。目前,在“火星科学实验室”等实际探测任务中得到应用的“解析预测校正进入制导方式”存在一定缺陷,它对进入状态偏差敏感,需严格保证精度,否则初始偏差经进入段误差传播可能引起较大着陆误差[2],而相关鲁棒制导律的研究[4-5]则集中在制导跟踪的鲁棒性上,缺乏针对扰动来源的直接优化。相对而言,基于脱敏最优控制(Desensitized Optimal Control,DOC)的制导方法[6-9]提供了一种新的设计思路,它通过在性能指标中添加特定形式的“系统对状态扰动敏感度”罚项来获得具有相应脱敏特性的标称轨迹,从而实现针对性的制导鲁棒性提升。但目前该类方法通常采用反转逻辑[10-11]控制横程偏差,以倾侧角反转可瞬时完成为假设前提,未考虑实际过程中倾侧角调整能力的限制。
本文在考虑前述问题的基础上针对“进入状态偏差”进行三自由度脱敏轨迹设计研究。全文安排如下:第一节介绍动力学模型、现有纵向脱敏方法及非脱敏方法,第二节分析倾侧角调整性能受束即非理想反转条件下反转逻辑对制导精度的影响,说明纵向脱敏存在的局限性并指出对于脱敏类制导方法采用三自由度设计的必要性,第三节讨论三自由度模型下敏感度传播奇异问题并给出本文设计,第四节进行仿真分析。
1 预备知识
1.1动力学模型与基本约束
考虑自转影响的三自由度火星进入段动力学方程如下:

式中:r为探测器到火星中心距离,v为速度,γ为航迹倾角,s为航程,θ为经度,λ为纬度,ψ为航迹方位角,ωmrs为火星自转角速度,g=μ/r2为探测器所处位置的重力加速度,μ为火星引力常数,σ为倾侧角。L和D分别为气动升力和阻力加速度:

式中:ρ为火星大气密度,采用标准指数型大气模型ρ=ρsexp[-(h/hs)],h=r-rM为所处位置高度,rM为火星半径,ρs为火星表面大气密度,hs为火星大气尺度高度,CL和CD分别为气动升力和阻力系数,Sr为探测器参考面积,m为探测器质量。此外也可采用如下方法计算升阻力加速度:

式中:B为弹道系数,Γ为升阻比系数。
受限于探测器物理参数极限及开伞安全要求,进入段需考虑的基本约束包括最大过载约束、最大动压约束、最大热流率约束等三项过程约束及末端开伞动压约束、速度约束等两项末端约束:
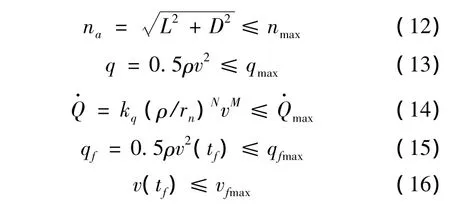
式中:nmax,qmax,,qfmax,vfmax等为前述约束的最大容许值,kq,rn,N,M为热流率计算相关系数。
1.2纵向脱敏方法
纵向脱敏方法采用纵向简化动力学方程,由式(1)~式(4)构成并忽略自转,记为如下形式:
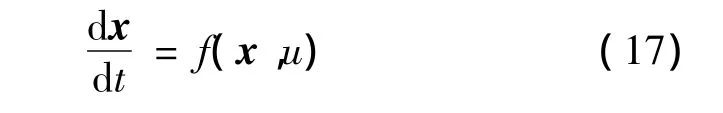
式中:x=[r,v,γ,s]T为系统状态向量,u=cosσ为控制输入,t为时间,f(x,u)为式(1)~式(4)右侧项式。t∈[t0,tf]时,令x(t)=X(t|t0,x0)表示其在初始条件x(t0)=x0下的解,则敏感度矩阵S(t|t0,x0)按下式定义[9]:
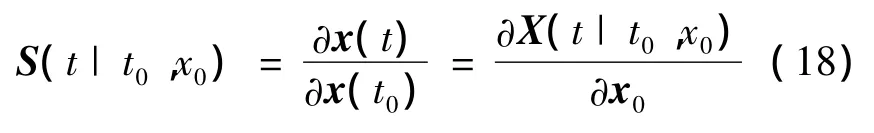
简记为S(t|t0),它满足如下敏感度传播方程[7]:
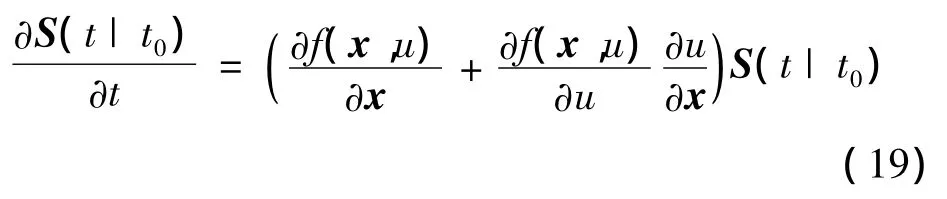
跟踪控制律:
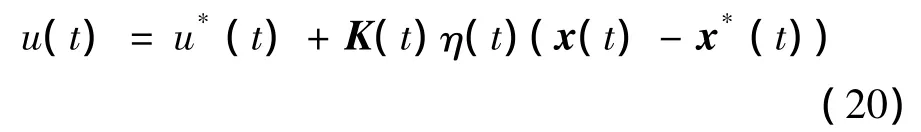
式中:u*(t)和x*(t)分别为t时刻的标称控制量和标称系统状态,K(t)为状态反馈增益阵,η(t)为反馈增益乘子,通常η(t)=1,但考虑控制饱和问题时,部分文献采用如下形式[8]:
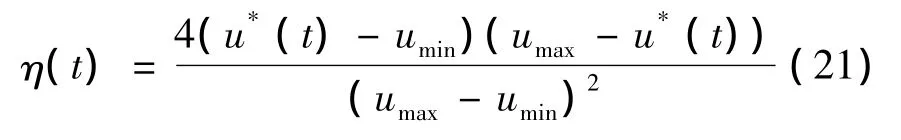
按式(19)积分就能得到轨迹各处对于进入状态偏差的敏感度阵,进而可根据不同设计目标[6,9]计算敏感度罚项,通过优化求解过程得到具有相应脱敏特性的标称轨迹。
1.3非脱敏方法
非脱敏方法用于设计简单的标称轨迹,本文中作为参照衡量其它两种方法性能,轨迹同样通过优化求解过程得到,动力学方程及约束与纵向脱敏方法一致,目标函数为:

式中:J1=-h(tf),Jn2=u2,cn0为惩罚因子。
2 非理想反转对制导精度的影响
反转逻辑的优点在于偏差控制策略的简便性及横纵程设计的解耦特性,因此得到广泛应用[9-13]。但需注意的是,实际过程中探测器的倾侧角调整能力有限,特别是弱机动能力航天器的调整能力更差,这使得真实反转过程不能满足假设前提,从而可能对制导精度造成影响。目前部分文献[12-13]已考虑到该类问题,但通常仅关注如何补偿偏差,较少对其影响制导精度的具体途径进行分析。
事实上,非理想反转引起的直接变化主要包括以下两个方面:一是影响垂直升力分量,使得控制指令偏离标称值,二是导致制导过程出现开环飞行状态。本节从这两点出发讨论其对制导精度的影响,并对纵向脱敏方法在非理想反转条件下的真实受扰程度进行分析(图表均采用第4节设计的相应标称轨迹测试得到)。
2.1升力分量偏离标称值的影响
由倾侧角反转基本定义可知反转过程中探测器垂直升力分量相对标称值偏大,因此航迹倾角会不可避免的有所增加。单次反转过程额外增加的γ总量可按下式估计[14]:
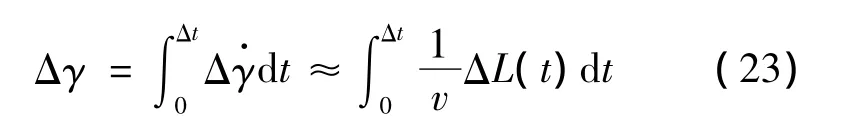
其中单次反转时长Δt可通过假定倾侧角按恒定的最大变化角速度反转进行估算:
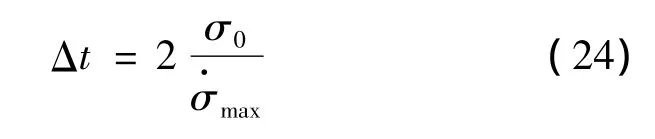
式中:σ0为反转前σ瞬时值。同时垂直升力增量

令LT=CLqSr,将式(25)代入式(23)中整理得:
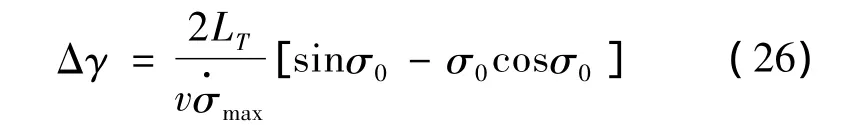
2.2反转过程制导开环的影响
反转过程中制导逻辑默认不进行状态闭环[12],而弱机动能力航天器反转耗时较长,这使得其制导过程会较长时间处于开环状态,导致偏差消除能力下降,间接削弱了制导鲁棒性。
由图2和表1可知,纵向设计的“非脱敏轨迹”应用于真实制导过程时反转次数多达八次,反转过程耗时74.73 s,约占总时长30%左右。由图3可知,制导末端高度及速度标准差会随倾侧角调整能力的下降而趋于增大,即系统对进入状态偏差的敏感度上升,制导鲁棒性下降。

图1 非理想反转条件下开环标称制导末端状态偏差与的关系Fig.1 Relation between open-loop nominal guidance terminal state error and under non-ideal inverse condition
2.3纵向脱敏受扰程度分析
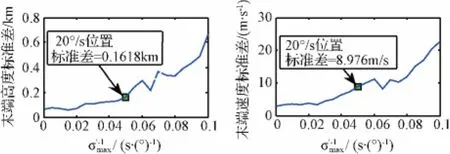
图3 非理想反转条件下闭环制导末端状态标准差与的关系Fig.3 Relation between close-loop guidance terminal state standard deviation andnder non-ideal inverse condition
为充分反映非理想反转对纵向脱敏方法实际制导过程的影响,本节采用“纵向脱敏轨迹”和“非脱敏轨迹”进行对照,观察它们在无进入状态偏差条件下的闭环制导过程以及考虑进入状态偏差问题时的末端状态偏差抑制能力。由图4和图5对比可知,采用纵向脱敏方法时系统在反转完成后易因状态偏差过大而出现持续的控制饱和。由图6和图7对比可知,非理想反转条件下“非脱敏轨迹”末端高度偏差范围为±1 km,速度偏差范围为±50 m/s,而“纵向脱敏轨迹”末端高度偏差范围为 -8~2 km,速度偏差范围为-250~50 m/s。
由此可见,对于纵向脱敏方法,非理想反转容易引起持续的控制饱和并会导致其所设计轨迹在蒙特卡洛仿真测试中不但不能达到预期的制导鲁棒性增强效果,反而出现末端状态偏差散布程度数倍于非脱敏方法的严重失效问题。
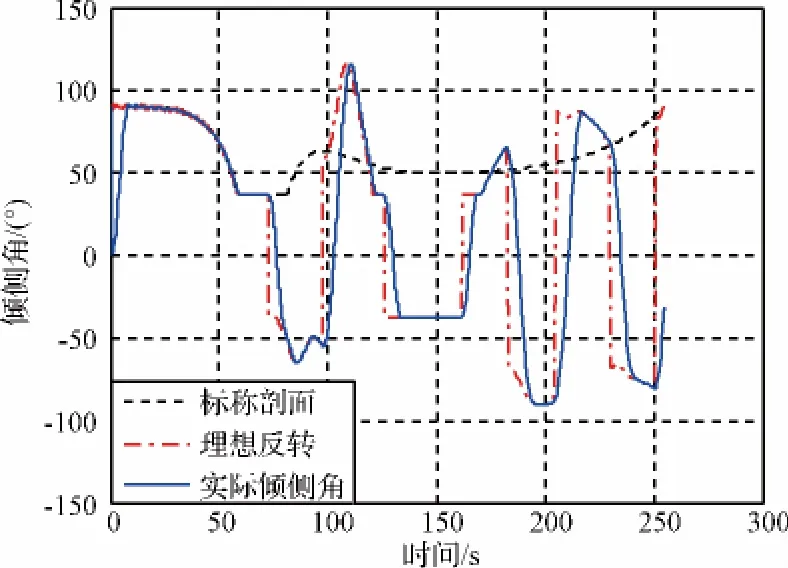
图4 非脱敏轨迹制导过程控制剖面对照Fig.4 Control profile comparison of non-desensitized trajectory guidance process
综上所述,非理想反转对弱机动能力航天器制导精度影响明显,且对纵向脱敏方法影响尤为严重,这说明采用反转逻辑进行横向偏差控制的传统制导策略并不适用于弱机动能力航天器精确制导。因此对“脱敏类制导方法”来说,取消反转逻辑,考虑三自由度模型下的脱敏设计十分必要。

图5 纵向脱敏轨迹制导过程控制剖面对照Fig.5 Control profile comparison of longitudinal desensitized trajectory guidance process

图6 非理想反转条件下非脱敏轨迹末端状态偏差分布Fig.6 Terminal state error distribution of non-desensitized trajectory under non-ideal inverse condition
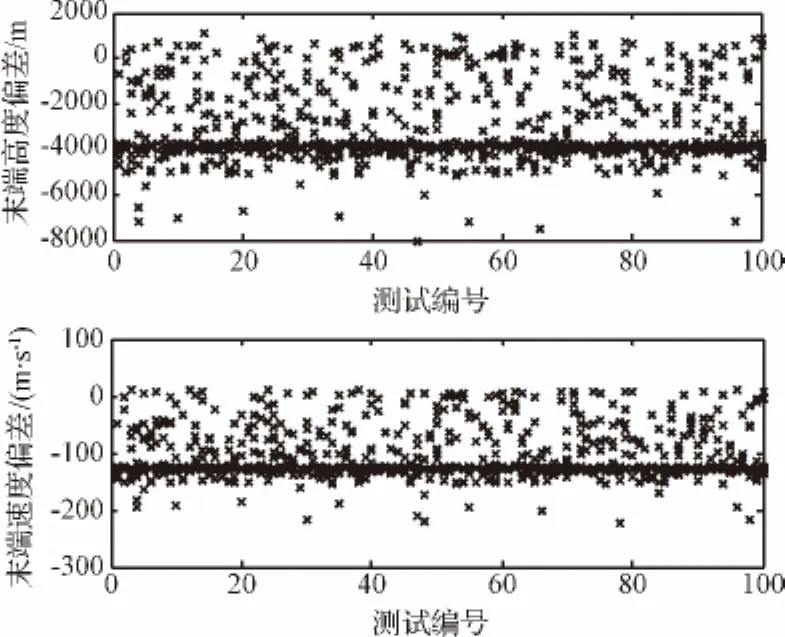
图7 非理想反转条件下纵向脱敏轨迹末端状态偏差分布Fig.7 Terminal state error distribution of longitudinal desensitized trajectory under non-ideal inverse condition
3 三自由度脱敏设计
动力学方程包括式(1)~式(7)并考虑倾侧角调整动态:

式中:σv为倾侧角角速度,uc为倾侧角角加速度。优化求解过程以uc为系统输入。
3.1控制及状态约束
基础约束包括式(12)~式(16),并附加倾侧角范围约束、角速度及角加速度约束:
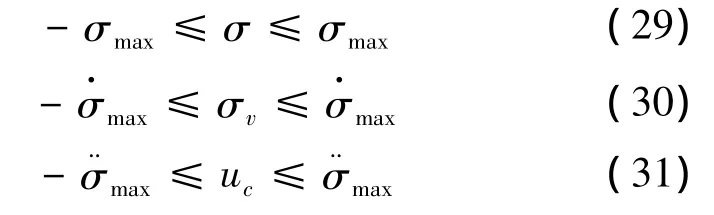
附加末端状态约束:
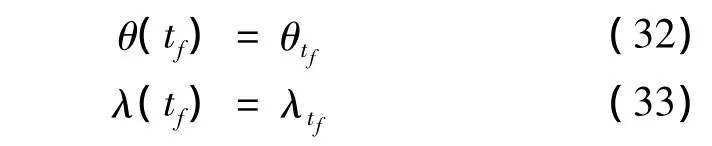
末端航程stf为自由状态,经纬度与预期值θtf,λtf一致时标称轨迹结束。
3.2敏感度传播方程
首先,类似于纵向脱敏方法,考虑x为完整的状态量[r,v,γ,s,θ,λ,ψ]T,f(x,u)为式(1)~ 式(7)右项。此时,敏感度传播方程中∂f/∂u项为:
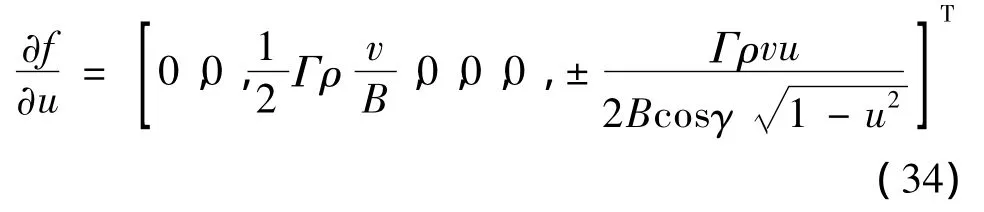
显然u=1时∂f/∂u最后一项变为无穷,出现“奇异问题”,这会导致传播方程无法继续推演,因此前述x与f(x,u)的选取并不合理。
应注意到,在仅考虑纵向剖面的现有脱敏方法中x=[r,v,γ,s]T包括了对末端开伞安全最为重要的高度、速度项,而航程s相当于将耦合的横纵程脱敏问题转化为单一量表示。因此,敏感度传播方程仍采用式(19),跟踪控制律中η(t)=1-(u*(t))2。
3.3目标函数
目标函数的选取包括末端开伞高度和轨迹脱敏两项。一方面,开伞高度是保证探测器安全着陆的重要因素,且开伞高度越高意味着探测任务点可选范围更大[1]。另一方面,S(tf|t0)包含末端状态对进入状态偏差的敏感度信息。因此目标函数J设为:

式中:J1=-h(tf)为开伞高度罚项,c0≥0为敏感度惩罚因子,J2为进入状态偏差敏感度项:
式中:ci≥0,i=1,2,3,4为权重因子,表示对各状态脱敏特性的注重程度。
4 仿真分析
本节首先给出仿真参数,其次分别采用“非脱敏方法”,“纵向脱敏方法”与“三自由度脱敏方法”设计标称轨迹,最后通过蒙特卡洛仿真校验三自由度脱敏的改进效果。其中部分轨迹设计及仿真结果已在前文引用,不再重复给出。
4.1仿真参数
反转逻辑采用的航向误差走廊参数如下[11]:

式中:stgo为待飞航程,航向误差Δaz超出最大允许航向误差Δazm时倾侧角进行反转。其它设计及仿真参数见表2~表5。

表2 相关物理参数Table 2 Related physical parameters
此外 σt0=0,=0,K=-[0.01,0.005,50,0.001]。
对于前两种设计方法,表4中前四项约束保留,且stf=735 km,smax=stf并有umin=-0.8,umax=0.8。
4.2轨迹设计结果
轨迹的优化求解均采用高斯伪谱法[15]实现。图8~图9为三自由度脱敏轨迹设计结果。

表3 控制及过程约束参数[1]Table 3 Control and process constraint parameters[1]
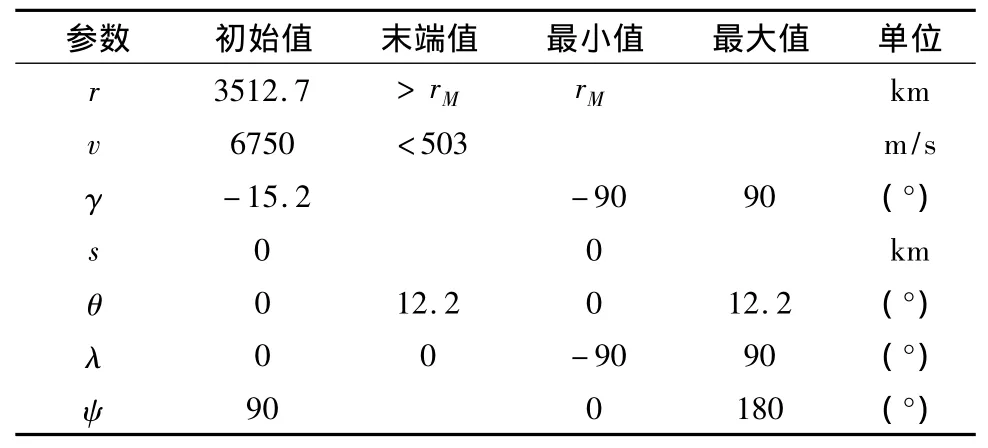
表4 边界条件及约束参数Table 4 Boundary conditions and constraint parameters

表5 蒙特卡洛仿真参数Table 5 Monte-Carlo simulation parameters

图8 c0=0.02、h(tf)=10210 m时三自由度脱敏轨迹标称倾侧角剖面Fig.8 Nominal bank angle profile of three degree of freedom desensitized trajectory corresponding to c0=0.02 and h(tf)=10210 m
图9中倾侧角加速度与速率轨迹表明本文方法在设计时已保证所设计轨迹在探测器倾侧角调整能力范围之内。
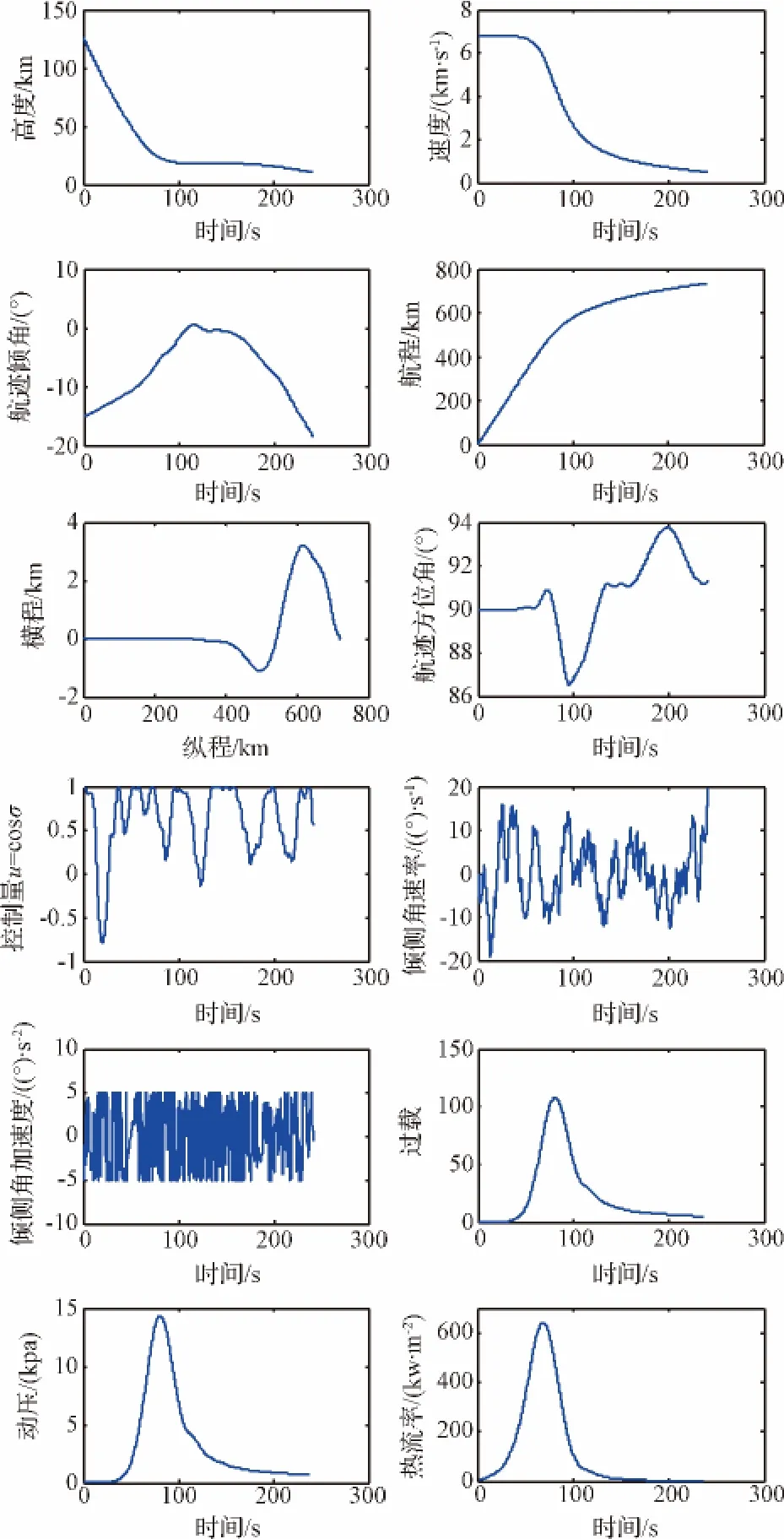
图9 三自由度脱敏轨迹完整信息Fig.9 Complete information of three degree of freedom desensitized trajectory
4.3蒙特卡洛仿真校验
图10为“纵向脱敏轨迹”在纵向剖面内校验时的蒙特卡洛仿真结果,图11为“三自由度脱敏轨迹”在三自由度模型下校验时的蒙特卡洛仿真结果。
图10表明“纵向脱敏轨迹”的末端高度偏差为±50 m,速度偏差为±15 m/s。图11表明“三自由度脱敏轨迹”的末端高度偏差为±10 m,速度偏差为 ±1 m/s,航程偏差为 ±0.2 km,纵向偏差为 ±0.5 km,横向偏差为±4 km。由此可知,本文设计相比现有纵向脱敏方法可更大程度降低系统对进入状态偏差的敏感程度,具有显著增强的鲁棒性能。
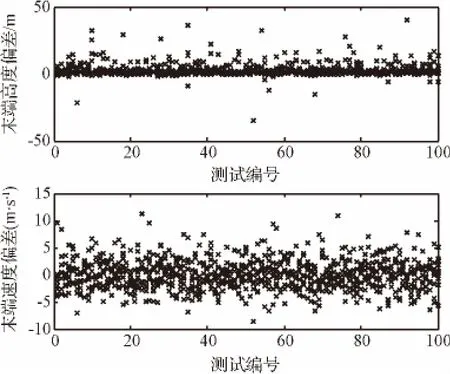
图10 在纵向剖面内校验时纵向脱敏轨迹的蒙特卡洛测试结果Fig.10 Monte-Carlo test results of longitudinal desensitized trajectory when tested in longitudinal profile

图11 三自由度脱敏轨迹的蒙特卡洛测试结果Fig.11 Monte-Carlo test results of three degree of freedom desensitized trajectory
5 结束语
现有纵向脱敏方法通常采用反转逻辑控制横程偏差,但本文研究表明非理想反转会引起末端状态偏差、使系统对进入状态偏差敏感度上升,并且导致弱机动能力航天器采用纵向脱敏方法制导时出现末端状态偏差散布程度数倍于非脱敏方法的失效情况。因此,对于火星进入段制导,本文放弃采用反转逻辑,针对进入状态偏差问题提出了三自由度脱敏设计。仿真结果表明,该方法有效解决非理想反转条件下纵向脱敏方法的严重失效问题,且末端状态偏差抑制能力更强。
目前本文仅考虑了进入状态偏差问题,针对“气动参数不确定”、“过程气动力扰动”的脱敏设计及同时考虑三类扰动形式的完整脱敏方案有待进一步研究。
[1]Braun R D,Manning R M.Mars exploration entry,descent and landing challenges[J].Journal of Spacecraft and Rockets,2007,44(2):310-323.
[2] 崔平远,胡海静,朱圣英.火星精确着陆制导问题分析与展望[J].宇航学报,2014,35(3):245-253.[Cui Ping-yuan,Hu Hai-jing,Zhu Sheng-ying.Analysis and prospect of guidance aspects for Mars precision landing[J].Journal of Astronautics,2014,35(3):245-253.]
[3] 李爽,彭玉明,陆宇平.火星EDL导航、制导与控制技术综述与展望[J].宇航学报,2010,31(3):621-627.[Li shuang,Peng Yu-ming,Lu Yu-ping.Review and prospect of Mars EDL navigation guidance and control technologies[J].Journal of Astronautics,2010,31(3):621-627.]
[4]Mooij E,Mease K D,Benito J.Robust re-entry guidance and control system design and analysis[C].AIAA Guidance,Navigation,and Control Conference and Exhibit,Hilton Head,USA,August,2007.
[5]Lu W M,Bayard D S.Guidance and control for Mars atmospheric entry:adaptivity and robustness[R].AIAA Paper,1999.
[6]Shen H J,Hans S,Richard W P.Desensitizing the pin-point landing trajectory on Mars[C].AIAA/AAS Astrodynamics Specialist Conference and Exhibit,Honolulu,Hawaii,August 18-21,2008.
[7]Seywald H,Kumar R R.Desensitized optimal trajectories[J].Advances in the Astronautical Sciences,1996,93(1):103-115.
[8]Seywald H.Desensitized optimal trajectories with control constraints[J].Advances in the Astronautical Sciences,2003,114:737-743.
[9]Li S,Peng Y M.Mars entry trajectory optimization using DOC and DCNLP[J].Advances in Space Research,2011,47(3):440-452.
[10]Harpold JC,Graves Jr CA.Shuttle entry guidance[J].Journal of the Astronautical Sciences,1979,27(3):239-268.
[11]Tu K Y,Munir M S,Mease K D,et al.Drag-based predictive tracking guidance for Mars precision landing[J].Journal of Guidance,Control,and Dynamics,2000,23(4):620-628.
[12]Carman G,Ives D,Geller D.Apollo-derived Mars precision lander guidance[C].AIAA Atmospheric Flight Mechanics Conference and Exhibit,Boston,MA,August 10-12,1998.
[13]Brunner C W.Skip entry trajectory planning and guidance[D].Iowa:Iowa State University,2008.
[14]Mooij E,Space D.Model reference adaptive guidance for reentry trajectory tracking[C].AIAA Guidance,Navigation,and Control Conference and Exhibit,Rhode Island,USA,August 16-19,2004.
[15]Garg D,Michael P,Hager W,et al.A unified framework for the numerical solution of optimal control problems using pseudospectral methods[J].Automatica,2010,46(11):1843-1851.
