关于高等数学教学中部分知识点的探讨①
2015-01-24陈茜
陈 茜
(中南林业科技大学理学院,湖南长沙10004)
教学授课是一个非常灵活的过程。教师在讲授课本知识的基础上,能够根据教学目标、教学对象、课堂气氛等的需求,及时引入、总结一些教学知识点,会使得教学课堂更丰富,教学对象更受益。为此,我们讨论了高等数学教学中的几个知识点。
1 函数极限教学的调整
极限概念的教学是从数列极限开始的[1]。数列是特殊的函数,在于它的变量只能取正整数,所以数列的极限只讨论n 趋于正无穷时数列收敛的情况。但对于广义上的函数来说,除了x →+ ∞,还有x→- ∞,x →∞,x →a,x →a-,x →a+这5 种方式。那么在学习数列极限的基础上,再引入函数极限时,可首先引入x →+∞时函数的极限。原因在于:两者的自变量都在趋于正无穷,只要将数列自变量取离散正整数的状态推广为连续状态下的正实数,就过渡到了函数的极限。
但在同济版高等数学教材[2]中引入函数极限是从x →a 开始的,随后才是x →∞。这样就将数列和函数在无穷下的极限联系断开,不利于极限概念的深入理解和巩固。
2 等价无穷小替换在幂指函数极限中的应用
对幂指函数求极限,除了教材中涉及到的对数法、恒等变形法来求解外,有很多同学还会有这样的疑问:能否运用等价无穷小替换原理求解,尤其是针对00的未定式。
实际上,如果f(x)和g(x)在x0的某一去心邻域内为连续函数,当x →x0时,若f(x)→0,g(x)→0 且,则
其实对于1∞和∞0这2 种未定式,间接利用上面的结论同样可以得到有效的结论。如:
3 有理函数积分的常见类型
有理函数分为假分式和真分式2 种情况。假分式一般通过多项式的除法可化为整式和真分式。所以有理函数的积分最实质的就是真分式的积分。如果真分式中的分母可以分解因式,真分式必可裂为部分分式之和。最后,真分式的部分分式中只出现和为二次质因式)等两类函数。
在同济第6 版高等数学有理函数的积分教学中[2],认为P1(x)为小于k次的多项式,P2(x)为小于2l次的多项式。我们认为这样的叙述有失严谨性,因为P1(x)到底应是k -1次的,还是k -2次的,还是……,在解题中学生无法清晰把握;对于P2(x)也是同样的情况。实际上将部分分式通分,与原真分式相等下比较分子中x 的幂会得到:P1(x)应是(k-1)次的多项式;P2(x)应是(2l-1)次的多项式。对部分分式中常见的类型:
以上为有理函数积分中常见的三类形式。在具体的题解中这几种形式常常交错出现,使得积分看似繁琐,但掌握其规律并多加练习后就会得心应手。
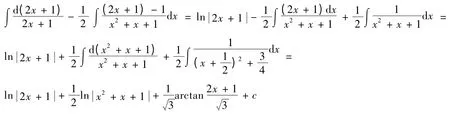
4 微分方程和重积分对称性题目的引入
像这样隐藏初始条件于表达式中,同时还先需求导再明了为微分方程的题目,比较少见。如果能在实际的课堂教学中提出这样的题目给学生思考、求解再总结,这对于学生知识的联系性、思维的发散性和基础功的巩固都非常有利。同样,在现有的教材中对于二重积分知识点的教授没有涉及对称性,但在有些题目中如果利用二重积分的对称性,势必会做到事半功倍。
由二重积分的对称性,第二项积分为零(D 关于y 轴对称,f(x,y)= xy 为x 的奇函数),使得求两个积分减化为求一个积分,简化了计算过程,提高了做题效率。因此,在课堂教学时如果能适当添加这个知识点,并给出几个具体的题目练一练,不但能丰富同学的积分知识,又可为考研这样的大型考试添砖加瓦。
[1]刘玉琏,付沛仁.数学分析讲义[M].北京:高等教育出版社,1995.
[2]同济大学数学系.高等数学[M].6 版.北京:高等教育出版社,2008.
[3]陈茜,舒慧颖.浅析幂指函数的极限问题[J].衡水学院学报,2011(4):8-9.
[4]郝海龙.考研数学复习大全(历年统考真题分类训练)[M].北京:北京航空航天大学出版社,2014.
