变长CD-CAT中的曝光控制与终止规则*

郭 磊 郑蝉金 边玉芳

1 引言

近些年来, 国内外对认知诊断计算机化自适应测验(Cognitive Diagnostic Computerized Adaptive Testing, CD-CAT)的研究越来越多。CD-CAT结合了认知诊断理论和 CAT的双重优势, 比起传统的测验形式, 它可以更精确、更迅速、更灵活地测量出被试的潜在知识结构, 也称为知识状态(Knowledge State, KS), 从而获得被试在知识点上的掌握情况,为教育教学工作提供有针对性的指导, 促进学生的个性化发展。

CD-CAT和传统CAT的组成部分是相似的, 主要包括五部分：(1)参数已知的题库; (2)初始项目选择方法; (3)知识状态或能力值的估计; (4)选题策略;(5)终止规则(陈平, 2011)。由于CD-CAT发展较晚,截止目前, CD-CAT的研究主要集中在选题策略(Cheng, 2009, 2010; Wang, 2013; Wang, Chang, &Douglas, 2012; Xu, Chang, & Douglas, 2003; 毛秀珍, 辛涛, 2011)、项目曝光控制(Wang, Chang, &Huebner, 2011; 陈平, 2011; 毛秀珍, 辛涛, 2013)和属性在线标定(Chen, Xin, Wang, & Chang, 2012; 陈平, 辛涛, 2011; 汪文义, 丁树良, 游晓锋, 2011)方面, 对终止规则的研究相对较少。在查阅国内外关于CD-CAT终止规则的文献后发现, 仅有Hsu, Wang和Chen (2013)专门对变长CD-CAT的终止规则进行过模拟研究, 而大部分的研究还是围绕选题策略、曝光控制和属性在线标定这三方面展开的。但关于这三方面的研究均是以定长(fixed-length) CAT的形式作为终止规则, 即固定每次测验的长度, 当被试完成测验后, 根据被试的作答反应估计知识状态。定长CAT由于固定了测验长度, 施测较为方便,但对不同的被试会有不同的测量精度。一个更加合理的做法是, 应该使得 CAT形式的测验对每个被试的测量精度相同, 这也正是自适应测验的优势所在(Weiss & Kingsbury, 1984)。与定长CAT相对应的终止规则为变长(variable-length)CAT, 变长 CAT能够达到每个被试具有相同测量精度的目标, 具有更高的估计精度(Babcock & Weiss, 2009)。Kingsbury和 Houser (1993)的研究表明, 不管是在多级评分CAT还是0-1评分CAT中, 变长CAT在测验效率、能力估计的收敛和能力估计精度等方面均优于定长 CAT。相对于定长 CAT, 变长 CAT更能体现出自适应的特点和优势, 因此, 开展这方面的研究非常有意义。在传统CAT中, 一些学者对变长CAT的终止规则进行了相应的研究(Choi, Grady, & Dodd,2010; Dodd, 1990; Dodd, Koch, & De Ayala, 1993;Dodd, De Ayala, & Koch, 1995), 总体来讲, 可以归纳成两类：(1)不断施测项目直到测量标准误落在可接受范围内, 或测验信息量达到某个预先设定的指标; (2)最小信息量终止规则, 即剩余题库中所有项目的项目信息量都低于某个预设水平(陈平, 2011)。在CD-CAT中, Hsu等(2013)在Tatsuoka (2002)提出的基于后验概率序列方法的基础上稍做改进, 提出了变长CD-CAT的终止规则(本文将其称为HSU法,详见第2部分)。其研究结果表明, 当固定知识状态后验分布的最大后验概率预设水平时, 被试的模式判准率会随着第二大后验概率预设水平的降低而增大; 当固定知识状态后验分布的第二大后验概率预设水平时, 被试的模式判准率会随着最大后验概率预设水平的升高而增大。这是对变长CD-CAT研究的一大推动。

与传统CAT一样, 在CD-CAT的实际应用中,不容忽视的一个重要问题是项目曝光问题。Wang等(2011)在研究中指出, 当前 CD-CAT着重于测量精度的实现, 未考虑到项目曝光问题, 导致题库使用极其不均匀, 优质题目曝光十分严重。尽管CD-CAT不是高风险测验, 但当认知诊断结果与某些教学评价指标挂钩时, CD-CAT就会变得具有高风险, 测验安全将变得十分重要(毛秀珍, 辛涛,2013; 唐小娟, 丁树良, 俞宗火, 2012)。而且CD-CAT的题库建设比传统 CAT建设更加复杂耗时, 除了像传统 CAT要考虑题目质量等因素之外, 还要对每道题目测查的属性(即Q矩阵)进行详细准确的界定, 如果优质题目过度曝光, 将会导致资金和时间的严重浪费。因此, 在CD-CAT中对项目曝光率进行控制具有重要意义。

正如前文所述, 仅有 Hsu等(2013)对变长 CDCAT的终止规则进行过模拟研究, 更多的文献仅在讨论部分提出了研究变长 CD-CAT的重要性和必要性, 缺乏对具体方法的研究, 更缺乏在变长 CD-CAT下控制项目过度曝光的研究。例如, Cheng (2008)提出可以求取邻近两次后验分布的KL距离, 当该距离小于预设水平时即可终止测验的方法。本文首先借鉴前文总结的传统变长 CAT的终止规则, 提出了两种变长CD-CAT的终止规则, 分别称作属性标准误法(standard error of attribute, SEA)和二等分法(halving algorithm, HA)。然后从估计的相对稳定性角度提出了邻近后验概率之差法(difference of the adjacent posterior probability method, DAPP)。最后, 将相对稳定性的思想与Tatsuoka (2002)提出的经验性准则相结合, 提出了混合法(hybrid method,HM) (参见本文第 2部分)。接下来以 DINA模型(Junker & Sijtsma, 2001)为例, 在未控制曝光和采用不同的曝光控制条件(参见本文第 3部分)下, 将四种新方法与HSU法以及Cheng提出的KL法进行比较, 意在全面考察不同的变长CD-CAT终止规则在不同实验情景下的实际表现。

2 变长CD-CAT终止规则

本文所涉及的6种变长终止规则可以归纳为三大类：第一类是基于绝对标准的终止规则, 包括HSU法, SEA法和HA法; 第二类是基于相对标准的终止规则, 包括DAPP法和KL法; 第三类是结合两种标准的终止规则, 即混合法。其中, HA法属于项目水平(item-level)的终止规则, 即终止规则是从题目角度出发判断的; 其余5种方法属于被试水平(examinee-level)的终止规则, 即终止规则是从被试自身的角度判断的。下面分别对本文涉及的6种方法进行介绍。

2.1 HSU法

Tatsuoka (2002)给出了变长CD-CAT的经验性准则, 即被试属于某种知识状态的最大后验概率超过 0.8时, 测验终止。Hsu等(2013)基于 Tatsuoka的思想, 进一步提出了双重标准的变长CD-CAT终止规则, 即当被试属于某个知识状态的最大后验概率 P不低于某个预设水平(例如, 0.7), 并且第二大后验概率P不高于某个预设水平(例如, 0.1)时,测验终止。

2.2 属性标准误法(standard error of attribute method, SEA)

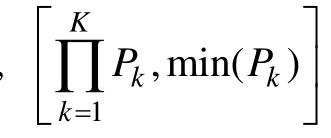
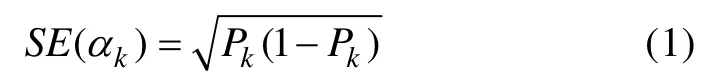
其中, S E(a) 为属性k的标准误, k = 1 ,2,K ,K。P为掌握属性k的边际后验概率。SEA法的测验终止规则为：被试每做完一道题目, 便计算每个属性的标准误, 直到所有属性的标准误均小于预设水平时(例如, 0.2), 测验终止。

2.3 二等分法(halving algorithm, HA)

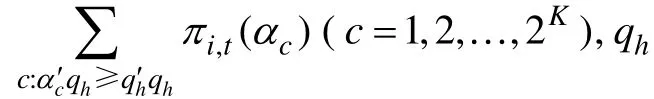
2.4 邻近后验概率之差法(difference of the adjacent posterior probability method, DAPP)

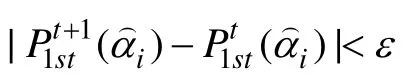
2.5 KL距离法

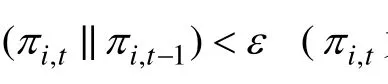
2.6 混合法(hybrid method, HM)

3 选用的认知诊断模型、选题策略及曝光控制方法

3.1 认知诊断模型—DINA模型

DINA模型属于非补偿模型, 每道题目只有两个参数：s参数和g参数。记二分变量 X为被试i对项目 j的作答反应( X= 1 表示答对, X=0表示答错), 知识状态为a的被试在第j题上正确作答的概率可以表示为：

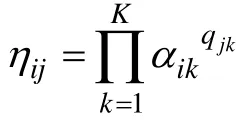
3.2 选题策略

根据已有研究结果表明, 后验加权的 KL信息量法(PWKL), 综合后验加权和距离加权的混合KL信息量法(HKL)以及香农熵法(SHE)均具有较高的属性判准率和模式判准率(Cheng, 2009; 陈平,2011)。本文按照Hsu等(2013)的做法, 选取PWKL作为变长CD-CAT的选题策略。PWKL指标的计算公式如下：

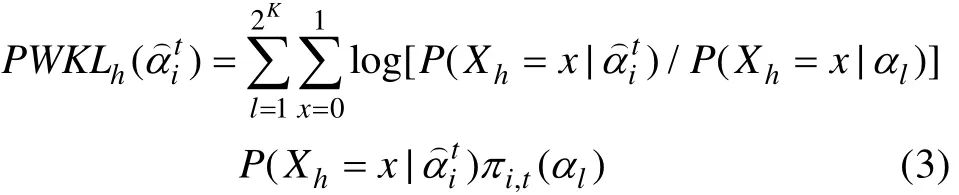
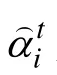
it l知识状态a的后验概率。运用PWKL时, 从剩余题库中选择具有最大 PWKL信息量的题目作为下一题施测。

3.3 曝光控制方法

Wang等(2011)将应用于传统CAT中的曝光控制方法进行了修正, 并加入了重要参数(importance parameter), 提出了两种适用于定长 CD-CAT的曝光控制方法：限制进度法(Restrictive Progressive method, RP)和限制阈值法(Restrictive Threshold method, RT)。RP法(或RT法)通过运用“进度因子”1/xL- (x为已施测的题目数量, L为测验长度)来分配随机成分(或阈值大小)和信息量在选题指标中的权重, 从而达到控制项目过度曝光的目的。进度因子1/xL-的含义为：在测验初始阶段, 进度因子接近于 1, 选题指标的大小基本上由随机成分的大小决定, 信息量的作用很小; 随着测验的进行, 进度因子逐渐减小, 选题指标主要由信息量的大小决定, 随机成分的作用变得很小。显然, 进度因子的计算依赖于测验的固定长度 L, 因此, 这两种方法只适用于定长CD-CAT情景。本文将 RP法和 RT法进行修正(详见 3.3.2和 3.3.3部分), 分别称作修正的限制进度法(Modified Restrictive Progressive,MRP)和修正的限制阈值法(Modified Restrictive Threshold, MRT), 使之适用于变长CD-CAT情景。同时考虑第三种项目曝光控制方法：简单控制法(simple), 并采用以上三种方法分别对 CD-CAT测验进行曝光控制。接下来, 分别对这三种项目曝光控制方法进行介绍。

3.3.1 simple法

simple法是在 PWKL选题策略指标前乘以一个曝光控制因子f (陈平, 2011), 计算公式如下：

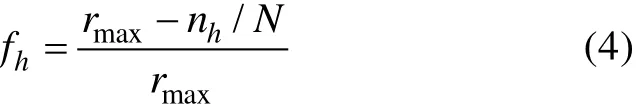
其中,r 为允许的最大项目曝光率,n为第h个项目当前的被调用次数, N为参加测验的总人数。

3.3.2 MRP法

在定长CD-CAT中, RP法中的进度因子由已施测的题目数量和测验长度之间的关系描述。类似地,MRP法利用当前最大后验概率和预设最大后验概率之间的关系来重新定义“进度因子”。同时, 根据Wang等(2011)的预实验结果, 只在RP方法中加入随机成分并不足以保证能够有效地控制所有过度曝光的项目。因此, 需要引入曝光控制因子f来将所有项目的曝光率控制在预设水平以下。MRP法对进度因子进行了重新刻画, 同样需要引入f对过度曝光项目进行控制。于是, MRP法将在剩余题库中选择具有最大 M RP_ P WKL值的项目进行施测：

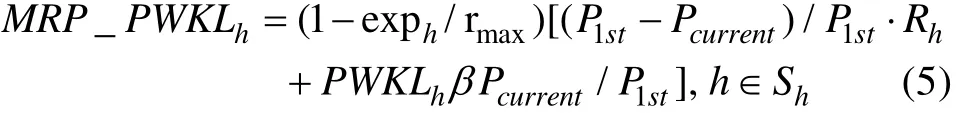
其中, P为最大后验概率的预设水平, P为当前属于某个知识状态的最大后验概率。S为剩余题库, exp为项目 h当前的曝光率。记 H为S中项目信息量最大值, 则随机成分 R～ U ( 0,H)。b为平衡测量精度和项目曝光率的指标。

3.3.3 MRT法

该方法根据选题策略(本文使用的是PWKL选题策略)从剩余题库中选出符合要求的项目构成候选项目集, 然后再根据一定原则从候选项目集中选出下一题(本文采用的是随机方法)。符合要求的候选项目落在区间[max(P WKL ) - d,max(P WKL)]内。其中, 区 间 长 度 d = [ max(P WKL ) - m in(P WKL)]×(1-P/ P)。值得注意的是, 当使用 MRT法时,作者发现有些曝光率大于 r的项目仍会被选中,这是因为 P的增长并非线性增长, 存在“折回”现象, 即下一阶段的 P会小于上一阶段的P。因此, 在使用MRT法时, 需要将越界的项目从题库中剔除, 保证参加测验的被试在今后测验中不再使用该题。

4 方法

本文采用Matlab (R2011b)自编所有程序, 进行模拟实验。

4.1 题库及被试生成

本研究题库及被试的知识状态采用陈平等(2011)的方法生成。陈平等(2011)在假设属性之间相互独立前提下, 给出了三种类型的基本Q矩阵, 分别称作Q、Q和Q矩阵。然后对它们进行简单操作后, 生成考察6个属性, 共360道题目的题库。题库中的猜测参数 g和失误参数 s从均匀分布U(0.05,0.25)中抽取。生成2000名被试并且假设每个被试掌握每个属性的概率是0.5。

4.2 模拟作答及KS估计方法

运用DINA模型计算被试i在题目j上的正确作答概率P, 然后从 (0,1)U 分布中产生一个随机数m。如果P大于等于m, 则被试i在题目j上的作答反应记为 1, 否则为 0。在被试进入 CD-CAT时, 首先随机生成被试的知识状态, 在被试每作答完一道题目后, 运用贝叶斯最大后验概率方法(Maximum A Posterior, MAP)估计被试的知识状态。

4.3 终止标准设置

(1)P包含两个水平：0.8和0.9; P包含两个水平：0.002和0.003;

(2)由于尚无e在不同终止规则下的研究, 因此,本文首先对e在不同终止规则下得到的测验使用情况和模式判准率进行了预研究(由于篇幅所限,未将预研究结果列出, 并不妨碍对本文的理解),以此确定出了不同终止规则下e合理的取值条件,具体为：在使用HM法、DAPP法和KL法时, e包含 4个水平：0.05、0.01、0.005和 0.001; 在使用SEA 法时, e包含 5个水平：0.3、0.25、0.2、0.1和0.05; 在使用HA法时, e包含5个水平：0.1、0.05、0.01、0.005和0.001;

(3)当加入项目曝光控制因子时, 固定r值为行业标准0.2, 2b=。同时, 为了不让变长CD-CAT的题目数量过长, 与实际情况更加贴近, 本文设置测验长度的上限为30题。

综上所述, 本研究共涉及 4种曝光控制条件(无控制、simple法、MRP法和MRT法)和6种终止规则。并且, 根据预研究确定出了每种终止规则下的终止标准, 分别为：HSU法4个水平、SEA法5个水平、HA法5个水平、DAPP法4个水平、KL法4个水平和HM法4个水平。为了减小随机误差, 每种实验条件均实验 30次。最终共需进行4´ ( 4 + 5 + 5 + 4 + 4 + 4 )´ 3 0 = 3 120次实验。

4.4 评价指标

被试知识状态估计精确性的指标为模式判准率(Pattern Correct Classification Rate, PCCR), 计算公式如下：

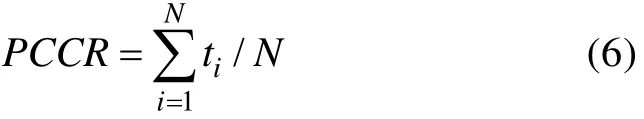
PCCR考察被试属性掌握模式(a =(a,a,K ,a))的返真性。假设测验共考察了K个属性, 有N个被试参加了测验, 发生失误前(即理想状态下)被试 i的属性掌握向量记为 X, 但把该被试归类为Z, 如果有 X=Z, 记 t= 1 ; 否则记 t= 0 。

同时, 还记录了测验长度(平均数, 标准差, 测验最长值和测验最短值)、未使用的题目数量等指标来衡量不同终止规则表现的差异。

5 结果与讨论

5.1 未加入曝光控制的实验结果与讨论

表1是在未加入曝光控制方法下, 6种终止规则的CD-CAT测验使用情况和模式判准率结果。从表1可以看出, 6种变长终止规则均有很好的表现,彼此差异不明显。总体来看, 随着P的增大和e的减小, 测验平均用题量逐渐上升, 题库中未使用的题目数量逐渐减小, PCCR值逐渐上升。这是因为终止规则越严格, 被试需要作答更多的题目才能达到终止标准。作答的题目数量越多, 被试能够提供的信息量也就越多, 于是被试属于某一知识状态的可能性就越大。

具体来看, 在HSU法中, 只控制P时的PCCR值要小于同时控制P和P的 PCCR值(0.8394<0.9968, 0.9219<0.9980), 未使用题目数量为前者多于后者, 但在平均用题量上, 前者要少于后者, 这跟 Hsu等(2013)的研究结果一致。在 HM 法中,e=0.001时的结果与 HSU法中同时控制条件下的实验结果(即表1中第8行与第2行, 第12行与第4行)相似; 当e=0.05时, 平均用题量分别增加了2.8 题(12.0–9.2)和 1.5题(12.9–11.4), 而 PCCR 值分别提升了 9.63% (0.9357–0.8394)和 3.67% (0.9586–0.9219)。在SEA法中, 当e=0.3时, PCCR值只有0.7963, 平均用题量为8.6题; 当e=0.25时, PCCR接近但仍然低于0.9, 但当e=0.2时, PCCR值上升至0.9672, 与HSU法的第三行结果相比, 平均用题量只多了1.3题(12.7–11.4), 而PCCR值上升了4.53%;当e=0.05时, PCCR高达0.9927, 与HSU法的第四行结果相似。在DAPP法中, 当e=0.05时, PCCR值非常低, 只有 0.3387, 平均用题量只作答了 5.6题; 但当e=0.01时, PCCR值立刻增长到 0.9885,平均用题量也上升到 15.9题, 当e继续下降至0.001时, PCCR值高达0.9989, 并且题库中未使用的题库数量也由240题下降至102题。KL法以及HA法和DAPP (SEA)法结果类似, 故不再赘述。

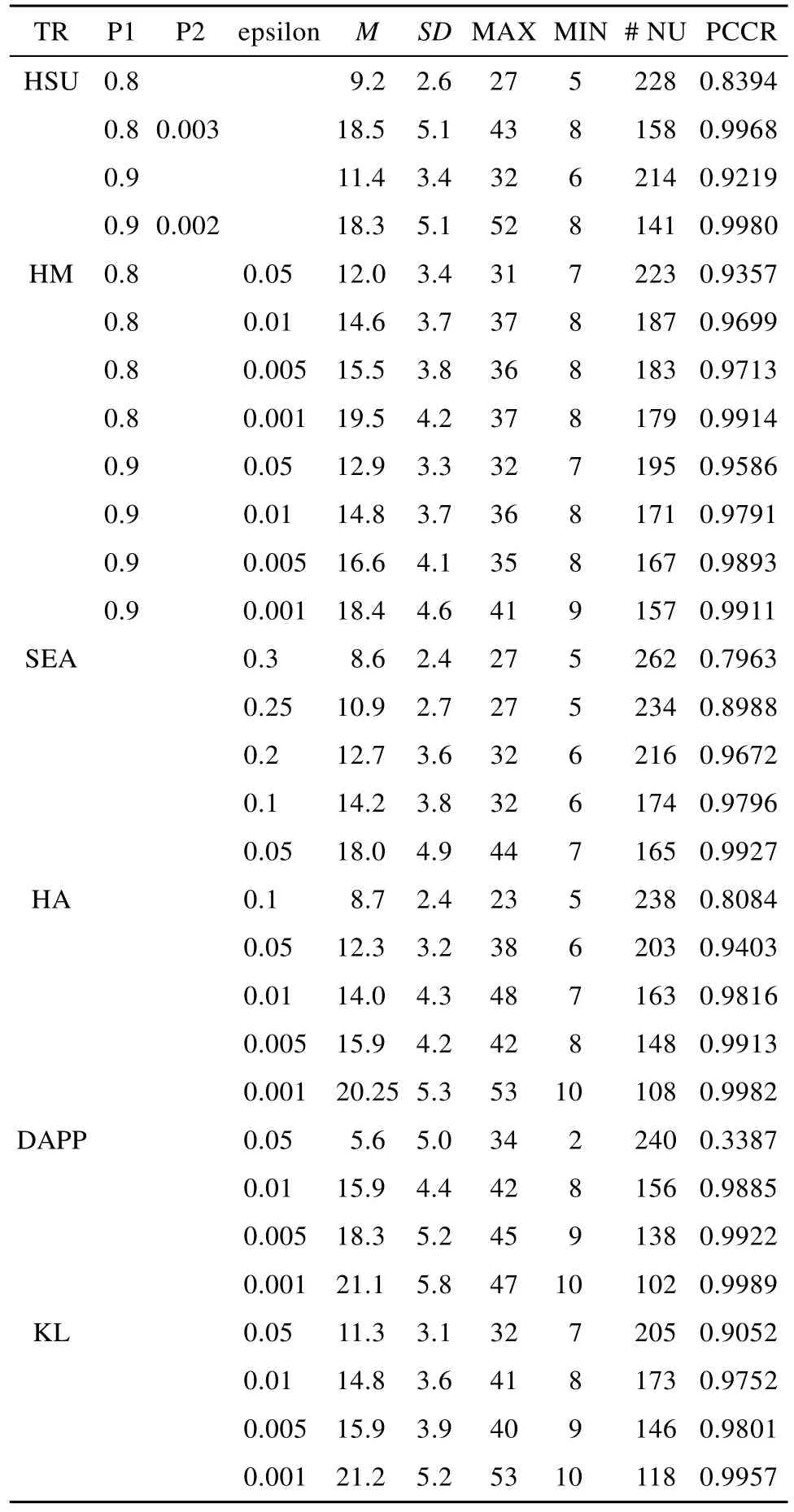
表 1 未加入曝光控制时 6种终止规则的判准率和测验使用情况(30次平均结果)

综上, 本文提出的 4种新的终止规则以及 KL法在测验使用情况和被试模式判准率上的表现均和HSU法相差无几, 表明不论是基于项目水平(HA法)的终止规则, 还是基于被试水平(HSU, DAPP,HM, SEA和KL法)的终止规则, 均能有效地作为变长CD-CAT的终止规则加以使用。

5.2 加入不同曝光控制方法的实验结果与讨论

表2至表4分别为加入simple、MRT和MRP曝光控制方法时, 6种终止规则的模式判准率和测验使用情况。总体来看, 不论采用何种曝光控制方法, 均能很好地控制最大项目曝光率。在绝大部分的实验条件下, 按照精度终止的 PCCR (p)值要高于按照最大测验长度终止的 PCCR (max)值, 这与Hsu等(2013)的研究结果一致。随着P的增大和e的减小, 平均测验长度逐渐增加, 题库中未使用的题目数量逐渐减小(特别地, MRT和MRP法中的未使用题目数量均为0), PCCR (p)值逐渐增加, 按照最大测验长度终止的被试百分比(记作%max)也逐渐增加。在相同实验条件下, 采用不同的曝光控制方法, %max在各个终止规则下是不同的, 甚至在有些终止规则下判准率也有所差异。例如, SEA法在simple条件下的%max最高为14.9 (当e=0.05时),而在MRT和MRP条件下的%max最高分别为65.85和 45.60, 但三者的 PCCR (p)值相差无几, 分别为0.9951, 0.9971和0.9975。HA法在simple条件下的%max最低, 其次是MRP条件下, 最高是MRT条件下, 但三者的PCCR (p)最大值均接近1。而另外一种情况是, KL法在MRP条件下的%max最低, 其次是simple条件下, 最高的%max出现在 MRT条件下, PCCR (p)最大值在simple和MRT条件下均高于 0.98, 但在 MRP条件下 PCCR (p)最大值只有0.7802。这些结果均表明不同的曝光控制方法会以不同的方式和程度影响各个终止规则的表现。

具体来看, 在simple曝光控制下(见表2), 除了DAPP法中e=0.05时, PCCR (p)只有0.3361, 6种终止规则的表现相差无几。在MRT曝光控制下(见表3),DAPP法的表现变得很差, 当e= 0.005时, PCCR (p)值只有0.6438, 而当e=0.001时, PCCR (p)立刻上升至 0.9823, 但%max也已高达 47%左右, 表明DAPP法容易受到MRT方法的影响。在KL法中,有一个特例, 即当e=0.05时, PCCR (p)只有0.3658,但随着e由0.01减小至0.001, PCCR (p)值由0.8395上升至0.9873。在SEA、HA和KL法中, 随着e的减小, PCCR (p)值会逐渐升高, 但%max也逐渐上升, 作者分析其原因可能有两点：第一, e较小对应着比较苛刻的终止条件, 即需要被试作答更多的题目才能满足测验终止的要求; 第二, MRT法在项目曝光率的控制上存在过度控制(overcontrol)现象,即Max (r)值远远小于r= 0.2, 使得质量较好的题目未能提供给被试作答, 从而增加了测验长度。在MRP曝光控制下(见表4), DAPP法的表现依然最差, 即使当e=0.001时, PCCR (p)只有0.6724。在该曝光控制条件下, KL法同样变差, PCCR (p)最大值也只有0.7802。同样地, MRP法在项目曝光率的控制上也存在过度控制现象, 但在相同的实验条件下,%max的比例要比MRT中的小, 而PCCR (p)要稍差于MRT法, 这与Wang等(2011)在定长CD-CAT下的研究结果一致。

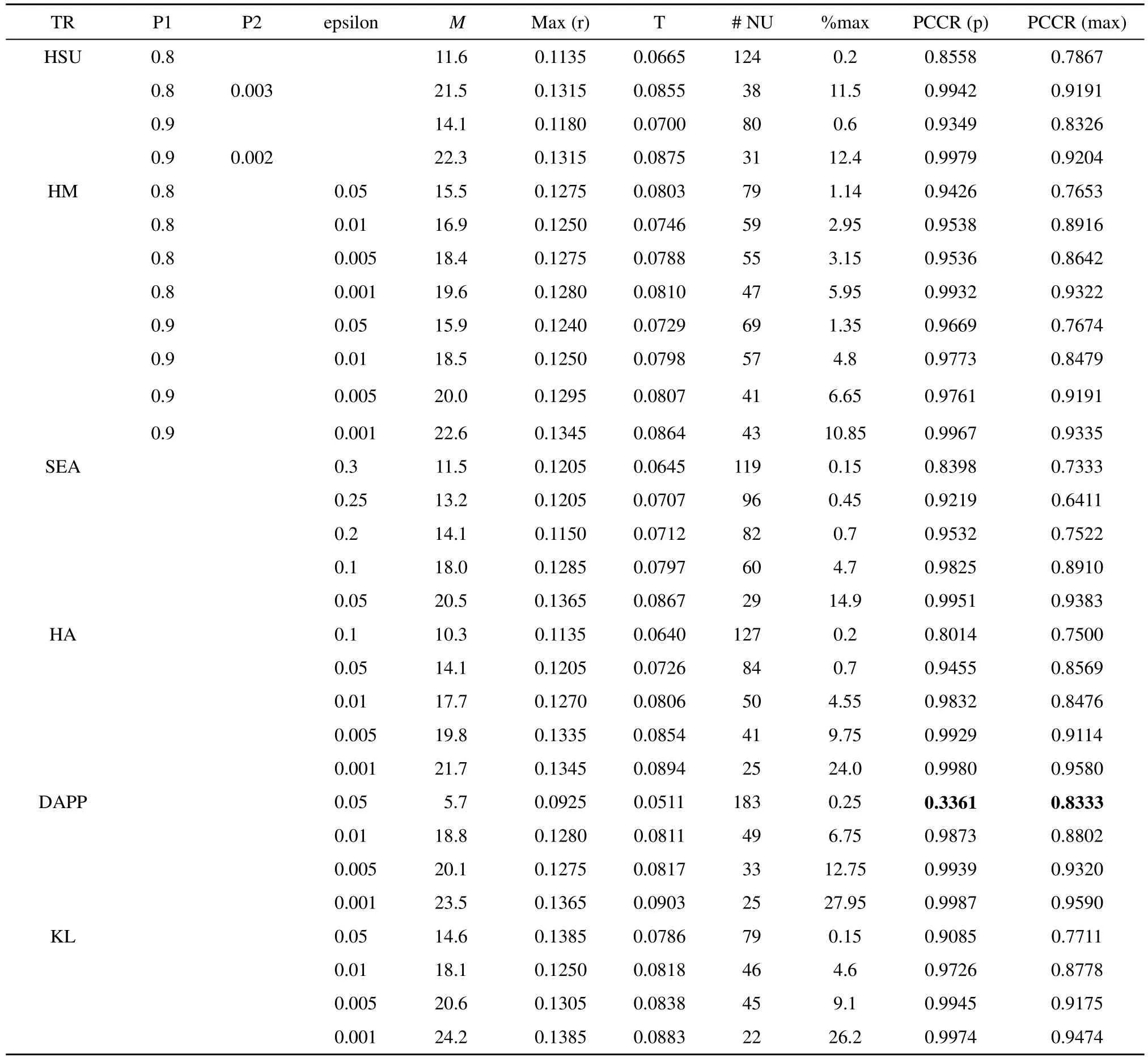
表2 simple曝光控制下6种终止规则的判准率和测验使用情况(30次平均结果)

特别地, 在部分实验条件下, 如表2至表4中粗体部分结果所示, PCCR (max)值要高于PCCR (p)值, 这与大部分实验结果存在矛盾, 这些矛盾的结果主要集中在属于相对标准终止规则的DAPP法和KL法上, 其余从属于绝对标准的终止方法并未出现。这是因为, 相较绝对标准终止规则, 相对标准终止规则并没有设置一个低限临界值(例如, 最大后验概率P至少要高于0.8), 会出现在P未达到0.8之前就符合前后之差低于预设标准(例如,e=0.01), 甚至可能在 P绝对水平很低时就已经符合相对标准而终止测验的情况。例如, 图1和图2分别表示在 DAPP方法(e=0.05)下, 按照精度停止时, 判别正确和判别错误的两个被试的 KS后验概率随测验长度变化的趋势图。每个图中共有2条折线, 分别表示2种知识状态的后验概率。根据DAPP法的思想, 被试 A在作答完 18题后终止测验。其中, 尽管P在测验前期的上升有些波折, 但最终还是上升至0.95附近, 并和其他KS的后验概率拉开了差距。因此, 被试A的KS得到了正确的判别。而被试B在作答完4题后便终止了测验, 表明此时邻近的从属于同一种知识状态的P之差的绝对值小于了预设水平, 但 P的绝对水平仍然很低(只有0.07左右), 并且未能和其他KS的后验概率拉开差距, 因此, 被试B的KS未能得到正确的判别。

表3 MRT曝光控制下6种终止规则的判准率和测验使用情况(30次平均结果)

图3和图4分别表示在DAPP方法(e=0.05)下,按照测验最大长度停止时, 判别正确和判别错误的两个被试的 KS后验概率随测验长度变化的趋势图。被试C在作答前24题时, 有好几条后验概率折线相互纠缠, 导致 KS仍未能分辨清楚。但在作答 25题之后, 其中一条折线迅速上升。当作答至30题时, 该后验概率已超过0.9, 并和其他KS拉开了差距, 因此, 被试C的 KS得到了正确的判别。而被试D在作答完30题后, P的绝对水平只有0.5左右, 没有和其他KS拉开差距, 导致其KS未能得到正确的判别。

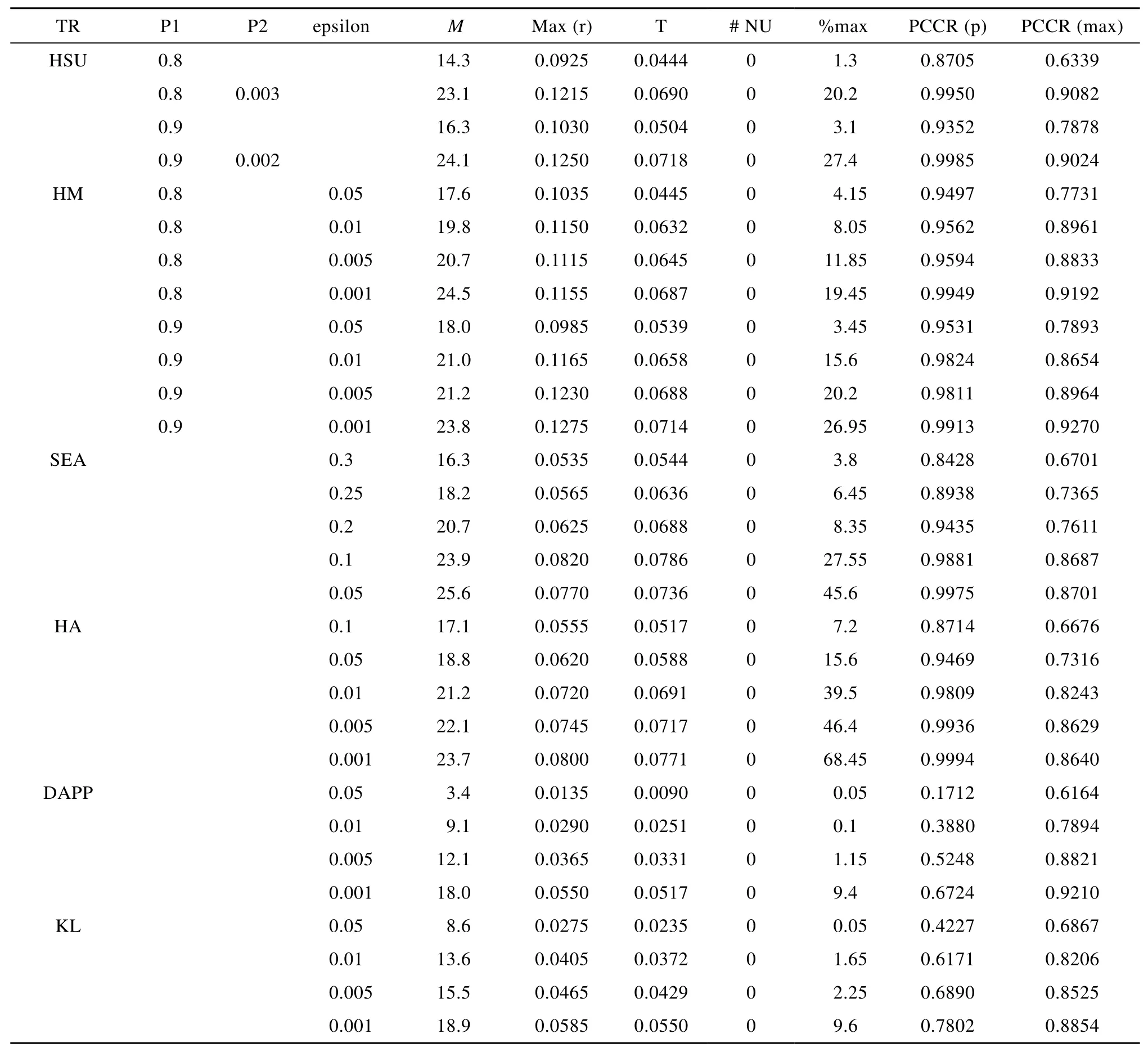
表4 MRP曝光控制下6种终止规则的判准率和测验使用情况(30次平均结果)

图1 被试A的后验概率变化图

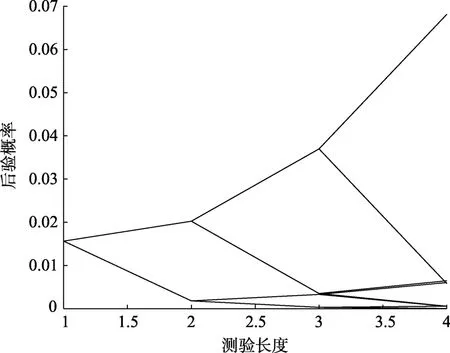
图2 被试B的后验概率变化图

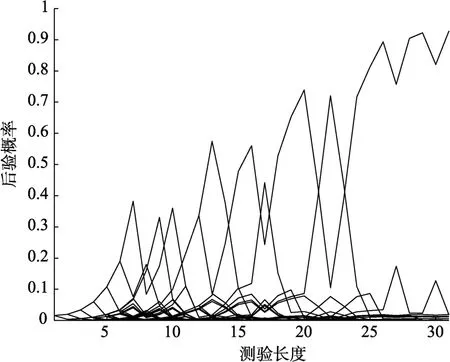
图3 被试C的后验概率变化图

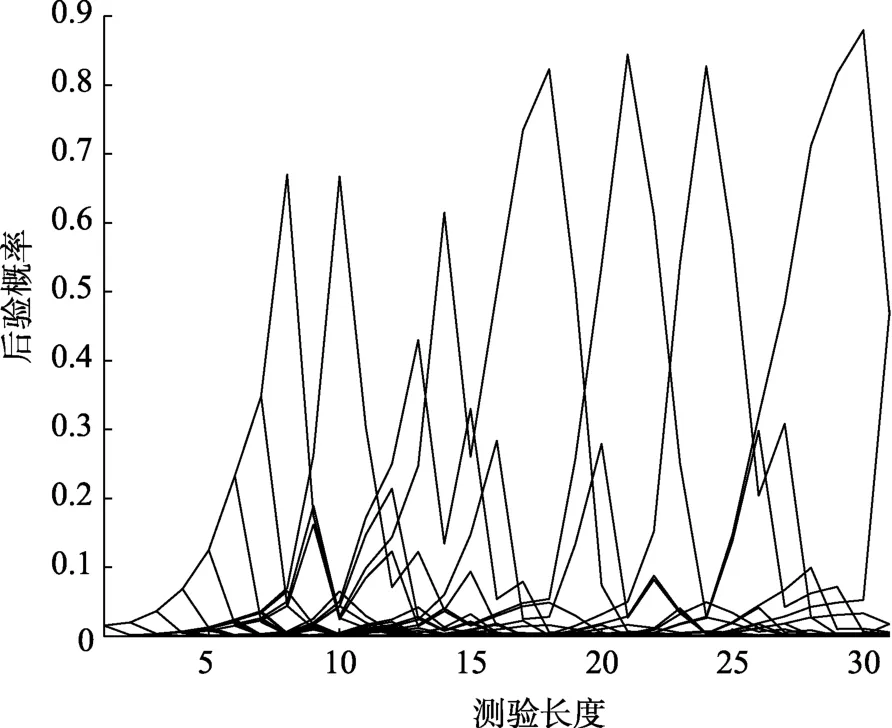
图4 被试D的后验概率变化图

上述结果和分析表明, 曝光控制方法会对相对标准终止规则的表现产生较大影响。

6 结论与展望

CD-CAT结合了认知诊断理论和 CAT的双重优势, 比起传统的测验形式, 它可以更精确、更迅速、更灵活地测量出被试的潜在知识结构, 从而获得被试在知识点上的掌握情况, 为教育教学工作提供有针对性的指导, 促进学生的个性化发展。然而,当前大部分的研究均是以定长 CD-CAT的形式进行研究, 这是由于定长 CD-CAT固定了测验长度,施测较为方便, 但对不同的被试会有不同的测量精度。而自适应测验的精髓应该是使得CD-CAT测验对每个被试的知识状态估计拥有相同的估计精度。与定长 CAT相对应的终止规则为变长(variablelength) CAT, 变长 CAT能够实现每个被试具有相同测量精度的目标, 具有更高的估计精度(Babcock& Weiss, 2009)。

本文提出了 4种新的变长 CD-CAT的终止规则：SEA法、HA法、DAPP法和HM法, 并在未采用曝光控制与采用不同的曝光控制条件下和HSU法以及KL法进行了比较。研究结果表明本文提出的4种新方法能够有效地作为变长CD-CAT的终止规则加以使用。通过模拟研究, 得出的主要结论有：(1)6种变长终止规则均有较好表现, 并且相差无几。终止条件越严格, 平均测验长度越长, 按最大测验长度终止的测验百分比越大, 模式判准率越高。(2)当未加入曝光控制时, 4种新的终止规则均有较好表现, 与HSU法十分接近, 并且随着最大后验概率的增加或e的减小, 模式判准率呈上升趋势, 平均测验长度逐渐增加, 题库中未使用的题目数量逐渐减小, 但在题库使用率方面均较差。(3)当加入项目曝光控制时, 6种变长终止规则下的题库使用率有了极大的提升, 尤其是在MRT和MRP条件下, 题库中未使用的题目数量为 0, 并且仍能保持较高的模式判准率, 但会出现对项目曝光率过度控制的现象。不同的曝光控制方法对各个终止规则的影响是不同的, 其中, 相对标准终止规则极易受到曝光控制方法的影响。(4)结合加入曝光控制后的实验结果来看, SEA、HM以及HA法在各项指标的表现与HSU法基本一致, 其次为KL法和DAPP法。

本研究仍存在一些不足之处, 需要得到进一步地改进和完善。首先, SEA法未能直接对被试知识状态的后验概率进行操作, 而是通过控制每一个属性的边际概率来间接地实现对知识状态后验概率的控制。根据目前的认知诊断理论, 无法求取 KS的标准误, 但属性的边际概率和 KS的后验概率之间存在着一定的数量关系, 属性的边际概率能够确定KS后验概率的一个区间。未来的研究需要进一步提出全新的认知诊断理论, 推导出知识状态的方差, 提出更加直接的CD-CAT变长终止规则。

第二, 题库中的猜测参数g和失误参数s从均匀分布 U (0.05,0.25)中随机抽取。实际上, 根据已有实证研究表明, 参数 g和 s会有较大值出现(de la Torre, 2009; 张启睿, 2012)。在参数波动范围增大的情况下, 6种变长终止规则的表现如何值得研究。

第三, 本研究假设属性之间是独立结构关系,并且固定属性数量为6个。根据已有研究表明, 属性层级还可以包括线型、收敛型、发散型及它们组合起来的更为复杂的结构(Leighton, Gierl, & Hunka,2004), 而且, 实际中的属性层级结构确实是错综复杂的, 并且考察的属性数量通常会多于6个。当属性之间存在层级关系时, 属性之间是否可以通过互借信息的方式来提高判准率, 值得研究。后续研究还需考察在不同的属性层级结构及不同的属性数量下, 6种变长终止规则的表现。

第四, 不同认知诊断模型的假设是不同的, 大体可以分为补偿模型和非补偿模型。在不同类型的诊断模型下, 变长终止规则会有何表现; 不同的题目上限设置(本文为 30题)是否会影响变长终止规则在判准率和测验使用情况上的表现, 是未来的一个研究方向。

第五, 如何将一些非统计约束(Mao & Xin, 2013)纳入到变长CD-CAT的考虑中也值得进一步研究。

Babcock, B., & Weiss, D. J. (2009). Termination criteria in computerized adaptive tests: Variable-length cats are not biased. In D. J. Weiss (Ed.). Paper presented at the Proceedings of the 2009 GMAC Conference on Computerized Adaptive Testing.

Chen, P. (2011). Item replenishing in cognitive diagnostic computerized adaptive testing——based on DINA model (Unpublished doctoral dissertation). Beijing Normal University.

[陈平. (2011). 认知诊断计算机化自适应测验的项目增补——以DINA模型为例 (博士学位论文). 北京师范大学.]

Chen, P., & Xin, T. (2011). Developing on-line calibration methods for cognitive diagnostic computerized adaptive testing. Acta Psychologica Sinica, 43(6), 710–724.

[陈平, 辛涛. (2011). 认知诊断计算机化自适应测验中在线标定方法的开发. 心理学报, 43(6), 710–724. ]

Chen, P., Xin, T., Wang, C., & Chang, H. H. (2012). Online calibration methods for the DINA model with independent attributes in CD-CAT. Psychometrika, 77(2), 201–222.

Cheng, Y. (2008). Computerized adaptive testing—new developments and applications (Unpublished doctoral dissertation).University of Illinois at Urbana-Champaign.

Cheng, Y. (2009). When cognitive diagnosis meets computerized adaptive testing: CD-CAT. Psychometrika, 74(4), 619–632.

Cheng, Y. (2010). Improving cognitive diagnostic computerized adaptive testing by balancing attribute coverage: The modified maximum global discrimination index method.Educational and Psychological Measurement, 70(6), 902–913

Choi, S. W., Grady, M. W., & Dodd, B. G. (2010). A new stopping rule for computerized adaptive testing. Educational and Psychological Measurement, 70(6), 1–17.

de la Torre, J. (2009). DINA model and parameter estimation:A didactic. Journal of Educational and Behavioral Statistics,34(1), 115–130.

Dodd, B. G. (1990). The effect of item selection procedure and stepsize on computerized adaptive attitude measurement using the rating scale model. Applied Psychological Measurement, 14(4), 355–366.

Dodd, B. G., Koch, W. R., & De Ayala, R. J. (1993).Computerized adaptive testing using the partial credit model: Effects of item pool characteristics and different stopping rules. Educational and Psychological Measurement,53(1), 61–77.

Dodd, B. G., De Ayala, R. J., & Koch, W. R. (1995).Computerized adaptive testing with polytomous items.Applied Psychological Measurement, 19(1), 5–22.

Hsu, C. L., Wang, W. C., & Chen, S. Y. (2013). Variablelength computerized adaptive testing based on cognitive diagnosis models. Applied Psychological Measurement,37(7), 563–582.

Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3), 258–272.

Kingsbury, G. G., & Houser, R. L. (1993). Assessing the utility of item response models: Computerized adaptive testing.Educational Measurement: Issues and Practice, 12(1),21–27.

Leighton, J. P., Gierl, M. J., & Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka's rule–space approach. Journal of Educational Measurement, 41(3), 205–237.

Mao, X. Z., & Xin, T. (2011). Improvement of item selection method in cognitive diagnostic computerized adaptive testing. Journal of Beijing Normal University (Natural Science), 47(3), 326–330.

[毛秀珍, 辛涛. (2011). 认知诊断 CAT中选题策略的改进.北京师范大学学报 (自然科学版), 47(3), 326–330. ]

Mao, X. Z., & Xin, T. (2013). A comparison of item selection methods for controlling exposure rate in cognitive diagnostic computerized adaptive testing. Acta Psychologica Sinica,45(6), 694–703.

[毛秀珍, 辛涛. (2013). 认知诊断CAT中项目曝光控制方法的比较. 心理学报, 45(6), 694–703. ]

Mao, X. Z., & Xin, T. (2013). The application of the monte carlo approach to cognitive diagnostic computerized adaptive testing with content constraints. Applied Psychological Measurement, 37(6), 482–496.

Rupp, A. A., Templin, J. L., & Henson, R. A. (2010).Diagnostic measurement: Theory, methods, and applications.Guilford Press.

Tatsuoka, C. (2002). Data analytic methods for latent partially ordered classification models. Journal of the Royal Statistical Society: Series C (Applied Statistics), 51(3), 337–350.

Tatsuoka, C., & Ferguson, T. (2003). Sequential classification on partially ordered sets. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 65(1), 143–157.

Tang, X. J., Ding, S. L., & Yu, Z. H. (2012). Application of computerized adaptive testing in cognitive diagnosis.Advances in Psychological Science, 20(4), 616–626.

[唐小娟, 丁树良, 俞宗火. (2012). 计算机化自适应测验在认知诊断中的应用. 心理科学进展, 20(4), 616–626. ]

Templin, J. L., & Henson, R. A. (2006). Measurement of psychological disorders using cognitive diagnosis models.Psychological Methods, 11(3), 287–305.

Wang, C. (2013). Mutual information item selection method in cognitive diagnostic computerized adaptive testing with short test length. Educational and Psychological Measurement,73(6), 1017–1035.

Wang, C., Chang, H. H., & Douglas, J. (2012). Combining CAT with cognitive diagnosis: A weighted item selection approach. Behavior Research Methods, 44(1), 95–109.

Wang, C., Chang, H. H., & Huebner, A. (2011). Restrictive stochastic item selection methods in cognitive diagnostic computerized adaptive testing. Journal of Educational Measurement, 48(3), 255–273.

Wang, W. Y., Ding, S. L., & You, X. F. (2011). On-line item attribute identification in cognitive diagnostic computerized adaptive testing. Acta Psychologica Sinica, 43(8), 964–976.

[汪文义, 丁树良, 游晓锋. (2011). 计算机化自适应诊断测验中原始题的属性标定. 心理学报, 43(8), 964–976. ]

Weiss, D. J., & Kingsbury, G. (1984). Application of computerized adaptive testing to educational problems.Journal of Educational Measurement, 21(4), 361–375.

Xu, X. L., Chang, H. H., & Douglas, J. (2003). A simulation study to compare CAT strategies for cognitive diagnosis.Paper presented at the annual meeting of the American Educational Research Association, Chicago.

Zhang, Q. R. (2012). Cognitive diagnostic assessment preparation and diagnostic studies on primary school students’ chinese characters learning (Unpublished doctoral thesis). Beijing Normal University.

[张启睿. (2012). 小学低年级学生汉字学习的认知诊断测验编制与诊断研究 (博士学位论文). 北京师范大学.]

Zhang, Q., & Ip, E. H. (2012). Generalized linear model for partially ordered data. Statistics in Medicine, 31, 56–68.