自由下落非均一粒径颗粒流的流场特性

王 怡，樊 航，任晓芬,2

（1西安建筑科技大学环境与市政工程学院，陕西 西安 710055；2 河北工程大学城市建设学院，河北 邯郸 056038）

在工业生产、散装物料运输等过程中，物料从高处下落到地面、料堆、料仓、或传送带时，会有大量颗粒物逃逸至周围空气中，这些游离的颗粒物不仅会对空气造成污染，而且对人体健康和设备安全等产生一系列危害．

为了解决此类问题，前人运用实验和数值模拟方法对自由下落物料进行了研究，研究内容主要集中在卷吸空气量，颗粒流流场特性及产尘量等方面．Hemeon[1]假设颗粒流所受阻力为静止空气中单颗粒的受力之和，得出卷吸空气量表达式．Tooker[2]对Hemeon的理论进行了一定程度的修改，他把颗粒流的整个下落过程视为充分发展的湍流运动，并且引入新的参数来计算卷吸空气量．Cooper和Arnold[3]对卷吸空气量做了进一步的研究而提出了颗粒羽流模型，并且通过实验证明此模型对自由下落颗粒流卷吸量计算的准确性．Liu[4]通过实验给出了一个经验卷吸常数，提出新的两相流模型来预测静止空气中自由下落颗粒的卷吸空气量．Plinke[5-7]等探究了密度、下落高度、含湿量等因素对产尘量的影响，并得出一系列经验公式．Koichiro Ogata[8]用激光测速仪测得均一粒径颗粒流下落的轴心速度，得出轴心处颗粒沉降速度介于真空和受空气阻力的单颗粒速度之间．Renaud Ansart[9]建立了两相流模型计算出流口附近流场，利用PIV技术测试颗粒速度，所得结果预测Liu[4]模型中的速度分布．Uchiyama[10]采用涡方法描述了三种均一粒径颗粒流的自由紊流射流场．王锐[11]等人利用三维格子涡方法模拟了均一粒径颗粒流的速度场．

以上研究表明，已有研究大多以均一粒径颗粒流为对象，关于非均一粒径颗粒流的研究仅存在于对粉尘方面的研究中，对颗粒流流场特性的研究鲜有述及．在工业生产过程中，颗粒物都是以非均一粒径形式存在的，均一粒径颗粒流的流场特性对实际情况有一定的指导意义，但会造成较大的误差．因此，对非均一粒径颗粒流自由下落流场特性的研究非常必要．本文利用DPM-CFD的方法研究非均一粒径自由下落颗粒流周围的气流速度分布、颗粒物的扩散及颗粒速度分布，以期对颗粒流自由下落时颗粒物的污染防治提供一定的参考依据．

1 数学模型

1.1 假设

1） 气体相视为不可压缩的连续相；

2） 颗粒视为球形，密度均匀；

3） 颗粒密度远大于气体密度；

4） 颗粒的体积分数小于10%，忽略颗粒物间的相互碰撞。

1.2 气相模拟

对于假设的不可压缩气体相，忽略体积力，则气相控制方程可以表示为：

连续性方程：

动量方程：

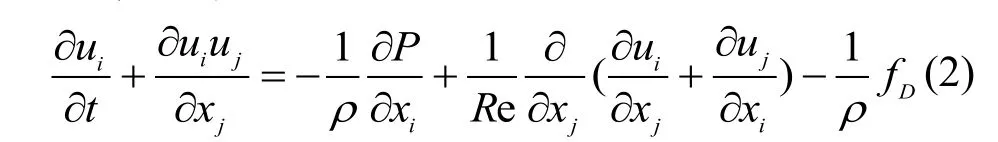
式中：i为x方向节点与界面的标号，j为y方向节点与界面的标号，ui、uj为气相研究节点 i、j方向的速度分量，P为压力，ρ为空气密度，fD为单位控制体积的颗粒作用于气体的阻力．

1.3 颗粒相模拟

颗粒流自由下落过程中，颗粒运动所受的作用力十分复杂，包括重力、气体作用于颗粒的曳力、压力梯度力、虚拟质量力、Magnus力、Saffman力、Basset力等，对于颗粒在湍流气体中所受的轴向力，只考虑曳力即可[12]，其他力可以忽略不计，因此颗粒的作用力平衡方程式：

式中：m为单颗粒的质量，fD为单颗粒在空气中所受阻力，g为重力加速度，uP为颗粒下降速度．

根据上述假设条件，阻力fD可表示为：

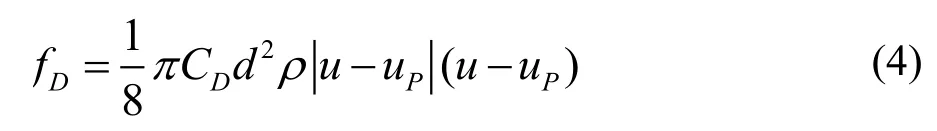
式中：u为空气的速度，CD为颗粒的阻力系数，其表示为：

式中：ReP为颗粒雷诺数，表达式为：

2 物理模型及验证

2.1 物理模型的建立

图1为颗粒流下落计算区域示意图，颗粒物通过宽度为D=0.006 m的条缝释放到静止空气中，控制区为二维的0.8 m×1.5 m的长方形，被离散成9.18万的网格，用来计算颗粒流自由下落的流场特性．

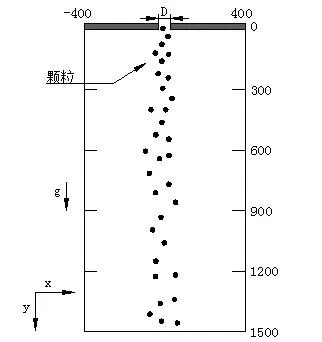
图1 物理模型Fig.1 physical model

2.2 模拟条件

本文数值模拟颗粒入口的边界条件设置为速度入口，空气速度大小为0.001 m/s，左右两侧和底部界面设为自由出流边界．在颗粒下落过程中，颗粒的体积分数小于 10%，故将气相作为连续相考虑，采用标准 k-ε模型，颗粒相的模拟采用 DPM（Discrete Phase Model）模型．颗粒相湍流扩散采用随机轨道模型，并考虑两相之间的耦合．本文所用非均一粒径分布符合Rosin分布，如表1所示，根据Rosin-Rammler方程进行分析计算得到此粒径分布的平均值为300 μm．本文所用均一和非均一粒径颗粒流的计算工况见表 2，颗粒流量设为 0.005 kg/s．

2.3 模型验证

为了验证本文所用数值模拟的可靠性，分别取dp=130 μm和dp=500 μm均一粒径颗粒流进行模拟计算，所得结果分别与文献[9]和[13]进行对比，并绘于图2中.

由图2（a）可以看出：数值模拟值和实验值变值略小于实验值，其原因是实验所用颗粒物的粒径存在一定误差；而且实验所用粉尘颗粒大都不是标准球形，所以会导致颗粒下落时所受曳力较之标准化规律基本一致，平均误差值为10.07%．数值模拟球形颗粒具有一定偏差．总体而言，数值模拟结果和实验结果一致较好．

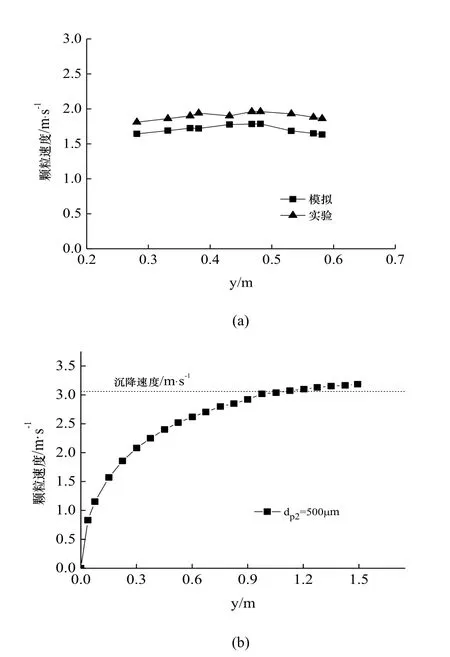
图2 轴线颗粒速度分布Fig.2 The particle velocity distribution in axis line

图2（b）所示，颗粒流下落高度Y＞900时，颗粒速度处于3～3.2 m/s之间，速度变化已经趋近于稳定值．本文引用文献[13]的方法对 dp=500 μm的颗粒自由沉降速度计算如下：

表1 非均一粒径颗粒流粒径分布Tab.1 The size distribution of particles with non-uniform diameter

表2 数据模拟计算参数Tab. 2 calculation parameter of numerical simulation

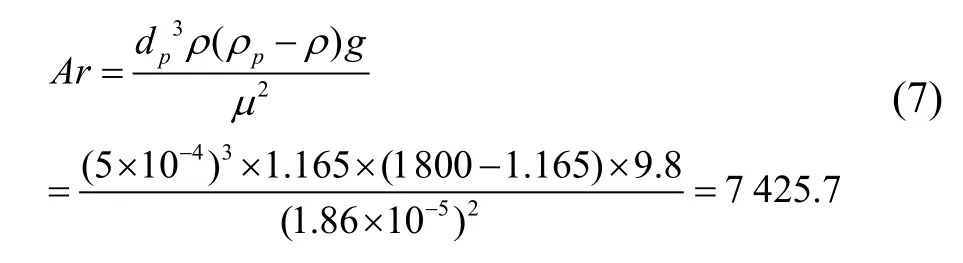
当Ar= 1 .83～3.5×105时，ReP和Ar呈下述关系式:

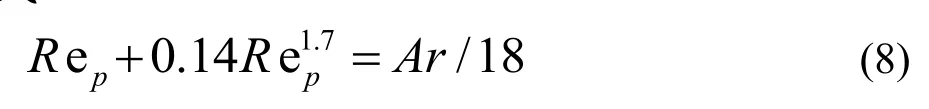
将（7）代入（8）得：ReP=94.5

计算颗粒自由沉降速度ut得：

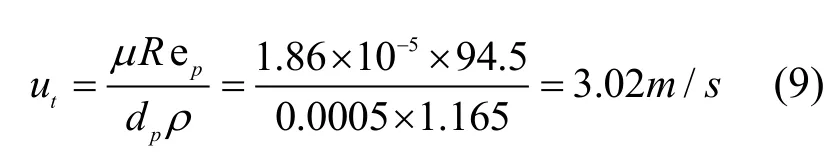
由此可见，模拟得到颗粒自由沉降速度ut与利用前人的计算方法[13]所得结果基本吻合．通过模型验证表明了本文所用模型的准确性．

3 模拟结果与分析

3.1 非均一粒径颗粒流气流速度分布

同横断面的气流分布，且图中速度大小取绝对值．可以看出在不同高度下气流速度变化规律基本相同：气流速度沿径向先减小后增加，随后再次呈现下降趋势，且在轴心处最大；轴心处的气流速度随着高度的增加而增加．在y1=0.2 m处，轴心附近气流速度明显小于下游同位置的气流速度．随着流动进一步发展，气流速度增幅减小．在 y2=0.75 m处，|x|=0.08 m时气流速度发生明显突变，当下落高度达到y3=1.10 m时，气流速度突变发生在|x|=0.12 m处．结合图3可知，此下落距离内有漩涡形成，并且气流速度方向改变．

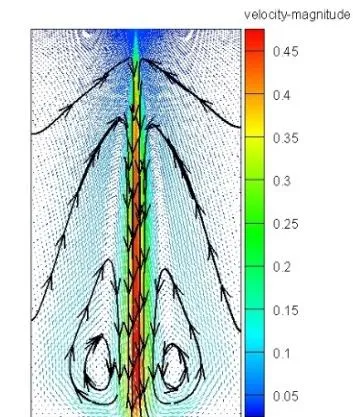
图3 气流速度矢量图Fig.3 The vector graph of airflow velocity

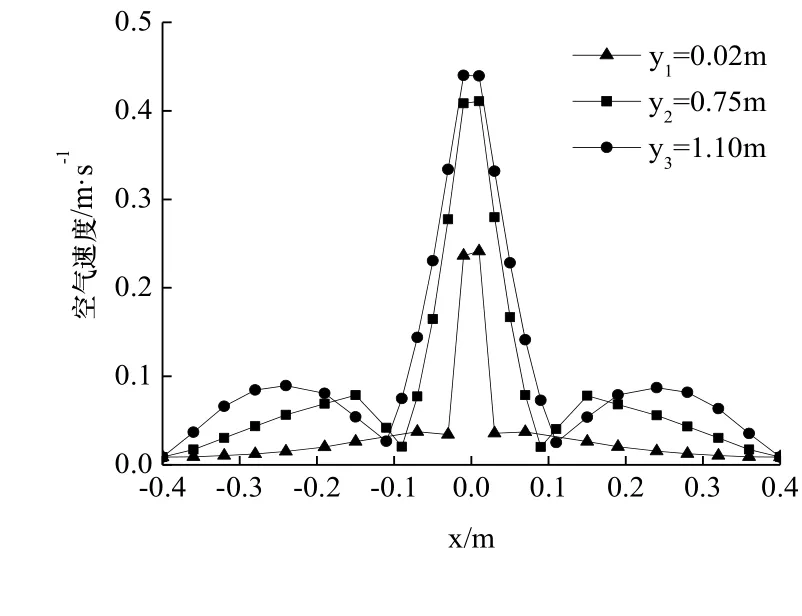
图4 不同断面气流分布Fig.4 The velocity distribution in different secti

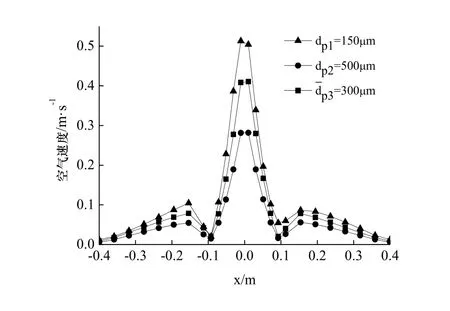
图5 y2=0.75m断面气流分布Fig.5 The velocity distribution in y2=0.75m section

图 5所示为 y2=0.75m各工况断面的气流分布．由图可知，气流速度随颗粒粒径的减小而增大；随着横断面半径的增大，三种工况的气流速度变化趋势相同．这是由于相同流量下，随着粒径的增大，单位时间下落的颗粒数减少，颗粒与空气的接触面减小，从而使颗粒对气流的影响减弱．非均一粒径颗粒流的气流速度介于dp1=150 μm和dp2=500 μm均一粒径颗粒流之间．

3.2 非均一粒径颗粒流扩散浓度

图6显示，在非均一粒径颗粒流自由下落过程中，颗粒物浓度沿径向逐渐减小，且扩散范围随着下落距离的增大而增加．y2=0.75 m和y3=1.10 m处轴心的颗粒物浓度远远小于y1=0.2 m处轴心的浓度，y1=0.2 m处扩散半径仅为0.01 m，而达到y3=1.10 m时，扩散半径显著增大到0.07 m．该现象产生的原因是：随着下落距离的增大，周围空气被不断卷入颗粒流中，颗粒间隙率增大，因而造成扩散半径逐渐增大．

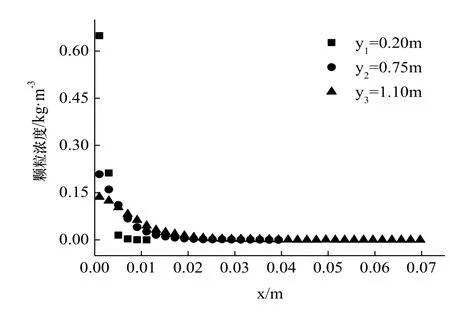
图6 不同断面颗粒浓度Fig.6 The particle concentration in different section

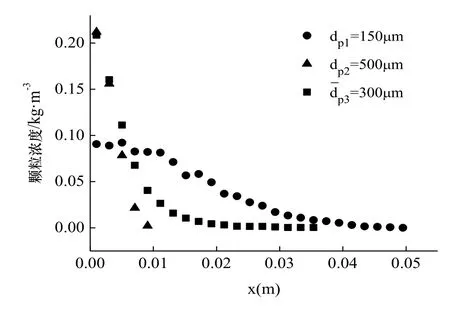
图7 y2=0.75m断面颗粒浓度Fig.7 The particle concentration in y2=0.75m section

图7所示y2=0.75m各工况下颗粒流浓度沿径向的变化规律，由图可知，扩散半径受颗粒流粒径的影响非常显著，粒径越小，扩散半径越大．根据数据分析，此断面上dp1=150 μm的均一粒径颗粒流扩散半径为=300 μm 的非均一粒径颗粒流的 1.5倍．当x≥0.005 m时，与dp1=150 μm的均一粒径颗粒流相比较，非均一粒径颗粒流的颗粒物浓度反而较小．

3.3 非均一粒径颗粒流颗粒速度分布

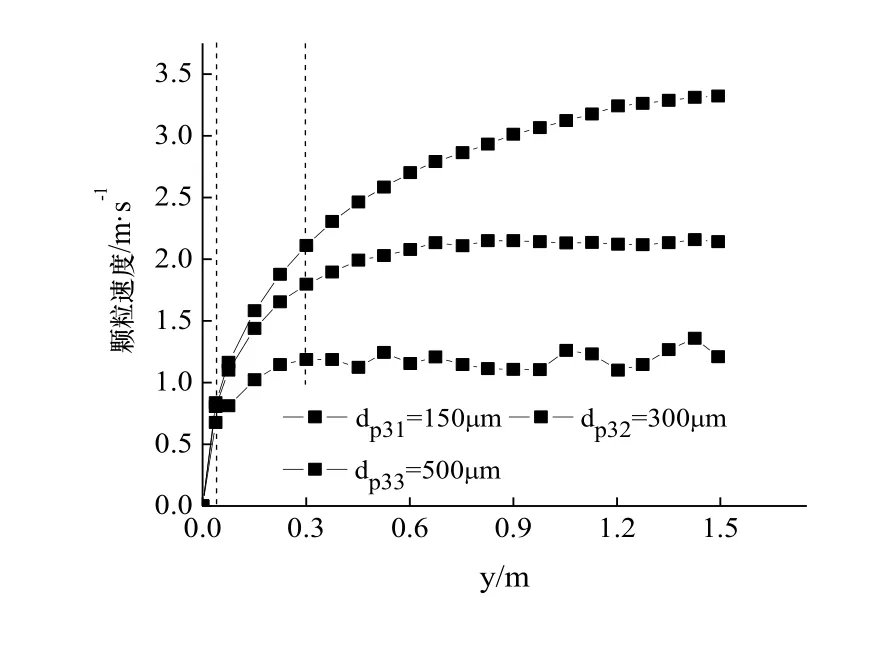
图8μm非均一粒径的颗粒速度分布Fig.8 Particle velocity distribution of non-uniformsize when=300μm

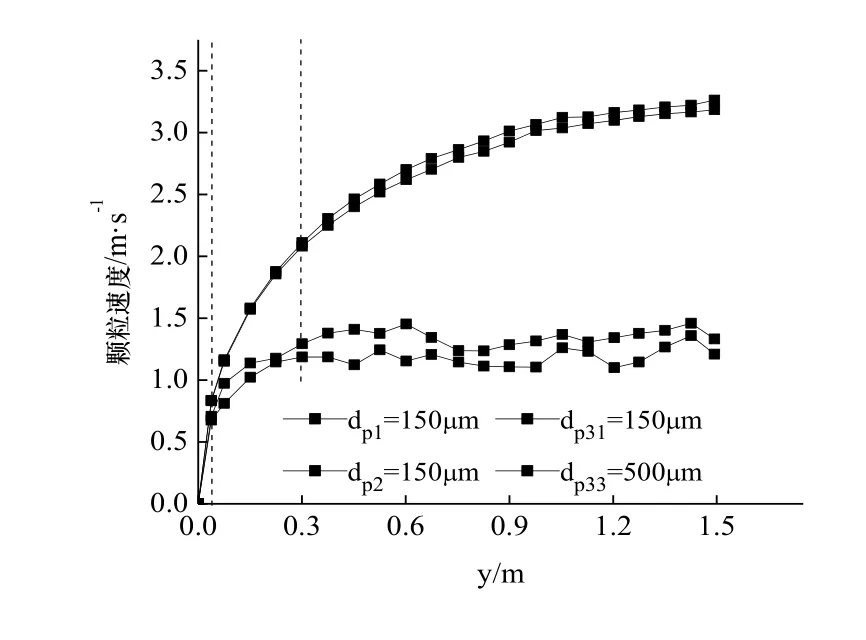
图9 不同工况同粒径的颗粒速度分布Fig.9 Particle velocity distribution of uniform size in different cases

图9将非均一粒径工况和均一粒径工况进行比较，可以看出均一粒径与非均一粒径颗粒流中 500 μm 的颗粒速度分布基本一致，而非均一粒径工况的150 μm颗粒速度比均一粒径工况小，且后者约为前者的1.13倍．原因是处于非均一颗粒流边缘的小粒径颗粒浓度相比150 μm均一粒径颗粒流浓度较小，颗粒体积分数减小，作用在每个颗粒上的空气摩擦力增加，导致颗粒速度减小．

根据上述分析，由扩散半径和颗粒沉降速度的变化情况可知，非均一粒径颗粒流中大颗粒对小颗粒的扩散半径和沉降速度均有影响，且对扩散半径影响更大．

4 结论

为了考察自由下落非均一粒径颗粒流的流场特性，本文采用数值模拟方法对颗粒与空气耦合作用下的气流速度分布、颗粒扩散规律以及颗粒速度分布进行了研究，得出以下结论：

(1)颗粒流下落会导致空气沿垂直方向形成向下的射流；在本文研究范围内，射流两侧出现漩涡，且漩涡覆盖y2=0.75 m和y3=1.10 m两处；气流速度随着颗粒粒径的增大而减小．

(2)颗粒物浓度沿径向逐渐减小，且扩散范围随着下落距离的增大而增加；在同一高度，粒径越小，颗粒流扩散半径越大，y2=0.75 m时dp1=150 μm的颗粒流扩散半径为d—p3=300 μm扩散半径的1.5倍．

(3)颗粒流自由下落时，颗粒速度的增幅由快到慢，逐渐趋于平缓；与均一粒径相比，非均一粒径下的同粒径小颗粒具有更小的沉降速度，因此小粒径颗粒流中混入大颗粒可使其沉降速度减小．

References

[1] HEMEON W C L. Plant and process ventilation[M]//Plant and process ventilation. Industrial Press, 1963: 120-161.

[2] TOOKER G E. Controlling fugitive dust emissions in material handling operations[J]. Bulk Solids Handling,1992, 12(2): 227-32.

[3] COOPER P, ARNOLD P. Air entrainment and dust generation from a falling stream of bulk material[J].KONA Powder and Particle Journal, 1995, 13(0):125-134.

[4] LIU Z Q. Air entrainment in free falling bulk materials[D]. University of Wollongong, 2001.

[5] PLINKE M A E, LEITH D, HOLSTEIN D B, et al.Experimental examination of factors that affect dust generation[J]. The American Industrial Hygiene Association Journal, 1991, 52(12): 521-528.

[6] PLINKE M A E, MAUS R, LEITH D. Experimental examination of factors that affect dust generation by using Heubach and MRI testers[J]. The American Industrial Hygiene Association Journal, 1992, 53(5):325-330.

[7] PLINKE M A E, LEITH D, BOUNDY M G, et al. Dust generation from handling powders in industry[J].American Industrial Hygiene Association, 1995, 56(3):251-257.

[8] OGATA K, FUNATSU K, TOMITA Y. Experimental investigation of a free falling powder jet and the air entrainment[J]. Powder technology, 2001, 115(1): 90-95.

[9] ANSART R, RYCK de A, DODDS J A, et al. Dust emission by powder handling: comparison between numerical analysis and experimental results[J]. Powder Technology, 2009, 190(1): 274-281.

[10] UCHIYAMA T. Numerical analysis of particulate jet generated by free falling particles[J]. Powder technology,2004, 145(2): 123-130.

[11] 王锐, 陈斌. 三维格子涡方法模拟自由下落颗粒群[J].工程热物理学报, 2014, 35(3): 499-502.WANG Rui, CHEN Bin. Numerical simulation of free falling particles by three-dimensional vortex-in-cell method[J]. Journal of Engineering Thermophysics, 2014,35(3): 499-502.

[12] 施学贵,徐旭常,冯俊凯. 颗粒在湍流气流中运动的受力分析[J]. 工程热物理学报,1989, 10(3): 320-325.SHI Xuegui, XU Xuchang, FENG Junkai. The analysis of forces on particles moving in turbulent flow[J]. Journal of Engineering Thermophysics, 1989, 10(3): 320-325.

[13] 王宝和, 王喜忠. 计算球形颗粒自由沉降速度的一种新方法[J]. 粉体技术, 1996, 2(2): 30-39.WANG Baohe, WANG Xizhong. New method for calculation of settling velocity of a spherodial particle[J].Powder Science and Technology, 1996, 2(2): 30-39.