方钢管混凝土框架-单侧开洞薄钢板剪力墙滞回性能研究
2015-01-23王先铁王东石李海广贾贵强刘立达
王先铁,王东石,李海广,贾贵强,刘立达
(1. 西安建筑科技大学土木工程学院,陕西 西安710055;2. 烟台市建筑设计研究股份有限公司,山东 烟台 264003)
方钢管混凝土框架具有承载力高、延性好、耗能能力强等优点.薄钢板墙能充分利用钢板墙的屈曲后强度,依靠拉力带抵抗水平荷载,具有自重轻、延性好、抗震性能优异和经济性好等优点.将抗震性能优异的薄钢板剪力墙与方钢管混凝土框架结合,可以充分发挥二者的结构特性,形成了具有优异力学性能的方钢管混凝土框架-薄钢板剪力墙结构[1-5].以往对于薄钢板墙的研究,多集中于H型钢作为竖向边缘构件,但是H型钢柱易发生屈曲而导致结构整体失效[6].采用方钢管混凝土柱作为薄钢板剪力墙的竖向边缘构件,易满足薄钢板剪力墙对竖向边缘构件较高的强度和刚度需求,有效避免薄钢板剪力墙竖向边缘构件易过早失效而影响钢板墙性能的问题,符合“强框架,弱墙板”的设计要求,有利于双重抗震设防目标的实现[5].
由于钢板墙较多的应用在高层建筑的核心筒和电梯井中,在钢板墙中设置安装设备管线的管洞必不可少,尤其当钢板墙处于电梯及楼梯间的出入口时要留有门、窗洞口以满足使用要求.Vian[7]等对开洞钢板墙进行了试验研究和有限元分析,结果表明,开设洞口在满足使用要求的基础上并不会过多降低钢板剪力墙结构的抗侧承载力和延性.Sabouri-Ghomi[8]等对开洞钢板剪力墙的抗震性能进行了数值分析,结果表明,加劲与非加劲开洞钢板剪力墙耗能能力随开洞率的增加而降低,开洞率对非加劲钢板墙的影响较大.郝际平[9]等对两片侧边开洞钢板墙进行了拟静力试验研究,指出钢板墙开洞可以减小内填板宽度,调整内填板与框架的刚度比.聂建国等[10-12]对3个4层1/5比例的钢板剪力墙试件进行了拟静力试验研究,分析了钢板墙开洞对其性能的影响,基于试验结果提出了开洞钢板剪力墙的抗侧承载力计算模型和计算公式.综上所述,开洞可以调节钢板墙与框架刚度比,但会降低钢板墙的刚度、承载力和耗能性能.以往研究中竖向边缘构件大多为H型钢,对采用方钢管混凝土柱作为竖向边缘构件的开洞钢板墙研究较少.
本文进行了一榀1/3比例单跨两层方钢管混凝土框架-单侧开洞薄钢板剪力墙的低周往复荷载试验,采用有限元软件 ABAQUS对其进行了数值分析,研究了框架柱截面类型、开洞率δ、内填钢板墙高厚比β、柱子抗弯刚度η和轴压比n等对方钢管混凝土框架-单侧开洞薄钢板墙滞回性能的影响,分析了其承载力、滞回性能和刚度的变化规律.
1 试验研究
1.1 试件设计
设计了1榀1/3比例单跨两层方钢管混凝土框架-单侧开洞薄钢板剪力墙试件,如图1所示.内填钢板墙厚度为3 mm.参考文献[13]确定边框尺寸,方钢管截面为□200×6,内灌C30混凝土,底梁和顶梁截 面 为 H300×150×10×12 , 中 梁 截 面 为H200×100×10×12.洞口周围钢板墙两侧设置[5通长加劲肋.框架内周边设置﹣6 mm×60 mm的鱼尾板,钢板墙与鱼尾板采用双面交替间断角焊缝连接.梁柱采用栓焊连接,节点区钢管内设置内隔板.所有钢材均为Q235B,钢材材性试验结果见表1.方钢管柱内混凝土立方体抗压强度实测值33.9 N/mm2.
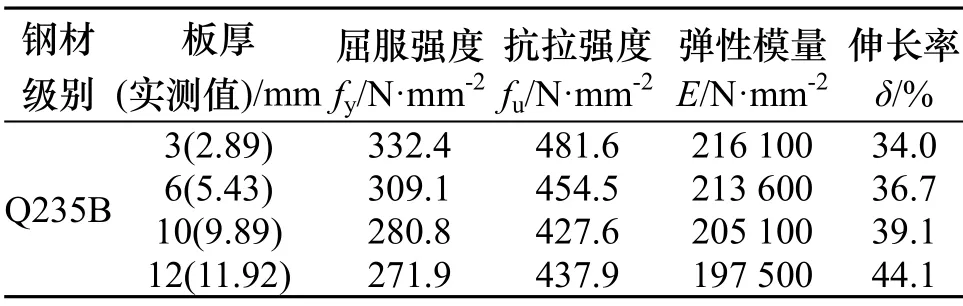
表1 钢材材性试验结果Tab.1 Material results of steel

图2 试验装置Fig.2 Test setup

图1 试件尺寸Fig.1 Dimensions of specimen
1.2 试验装置及加载制度
试验装置如图2所示.通过两个带滚轴且顶部可单向转动的200 t千斤顶在柱顶施加400 kN竖向荷载.通过两个100 t MTS作动器施加水平往复荷载.作动器与顶梁上部专用水平加载装置连接,可避免试件整体扭转及传统梁端加载的不对称.在每层框架柱两侧设置带轴承的侧向支撑,防止试件面外失稳.水平荷载采用荷载-位移混合控制的加载制度[14].试件屈服前,采用荷载控制加载,以100 kN增量为一级,每级循环一周.400 kN以后每级增量为50 kN,每级循环一周;试件屈服后改为位移控制加载,每级增量为0.5倍屈服位移Δy,每级循环三周.
1.3 测试内容和测点布置
利用应变片、位移计和百分表监测试件在低周往复加载过程中的受力与变形情况,位移计和应变片布置如图3所示.在每层梁的两端各布置1个位移计测量试件的水平位移,在地梁端部布置1个电子百分表监测地梁水平位移.梁柱节点处设置斜向位移计测量梁柱节点相对转角.在梁柱节点区中心和钢梁两端腹板布置应变花,钢梁两端上下翼缘布置应变片,用于监测边缘构件的应力发展情况.在钢板墙中部、角部以及其它应力较大的位置布置应变花和应变片,以监测钢板墙的应力发展过程.

图3 测点布置Fig.3 Layout of measuring points
1.4 试验过程及主要现象
推向至300 kN时,两层钢板墙均产生面外屈曲变形.反向加载时,钢板墙出现“呼吸效应”.拉向至400 kN时,一、二层钢板墙沿对角线处屈服(最大应变1 644με).推向至450 kN时,两层钢板墙沿对角线方向形成多道屈曲半波和拉力带,滞回曲线明显向位移轴倾斜,取屈服位移Δy为24 mm.此时,一、二层钢板墙最大面外变形分别为20、16 mm.1.5Δy位移时,一层槽钢加劲肋底部焊缝开裂(图4a).由于钢板墙角部应力集中,一层下部鱼尾板东侧与底梁上翼缘焊缝被拉裂.2.0Δy加载完成时,二层槽钢加劲肋顶部焊缝被拉断(图4b),西柱柱脚轻微鼓曲.第三循环推向完成时,二层钢板墙西北角沿对角线方向撕裂(图4c),中梁东侧腹板和东柱柱脚鼓曲.第三循环拉向完成时,二层钢板墙中心被撕裂.2.5Δy时试件达到峰值荷载,此时,一、二层钢板墙最大面外变形分别为40、28 mm.随着循环位移增大,鱼尾板与框架间的裂缝、钢板墙角部及中部裂缝继续发展.由于一层槽钢加劲肋端部焊缝断裂,对钢板墙拉力场锚固作用减弱,试件承载力逐渐下降.钢板墙中心撕裂(图4d),中梁东端下翼缘与柱壁焊缝撕裂(图 4e).3.0Δy位移第一循环拉向完成时,二层鱼尾板与顶梁下翼缘焊缝撕裂,顶梁东端下翼缘与柱壁焊缝被拉断.第二循环拉向完成时,二层槽钢加劲肋底部与中梁上翼缘焊缝被拉断(图4f).3.5Δy位移第一循环推向完成时,水平荷载降至峰值荷载的 85%以下,试验结束.最终破坏形态见图4g.

图4 试验现象Fig.4 Experiment phenomena
1.5 试验结果
试件的水平荷载-顶点位移滞回曲线如图 5所示.达到峰值荷载前,滞回环呈饱满的梭形.随着位移增加,滞回环由梭形转化为反S形.由于钢板墙侧边开洞,减小了钢板墙宽度,降低了钢板墙与边框架的刚度比.此外,洞口边缘加劲肋在一定程度上限制了钢板墙的面外变形,因此,试件滞回曲线的“捏缩”较小.

图5 荷载-位移滞回曲线Fig.5 Load-displacement hysteretic curves
试件的一层层间位移为35.38 mm(层间位移角1/40),二层层间位移为 46.99 mm(层间位移角1/30),均大于《建筑抗震设计规范》(GB50011-2010)[15]中多、高层钢结构弹塑性层间位移角 1/50的限值,试件推、拉方向的延性系数分别为3.89、4.22,表明试件具有良好的延性.
11 .6 破坏机理
在较小的水平荷载作用下,主压应力方向的钢板墙即发生屈曲,对角线方向形成拉力带.随着位移增加,拉力带沿对角线逐渐向外扩展,钢板墙屈服面积逐渐增大,钢板墙角部和中部在水平往复荷载作用下形成折褶,最终撕裂,之后荷载主要由框架承担.梁端与柱壁焊缝逐渐开裂,最终由于柱脚产生塑性铰,试件破坏.试件破坏过程为钢板墙先屈曲、后屈服,随后钢管混凝土柱脚形成塑性铰而破坏.符合“钢板墙先于框架破坏”的抗震设防理念,达到双重设防目标.
由于钢板墙侧边开洞,开洞侧槽钢加劲肋相当于局部边缘构件,为钢板墙屈曲后拉力场提供锚固作用.当槽钢加劲肋与周边框架的焊缝破坏后,局部边缘构件对钢板墙拉力场的锚固作用减弱,导致后期钢板墙拉力场未能充分开展,影响了试件承载能力和延性的充分发挥.因此,为了充分发挥侧边开洞钢板墙的屈曲后性能,必须确保洞口边缘加劲肋具有足够的强度和刚度,以及加劲肋两端与周边框架的可靠连接.
2 数值分析与试验结果对比
2.1 有限元模型
采用有限元软件 ABAQUS对试件进行数值分析.钢材材性参数取材性试验结果,泊松比为0.30.梁柱和钢板墙选用线性减缩薄壳单元 S4R,混凝土选用八节点缩减积分格式的实体单元C3D8R.考虑几何非线性、材料非线性及接触非线性.混凝土应力-应变关系采用考虑钢管约束效应的核心混凝土应力-应变关系模型[16],考虑混凝土的塑性损伤[17],其材料塑性参数取值见表2.钢管壁与混凝土之间沿法线方向采用“硬”接触,切线方向采用库伦摩擦模型,摩擦系数取0.6,以考虑二者间的粘结滑移.通过限制柱脚平面各个方向的位移和转角,模拟嵌固边界条件;限制钢梁面外水平位移,防止钢梁过早发生平面外失稳.有限元模型如图6所示.

表2 混凝土塑性参数Tab.2 Plastic coefficients of concrete

图6 有限元模型Fig.6 Finite element model
2.2 结果对比
试验与有限元计算滞回曲线和骨架曲线如图 7所示.加载初期,试件处于弹性阶段,骨架曲线接近直线,有限元结果与试验吻合较好.试件屈服后,钢板墙大部分屈服,刚度逐渐降低,随着位移增大,钢板墙开洞一侧槽钢加劲肋与框架梁之间焊缝断裂,降低了对钢板墙拉力场的锚固.峰值荷载后,钢板墙分担水平荷载的比例减少,框架分担水平荷载的比例增加.在试验滞回曲线的荷载下降段,水平荷载主要由框架承担,荷载与刚度均下降较快.
有限元模拟了试件的理想情况,而材料强度的离散性、试件加工质量、试验装置间的缝隙、支撑系统对试件的摩擦力等因素都将对结构性能产生影响.同时ABAQUS中的金属本构模型未能考虑材料在循环荷载下的损伤与断裂.因此试验滞回曲线呈反“S”型,而有限元计算滞回曲线较为饱满,“捏缩”相对较轻,有限元骨架曲线在达到峰值荷载后,未出现明显下降段.虽然有限元结果与试验结果数值略有差距,但有限元模拟较好地反映了试件承载力、变形、受力机理等在往复荷载作用下发展的全过程.

图7 试验与有限元结果比较Fig.7 Comparison of the test and finite element results
3 滞回性能参数分析
3.1 分析模型的建立
分析模型几何尺寸以试验试件为基准.钢材选用 Q235,屈服强度 fy=235 N/mm2,钢材弹性模量Es=2.06×105N/mm2.采用弹性-线性强化模型,强化模量Et=0.02Es.混凝土标号为C40,标准抗压强度fc=26.8 N/mm2,弹性模量 Ec=3.25×104N/mm2,考虑钢管对混凝土的约束效应及混凝土材料塑性损伤.
3.2 分析参数的确定
在基本模型的基础上,研究的主要参数为:边框柱截面类型、开洞率 δ、钢板墙高厚比 β、柱子抗弯刚度η和轴压比n.
为研究边框柱截面类型对滞回性能的影响,设计了两个模型,其编号分别为SC和S,SC模型的边框柱截面为□200×6,S模型的边框柱截面根据柱子刚度系数相等的原则将基本模型的方钢管混凝土柱换算为工字型截面钢柱(H150×150×8×14)[18],其中钢管混凝土柱截面EI和EA的计算参照文献[19]的规定.为保证拉力场的充分开展,边框柱必须具有一定的抗弯刚度,为比较钢管混凝土柱抗弯刚度对滞回性能的影响,定义“柱抗弯刚度系数η=(EI)sc/(EI)min”,其中(EI)sc为钢管混凝土柱抗弯刚度,参照文献[19]计算,(EI)min为钢管混凝土柱最小抗弯刚度,参照文献[20]计算.开洞率 δ为洞口宽度与梁净跨的比值,开洞率 δ取值为 0.04~0.5,钢板墙高厚比β取值为300~600,柱子轴压比n 取值为 0.4~0.8.
3.3 各参数对滞回性能的影响
3.3.1 边框柱截面类型对滞回性能的影响
图8为边框柱截面类型对滞回性能的影响.在柱子刚度系数相同的条件下,SC模型的滞回曲线完全包围了S模型的滞回曲线,表明SC模型的整体滞回性能优于S模型.SC模型的承载力远高于S模型,提高约28%.与工字形钢柱相比,作为钢板墙竖向边缘构件的钢管混凝土柱,具有良好的承载力和抗侧刚度.当层间位移角未达到0.012 rad时,即未达到极限荷载时,二者滞回环面积变化曲线基本重合,表明此时二者能量耗散量相同;当层间位移角超过0.012 rad时,SC模型的滞回环面积变化曲线明显高于S模型,表明此时SC模型的能量耗散量远高于S模型.随着层间位移角的增加,S模型各阶段的能量耗散系数均大于SC模型,表明S模型的能量耗散效率高于SC模型.SC模型各阶段的刚度均高于S模型且初始刚度相差尤为明显,SC模型的刚度退化较S模型缓慢.
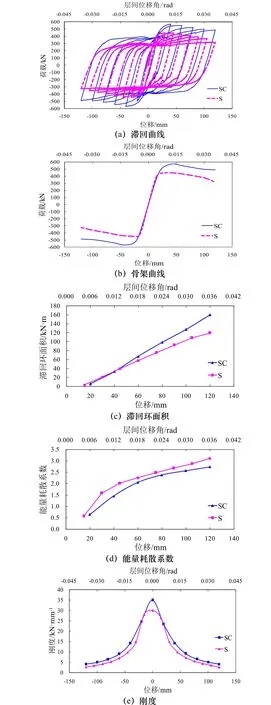
图8 柱截面类型对滞回性能的影响Fig.8 Influence of column section type on hysteretic behavior
3.3.2 开洞率δ对滞回性能的影响
图 9分别为不同开洞率单侧开洞钢板剪力墙的骨架曲线、滞回环面积曲线、能量耗散系数曲线和刚度曲线.随着开洞率的增大,单侧开洞钢板剪力墙承载力降低,当开洞率δ=0.04时,承载力最大约为744 kN(正向)和764 kN(负向),当开洞率δ=0.5时,承载力最小约为546 kN(正向)和550 kN(负向).由此可知,框架跨度一定时,开洞率增大会导致钢板墙宽度减少,进而使钢板墙侧向承载力降低且影响显著.开洞率越大,滞回环面积越小,结构耗能量越少.当开洞率δ=0.1和δ=0.2时,滞回环面积曲线基本重合.层间位移角未达到0.024 rad时,开洞率δ=0.2时能量耗散系数最大,开洞率δ=0.5时能量耗散系数最小,表明开洞率δ=0.2时,单侧开洞钢板剪力墙耗能最好.开洞率越大,初始刚度越小,当开洞率δ从0.04增大到0.2时,初始刚度降低幅度最小且开洞率δ=0.1和δ=0.2的刚度曲线基本重合,表明开洞会显著降低单侧开洞钢板剪力墙的初始刚度.

图9 开洞率对滞回性能的影响Fig.9 Influence of opening ratio on hysteretic behavior
3.3.3 钢板墙高厚比β对滞回性能的影响
图 10分别为不同高厚比单侧开洞钢板剪力墙的骨架曲线、滞回环面积曲线、能量耗散系数曲线和刚度曲线.
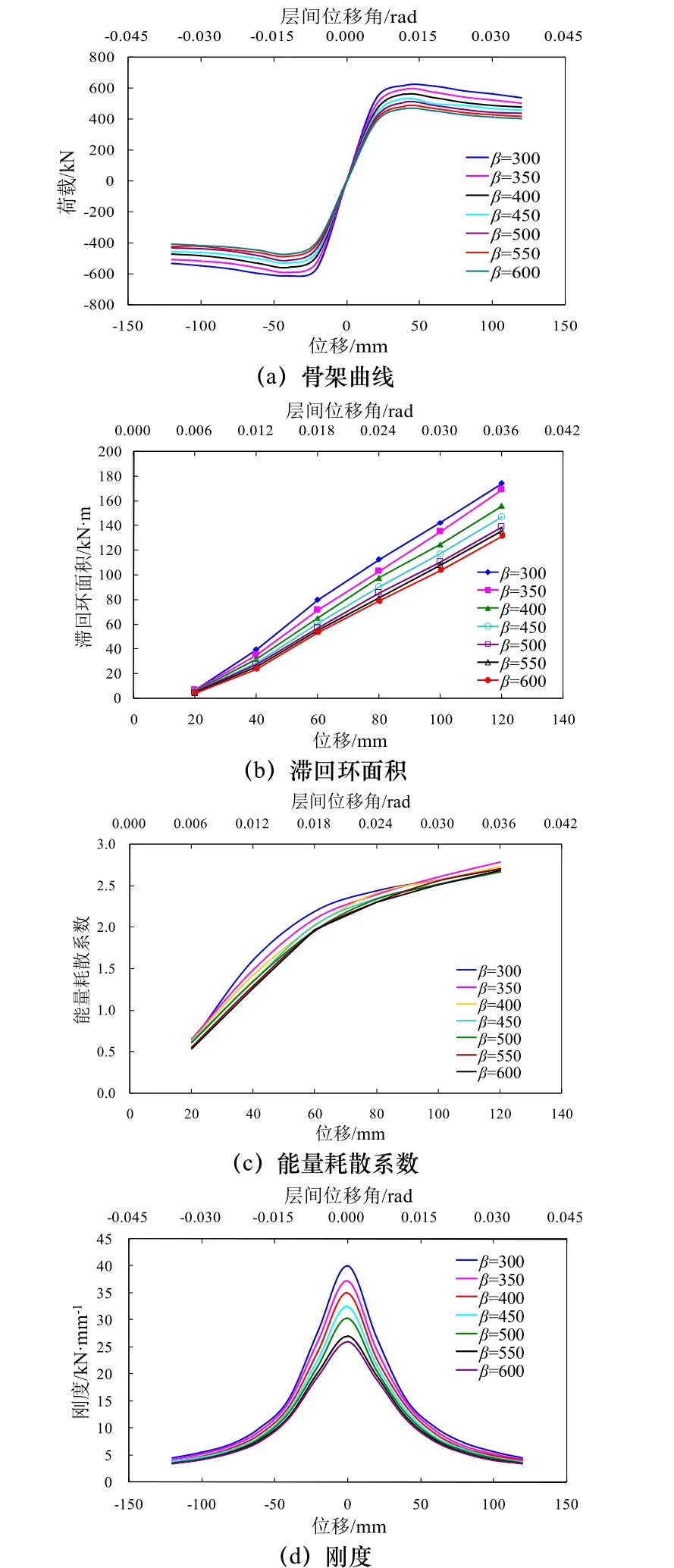
图10 高厚比对滞回性能的影响Fig.10 Influence of height-to-thickness on hysteretic behavior
随着高厚比的增大,单侧开洞钢板剪力墙承载力降低,高厚比β超过500之后,承载力降低幅度很小.当高厚比 β=300时,承载力最大约为 617 kN(正向)和613 kN(负向),当高厚比β=600时,承载力最小约为467 kN(正向)和471 kN(负向).高厚比越大,滞回环面积越小,结构耗能量越少,与骨架曲线类似,高厚比β超过500后,滞回环面积降低幅度很小.层间位移角达到0.027 rad之前,能量耗散系数随着高厚比的增大而减少,高厚比β=500~600的能量耗散系数曲线基本重合.高厚比越大,初始刚度越小,当高厚比从500增大到600时,初始刚度降低幅度较小,说明增大高厚比会显著降低单侧开洞钢板剪力墙的初始刚度.
3.3.4 柱子抗弯刚度η对滞回性能的影响
图 11分别为不同柱子抗弯刚度系数的单侧开洞钢板剪力墙的骨架曲线、滞回环面积曲线、能量耗散系数曲线和刚度曲线.

图11 柱抗弯刚度对滞回性能的影响Fig.11 Influence of column bending stiffness on hysteretic behavior
随着柱子抗弯刚度系数的增大,单侧开洞钢板剪力墙承载力提高.当柱子抗弯刚度系数η从1.0增大到4.0时,承载力逐渐提高但提高幅度逐渐减小;当抗弯刚度系数η从4.0增大到5.0时,承载力提高且幅度突然增大,此时柱子抗弯刚度已接近无限刚的情况.与骨架曲线变化规律类似,抗弯刚度系数越大,滞回环面积越大,结构耗能量越大.除η=4.0和η=5.0两条曲线之外,其他三条能量耗散系数曲线相差不大,基本重合,三条曲线中当η=3.0时能量耗散系数最大.柱子抗弯刚度系数越大,初始刚度越大.当抗弯刚度系数η从1.0增大到3.0时,初始刚度逐渐提高但提高幅度逐渐减小;当抗弯刚度系数η从3.0增大到4.0时,初始刚度提高且提高幅度突然增大,随着层间位移角的增大,两条刚度曲线逐渐重合.

图12 von Mises应力云图Fig.12 von Mises stress diagram
由图12可知,不同抗弯刚度系数的单侧开洞钢板剪力墙拉力带均已充分开展,但钢管混凝土框架柱的应力分布却不尽相同.当η=1.0和η=2.0时,一层钢管混凝土柱大部分屈服,当η超过3.0时,一层钢管混凝土柱仅柱脚部分屈服,且钢管混凝土柱应力分布基本相同.
3.3.5 轴压比n对滞回性能的影响
图 13分别为不同轴压比单侧开洞钢板剪力墙的骨架曲线、滞回环面积曲线、能量耗散系数曲线和刚度曲线.


图13 轴压比对滞回性能的影响Fig.13 Influence of axial compression ratio on hysteretic behavior
随着轴压比的增大,单侧开洞钢板剪力墙承载力降低,但降低幅度不大.当轴压比n=0.4时,承载力最大约为581 kN(正向)和575 kN(负向);当轴压比n=0.8时,承载力最小约为529kN (正向)和520 kN(负向),最小值比最大值降低约9.0%.表明轴压比对单侧开洞钢板剪力墙的侧向承载力影响较小.除轴压比n=0.8外,其他轴压比情况下的滞回环面积曲线重合,表明除轴压比很大时会降低耗能外,当轴压比较小时,轴压比对结构耗能量影响很小.轴压比越大,能量耗散系数越大,耗能效率越高.轴压比越大,初始刚度越小,但初始刚度降低幅度较小,不同轴压比的刚度曲线基本重合,说明轴压比对单侧开洞钢板剪力墙的初始刚度影响较小.
4 结论
(1) 方钢管混凝土柱为钢板墙发挥屈曲后强度提供了有效锚固.在框架柱破坏之前,钢板墙充分屈服并耗散能量,符合“钢板墙先于框架破坏”的抗震设防理念,达到双重抗震设防目标.
(2) 在柱子刚度系数近似相等的条件下,与工字形钢柱相比,采用方钢管混凝土柱作为开洞钢板墙的竖向边框能够显著提高结构承载力、滞回环面积和刚度,但会降低能量耗散系数.柱子抗弯刚度会显著影响单侧开洞钢板剪力墙的承载力、滞回曲线饱满度、能量耗散量和初始刚度,抗弯刚度系数越大,上述指标越大.
(3) 高厚比显著影响单侧开洞钢板剪力墙的承载力、滞回曲线饱满度、能量耗散量和初始刚度,高厚比越大,上述指标越小.当高厚比超过500时,继续增大高厚比,对上述各指标降低幅度不明显.
(4) 轴压比显著影响单侧开洞钢板剪力墙的能量耗散系数,轴压比越大能量耗散系数越大,但对承载力、滞回曲线饱满度和初始刚度影响很小.
References
[1] 陈国栋, 郭彦林, 范珍, 等. 钢板剪力墙低周反复荷载试验研究[J]. 建筑结构学报, 2004, 25(2): 19-26.CHEN Guodong, GUO Yanlin, FAN Zhen, et al. Cyclic test of steel plate shear walls[J]. Journal of Building Structure, 2004, 25(2): 19-26.
[2] 郭彦林, 周明, 董全利, 等. 三类钢板剪力墙结构试验研究[J]. 建筑结构学报, 2011, 32(1): 17-29.GUO Yanlin, ZHOU Ming, DONG Quanli, et al. Experimental study on three types of steel plate shear walls under cyclic loading[J]. Journal of Building Structure,2011, 32(1): 17-29.
[3] PARK Hong-gun, KWACK Jae-hyuk, JEON Sang-woo.Framed steel plate wall behavior under cyclic lateral loading[J]. Journal of Structural Engineering[J]. 2007,133(3): 378-388.
[4] 王先铁, 郝际平, 周观根, 等. 方钢管混凝土柱-钢梁平面框架抗震性能试验研究[J]. 建筑结构学报, 2010,31(8): 8-14.WANG Xiantie, HAO Jiping, ZHOU Guangen, et al.Experimental research on seismic behavior of concrete-filled square steel tube columns and steel beam planar frames[J]. Journal of Building Structure, 2010,31(8): 8-14.
[5] 曹万林, 李刚, 张建伟, 等. 钢管混凝土边框不同高厚比钢板剪力墙抗震性能[J]. 北京工业大学学报, 2010,36(8): 1059-1068.CAO Wanlin, LI Gang, ZHANG Jianwei, et al. Seismic behavior of Steel-plate shear walls with concrete filled steel tube columns and different ratio of height to sectional thickness of the walls[J]. Journal of Beijing University of Technology, 2010, 36(8): 1059-1068.
[6] 李峰, 李慧, 李振敏, 等. 交叉加劲肋钢板剪力墙低周反复荷载试验研究[J]. 西安建筑科技大学学报: 自然科学版, 2009, 41(1): 57-62.LI Feng, LI Hui, LI Zhenmin, et al. Cyclic test of diagonally stiffened steel plate shear wall[J]. Xi’an Univ. of Arch. &Tech.: Natural Science Edition, 2009, 41(1): 57-62.
[7] VIAN D, BRUNEAU M. Special perforated steel plate shear walls with reduced beam section anchor beam I[J].Experimental Investigation, 2009, 135(3): 211-220.
[8] SABOURI-GHOMI S, AHOURIO E, AHOURIO,SAJADI R, et al. Stiffness and strength degradation of steel shear walls having an arbitrarily-located opening[J]. Journal of Constructional Steel Research, 2012, 79(12): 91-100.
[9] 郝际平, 曹春华, 王迎春, 等. 开洞薄钢板剪力墙低周反复荷载试验研究[J]. 地震工程与工程振动, 2009,29(2): 79-85.HAO Jiping, CAO Chunhua, WANG Yingchun, et al.Test on thin steel plate shear wall with opening under cyclic loading[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(2): 79-85.
[10] 聂建国, 朱力, 樊健生, 等. 钢板剪力墙抗震性能试验研究[J]. 建筑结构学报, 2013, 34(1): 61-69.NIE Jianguo, ZHU Li, FAN Jiansheng, et al. Experimental research on seismic behavior of steel plate shear walls[J].Journal of Building Structure, 2013, 34(1): 61-69.
[11] 聂建国, 朱力, 樊健生, 等. 开洞加劲钢板剪力墙的抗侧承载力分析[J]. 建筑结构学报, 2013, 34(7): 79-88.NIE Jianguo, ZHU Li, FAN Jiansheng, et al. Lateral force resistant capacity of stiffened steel plate shear walls with openings[J]. Journal of Building Structure, 2013, 34(7):79-88.
[12] 朱力, 聂建国, 樊健生. 开洞加劲钢板剪力墙的抗侧刚度分析[J]. 工程力学, 2013, 30(9): 200-263.ZHU Li, NIE Jianguo, FAN Jiansheng. Lateral stiffness of steel plate shear walls with openings[J]. Engineering Mechanics, 2013, 30(9): 200-263.
[13] 王先铁, 马尤苏夫, 郝际平, 等. 钢板剪力墙边缘构件的计算方法研究[J]. 工程力学, 2014, 31(8): 175-182.WANG Xiantie, MA Yousufu, HAO Jiping, et al. Calculation methods for boundary elements in steel plate shear walls[J]. Engineering Mechanics, 2014, 31(8): 175-182.
[14] JGJ101-96 建筑抗震试验方法规程[S]. 北京: 中国建筑工业出版社, 1997.JGJ 101-1996 Specification of testing methods for earthquake resistant building[S]. Beijing: China Architecture& Building Press, 1997.
[15] GB 50011-2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50011-2010 Code for seismic design of buildings[S].Beijing: China Architecture & Building Press, 2010.
[16] 韩林海. 钢管混凝土结构—理论与实践[M]. 2版. 北京: 科学出版社, 2007.HAN Linhai. Concrete filled steel tubular structure theory and practice[M]. 2nd ed. Science Press, 2007.
[17] Dassault Systèmes Simulia Corp. ABAQUS Analysis User's Manual Version 6. 10[M]. Providence, RI:Dassault Systèmes Simulia Corp., 2010.
[18] 李海广. 方钢管混凝土框架-单侧开洞薄钢板剪力墙的滞回性能及设计方法研究[D]. 西安: 西安建筑科技大学, 2014.LI Haiguang. Study on hysteretic behavior and design method of concrete-filled square steel tubular frame-thin steel plate shear walls with single side openings[D]. Xi’an:Xi’an University of Architecture & Technology, 2014.
[19] CECS 159: 2004 矩形钢管混凝土结构技术规程[S]. 北京: 中国计划出版社, 2004.CECS 159: 2004 Technical specification for structures with concrete-filled rectangular steel tube members[S].Beijing: China Planning Press, 2004.
[20] ANSI/AISC 341-10. Seismic provisions for structural steel buildings[S]. Chicago, U. S. A.: American Institute of Steel Construction, 2010.
