建筑钢试件拉伸应力与其磁记忆效应漏磁场梯度的对应关系研究

王 威，易术春，苏三庆，兰 艳

（西安建筑科技大学土木工程学院，西安 710055）

无损检测是在不损伤被测对象内部结构和实用性能的情况下，应用多种物理原理和化学现象，对各种工程材料、零部件和结构件进行有效的检验和测试，从而评估被测对象的完整性和安全性．然而，常规的磁无损检测技术只能检测出已经成形的宏观缺陷，无法对早期的隐性损伤进行检测[1-3]．且常规的磁无损检测技术是以外加的强磁场为激励源，将被测对象磁化到磁饱和状态，在实际工程应用中具有一定的局限性．金属磁记忆检测技术是一项新兴的无损检测方法，以地磁场为激励源，测量的是应力引起的残余磁场，能够对铁磁材料的应力集中、早期损伤及损伤程度等进行诊断，防止构件的突发性失效，是迄今为止对铁磁构件进行早期诊断唯一行之有效的无损检测新方法[4-5]．且由于其操作简单、方便和不需要对被测构件进行清理、人工磁化以及贴附传感器等，被广泛应用于石油、化工和机械等领域．

自金属磁记忆检测技术被提出以来，便受到各国学者的普遍重视．Yamamoto等[6]观测了铁磁构件在弱磁场和应力共同作用下磁畴组织的变化；黄松岭等[7]检测了在地磁场的作用下ASTM1020钢板磁信号的变化，研究了磁记忆检测中地磁场的作用；任吉林等[8]对40Cr钢进行高周疲劳试验，研究了疲劳损伤及应力集中对法向漏磁信号的影响规律，并将李萨如图引入磁记忆检测中．然而，磁记忆检测在建筑钢结构中的应用却少有研究，加之建筑钢构件的材性、受力方式及工作环境与上述设备明显不同，故不能将其他领域现有磁记忆理论直接应用于建筑钢结构中[9]．本文通过对钢结构中常用的 Q345B光滑试件和人工预制浅槽试件进行静载拉伸试验，采集规定路径上的法向漏磁场值，研究了不同应力状态下磁记忆信号的变化规律，建立了磁信号特征参量与应力之间的量化关系，为磁记忆检测技术在钢结构领域中的应用打下基础．

1 试验概况

1.1 试验设计

试验材料选用钢结构中广泛应用的 Q345B结构钢，其力学性能指标规定值如表1所示．

为更好的观测应力集中区磁记忆信号的变化特征，本文采用的拉伸试件为光滑试件和人工预制浅槽缺口试件．试件利用线切割机进行加工，同时，为了保证试件的断裂位置位于检测范围内，将中央的检测区域面积适当减小，以增大此区域内的应力．为符合工程实际情况，试件未进行去应力退火处理．实验前在试件的正面测试范围内画好检测线，检测线长度为100 mm．试件的具体尺寸如图1所示．

表1 Q345钢试件力学性能Tab.1 Mechanical properties of Q345 steel specimen

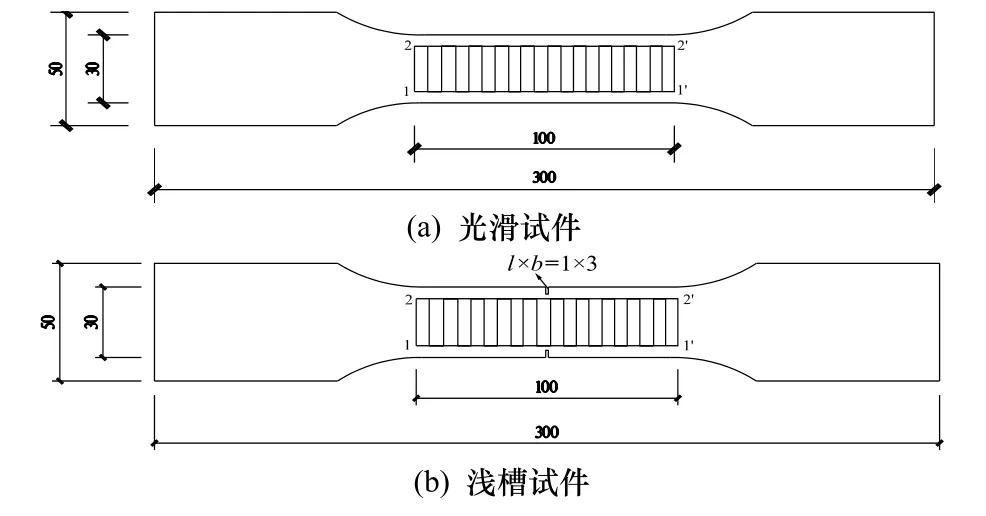
图1 试件尺寸及检测线位置Fig.1 Size of specimen and arrangement of measured lines

1.2 试验设备及方法

拉伸试验在WAW-2000D电液伺服万能试验机上进行，其主要技术参数：最大试验力为2 000 kN，试验力示值相对误差≤±1%．磁记忆信号检测设备选用高精度的WT10B型数字高斯计，其主要技术参数：量程范围：0～200 mT，基本误差：± 2%，分辨率：0.01 mT．

试验开始前，分别对光滑试件和浅槽试件进行轴向拉伸，发现光滑试件和浅槽试件分别加载到96 kN和85 kN时发生屈服，加载到120 kN和110 kN时出现明显的颈缩现象．为了更好地观察试件从弹性阶段过渡到塑性阶段过程中磁记忆信号的变化特征，采取分级加载的方式，并在屈服强度处进行细化．光滑试件的加载等级为：0、40、70、80、90、96、100、110、120 kN；浅槽试件的加载等级为：0、20、40、60、80、85、90、100、110 kN．当载荷达到预先设定值时，采用WT10B数字高斯计进行在线检测．检测时，沿着检测线从左至右逐点依次检测，探头垂直并紧贴于试件表面．

1.3 试验数据优化

加载完成后，对试验数据进行整理，发现每组试件都具有较好的一致性，特别是同一试件中，两条测量线上的漏磁场值基本相同，为减小检测误差，同一试件的检测结果取两条检测线上检测数据的平均值．由于加载装置的夹具也属于铁磁材料，会对试件端头的磁场产生影响，因此，在进行数据分析时，去除试件两端各两个检测点的数据．

2 试验结果及分析

2.1 不同应力对磁记忆信号的影响

试件加载之前，在线测量试件表面的初始漏磁信号，测量结果如图2所示．由图2可知，由于试件未进行去应力退火处理，且加工过程中产生了残余应力．初始时就有较大的磁信号，且曲线均有较大的波动，法向分量过零点的位置与试件的断裂位置不相符，即初始磁信号不能对试件的应力集中进行判断．

图2 初始阶段法向分量磁场强度值Fig.2 Normal component of magnetic field intensity values in initial stage

图3 弹性阶段法向分量磁场强度值Fig.3 Normal component of magnetic field intensity values in elastic stage

图4 塑性阶段法向分量磁场强度值Fig.4 Normal component of magnetic field intensity values in plastic stage

图3为弹性阶段，试件表面磁场强度的法向分量分布曲线．由图3可知，试件表面的磁信号与初始磁信号有很大差异，磁信号曲线出现过零点现象，并沿加载方向近似为一条斜直线且保持稳定，并随着载荷的增加，磁信号法向分量逐渐增大．这是由于应力的存在使得磁弹性能逐渐增大，为了使试件总的自由能趋于最小，在试件内部的位错聚集处，磁畴必将发生运动，弹性应力的存在能有效促进磁畴沿着最大拉应力方向取向，从而增大了试件的空间漏磁场[10]．

图4为塑性阶段，试件表面磁场强度的法向分量分布曲线．由图4可知，磁场分布曲线在试件的最终断裂处附近出现小幅波动现象，表现出一定的非线性变化．这是由于塑性阶段，试件内部的磁场组织的变向和分隔作用，使得试件表面漏磁场发生了畸变，进而表现出一定的非线性变化．这与Doubov所提出的应力集中区磁场法向分量具有“峰-峰值”的现象，具有一定的偏差．

为研究磁场法向分量过零点的位置与试件最终断裂位置是否存在偏差，分别对光滑试件和浅槽试件过零点的位置进行统计，如表2所示．零点不在检测点上时，采用线性内插的方法确定其位置．光滑试件和浅槽试件的最终实际断裂位置分别在30和40 mm处．

由表2可知，光滑试件磁场法向分量零点位置在不同应力下并不唯一，出现了“漂移”现象，表现为随着应力的增大，零点位置逐渐向试件的最终断裂位置移动，并在400 MPa时已基本位于断裂位置处．对于浅槽试件，由于浅槽缺陷的存在，试件中部有很大的应力集中，在不同应力下浅槽试件磁场法向分量零点位置唯一，且均出现在试件中部，与试件最终断裂位置一致．因此，Doubov所提出的应力集中区磁场法向分量过零点的现象，对于光滑试件，虽不能准确的判断应力集中区，但仍具有一定的指导意义；对于浅槽试件具有很好的一致性，能准确的判断出应力集中区．

表2 光滑试件和浅槽试件不同应力下磁场零点位置Tab.2 Zero position of magnetic field under different tensile loads of smooth specimen and slotted specimen

2.2 不同应力对磁记忆信号梯度值的影响

从磁偶极子模型可知，磁信号反映的是应力集中区的自由漏磁场的积分场．对磁信号进行微分，可以有效的排除外界恒定磁场对试验结果的干扰．本文采用基于离散数据的中心差分算法对磁信号法向分量进行一阶微分

式中： Ki为第i个检测点的磁场法向分量梯度值；分别为第i个检测点的磁场法向分量值和位置坐标．

图5和图6分别给出了弹性阶段和塑性阶段，试件表面磁信号法向分量梯度值的分布曲线．在弹性阶段，磁场梯度值随应力的增大而缓慢增大，光滑试件由于应力集中不明显，曲线的波动整体较小；浅槽试件由于中部具有较大的应力集中区，曲线的波动整体较大，并在应力集中部位出现“峰值”．在塑性阶段，磁场梯度值随应力的增大而快速增大，光滑试件和浅槽试件均在应力集中部位(最终断裂处)出现“峰值”．

图5 弹性阶段法向分量磁场梯度值Fig.5 Normal component of magnetic field gradient values in elastic stage

图6 塑性阶段法向分量磁场梯度值Fig.6 Normal component of magnetic field gradient values in plastic stage

为研究磁场法向分量梯度最大值位置与试件最终断裂位置是否存在偏差，分别对光滑试件和浅槽试件梯度最大值位置进行统计，如表3所示．

表3 光滑试件和浅槽试件不同应力下梯度最大值位置Tab. 3 Position of maximum gradient under different tensile loads of smooth specimen and slotted specimen

由表3可知，只有在应力为133.3 MPa时，梯度最大值位于20.0 mm处，其他应力下，梯度最大值均位于30.0 mm处，即试件的最终断裂处，可能是由于试件加载初期，应力集中程度较小，且夹具对试件端部产生了一定的影响．因此，光滑试件梯度最大值位置较过零点位置能更好的判断应力集中部位．对于浅槽试件，梯度最大值位置均在40.0 mm处，因此，对于已存在的应力集中区，梯度最大值位置和过零点位置都能准确判断应力集中部位．

通过对磁信号试验数据的分析，提取磁场梯度算术平均值对应力的导数作为特征参量，并建立K′与应力σ的关系曲线，如图 7所示．其中 Kmean值由式(2)确定．

式中：n为检测线上的检测点数，即n=17．

由图7可知，在弹性范围内，导数K′随着应力σ的增加而增大；当应力增加至屈服强度时，K′值出现最大值，其中光滑试件达到6.92×10-5，浅槽试件达到5.08×10-5，较初始阶段分别增大了7.8倍和10.3倍；屈服以后，K′值随应力σ增加逐渐减小．因此，可以提取特征参量K′，对试件是否进入塑性阶段进行判定，且浅槽试件由于应力集中程度更大，对K′值的变化更加敏感．

图7 应力σ与导数K′之间的曲线Fig.7 The relation curve of stress σ and derivative value K′

图8 应力σ与梯度之间的曲线Fig.8 The relation curve of stress σ and gradient

为更好的反映试件应力集中程度，建立磁场梯度最大值的绝对值Kmax与应力σ的关系曲线，如图8所示．在弹性阶段，随着试件内部应力的增加，磁场梯度值缓慢增大；进入塑性阶段后，磁场梯度值急剧增大，当试件出现明显的颈缩现象时，其中光滑试件达到0.033，浅槽试件达到0.042，较初始阶段分别增大了4.1倍和4.2倍．这是由于随着载荷的增加，试件内部应力水平增大，在应力集中部位由于磁机械效应的作用使得材料表面漏磁场增强而导致的．采用指数增长拟合函数式(3)对上述数据进行非线性拟合

光滑曲线：A=3.99×10-5，R0=0.0163，K0=0.0068，拟合度为 95.3%；缺陷试件：A=5.197×10-5，R0=0.014，K0=0.0105，拟合度为98.3%．结果表明，浅槽试件由于应力集中程度更大，对值的变化更加敏感，且值可以用来表征试件的受力状态，评估损伤程度，并能通过其量化关系反演材料的应力状态．

3 结论

(1) Doubov所提出的应力集中区磁场法向分量过零点和梯度最大值，能较好的判断应力集中位置；但应力集中区磁场法向分量出现“峰-峰值”，对于光滑和浅槽试件，均具有一定的偏差，不能作为早期损伤判断的依据．

(2) 分析了磁场梯度特征参量K′随应力σ的变化特征，发现当试件达到屈服极限时，K′出现最大值，可以提取K′值作为特征量，对试件是否进入塑性阶段进行判定．

(3) 建立了磁场梯度最大值的绝对值与应力σ的量化关系，可以利用来表征试件的受力状态，并能通过其量化关系反演材料的应力状态，评估损伤程度．

References

[1] YANG L J, LIU B, CHEN L J, et al. The quantitative interpretation by measurement using the magnetic memory method(MMM)-based on density functional theory[J].NDT&E International, 2013, 55: 15-20.

[2] 王威, 樊浩, 苏三庆, 等. 钢结构对接焊缝隐性损伤的磁记忆检测试验研究[J]. 西安建筑科技大学学报: 自然科学版, 2014, 46(4): 497-501.WANG Wei, FAN Hao, SU Sanqing, et al. Experimental detection on implicit damage of butt weld of steel structure by magnetic memory testing[J]. J. Xi’an Univ. of Arch. &Tech: Natural Science Edition, 2014, 46(4): 497-501.

[3] 王威, 樊浩, 杨为胜, 等. 钢结构隐性损伤的磁记忆识别机理及试验研究[J]. 结构工程师, 2014, 30(5): 139-145.WANG Wei, FAN Hao, YANG Weisheng, et al. Identification mechanism and experiment of metal magnetic memory in steel structure implicit damage testing[J].Structural Engineers, 2014, 30(5): 139-145.

[4] 刘静. 建筑钢结构的磁记忆感应机理及信号采集处理方法研究[D]. 西安: 西安建筑科技大学, 2014.LIU Jing. The research on mechanism of steel structure building using magnetic memory testing and the method of magnetic signal acquisition-processing[D]. Xi’an:Xi’an Univ. of Arch. & Tech, 2014.

[5] 杨为胜. 磁记忆检测建筑钢结构损伤的量化评判方法研究[D]. 西安: 西安建筑科技大学, 2014.YANG Weisheng. Research quantification evaluation method for damage of steel structure building based on metal magnetic memory testing[D]. Xi’an: Xi’an Univ. of Arch. & Tech, 2014.

[6] YAMAMOTO K, SASAKI T, YAMASHIRO Y. Magnetization change due to stress change in a constant magnetic field on amorphous ribbons[J]. Journal of Applied Physics, 1997, 81(8): 5796-5798.

[7] 黄松岭, 李路明, 施克仁, 等. 地磁场激励下残余应力分布的磁检测方法[J]. 清华大学学报: 自然科学版,2002, 42(11): 1426-1428.HUANG Songling, LI Luming, SHI Keren, et al. Magnetic testing method of residual stress distribution by geomagnetic excitation[J]. J Tsinghua Univ.: Science and Technology, 2002, 42(11): 1426-1428.

[8] 任吉林, 陈曦, 罗声彩, 等. 高周疲劳损伤的磁记忆二维检测研究[J]. 航空学报, 2012, 33(6): 1147-1155.REN Jilin, CHEN Xi, LUO Shengcai, et al. Research of high-cycle fatigue damage by two-dimensional magnetic memory testing[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(6): 1147-1155.

[9] 樊浩. 建筑钢结构磁记忆检测仪的关键技术研究[D].西安: 西安建筑科技大学, 2014.FAN Hao. Research on the key technology of magnetic memory inspection instrument for steel structure building[D]. Xi’an: Xi’an Univ. of Arch. & Tech, 2014.

[10] 任吉林, 林俊明, 池永滨, 等. 金属磁记忆检测技术[M]. 北京: 中国电力出版社, 2000.REN Jilin, LIN Junming, CHI Yongbin, et al. Metal magnetic memory testing technology[M]. Beijing: China Electric Power Press, 2000.