矩形钢管混凝土框架的拟静力试验研究

李 斌，杨晓云，高春彦,3

（1.内蒙古科技大学建筑与土木工程学院，内蒙古 包头 014010;2.内蒙古黄岗矿业有限责任公司，内蒙古 赤峰025350;3.南京航空航天大学航空宇航学院，江苏 南京210016）

随着钢管混凝土结构在建筑领域的广泛应用，钢管混凝土框架结构体系越来越多地应用到高层及超高层等复杂结构体系中，结构形式主要由钢管混凝土柱与钢梁(或钢-混凝土组合梁) 组成，典型工程主要有杭州瑞丰国际商务大厦、深圳赛格广场大厦、台北101大厦等[1]．台北101大厦设计时，考虑到强烈的台风以及地震作用等不利因素，地上主楼结构由巨柱、核心筒与外伸桁架梁等构件组成，在主楼四周每侧分别采用两根矩形钢管混凝土柱，最大尺寸达到3 m×2.4 m×80 mm，自地下5楼贯通至地上 90楼，柱内灌入自填充高性能混凝土[2]．目前，国内外学者主要有 Matsui[3]、Kawaguchi[4]、王文达[5]、王来[6]、Herrera[7]、张文福[8]等对由钢管混凝土柱-钢梁组成的框架进行了一系列静、动力试验研究和理论分析，这些研究成果为钢管混凝土框架在实际工程中的应用提供了试验依据和技术支持．

众所周知，钢管混凝土用作受压构件时，可以充分发挥钢管和混凝土两种材料协同工作的优势，使得承载能力提高，塑性增加，施工方便，取得经济的效果．但当其用作梁式构件时，钢管对核心混凝土的约束效果并不明显．文献[9]研究表明，矩形钢管混凝土梁式构件屈服后，抗弯承载力并没有下降，试件表现出良好的延性和后期承载力，这对于结构抗震非常有利．基于上述研究成果，本文对一榀单跨三层全矩形钢管混凝土框架模型进行了拟静力试验研究，分析了该类框架体系的破坏机理和破坏特征、承载能力、滞回曲线、延性、强度与刚度退化、耗能能力等．

1 试验研究

1.1 模型设计

本次试验以一栋10层矩形钢管混凝土框架结构办公楼为背景，试验试件为一榀单跨三层矩形钢管混凝土框架，由矩形钢管混凝土梁和方钢管混凝土柱组成[10]．试件采用1:4比例缩尺制作，试件模型尺寸如图1所示，柱脚详图如图2所示，框架模型梁柱节点采用外加强环连接形式如图3所示．试件参数见表1．

图1 框架模型尺寸Fig.1 Frame model

图3 节点详图Fig.3 The detail view of joint

图2 柱脚详图Fig.2 The detail view of column foot

表1 框架试件尺寸和参数Tab.1 Sizes and parameters of specimens

框架试件钢管内灌注C40混凝土，混凝土中掺入聚羧酸减水剂，以增强其流动性．由于钢管柱较长且内径较小，采用手工逐段浇筑法，混凝土自钢管上口灌入的同时利用振捣器在钢管外部振捣．在柱脚和每层钢管上都留有5 mm的排气孔，保证管内混凝土的浇筑质量．矩形钢管混凝土梁顶板由三块钢板拼焊而成，先焊接两端钢板，中间预留混凝土浇筑孔，长度为650 mm，待梁混凝土浇筑和自然养护完毕，将浇筑孔处混凝土磨平后焊接中间盖板．在梁两端侧板处留有 5mm的排气孔，保证混凝土浇筑密实．排气孔直径较小且位于受力影响较小处，分层分段进行浇筑．梁柱节点采用外加强环连接形式，利用外加强环板传递梁端弯矩，利用竖向焊缝传递梁端剪力．

试验用钢材均采用Q235钢，钢管内填充C40混凝土，其配合比为，水泥∶水∶砂子∶石子∶粉煤灰∶膨胀剂∶聚羧酸减水剂=1∶0.46∶2.15∶2.92∶0.27∶0.09∶0.01．钢材和混凝土的力学性能指标见表2．

表2 材料力学性能指标（MPa）Tab.2 Mechanics properties of materials

1.2 试验加载装置及加载制度

本次试验采用拟静力加载，加载装置如图4所示．柱顶竖向荷载分别由两个2 000 kN液压千斤顶施加．千斤顶上端设置滑动滚轴，保证试件竖向受压时，发生同步水平移动．顶层梁端设置厚度为40 mm的加载端板，与反力墙上的MTS液压伺服作动器连接，水平侧向力或位移施加在顶层梁轴线处．为保证框架柱下端嵌固，设计了500 mm高的钢筋混凝土基础梁，用三对地脚螺栓将其固定，使其在试验过程中不发生移动或转动．

由于本次试验框架平面外计算高度较大，按照文献[11]进行了平面外稳定性验算，满足要求．为了更好地保证试验框架在加载过程中不发生平面外失稳，在各层梁两侧分别安装了水平侧向保护装置．该装置设有两个轴承，安装时轴承不与梁侧面完全接触，留有3～5 mm间隙，若试验过程中发生平面外失稳时，梁会与轴承接触，轴承可沿着梁侧板自由滑动．

试验开始时，首先将柱顶竖向荷载施加到预定值后保持恒定不变，然后按照加载制度在梁端施加水平往复荷载．水平荷载根据文献[12]采用荷载-位移混合控制加载．试验前估算的结构屈服荷载为70 kN，在荷载控制阶段，荷载增量为10 kN，每级循环一周，直至结构屈服．试件屈服后，以屈服位移的倍数为级差控制加载，每级循环一周；当达到极限荷载时，位移控制每级循环三周，直至结构变形过大，承载力降至极限荷载的65%，停止加载．

图4 试验加载装置Fig.4 Test setup

1.3 试验量测内容和测点布置

本次试验的框架梁柱采用外加强环节点，加强环处刚度较大，对梁端起加强作用，梁端塑性铰应产生在加强环板之外．在梁端截面处 40～120 mm范围内，每间隔40 mm粘贴一排应变片，共三排，监测塑性铰的位置和长度．梁端表面应变片位置如图5所示．

图5 框架梁应变片布置Fig.5 Strain gague layout of frame beam

框架的柱脚四周均设置加劲肋，加劲肋处刚度较大，不会产生塑性铰，框架柱脚塑性铰应产生在加劲肋板以上，应变片位置如图6所示（柱脚近端指离水平荷载加载端较近的一端，远端反之）．在梁柱节点处，梁比柱的总抗弯承载力要小很多，塑性铰不会在节点处的框架柱出现，所以布置少量应变片进行监测．

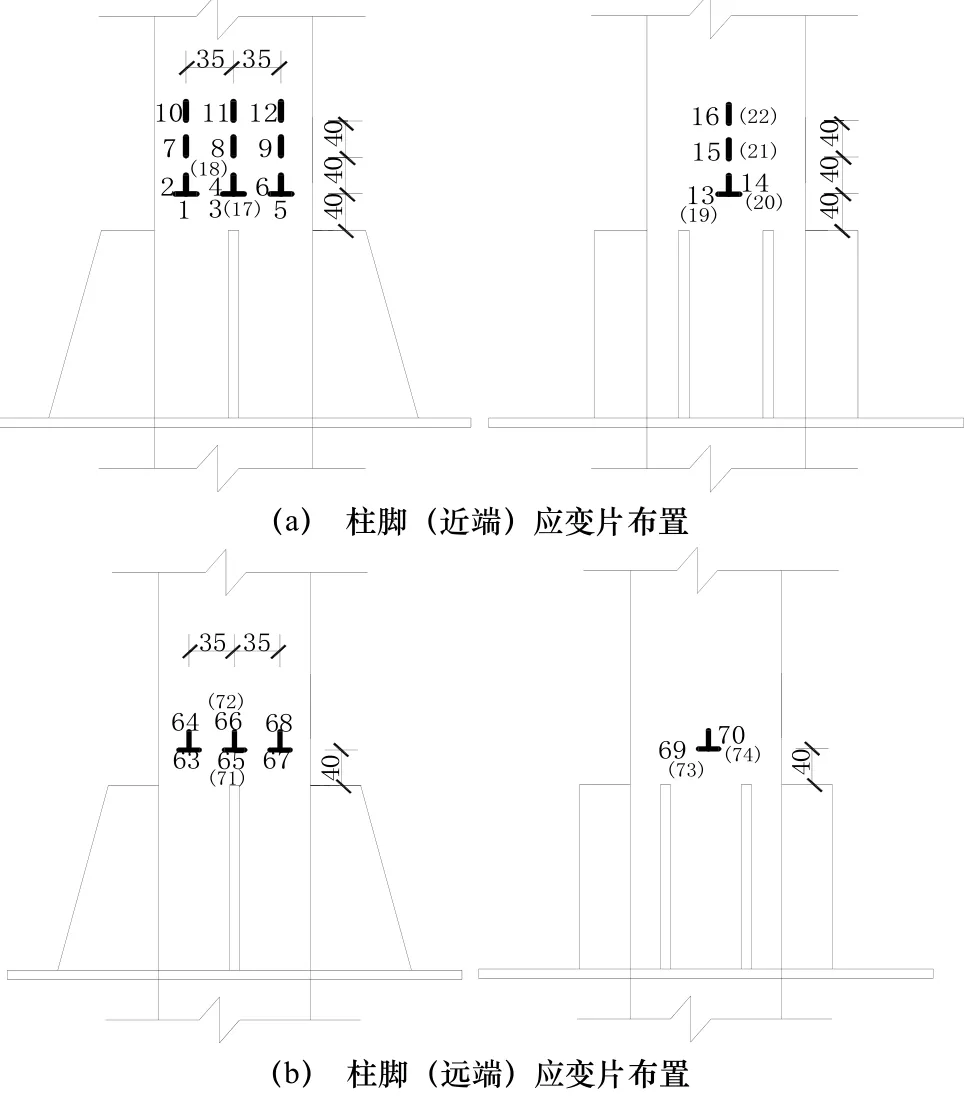
图6 框架柱应变片布置Fig.6 Strain gague layout of frame column

2 试验结果分析

2.1 破坏特征分析

试件呈“强柱弱梁”破坏机制．加载初期，水平荷载较小时，框架试件处于弹性工作状态．当水平荷载（位移）增加到一定数值时，二层近载侧距离加强环板40 mm处的梁端首先达到屈服，反向加载时，远载侧二层梁端也屈服；继续加载，加强环板外二层梁端截面的顶板、底板、侧板鼓曲程度加重，焊缝撕裂，内部混凝土有被压碎的声响，如图7（a）、（b）、（c）所示；此时一层近载侧梁端、反向加载时远载侧梁端相继出现顶板、底板鼓曲、与侧板的焊缝撕裂现象；试验结束前，三层加强环板外的梁端也达到了屈服并出现钢板及焊缝撕裂，靠近加载端的柱脚在加劲肋板以上40～100 mm范围内出现了轻微鼓曲现象．由试验现象和试验结果可以看出，由于采用外加强环节点，加强环板的存在使节点区域强度和刚度均较大，在节点形成了刚域，因此本文矩形钢管混凝土框架模型结构的梁端塑性铰形成于距加强环板外约40 mm的控制截面处，即梁的h/3（h为梁高）处；柱脚在加劲肋之上40～100 mm范围内轻微鼓曲．

图7 破坏形态Fig.7 Failure modes

2.2 破坏机制

在塑性铰形成过程中，正向加载时二层框架梁首先形成塑性铰1，塑性铰2晚于铰1形成，底层梁塑性铰3先于铰4出现，顶层梁塑性铰5先于铰6出现，如图8所示．整个试验加载过程中，塑性铰先出现在框架各层梁端，最后是柱脚，且柱脚的塑性铰是在所有梁端都出塑性铰后才形成，充分说明试件属于梁铰破坏机制，符合“强柱弱梁”的设计原则，柱脚塑性铰的出现宣告试件破坏．

图8 框架塑性铰出现顺序Fig.8 The order of plastic hinges

2.3 滞回曲线

滞回曲线是结构在循环荷载下受力与变形关系的反映，是结构抗震性能的宏观表现．试验获得的水平荷载—顶层梁端位移P-Δ滞回曲线如图9所示．由图可知：本次试验框架试件的滞回曲线呈现饱满的梭形，直至试验结束也没有出现捏缩现象，说明具有良好的抗震性能和耗能能力．屈服之前试件的变形较小，斜率基本保持不变，卸载后残余变形较小．屈服后试件变形增长的速率大于荷载的增长速率，强度和刚度退化缓慢；正向加载时实测的平均强度降低系数是0.969，相对刚度P/Δ下降值为3.86%；反向加载时实测的平均强度降低系数是0.955，相对刚度P/Δ下降值为9.33%．超过极限荷载后，试件的承载能力下降．

由文献[13]可知，结构在循环荷载下性能的退化特征及规律主要取决于所采用的建筑材料．本次试验框架试件的滞回曲线没有出现与钢筋混凝土框架类似的捏缩现象，主要是由于在加载过程中，钢管对核心混凝土的紧箍作用使得混凝土的强度提高，塑性性能改善，而混凝土的存在延缓了钢管发生局部屈曲，两者的协同工作使得塑性铰依次出现在各层梁端、柱脚，最后结构形成机构而破坏．可知该类框架在循环荷载下的地震反应类似于钢框架，可以应用于工程实践中．

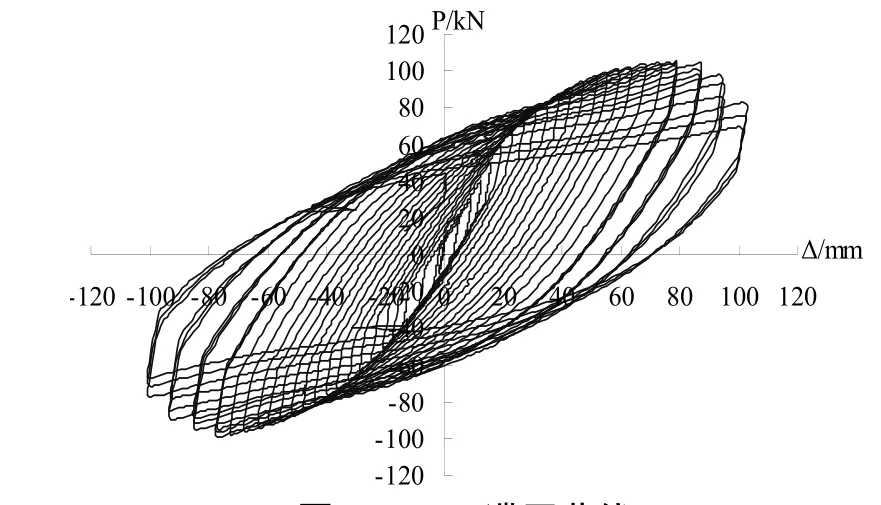
图9 P-Δ滞回曲线Fig.9 P-Δ hysteretic curve

图10 P-Δ骨架曲线Fig.10 P-Δ skeleton curve

2.4 骨架曲线和延性分析

将试件滞回曲线每次循环的峰值点连接起来形成的曲线，称为骨架曲线．由骨架曲线可以直观反映出结构的承载力、变形等性能，可进一步定量评价结构的延性．图10骨架曲线中已标明各特征点．由图可知，在荷载控制阶段，当加载到±50kN以前，框架刚度基本保持不变，但已有一定的塑性发展．当加载到±60kN时，骨架曲线稍有偏转，刚度略有降低，预示框架将进入弹塑性阶段．当框架顶层的水平荷载增加到±74kN时，框架二层和一层梁端应变先后超过屈服应变，试件P-Δ骨架曲线的斜率在A点明显减小，表明框架在该点进入屈服阶段，将A点纵坐标值定为Py．

当位移为1.5Δy时，三层梁端应变值均大于屈服应变，说明框架梁端全部达到屈服．当位移为2.5Δy时，P-Δ骨架曲线达到最大荷载点B，B点对应的荷载为框架承受的极限荷载Pm=105.9kN，此时柱脚应变已达到甚至超过屈服应变，说明柱脚也达到屈服；水平位移达到－2.5Δy时，P-Δ骨架曲线达到反向最荷载点B＇，相对应的反向极限荷载Pm＇=－99.5kN．

试件超过极限荷载以后，变形随着荷载的增加继续增长，荷载呈现缓慢下降趋势．当顶层水平位移达到 3.25Δy时，第一循环时荷载降至破坏点 C，荷载值为Pu= 0.85Pm= 93 kN，该值高于屈服荷载（即Pu＞Py）．此时延性系数μ=3.11；当顶层水平位移达到－3.25Δy时，第一循环时框架达到反向破坏点C＇，此时Pu＇=－84.9kN，延性系数μ＇=3.08．至此框架试件已经破坏，加载到3.25Δy第三循环时试验停止．

从骨架曲线图可以看出，试验框架屈服后仍有一定的强度上升段，达到峰值荷载后结构承载力下降段的斜率不大，表明结构的强度退化不显著．试件正、反向位移延性系数均大于 3，说明具有良好的整体变形能力．

2.5 层间位移与转角

表3 层间位移和转角Tab. 3 Story displacement and angle

试验框架各层在屈服、极限和破坏时的层间位 移转角δ/h（即各层层间位移δ与层高h的比值）见表3．由表3可知，试验框架破坏时各层的极限层间变形能力都远大于1 /50，说明该类框架具有良好的变形能力，完全满足现行《建筑抗震设计规范》（GB50011-2010）对框架结构在罕遇地震作用下的弹塑性层间变形要求．

2.6 强度与刚度退化

本次试验用总体强度退化系数λj来衡量试验框架的强度退化情况．总体强度退化系数 λj定义为，在结构屈服之后的位移加载阶段，第j次加载的各循环峰值荷载的平均值 Pj与极限荷载 Pmax的比值．试验框架的总体强度退化曲线如图11所示．由图可知，框架模型刚达到屈服时总体强度退化现象并不明显；但在位移控制阶段后期，超过极限荷载之后，强度退化比较明显，原因在于此时框架梁端已全部形成塑性铰，钢板鼔曲严重甚至被撕裂，核心混凝土被压碎挤出，柱脚也达到屈服并发生了较大变形，此时钢管和混凝土的协同工作能力下降引起的．反向加载时框架试件的总体强度退化速率基本与正向加载时相同．

图11 总体强度退化曲线Fig.11 Overall strength degradation curve

图12 整体刚度退化曲线Fig.12 Overall stiffness degradation curve

在循环加载过程中，结构的刚度逐渐下降，主要体现在从框架整体屈服到峰值荷载前弹塑性上升段、达到峰值荷载后下降段的刚度退化．以结构屈服后位移加载阶段的割线刚度来反映框架的整体刚度退化，框架各层割线刚度与Δ/Δy的关系如图12所示．由图可知，框架各层的整体刚度退化均呈退化趋势，主要是由于框架屈服后，梁端和柱端塑性铰区段的钢管内混凝土逐渐开裂，甚至被压碎，损伤较为严重，钢材塑性的发展以及焊缝开裂引起的．

2.7 结构耗能

在循环反复荷载加载过程中，加载时框架吸收能量，卸载时框架放出能量，结构在一个循环中吸收的能量减去放出的能量就是结构耗散的能量．弹性阶段，没有产生残余应变，框架结构通过刚体震动释放地震能量；进入塑性阶段，通过滞回环耗散能量．本文采用等效粘滞阻尼系数he来评价框架的耗能能力，在各位移加载阶段的等效粘滞阻尼系数he见表4．

表4 试件的耗能指标Tab.4 Energy dissipation index of specimen

由表4可知：框架结构在屈服初期he值很小，说明此时结构出现塑性铰的部位少，塑性铰转动能力仍不充分，结构耗散的地震能量较少；随着梁端水平位移的增加，框架结构的滞回环越来越饱满，对应的he也逐渐增大，一方面是由于越来越多的框架梁端出现塑性铰，塑性铰不断出现和转动；另一方面由于钢管内混凝土的裂缝发展、钢管塑性的发展以及两种材料间的内摩擦等，使得框架结构吸收的能量越来越多．当施加到破环荷载时，he值最大，此时框架结构梁端塑性铰的发展已十分充分，当柱脚塑性铰出现时，结构形成机构而破坏．

3 结论

(1)矩形钢管混凝土框架呈“强柱弱梁”破坏机制，试件破坏时加强环板外三层梁端和一层柱脚全部出现塑性铰，梁的顶板和底板严重鼔曲，顶板与侧板的焊缝撕裂，柱脚轻微鼔曲．

(2)矩形钢管混凝土框架的滞回曲线饱满，捏缩现象不明显，表现出良好的抗震性能和耗能能力．破坏时位移延性系数均大于 3，各层层间位移角均大于1/50，满足罕遇地震作用下层间弹塑性变形要求．

(3)试验框架的整体强度、刚度退化现象并不明显，试件整体屈服后等效阻尼系数he呈增加趋势，破坏时he达到了0.441，说明框架耗能性能良好，可以应用于实际工程中．

References

[1] 韩林海.钢管混凝土结构理论与实践(第二版) [M]. 北京:科技出版社,2007.HAN Linhai. Theory and practice of concrete-filled steel tubular structure [M]. Beijing: Science Press, 2007.

[2] 谢绍松, 张敬昌, 钟俊宏. 世界第一楼—台北101大楼之结构设计[J]. 建筑施工.2005,27(10):1-4.XIE Shaosong, ZHANG Jingchang, Zhong Junhong.World's No.1 Skyscraper—Structural Design for Taipei 101[J].Building Construction. 2005,27(10):1-4.

[3] Matsui C. Strength and behavior of frames with concrete filled square steel tubular columns under earthquake loading. Proceeding of 1st international specialty conference on CFST. Harbin, 1985:143-146.

[4] Kawaguchi J, Morino S, Sugimoto T. Elastic-plastic behavior of concrete-filled steel tubular frames. Proceedings of the engineering foundation conference on steel and concrete composite construction Ⅲ, ASCE. New York,USA,1997:272-281.

[5] 王文达, 韩林海, 陶忠.钢管混凝土柱-钢梁平面框架抗震性能的试验研究[J]. 建筑结构学报, 2006, 27(3): 48-58.WANG Wenda, HAN Linhai, TAO Zhong. Experimental research on seismic behavior of concrete filled CHS and SHS columns and steel beam planar frames[J]. Journal of Building Structures.2006,27(3):48-58.

[6] 王来, 王铁成, 陈倩. 低周反复荷载下方钢管混凝土框架抗震性能的试验研究[J]. 地震工程与工程振动.2003, 23(3) : 113- 117.WANG Lai, WANG Tiecheng, CHEN Qian. Experimental study on seismic performance on concrete-filled rectangular tubular frame under low-reversed cyclic loading[J]. Earthquake engineering and engineering vibration.2003, 23(3) : 113-117.

[7] HERRERA, RICLE J M, SAUSE R. Seismic performance evaluation of steel moment resisting frames with concrete filled tubular columns. Proceeding of the international workshop on steel and concrete composite construction. October, Taiwan,2003.

[8] 张文福.单层钢管混凝土框架恢复力特性研究[D].哈尔滨:哈尔滨工业大学, 2000.ZHANG Wenfu. Research on the restoring force characteristics of the monolayer concrete-filled steel tubular frame[D]. Harbin: Harbin institute of technology, 2000.

[9] 蒋涛.薄壁矩形钢管混凝土结构的理论和试验研究[D].上海:同济大学,2003.JIANG Tao. Theoretical and experimental research on concrete filled rectangular thin-wall steel tubular structure [D]. Shanghai: Tongji University, 2003.

[10] 杨晓云.矩形钢管混凝土框架结构的抗震性能研究[D].包头: 内蒙古科技大学, 2014.YANG Xiaoyun. Research on Seismic Behavior of Concrete-filled Rectangular Steel Tubular Frames[D]. Baotou:Inner Mongolia University of Science and Technology, 2014.

[11] CECS159:2004. 矩形钢管混凝土结构技术规程[S]. 北京:中国计划出版社,2004.CECS159:2004. Technical specification for structures with concrete-filled rectangular steel tube members [S].Beijing: Chinese Planning Press, 2004.

[12] JGJ101-96. 建筑抗震试验方法规程[S].北京:中国建筑工业出版社,1997.JGJ101-96.Test methods for earthquake resistant building[S]. Beijing: Chinese Building Industry Press, 1997.

[13] 李磊,郑山锁,王斌, 等.型钢高强混凝土框架的循环退化效应[J].工程力学,2010,27(8):125-132.LI Lei, ZHENG Shansuo, WANG Bin, et al. Cyclic deterioration effect of the steel reinforced high strength concrete frame[J]. Engineering Mechnics, 2010, 27(8): 125-132.