基于ABAQUS的钢筋混凝土收缩徐变分析
2015-01-23张望喜谭泽腾
张望喜,谭泽腾,薛 凯
(湖南大学土木工程学院,湖南 长沙410082)
混凝土的收缩徐变受温度、湿度、配合比、断面形状及尺寸、水泥性质、骨料性质、混凝土养护条件等各种因素的影响,对其进行精确测量非常困难,因为这些因素很多是无法量化的.Z. P. Bazant[1]等对现有的收缩徐变实测结果数据进行汇总,为徐变收缩预测模型的拟合提供了方便.基于弹性徐变理论的按龄期调整的有效模量法在实际工程中应用最为广泛,关于混凝土的徐变计算理论还有继效流动理论、徐变率法、有效模量法、弹性老化理论.
目前混凝土主要的徐变收缩计算模型[2]有CEB-FIP90、GL2000、ACI209、B3、PCA 等.上述模型中除 B3[3]外,其他模型都未能充分考虑大体表比构件湿度扩散的尺度效应.赵昕[4]在对巨型构件的竖向位移及内力重分布进行计算分析时采用B3模型.R.W.Howells[5]等对不同的收缩徐变模型进行了参数的敏感性分析,从研究的结果来看,CEB-FIP、EC2、BP-KX、ACI、B3+、B3等各个国家规范或者学者提出的计算模型受参数的影响很敏感,而CEB-FIP1990能比较真实的预测结构的时变变形.
当前普遍应用的结构分析软件中 MIDAS 和SAP等可以在计算中考虑混凝土徐变收缩效应.MIDAS[6]的徐变收缩模式比较丰富,包括了ACI、CEB-FIP、韩国、日本等建议模式.SAP2000中的徐变收缩模式采用的是 CEB-FIP(1990)计算模式.采用现有软件计算收缩徐变,虽然易于计算,方便工程设计,但对于钢筋效应的考虑不够精确,对于一些复杂的预测模型如BP、B3的实现仍困难重重.软件精度不高且各类软件对于平面单元和水平构件的徐变收缩效应的考虑及计算方法需要进一步完善.
本文通过ABAQUS编制收缩徐变分析子程序,对配筋柱和单层单跨框架在收缩徐变影响下的内力重分布进行研究.
1 徐变系数的拟合
为了减小数据存储量,加快计算速度,需要将现有的徐变系数计算公式拟合成指数函数的形式,相应指数函数 ekix与砼徐变变化规律相似,因此多选用1-ekix作为基函数.当ki<0时,采用不同的ki得到的基函数在区间[0, +∞]上是线性无关的,据此可构建出徐变系数的Dirichlet级数形式:

采用 MATLAB自带的非线性拟合函数LSQCURVEFIT进行四参数的徐变系数的拟合.取m=4,取初始值 λ1=1、λ2=0.1、λ3=0.01、λ4=0.001,不断改变 λj值,使的值近似等于终极徐变值.本节对湿度为 80%,构件截面尺寸为 250 mm×250 mm的C30混凝土柱采用CEB-FIB1990模型得到的徐变数据拟合出徐变曲线.为了更好地模拟混凝土徐变的长期效应,拟合对应7 d、14 d、28 d、60 d、90 d、180 d、365 d、600 d、1 000 d、3 000 d的徐变系数,徐变最终值对应6 000 d的徐变值.拟合结果如图1所示.
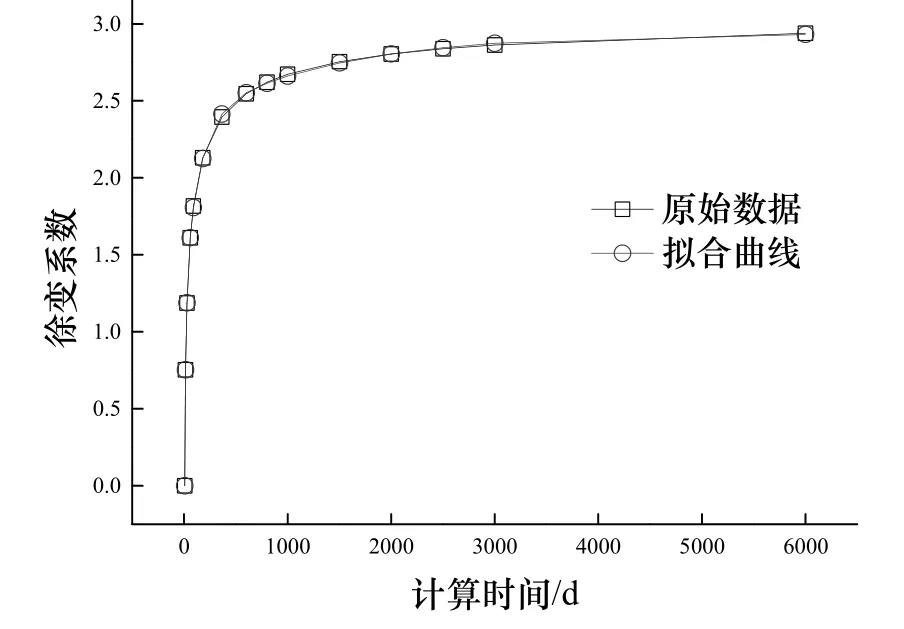
图1 徐变系数的拟合Fig.1 Fitting of creep coefficient
2 基于ABAQUS的实现方法
2.1 USDFLD子程序
USDFLD主要用于定义随场变量变化的复杂材料特性.本文主要用于定义随龄期变化的混凝土弹性模量.USDFLD通过子程序GETVRM在分析中进入结果数据库来提取相关的数据,在子程序中提取相应的轴向应力与应变来为后续膨胀应变的计算做准备.同时还可以定义状态模量,传递给其他子程序来使用.
2.2 UEXPAN子程序
UEXPAN可以计算时间变化引起的膨胀应变,本文用计算出的膨胀应变来模拟徐变收缩对轴向应变的影响,采用各向同性温度应变来模拟徐变应变.
通过子程序UEXPAN和USDFLD的结合来输入材料的徐变收缩特性,并采用较小的时间间隔(7d)来保证计算的精确性.对比不同的拟合结果可以发现,不同加载龄期下的拟合参数的结果是成比例关系的,可以通过内插法,求出其它相关加荷龄期下的参数,在子程序的编写中采用这一规律.同时子程序 UEXPAN中的膨胀应变采用递推的方法来计算,以避免考虑应力历史而需要的大量数据存储.
2.3 子程序的调用
把用户自定义场变量、状态变量、用户自定义膨胀加入结构材料的本构定义,同时将 MATLAB拟合好的数据写入文件.通过子程序USDFLD定义时间场变量及要用到的状态变量,并以此算出随时间变化的弹性模量.使用UEXTERNALDB子程序将文件中的数据写入矩阵中,供其它子程序UEXPAN调用.整个流程如图2:
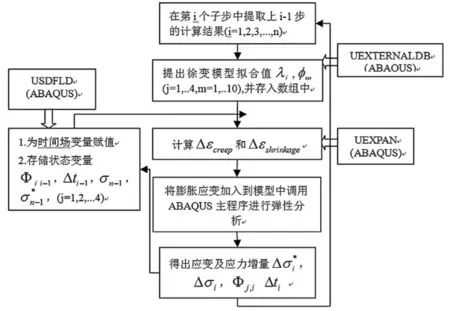
图2 计算程序流程Fig.2 The calculation process
3 配筋柱收缩徐变分析
3.1 模型参数
根据前面编制的子程序,采用 ABAQUS进行建模,对混凝土柱进行收缩徐变分析.计算方法为初应变法.混凝土柱长3 m,截面尺寸为250 mm×250 mm,混凝土强度为 C30,钢筋的弹性模量为2.03×105MPa,混凝土的弹性模量随时间变化.柱内配有4φ14钢筋,保护层厚度为25 mm,轴向压力为520 kN,轴压比为0.54.收缩极限应变为,shε∞=2.0×10-5,徐变系数为φ∞=3.0.模型图如图 3,采用实体模型,分离式模型建模.混凝土采用实体单元C3D8R,用三维桁架线性单元来模拟钢筋.钢筋与混凝土均处于弹性阶段,两者之间有较好的粘结,采用EMBED将两者绑定在一起.

图3 钢筋混凝土柱模型图Fig3. Diagram of reinforced concrete column model
徐变收缩预测模型采用 CEB-FIP1990规范提供的计算公式,并通过 MATLAB软件对徐变函数进行参数拟合.潮湿养护 7d后的混凝土开始自由收缩,得出混凝土及钢筋的应力重分布曲线如图 4和图 5,分单独考虑徐变和综合考虑徐变收缩两种情况.

图4 混凝土的应力Fig4. Stress of concrete

图5 钢筋的应力Fig5. Stress of rebar
从表1的结果可以看出,本文的计算结果与文献中的计算结果相当.本文计算的时长为2 100 d,且考虑了混凝土弹性模量的变化.由上述结果可以得出本文的计算结果是合理的,通过程序有效的实现了徐变收缩的计算.从图中也可以看出,单独考虑徐变时,混凝土的最终应力为6.69 MPa,钢筋的最终应力为162.77 MPa,徐变对混凝土总应力变化的影响为62.7%,对钢筋的影响为57.9%.

表1 计算结果对比/MPaTab.1 Comparison of the calculation results/MPa
3.2 参数分析
为了考虑配筋率、环境湿度及混凝土强度对配筋混凝土柱内力重分布的影响,分别采用不同的相关参数进行定量分析.本节采用的配筋率分别为0.723%、1.286%、2%、3.14%.湿度为50% ~ 80%,混凝土强度等级为 C30、C40.最后进行了不同计算规范对配筋混凝土柱内力重分布影响的分析.
3.2.1 截面配筋率
混凝土柱强度为C30,湿度为80%,配筋率分别为0.723%、1.286%、2%、3.14%,据此可以得出混凝土和钢筋的应力变化曲线分别如图6和图7所示:

图6 混凝土应力变化Fig6. Stress change of concrete
从图6和图7可以看出,随着配筋率的增加,混凝土的应力变化较大.持荷1 200 d以后,应力的变化幅度分别为 13.6%、23.9%、40.75%、51.8%.而钢筋的应力变化分别对应为初始应力的3.696、3.61、3.473、3.34倍.钢筋初始应力接近60 MPa,经过1200天徐变以后,其应力将达到230 MPa.柱的轴压比为0.542,若柱的轴压比再提高,则受徐变收缩的影响,钢筋的应力会达到屈服强度.由此可见,在进行结构设计时,柱的配筋率不宜过小,建议取2%~3%之间[6].否则在3~4年的使用期后,有可能使柱内的受压钢筋屈服,使钢筋过早进入塑性阶段.
当只考虑徐变时,随着配筋率的下降,徐变对混凝土总应力变化影响分别为 61.1%、63.5%、67.8%、70.4%,对钢筋总应力变化影响分别为57.2%、58.1%、63.5%、65.3%.可见随着配筋率的下降,钢筋的约束作用变小,徐变对混凝土柱内力重分布的影响增大.

图7 钢筋应力变化Fig.7 Stress changes of rebar
3.2.2 养护湿度
分别采用环境湿度为 50%、60%、70%、80%这四种情况进行计算.配筋率为1.286%,混凝土强度等级为C30.由计算结果可得混凝土和钢筋的应力变化曲线分别如图8和图9所示:

图8 混凝土应力变化Fig8. Stress change of concrete

图9 钢筋应力变化Fig.9 Stress changes of rebar
从图8和图9各曲线的相对关系可以很清楚的看到,湿度对钢筋混凝土柱构件应力重分布的影响相对较小,也趋于均匀化.当湿度在 50%~80%之间变化时,混凝土应力的变化量介于22.3%~32.1%之间,呈线性变化趋势.钢筋的应力变化相对较大些,为初始应力的3.4~4.37倍,因此也会导致钢筋应力过大,所以应注意在适当情况下考虑环境湿度的影响.
当只考虑徐变时,随着环境湿度的降低,徐变对混凝土总应力变化影响分别为 61.2%、64.5%、66.1%、70.8%,对钢筋总应力变化影响分别为57.2%、52.9%、49.3%、45.5%.可见随着湿度降低,徐变对混凝土柱内力重分布的影响变小.湿度对收缩的影响比较大,湿度越小,收缩越大.
3.2.3 混凝土强度
由于现有规范对高强混凝土材料的研究较少,所以本节主要考虑常用混凝土强度等级:C30和C40.配筋率为1.286%,湿度为80%,得出的混凝土与钢筋应力变化曲线如图11和图12所示.

图10 混凝土应力变化Fig.10 Stress changes of concrete
可以看出混凝土强度等级对混凝土柱内力重分布的影响较小.不同强度等级的情况下计算得出的混凝土应力相差很小,仅为1.68%,钢筋应力的差别为2.5%.因此可以忽略不计.
单独考虑徐变影响时,徐变对混凝土总应力变化影响分别为61.2%、60.5%,对钢筋总应力变化影响为55.6%、56.4%.可见混凝土强度的变化对徐变收缩的影响不大.

图11 钢筋应力变化Fig11. Stress change of rebar
3.2.4 不同规范计算方法
本节收缩徐变计算采用的公式为 ACI209、CEB-FIP1990和 GL2000,通过拟合相应的计算公式,得出拟合参数,然后进行计算,得到的曲线如图12和13所示.其中混凝土强度为C30,湿度为80%,配筋率为1.286%.

图12 混凝土应力变化Fig.12 Stress changes of concrete
从计算结果可以看出,不同规范得出的曲线的趋势有所不同,应力重分布的偏差很小.其中GL2000和CEB1990规范得出的曲线的趋势基本相同,在1 200 d以后,徐变收缩引起的应力重分布仍有增加的趋势,而 ACI209规范得出的结果在1 200 d以后基本趋于平缓,这与这三种规范的徐变收缩曲线的趋势相吻合.同时看到,CEB1990的计算结果比GL2000偏小,但总体来说,计算结果基本一致.相比于ACI209规范,其他两种能更好的反映后期收缩徐变对结构内力的影响.

图13 钢筋应力变化Fig13. Stress change of rebar
4 单层单跨框架收缩徐变分析
4.1 模型参数
跨度为6 m,柱高度为4 m,截面尺寸为600 mm×600 mm,梁截面尺寸为250×500mm.保护层厚度为30 mm,梁配筋采用420的钢筋,配筋率为1%,柱配有425钢筋,配筋率为0.545%.采用均布加载模式.混凝土与钢筋网模型如下图 14和图15所示,本节采用实体模型,采用分离式模型建模,混凝土采用实体单元C3D8R,用三维桁架线性单元来模拟钢筋.由于本节分析仅考虑结构受恒载影响,故钢筋与混凝土均处于弹性阶段,两者之间有较好的粘结,采用EMBED将两者绑定在一起进行分析.
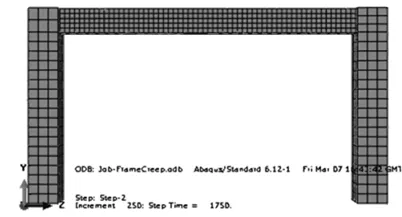
图14 混凝土模型Fig14. Model of concrete

图15 钢筋模型Fig15. Model of rebar
4.2 计算分析
4.2.1 弯矩变化分析
由第3节混凝土和钢筋的应力变化图可以看出,徐变对内力的影响主要发生在前两年,故计算时长选为 700 d.关于梁截面弯矩的计算,取跨中位置和距柱侧边0.2 m的位置.梁柱的加载龄期差值为15天,荷载大小为6.25 kN/m.考虑收缩徐变所得梁端弯矩变化如图17和18所示,其中关于混凝土弯矩与钢筋弯矩的计算均采用ABAQUS中的Free Body Cut选项,在场变量结果输出选项中选中节点力 NFORC,通过后处理,得出截面各节点力并对其形心取矩,即可求出其弯矩值.

图16 截面弯矩计算Fig16. Moment of cross section
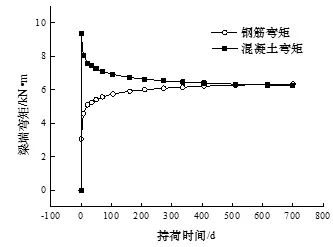
图17 截面弯矩重分布Fig.17 Moment redistribution of cross section

图18 总弯矩变化Fig18. Change of total moment
由图 18可以看出,在结构收缩徐变过程中,梁端弯矩的变化很小,有较小的增幅,可以忽略不计.由图 17可知梁截面处混凝土与钢筋的应力重分布不可忽略,在收缩徐变作用下,钢筋承担的弯矩在两年后超出混凝土.
为了更好的验证计算结果的合理性,采用MATLAB软件依照收缩徐变计算理论编写M文件,来计算相同结构的内力重分布,MATLAB的计算结果如图19和图20.

图19 梁端弯矩Fig19. Moment of beam end
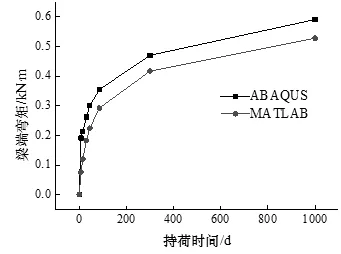
图20 徐变次弯矩对比Fig20. Contrast of creep secondary moment
由图 20可以看出两种计算方法得出的结果相差较小,而有限元模型相比杆系结构模型更能反映结构真实的内力重分布,从而验证了 ABAQUS计算结果的合理性.
4.2.2 加载龄期影响
当梁柱截面相同,具有相同的徐变收缩特性时,截面不会发生内力重分布.本节考虑梁柱加载龄期差异从0~60d变化时,梁端弯矩变化情况.

图21 梁端弯矩变化Fig21. Change of beam end
图 21显示了结构随加载龄期差异的增大,徐变变形减小,可以认为刚性变大,从而使梁端的弯矩增加,而跨中的弯矩减小.但因此而产生的次内力较小,变化幅度接近2%,可以忽略.
5 结论
(1)通过ABAQUS二次开发的徐变收缩计算程序,对配筋柱与单层单跨框架进行有限元计算分析,并与文献结果及 MATLAB程序的计算结果对比,可以看出计算结果较为合理,能够较好的反映收缩徐变对结构应力及内力重分布和位移的影响.
(2)通过配筋柱的参数分析,可以看出配筋柱的内力重分布对环境湿度及配筋率较为敏感,而混凝土强度对内力重分布影响不大,并对结构合理的配筋率给出参考性的建议.考虑了徐变和收缩各自的特点,发现徐变对配筋率较为敏感,随着配筋率提高,徐变的影响降低,而收缩对湿度比较敏感,湿度提高,收缩的影响降低,并且两者对混凝土强度均不敏感.同时对比了不同规范的计算结果,可以看出 CEB-FIP1990模型所得出的结构长期徐变收缩较大,能比较真实的预测结构的时变变形,同时CEB-FIP1990相比BP、B3模型来说公式相对简单,易于采用有限元软件实现.
(3)单层单跨框架内力重分布的大小取决于梁柱徐变的特性的差异情况,但从分析结果可以看出,这种变化非常小,可以忽略不计.
Reference
[1] BAŽANT Z P, LI G H. Comprehensive database on concrete creep and shrinkage[R]. Structure Engineering Report, 2008: 2-8.
[2] 丁文胜, 吕志涛, 孟少平, 等. 混凝土收缩徐变预测模型的分析比较[J].桥梁建设, 2004(6): 13-16.DING Wensheng, LÜ Zhitao, MENG Shaoping, et al.Analysis and comparison of prediction models for concrete shrinkage and creep[J]. Bridge Construction.2004(6): 13-16.
[3] BAŽANT Z P, BAWEJA S. Justification and refinements of model B3 for concrete creep and shrinkage 1. statistics and sensitivity[J]. Materials and Structures. 1995(7).
[4] 赵昕, 鄢兴祥, 孙华华, 等. 基于B3模型的巨型竖向构件收缩徐变分析[J]. 建筑结构, 2009(S1): 245-247.ZHAO Xin, YAN Xingxiang, SUN Huahua, et al.Shrinkage and Creep Analysis of Mega Vertical Members Based on Model B3[J].Building Structure, 2009(S1):245-247.
[5] HOWELLS R. W, LARK R. J, BARR B. I. G. A sensitivity study of parameters used in shrinkage and creep prediction models[J].Magazine of Concrete Research. Volume 57, Issue 10,2005: 589~602.
[6] 林超伟, 王兴法, 陈勤, 等. 长富金茂大厦混凝土收缩徐变分析及结构设计[J].建筑结构. 2011(05): 43-45.LIN Chaowei, WANG Xingfa, CHEN Qing, et al.Structural design and concrete shrinkage and creep analysis of Changfu Jinmao Building[J].Building Structure. 2011(05): 43-45.
[7] 周履, 陈永春. 收缩徐变[M]. 北京:中国铁道出版社,1994: 145-175.ZHOU LÜ, CHEN Yongchun. Creep and shrinkage[M].Beijing: China Railway Publishing House,1994: 145-175.
