基于非破坏性试验的既有结构评定方法

姚继涛，刘明璋，程凯凯

（西安建筑科技大学土木工程学院，陕西 西安 710055）

既有结构的可靠性评定方法主要有三类[1]：基于结构分析的评定方法、基于状态评估的评定方法和基于试验的评定方法．目前普遍采用的是前两类方法[2-5]，其中第一类方法中的试验主要为结构分析

提供实证性的参数，并不能直接用于评定既有结构；第三类方法中的试验则可直接用于评定，虽然该法存在技术、经济和实施周期上的困难，且有损害结构性能的风险，但在采用其他方法不能对既有结构作出准确评定时，基于试验的评定方法便成为一种可能的选择，特别是在评定大批量相似构件、重大工程结构和关键构件的场合．

为了满足评定对象后续使用的要求，该法需在非破坏性试验的条件下进行，因此必须在试验不充分的条件下推断抗力和作用效应的设计值．国际上对试验不充分条件下混凝土构件抗力的推断作了初步研究，建议根据50%设计荷载作用下构件残余变形的比例α推断构件的抗力．如对一般的钢筋混凝土构件，当α≤25%时判定其抗力满足要求[6]．但该法仅可给出抗力下限，不能对实际抗力作出最终推断，也未定量考虑推断中的不确定性，未考虑多个试件时的综合判定方法．就研究的整体规模和水平而言，我国学者在这方面的研究较少，本文的研究属于本学术领域的前沿课题，研究成果将为基于试验的既有结构评定方法提供参考．

本文将在确定既有结构非破坏性试验类型的基础上，建立试验不充分条件下单个试件抗力和作用效应的概率预测方法，进一步针对多个试件建立抗力和作用效应设计值的小样本推断方法，从而形成基于非破坏性试验的既有结构评定方法．该法的建立拓展了结构试验的应用领域，且该法较其他评定方法具有更为突出的实证性和针对性．

1 非破坏性试验的类型及试件的随机过程概率模型

1.1 非破坏性试验的类型

基于试验的既有结构的评定应采用非破坏性试验，以保证试验本身不严重损害结构的实际性能．按结构承载能力极限状态和正常使用极限状态的分类，对试件分别进行抗力、抗裂和挠度、裂缝宽度的非破坏性试验．按非破坏性试验的要求，对抗力和抗裂采用定态的试验方式，对挠度和裂缝宽度采用定荷的试验方式，即分别以试件达到设定状态和荷载达到设定水平作为试验结束的标志．

1.2 试件的随机过程概率模型

由于在试验过程中，测试值是随试件所发生的应变或所受荷载值的变化而变化的，而且不同试件在某一特定应变或荷载作用下的测试值是随机的，故本文对其采用随机过程的方法进行描述．根据所设定的试验类型可知，应分别建立荷载－应变（抗力为压应变，抗裂为拉应变）、挠度－荷载、裂缝宽度－荷载的随机过程概率模型，现以荷载－应变的概率模型建立过程为例说明．

根据文献[7]提出的抗力关于时间的随机过程概率模型的建立方法建立荷载关于应变的随机过程概率模型．记荷载为随机过程 {其中ε0为试件在自重等试验前荷载L0作用下的应变，εu为试件在极限荷载Lu作用下的应变．记荷载均值、标准差分别为 μL(ε)和σL(ε)，则自相关系数

式中：Cov[L ( ε +∆ε ),L(ε)]为荷载的自协方差，要通过统计分析获得其变化规律是很困难的．若假定为独立增量过程，即对于任意的荷载增量相互独立，则

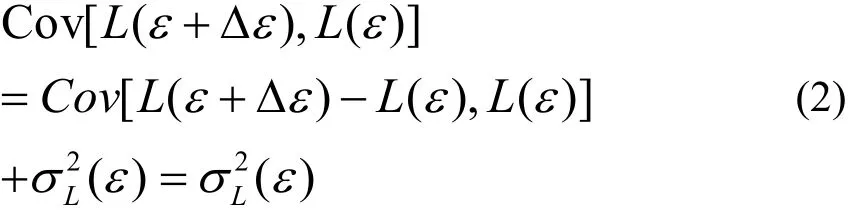
式（1）可变为

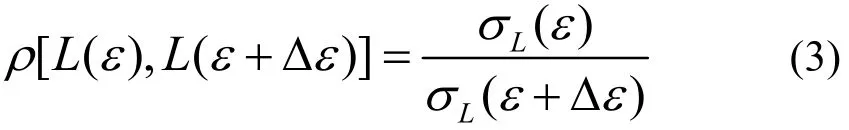
这时自相关系数可直接根据标准差确定，不必再对其进行统计分析．当然，上述所作假定是近似的，荷载增量之间会存在一定正相关性，但是相关程度较弱，而且根据式（2）可知，忽略荷载增量之间的相关性，将会减弱各应变点荷载间的相关性，这意味着其变异性增强，这对于分析结果是偏于保守的．所以，采用独立增量过程概率模型具有较好的可行性，并且可以得到较为保守的计算结果．

其他类型的随机过程概率模型的建立过程与上述方法相同，不再赘述．

2 单个试件抗力和作用效应的概率预测方法

非破坏性试验的结果只是揭示了试件在设定状态或设定荷载下的抗力或作用效应值，而非实际的抗力或作用效应，这时对试件是一种信息不充分条件下的推断．试件实际的抗力和作用效应是未知和随机的，且为不可重复试验下的个体随机现象，不能采用传统的基于可重复试验的概率方法．本文采用随机过程和条件概率的方法建立单个试件抗力和作用效应的概率分布，从而可对其作出概率预测．

2.1 单个试件抗力（或抗裂）的概率预测

首先根据结构理论估算试件在自重等试验前荷载0L作用下的应变0ε（对于抗力为压应变，对于抗裂为拉应变）；然后根据设定应变Tε确定试验中的应变增量ε∆，通过试验确定荷载增量L∆，这时设定应变Tε下的荷载值为

最后根据荷载－应变的随机过程概率模型和试验测试结果利用条件概率的方法确定试件抗力的概率分布．

假设荷载L为关于应变ε的独立增量随机过程，且其任意时点分布为正态分布，均值和标准差分别为 μL(ε)和σL(ε)．将极限荷载L(εu)在试验荷载值L(εT)=L下的条件概率分布作为试件抗力r的概率分布．由二维随机变量的条件概率分布可知试件抗力r的均值和标准差为[8]

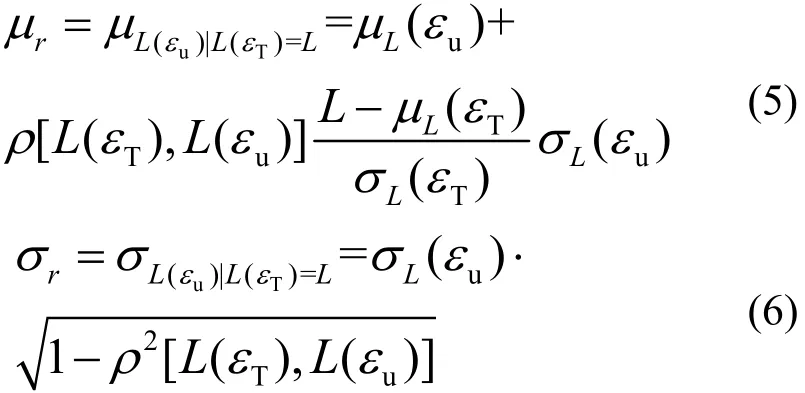
引入关系式(3)，则

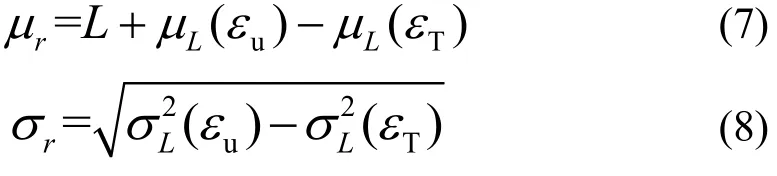
且抗力r服从正态分布．

根据抗力r的概率分布及其特征参数即可对试件的抗力值作出预测．从抗力r概率分布的特征参数中不难发现，其均值考虑了试件在设定应变下的荷载值，推断结果要更加贴近抗力的实际值，而且标准差比未经试验的结果小，说明抗力变异性变小．由此可见，基于非破坏性试验的抗力预测值比未经试验的结果要更加贴近实际值且具有较小的变异性．

若荷载L的任意时点分布为对数正态分布，则lnL的任意时点分布为正态分布，这种情况下抗力r的均值和标准差分别为

2.2 单个试件挠度和裂缝宽度的概率预测

单个试件挠度和裂缝宽度的概率预测过程与抗力和抗裂类似，以试件挠度的概率预测过程为例说明．

首先通过试验测定试件在设定荷载 LT作用下的挠度值αT；然后根据挠度－荷载的随机过程概率模型和试验测试结果利用条件概率的方法确定试件在设计荷载 Ld作用下挠度的概率分布．

假设挠度α为关于荷载L的独立增量随机过程，且其任意时点分布为正态分布，均值和标准差分别为 μα(L)和σα(L)．将挠度值α(Ld)在试验挠度值α(LT)=α下的条件概率分布作为试件挠度f的概率分布．由二维随机变量的条件概率分布可知f的均值和标准差为

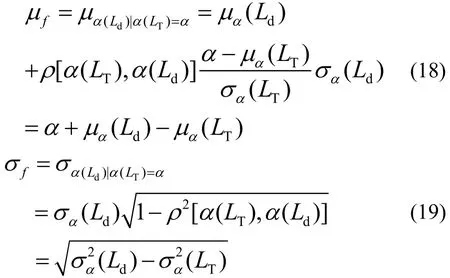
且f服从正态分布．

若挠度α的任意时点分布为对数正态分布，则lnα的任意时点分布为正态分布，这种情况下f的均值和标准差分别为

单个试件裂缝宽度的概率预测过程与挠度相同，不再赘述．

3 既有结构构件抗力和作用效应设计值的推断方法

在已经建立单个试件抗力和作用效应概率预测方法的基础上，将进一步针对多个试件建立抗力和作用效应设计值的小样本推断方法，从而最终建立起基于非破坏性试验的既有结构评定方法．依据上节内容可以求得单个试件抗力和作用效应的概率预测值，但并非其真实值，故无法采用传统的概率推断方法推断构件抗力和作用效应的设计值，现采用全概率的方法予以确定．

3.1 构件抗力和抗裂设计值的推断

3.1.1 抗力（或抗裂）R服从正态分布时的推断公式

假定构件抗力R服从正态分布，其均值和标准差分别为μR和σR，且σR（= σL(εu)）已知，则抗力设计值 Rd可表示为

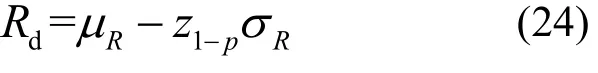
式中：z1-p为标准正态分布的上侧1 - p 分位值，p为构件抗力设计值的保证率．

从总体中抽取容量为n的样本，假定样本的观测值分别为 r1,… ,rn．由2.1节知单个试件抗力故样本均值也服从正态分布，其均值和标准差分别为

由式（8）知，σr1= σr2= … = σrn=σr，故σr改写为

因为r1,…,rn是容量为n的简单随机样本，故样本均值其概率密度函数又可以表示为

式中，均值μR是未知的，将其作为随机变量，则μR关于样本均值r的条件概率分布可表示为

则由全概率公式可得均值Rμ的概率密度函数

由函数形式可知均值μR服从正态分布服从标准正态分布，也即服从标准正态分布．令

根据区间估计法取置信度为C C时的下限估计值作为抗力设计值 Rd的推断值，即

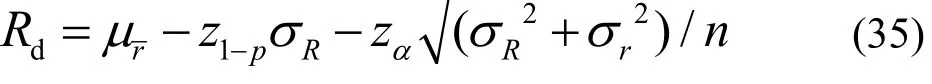
式中：zα为标准正态分布的上侧α分位值，α为显著性水平．

3.1.2 抗力（或抗裂）R服从对数正态分布时的推断公式

由上述推断可知当抗力R服从对数正态分布时，抗力设计值的推断值为

3.2 构件挠度和裂缝宽度设计值的推断

挠度和裂缝宽度设计值的推断与抗力和抗裂设计值的推断思路和方法是相同的，不再对其进行推导，仅将结果阐述于下．

3.2.1 挠度f(或裂缝宽度ω）服从正态分布时的推断公式

当挠度f服从正态分布时，其设计值的推断值为

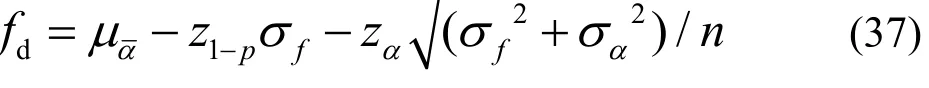
3.2.2 挠度f（或裂缝宽度ω）服从对数正态分布时的推断公式

当挠度f服从对数正态分布时，其设计值的推断值为

4 结论

(1)本文在确定既有结构非破坏性试验类型的基础上，采用随机过程和条件概率的分析方法建立了单个试件抗力和作用效应的概率预测方法；

(2)进一步针对多个试件，采用全概率的分析方法建立了抗力和作用效应设计值的小样本推断方法，从而最终建立起基于非破坏性试验的既有结构评定方法；

(3)该法的建立为既有结构的评定提供了更具实证性的试验辅助方法，从而更有效的保证结构、特别是重大工程结构和新型结构的可靠性，且该法的建立拓展了结构试验的应用领域，较其他评定方法具有更为突出的实证性和针对性；

(4)本文仅对此评定方法进行了理论上的阐述，其结果将通过试验予以验证，此部分内容将在后续研究中进行．

References

[1] 姚继涛, 马永欣, 董振平, 等. 建筑物可靠性鉴定和加固-基本原理和方法[M].北京: 科学出版社, 2003：19-22．YAO Jitao, MA Yongxin, DONG Zhenping, et al. The appraiser and reinforcement of reliability of buildings-the basic principles and methods[M].Beijing:Science Press,2003:19-22.

[2] 中华人民共和国住房和城乡建设部. (GB50292-1999)民用建筑可靠性鉴定标准[S].北京：中国建筑工业出版社, 1999．Housing and urban-rural development of the People's Republic of China.(GB50292-1999)Standard for appraiser of reliability of civil buildings [S]. Beijing:China Architecture &Building Press, 1999.

[3] 中华人民共和国住房和城乡建设部. (GB50144-2008)工业建筑可靠性鉴定标准[S]. 北京：中国计划出版社,2009．Housing and urban-rural development of the People's Republic of China. (GB50144-2008)Standard for appraisal of reliability of industrial buildings and structures[S]. Beijing:China Planning Press,2009.

[4] International Organization for Standardization.(ISO13822:2003) Bases for design of structures-Assessment of existing structures[S]. 2003.

[5] Joint Committee on Structural Safety. Probabilistic assessment of existing structures[S].2001.

[6] 潘景龙. 混凝土结构性能评定与检测[M].哈尔滨: 黑龙江科学技术出版社, 1997: 115-123.PAN Jinglong.The performance assessment and test of concrete structures[M].Harbin:Heilongjiang Science& Technology Press,1997:115-123.

[7] 姚继涛, 刘金华, 吴增良．既有结构抗力的随机过程概率模型[J].西安建筑科技大学学报:自然科学版, 2008,40(4): 445-449．YAO Jitao, LIU Jinhua, WU Zengliang.Model for stochastic resistance of existing structures[J].J.Xi'an Univ.of Arch & Tech.: Natural Science Edition,2008,40(4):445-449.

[8] 刘次华, 万建平. 概率论与数理统计[M].北京: 高等教育出版社, 2008: 94-96．LIU Cihua, WANG Jianping.The probability theory and mathematical statistics[M].Beijing: Higher Education Press,2008:94-96.

[9] 贡金鑫, 魏巍巍. 工程结构可靠性设计原理[M]. 北京：机械工业出版社, 2007: 303-304．GONG Jinxin, WEI Weiwei. The design principle of reliability of engineering structure[M].Beijing: China Machine Press,2007:303-304.