基于Perform-3D的型钢再生混凝土框架-填充墙结构力学性能分析

薛建阳，席 宇，高 亮

（西安建筑科技大学土木工程学院， 陕西 西安710055）

再生混凝土力学性能、耐久性能、变形性能等均低于普通混凝土[1]，使得再生混凝土结构受力性能较普通混凝土结构差，而组合结构具有承载力高、抗震性能好等优点，将再生混凝土应用于组合结构中，可以使结构具有组合结构的优点，弥补了再生混凝土的不足，同时，可实现资源的再利用，节能环保，达到组合结构的可持续发展．目前，国内外对型钢再生混凝土梁、柱构件进行了试验研究，文献[2]对 10根型钢再生混凝土梁的抗剪性能试验结果表明：剪跨比是梁构件受剪承载力及破坏形态的主要影响因素；文献[3]对 17根型钢再生混凝土柱进行了低周反复荷载作用下抗震性能试验研究，结果表明：型钢再生混凝土柱抗震性能良好，剪跨比、轴压比以及体积配箍率是影响构件抗震性能的主要因素．以上研究主要是针对型钢再生混凝土梁、柱构件，而对型钢再生混凝土框架整体结构的研究却较少．如今，在框架结构中普遍使用的实心黏土砖填充墙材料正逐步被一些新型砌体材料(包括普通混凝土空心砌块、再生混凝土空心砌块、粉煤灰砌块、加气混凝土砌块等)所取代，对这种新型填充墙抗震性能的研究也不多见[4]．为了研究型钢再生混凝土框架—再生混凝土空心砌块填充墙这种新型结构的力学性能，本文基于该结构在低周反复荷载作用下的试验，通过有限元软件Perform-3D进行建模，分析轴压比、宽高比对结构力学性能的影响．

1 试验概况

1.1 试件设计

3榀试件均按1:2.5缩尺设计的单层单跨型钢再生混凝土框架，缩尺框架模型层高1 440 mm，跨度2 280 mm．梁截面尺寸bh×=150 mm×240 mm，柱截面尺寸为bh×=180 mm× 240 mm．框架柱内配置14号工字钢，梁、柱纵筋选配HRB400，箍筋选配 HRB335．框架及梁、柱截面几何尺寸、配筋及配钢形式如图1所示．试验采用再生骨料取代率为 100%的再生混凝土，根据试验测得再生混凝土立方体抗压强度平均值为52 MPa．再生混凝土砌体中砂浆采用 Mb10，根据试验测得再生混凝土砌块的抗拉强度为2.7 MPa，抗压强度为5.6 MPa．试件设计参数见表1，钢筋和型钢的力学性能见表2．

图1 试件几何尺寸及配筋、配钢形式（单位：mm）Fig.1 Geometry and steel layout of specimens（unit：mm）

表1 试件设计参数Tab.1 Parameters of specimens

表2 钢筋及型钢力学性能Tab.2 Properties of steel

1.2 加载制度

加载时，首先在柱顶施加竖向荷载至设计值（对应于试件SRRCF1、SRRCF2、SRRCF3的轴压力设计值分别为500 kN、750 kN、500 kN），并保持恒定，然后在梁端施加水平反复荷载，水平荷载作用点位置距柱底为1 320 mm．试验加载模式采用力-位移混合控制，即结构屈服前为荷载控制，每级循环1次，结构屈服后为位移控制，按屈服位移的倍数进行加载，每级循环3次，直至试件层间侧移角达到1/20结束试验．试验加载装置如图2所示．

图2 试验加载装置Fig. 2 Test setup

2 有限元建模

运用有限元软件 Perform-3D对试件进行非线性分析,建模过程包括材料本构关系的选取、定义边界条件与荷载施加方式、单元类型选取和网格划分．

2.1 材料本构关系

通过 Perform-3D /Material /Inelastic Steel Material Non-Bucking 模块进行钢筋及钢材本构关系的定义，采用双线性强化模型．通过Perform-3D/Material/Inelastic ID Concrete Material模块对无约束再生混凝土进行本构关系的定义，采用软件所提供的三折线关系，不考虑受拉强度，考虑强度损失（即曲线的下降段）；而对约束再生混凝土采用Mander模型[5]进行本构关系的定义，采用三折线关系，不考虑受拉强度，考虑强度损失．将再生混凝土砌体对框架的作用等同于斜压杆效应[6]，通过Perform-3D/Material/Diagonal Compression Material for a Wall模块对砌体选用斜压杆模型，采用三折线关系，考虑强度损失；通过Perform-3D/Material/Inelastic Shear Material for a Wall模块进行砌体剪切材料砂浆本构关系的定义，采用三折线关系，考虑强度损失．

2.2 边界条件与荷载施加方式

在 Perform-3D/NODES模块中定义框架与基础、基础与地面均为固结，避免加载过程基础移动．荷载的施加通过两个步骤实现，首先施加竖向荷载，并保持恒定，然后施加水平荷载．为保证计算结果收敛，模型加载采用位移控制的模式，允许层间最大位移角为1/20．

2.3 单元类型选取和网格划分

基于钢筋、钢材、再生混凝土及再生混凝土砌体材料本构关系的定义，梁单元、柱单元均采用塑性区模型[7]，墙单元采用通用墙单元模型．对于梁、柱构件截面的本构模型采用纤维模型[8]进行定义．图3为纤维截面[9]的划分，梁截面被划分为条带纤维，柱截面被划分成空间纤维单元，型钢的纤维模拟通过面积等效的方法将其离散成钢筋纤维．

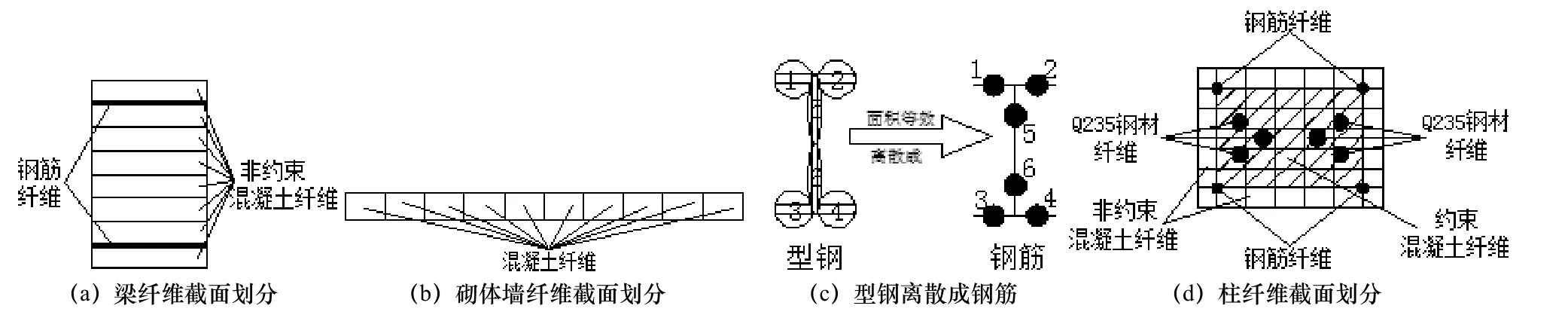
图3 纤维截面划分Fig. 3 The division of fiber cross section

3 试验结果与计算结果对比分析

3.1 骨架曲线分析

通过有限元软件Perform-3D计算分析，可得到基底剪力与顶点相对位移角的关系曲线，将其转换为试件承载力与顶点位移的关系曲线，即 F-D曲线．图4为试件试验与模拟F-D曲线对比及计算刚度与试验实测刚度对比．

从图4中F-D曲线可以看出，在弹性阶段，结构计算刚度较试验值偏大，后期下降段强度的计算值与试验值有一定偏差，但最终二者的发展趋势趋于一致．产生上述偏差的原因主要是：（1）在有限元模拟过程中，未考虑型钢、钢筋与混凝土之间的粘结滑移，导致有限元模拟的初期刚度值较大；（2）试验采用循环往复加载的方式，而有限元模拟采用的是单调加载方式，使得模拟得到的混凝土损伤程度不如试验严重，刚度下降缓慢[10]．从图4中K-D曲线可以看出，结构屈服前，刚度计算值较试验值偏高．这是由于试件屈服前产生大量裂缝，包括墙体的开裂、混凝土的开裂等，导致其刚度退化较快．但随着试件进入弹塑性工作阶段，刚度退化明显减慢．随着塑性的发展，试验与模拟得到的刚度退化曲线逐渐趋于一致．从表3试验与计算特征荷载值的对比中可以看出，屈服荷载、峰值荷载及破坏荷载的计算值均较试验值大，主要是由于有限元模拟混凝土的损伤程度不如试验情况下严重．

图4 F-D曲线对比及刚度退化对比Fig. 4 Comparison of F-D curves and comparison of stiffness degradation curves

表3 试验值与计算值的对比Tab.3 Comparison of the test results with the calculating results

3.2 延性分析

通过试验得到的F-D曲线并采用“通用屈服弯矩法”[11]确定屈服位移，由公式μ=∆u/∆y（∆u为试件的破坏荷载对应的位移；Δy为试件的屈服位移)求得各试件的位移延性系数μ，结果见表3．从表3中可以看出，有限元模拟的结果与试验结果基本吻合．试件的位移延性系数在 4.00～6.18 之间，满足一般延性框架延性系数大于3的要求，说明该

结构具有良好的延性，即在荷载不显著下降的情况下，具有良好的塑性变形能力．

3.3 出铰顺序分析

框架结构中塑性铰出现的位置和顺序不同会导致结构产生不同的破坏模式．有限元模拟和试验实测得到的结构出铰位置和顺序如图5a所示，模拟与试验结果相符．从图中可以看出，塑性铰首先出现在梁端，而柱端塑性铰的出现均在梁端塑性铰出现之后．

针对实际工程中底层大开间、上层设有隔墙的结构，以及同一层中墙体不同布置的结构，本文进行了有限元模拟，分析得到以上两种结构的出铰顺序如图5b、5c所示．可以看出，所有柱端出铰也均在梁端出铰之后，这一结果表明该型钢再生混凝土结构为“强柱弱梁”型结构，符合抗震设计要求．

图5 出铰顺序对比Fig. 5 Comparison of subsequence of plastic hinges

4 参数分析

为了更广泛地研究相关参数对结构力学性能的影响，采用有限元软件Perform-3D分析了轴压比n、宽高比B/H对结构承载力、刚度以及延性的影响，计算结果如图6和表4、表5所示．

图6 轴压比、宽高比对F-D曲线的影响Fig. 6 F-D curves with different axial compression ratios and different width-height ratios

表4 轴压比对结构承载力及延性的影响Tab.4 Influence on load-bearing and ductility under different axial compression ratios

表5 宽高比对结构承载力及延性的影响Tab.5 Influence on load-bearing and ductility under different width-height ratios

从图6a、表4可以看出：随着轴压比的增大，结构的水平承载力有了一定提高．轴压比为0.2时，结构承载力为439.98 kN，当轴压比提高到0.4、0.6时，其承载力相应提高6.7%和9.6%．在弹性工作阶段，不同轴压比下的曲线几乎重合，随着轴压比增大，结构初始刚度略有提高；在塑性工作阶段，轴压比对曲线的下降段有一定影响．这是由于轴压比增大会延缓混凝土裂缝的产生和开展，但是混凝土一旦开裂，随型钢和钢筋屈服，结构塑性变形会迅速增大，结构刚度退化加快，其所承受的荷载下降也随之加快．随着轴压比的增大，结构的位移延性系数由6.99降低到4.30，延性变差．这主要是由于轴压比增大，在加载后期，试件承载力迅速降低，导致试件的破坏位移减小．

从图6b、表5可以看出：随着宽高比的增大，结构的水平承载力有所提高．试件宽高比为 1.2:1时，结构的承载力为 379.22 kN，当宽高比增大到1.7:1、2.2:1时，结构的承载力相应提高了 23%和27%，这是由于随着填充墙宽度的增大，结构刚度增大，其对框架的约束作用加强导致结构的承载力有所提高．同时，结构的初始刚度有明显的提高，但在加载后期，结构的刚度退化加快，这是由于墙体开裂后逐渐退出工作，结构的刚度退化较严重．随着宽高比的增大，结构的位移延性系数由6.29降低到4.30，表明结构的延性变差．这主要是由于宽高比较大时，试件最大荷载下降较快，导致极限位移减小，结构延性降低．

5 结论

通过三维非线性有限元软件 Perform-3D并结合纤维模型理论对型钢再生混凝土框架-再生混凝土空心砌块填充墙结构进行建模分析，研究在水平荷载作用下结构的出铰机制，以及轴压比、宽高比对结构水平承载力、刚度及延性的影响，得出以下主要结论：

（1）随着轴压比的增大，结构的水平承载力有所提高；结构初始刚度略有提高，但在加载后期，结构刚度退化加快；结构的延性降低．

（2）随着宽高比的增大，结构的水平承载力有所提高；结构的初始刚度有明显提高，但在加载后期，结构刚度退化加快；结构的延性降低．

（3）结构的出铰位置与顺序表现为先梁端后柱端，符合“强柱弱梁”的抗震设计要求，延性较好，具有较好的塑性变形能力．

References

[1] 肖建庄. 再生混凝土[M]. 北京: 中国建筑工业出版社,2008.XIAO Jianzhuang. The recycled concrete[M]. Beijing:China Building Industry Press, 2008.

[2] 薛建阳, 王秀振, 马辉, 等. 型钢再生混凝土梁受剪性能试验研究[J]. 建筑结构, 2013, 43(7): 69-72.XUE Jianyang, WANG Xiuzhen, MA Hui, et al.Experimental study on shear performance of steel reinforced recycled aggregate concrete beams[J].Building Structure, 2013,43(4): 69-72.

[3] 马辉. 型钢再生混凝土柱抗震性能及设计计算方法研究[D]. 西安: 西安建筑科技大学, 2013.MA Hui. Research on seismic performance and design calculation theories of steel reinforced recycled concrete columns [D]. Xi'an: Xi'an University of Architecture &Technology, 2013.

[4] 张杰, 郭子雄. 再生混凝土填充墙在中国的研究与应用前景[J]. 建筑技术开发,2001,8(5): 12-14.ZHANG Jie, GUO Zixiong. Research and application of new environmental filled-wall material in China[J].Building Teghnique Development, 2001, 8(5): 12-14.

[5] MANDER J B, PRIESTLEY M J N, PARK R.Theoretical stress-strainmodel for confined concrete[J].Journal of Structural Engineering, 1988, 114(8): 1804-1826.

[6] 苗凤. 填充墙对钢筋混凝土框架结构动力性能的影响[D].长沙: 湖南大学, 2006.MIAO Feng. The Effect of Infill Walls On the Dynamic Behavior of Reinfroced Concrete Frames[D]. Changsha:Hunan University,2006.

[7] ATC-72. Guidelines for cyclic seismic testing of components of steel structures[R]. Redwood City(CA):Applled Technology Council, 1992.

[8] ZERIS C.A, MEHIM S.A. Analytical Predition of Biaxial Response of a R/C shake Table Model [C]//U.S. National Conference on Earthquake Engineering, 1986,Vol.

[9] 梁兴文, 叶艳霞. 混凝土结构非线性分析[M]. 北京:中国建筑工业出版社, 2007.LIANG Xingwen, YE Yanxia. Nonlinear analysis of reinforced concrete structures[M]. Beijing: China Building Industry Press, 2007.

[10] 薛建阳, 刘祖强. 实腹式型钢混凝土异性柱边框架拟静力试验及有限元分析[J]. 建筑结构学报,2012,33(8):23-30.XUE Jianyang, LIU Zuqiang. Quasi-static test and finite element analysis on solid-web steel reinforced concrete exterior frame with special-shaped columns[J]. Journal of Building Structures, 2012, 33(8): 23-30.

[11] 熊仲明, 王社良. 土木工程结构试验[M]. 北京: 中国建筑工业出版社, 2006.XIONG Zhongming, WANG Sheliang. Test for civil engineering structure[M]. Beijing: China Building Industry Press, 2006.