使用似然比D2统计量的题目属性定义方法*

喻晓锋 罗照盛 高椿雷 李喻骏 王 睿 王钰彤

(1江西师范大学心理学院, 南昌 330022) (2亳州师范高等专科学校, 亳州 236800)

1 引言

我国中长期教育改革和发展规划纲要(2010-2020年)明确提到：要注重因材施教, 要改进教育教学评价, 探索促进学生发展的多种评价方式。要做到因材施教, 首先就必须深入地了解学生的认知特点, 对其长处和短处进行诊断性分析, 即实施认知诊断评价(也简称认知诊断)。相对于其它的评价形式, 认知诊断评价不但能提供被试在测验上的总体评价指标, 而且能提供被试在测验领域上的详细的诊断报告。著名的“分数减法”数据(Tatsuoka,1990)中包含 20个题目, 界定了将整数化为分数、从带分数中分离出整数、在减法运算前进行化简等8个属性。如果某被试的属性掌握模式为[1 0 0 0 0 0 0 0], 表明该被试只掌握了第1个属性(即将整数转化为分数), 对其他7个属性都没有掌握。有了诊断性分析报告, 就可以进行有针对性的补救教学和学习。由此可见, 认知诊断报告中可提供丰富的信息,对被试的学习、教师的教学和教学效果的评价都有很重要的参考作用。

属性是指测验所考察的被试的潜在特质, 包括知识、技能、策略等(Leighton, Gierl, & Hunka,2004)。Q矩阵(Tatsuoka, 1983)描述了测验中的所有题目和属性之间的关联关系, 通常用1来表示题目考察了某属性, 用0来表示题目没有考察某属性。丁树良等人对 Q矩阵理论进行了深入研究(丁树良,罗芬, 汪文义, 2012; 丁树良, 毛萌萌, 汪文义, 罗芬, Cui, 2012; 丁树良, 汪文义, 罗芬, 2012; 丁树良, 汪文义, 杨淑群, 2011; 丁树良, 杨淑群, 汪文义, 2010)。Q矩阵的建立包括题目属性的定义和题目属性向量的验证。被试在测验属性(通常有多个)上的掌握情况就构成了被试的属性掌握模式。

认知诊断模型借助Q矩阵, 以作答数据为基础去推断被试的属性掌握模式。题目属性(在本文中,如无特别说明, 题目属性是指题目的属性向量)的定义和认知诊断模型对认知诊断评价很重要。测验中题目属性向量(即Q矩阵)的定义是否正确对于认知诊断模型的识别和被试的分类都是十分关键的(Rupp & Templin, 2008)。通常情况下, 题目属性是由领域专家根据自己的知识或经验进行定义的, 但这容易受到专家主观因素的影响, 从而导致题目属性的定义出现偏差。上述“分数减法”测验(Tatsuoka,1990), 直到今天, 其题目属性定义仍然存在争议。可见, 题目属性的定义是一件非常困难和关键的工作。

Q矩阵的建立包括题目属性的定义和题目属性向量的验证。一方面, 研究者们研究了测验题目固定(即每位被试作答的项目相同)时 Q矩阵的修证。de la Torre (2008)提出了一个基于经验的验证Q矩阵的方法, 即δ法, 该方法研究了题目属性向量取不同值时, 通过该题目的猜测参数和失误参数的变化情况(设置阈值)来进行判断题目属性向量的正确性; 涂冬波, 蔡艳和戴海琦(2012)研究了基于DINA模型的 Q矩阵修正方法, 即γ法, 通过对猜测或失误参数过大(设置阈值)的题目进行检验, 来判断该题目是否考察了某属性。上述研究在确定正确题目属性向量的标准时存在主观性。DeCarlo(2011, 2012)利用贝叶斯方法来识别 Q矩阵中存在的错误, 但是该方法没有为存在错误的题目提供建议的属性向量。Liu, Xu和Ying (2011, 2012)提出从作答数据中推导Q矩阵的方法, 构建了评价Q矩阵的统计量, 并建立了相应的理论基础, 这为客观地推导Q矩阵迈出了重要的一步。模拟实验结果表明,Liu等的方法有比较好的估计准确率, 但是 Liu等的方法在执行上比较费时。Xiang (2013)在Liu等人(2011, 2012)的基础上, 将 Q矩阵中的元素当作连续变量进行估计, 通过截断点转换成0, 1数据, 但是相对于Liu等人(2011, 2012)的方法, 这种方法在准确率上并没有优势。

另一方面, 也有研究者们研究了计算机自适应测验形式下题目参数和题目属性向量的估计。汪文义等人(汪文义, 丁树良, 2010; 汪文义, 丁树良,游晓锋, 2011)研究了在给定“新题(即题目属性未知的题)”的题目参数以及被试在“旧题(即题目属性已知的题)”和“新题”作答的基础上, 使用极大似然估计方法、边际极大似然估计方法以及交差方法来估计“新题”的属性向量。陈平和辛涛(2011a)研究了“新题”参数的在线标定技术, 他们将“新题”随机或自适应分配给被试, 通过被试在“旧题”上的作答,估计出被试的属性掌握模式和题目参数, 然后条件估计“新题”的题目参数。陈平和辛涛(2011b)研究了基于“新题”和“旧题”作答数据联合估计“新题”的题目参数和属性向量。上述研究都是在得到被试的属性掌握模式之后, 或者已知题目的属性向量来估计题目的参数, 或者已知题目的属性向量，“在线估计”题目的参数, 或者是以在线的方式联合估计题目的属性向量和题目参数。

在现代教育和心理测验中, 需要对所选择的项目反应模型与作答反应数据进行拟合检验, 来评价所使用的模型与数据之间的拟合情况。通常是把模型的预测值(比如期望得分)和实际观察值(比如实际得分)之间的残差作为统计量, 这个残差的不同计算方法就构成了不同的拟合统计量, 常用的有Bock的卡方统计量(Bock, 1972), Yen统计量(Yen,1981), 似然比 G统计量(McKinley & Mills, 1985)等。

本研究受项目反应理论(Item Response Theory,IRT)中题目和数据拟合检验方法的启发, 提出本研究的逻辑假设：在认知诊断评价中, 测验中的题目属性定义与作答反应数据的拟合情况, 应该也是可以按照类似IRT中的模型—资料拟合检验的方法进行检验的, 选择拟合指标最好的题目属性向量作为当前作答反应数据所对应的题目属性定义。基于这种逻辑假设, 本文提出一种简单易懂的定义和验证题目属性向量的方法：即使用似然比统计量来对被试的属性掌握模式、题目参数和题目的属性向量进行在线的联合估计。

2 IRT下的模型拟合度评价方法

一般来说, 数据与模型的拟合优度可评价观察结果与期望结果之间的一致性程度(McKinley &Mills, 1985; Orlando & Thissen, 2000)。在IRT框架下, 通常评价每个题目作答反应数据与模型的拟合性的过程如下：

(1)在作答数据和所选择的 IRT模型的基础上,估计题目参数和能力参数;

(2)根据被试的能力估计值构造能力分组, 通常按能力分组的组数是一个比较小的整数, 比如10, 在同一组内的被试的能力值接近;

(3)根据能力估计值和作答数据, 为每个能力组被试计算观察得分分布, 即计算每个能力组被试对题目实际的正确作答概率;

(4)根据能力估计值、选定的IRT模型, 计算各被试组在题目上的期望得分分布, 即计算各能力组被试对题目的期望正确作答概率;

(5)比较观察得分分布和期望得分分布之间的差异。

其中第(5)步中通常采用某种卡方统计量来进行比较, 这里只介绍与本文相关的似然比G统计量。

这里的g是题目j在能力全距内将被试所分的组的个数,p和π分别是第i组被试在题目j上的实际正确作答概率和期望正确作答概率。N和r分别是第i组被试的总人数和其中实际正确作答题目j的人数, 并且有公式(2)成立。

π是根据第i组被试的能力平均值计算出来的正确作答概率(期望正确作答概率)。当采用边际极大似然估计方法来估计题目参数时, G服从自由度为 g的 χ分布(du Toit, 2003)。

3 使用D2统计量来估计题目属性向量和Q矩阵

本文在G统计量的基础上进行修改得到D统计量, 并采用 D统计量检验题目属性与作答反应数据之间的拟合度, 进一步确定合理的题目属性向量。这里以DINA模型为例来说明估计题目属性向量的具体过程, 该方法可以很容易地扩展到其它认知诊断模型上。

3.1 DINA模型

“确定性输入, 噪音‘与’门” (Deterministic Inputs, Noisy And “gate”, DINA )模型(de la Torre,2008, de la Torre, 2009, Junker & Sijtsma, 2001, Rupp& Templin, 2008)是近年来受到广泛关注的认知诊断模型之一。DINA模型是一个非常“节省”的模型,每个题目只有两个参数, 分别是失误参数(slipping parameter, s)和猜测参数(guessing parameter, g)。失误参数s表示被试掌握了题目所考察的属性, 但是错误作答的概率; 猜测参数g表示被试未完全掌握题目所考察的属性, 但是正确作答的概率。DINA模型是一种“连接”的、非补偿的模型。“连接”是指在不考虑猜测和失误的情况下, 被试必须完全掌握题目所考察的属性才能正确作答题目, 这种情况下的作答称为理想作答, 用η表示。

公式(3)表示被试i (属性掌握模式为α)在题目j (属性向量为q)上的理想作答。当已知题目j的参数分别为s和g, 则被试i在题目j上的正确作答概率可表示为公式(4)。

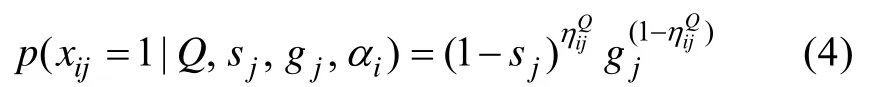
3.2 DINA模型下的D2统计量

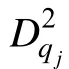
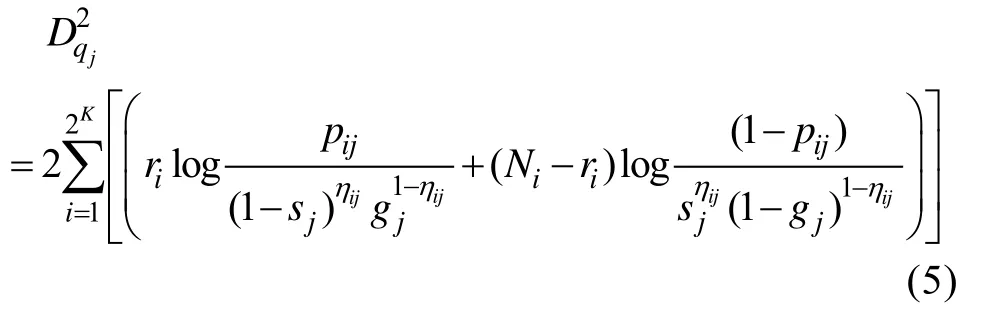
式(5)中, K是测验考察的属性个数, DINA模型不考虑属性之间的相互关系, 测验将被试分成 2组。η表示在第i组被试在题目j上的理想作答(即不考虑猜测和失误时的作答), 取值0或1。N是第i组被试的总人数, r是 N中正确作答题目 j的人数。 s和 g分别是题目j的失误参数和猜测参数。p是第i组被试中实际的正确作答题目j的人数比例, p的计算见公式(2)。

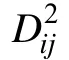
3.3 Q矩阵和题目参数的在线估计算法

为方便介绍, 将采用 D似然比统计量的在线估计(Likelihood Ratio Online Estimation)算法命名为LROE算法。假设测验共考察K个属性, 不考虑属性之间的相互关系(即假设属性之间的层级结构是独立型), 则一共有 2种属性掌握模式(即有 2类被试), 每个被试属于其中的一类。如无特别说明,本文用大写字母 Q带下标的方式表示题目的属性向量集合, 用小写字母q带下标的方式表示某个题目的属性向量。

假设已经有少部分题目属性被正确定义, 称这部分题目的集合为“基础题”, 记为Q。属性向量未定义的题目集合为“新题”, 记为 Q, Q中的题目属性向量需要借助于 Q中的题目来界定。这里采用“增量”的方式每次从“新题”中选择一个题目(记为 q)累积加入到 Q中, 然后联合估计Q的题目参数、q的属性向量和题目参数, 直到所有新增题的属性向量和参数都被估计。

下面介绍详细的估计过程, LROE算法的过程包括两大步骤, 具体内容如下：

第一步：估计所有新增题目的属性向量和题目参数, 包括以下几个具体步骤：

(1)从 Q中选择一个题目, 记为 q, 将 q加入到Q中, 并且把q作为第1个题目。

(2)以 Q、q和作答数据为基础, 使用MMLE/EM算法(de la Torre, 2009)联合估计题目参数和被试的属性掌握模式。

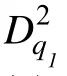
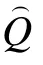
对每个新增题目的估计过程, 需要计算 D统计量和调用MMLE/EM算法的次数都为2-1次。

第二步：对所有题目的属性向量和题目参数进行校正, 包括以下几个具体步骤：

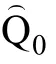
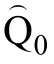
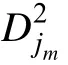
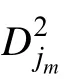
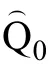
(7)算法结束, 得到Q矩阵的最终估计值。

以上第一步对每个题目进行估计时, 每次是“增量”式地选择一个新题进行估计, 当包含的“基础题”较多时, 这种方法会有利于对每个新题的估计, 因为此时数据中包含较多有用的信息和较少的噪音信息。但是当“基础题”的数量较少时, 即数据中包含的信息不足以对某些新题进行估计, 可能会导致出现偏差。

第二步会在第一步估计得到的 Q矩阵基础上(此时的Q矩阵中包含的错误较少)对每个题目进行第二次“校正”, 相当于使用数据对题目进行了双重“校正”。因此, 整个LROE算法包含两个步骤：先基于第一步算法对每个新题完成估计, 然后对整个Q矩阵进行校正。在第二步中, 算法每完成从步骤(5)到(10)的一次执行称为一次迭代, 为了防止估计程序执行时间太长或不收敛, 可以通过设置最大迭代次数来避免(当“基础题”较少或被试人数较少时可能会出现程序执行时间较长或不收敛的情况)。

4 模拟研究

为了研究本文所提出的算法在不同条件下的表现, 考虑的因素有三个：属性个数、作为基础的题目个数和被试人数。

4.1 研究设计

4.1.1 Q矩阵的模拟与初始Q矩阵

Q矩阵的真值与Liu等人(2012)相同, 一共有三个, 分别记为Q、Q和Q, 如图1所示。Q、Q和Q中的属性个数分别为3, 4和5, 题目个数都是20。

图1 模拟的真实Q矩阵(引自Liu等(2012))

4.1.2 题目参数的模拟

题目参数

s

和

g

按均匀分布模拟, 取值区间为[0.05,0.25]。

4.1.3 被试的属性掌握模式和作答的模拟

被试总体按均匀分布模拟, 即每种属性掌握模式的人数相近, 分别产生 400、500、800和 1000人, 共四种情况。使用公式(4), 在题目参数、题目属性向量和被试属性掌握模式的基础上模拟被试作答, 即将正确作答概率与均匀分布的随机数比较,当正确作答概率大于随机数时为正确作答, 否则为错误作答。

4.1.4 基础题和初始Q矩阵

基础题的个数一共有8, 9, 10, 11, 12共5种情况, 基础题的选择方式是从Q矩阵中随机选取。初始Q矩阵是作为估计程序的输入, 第一次迭代时的初始Q矩阵只包含基础题, 之后的初始Q矩阵都在前一次的基础上增加一个新题。

本研究中三个因素(Q矩阵、基础题的个数和被试人数)的水平分别为3, 5和4, 一共有3×5×4=60种情况。

4.1.5 评价指标

因为由

K

个属性组成的属性向量有 2种, 在定义错误的情况下, 题目的属性向量有 2-2(不能是全0向量和正确的向量)种可能。对于结果的评价采用与Liu等(2012)中相同的方式, 即从100批模拟数据中算法恢复正确 Q矩阵的次数作为评价指标,恢复次数越接近100, 表明算法恢复的成功率越高。

具体的研究过程如下：

(1)分别在 Q, Q和 Q下, 模拟题目、被试和作答;

(2)针对每种不同个数的“基础题”, 产生100个只包含“基础题”的初始Q矩阵(即每次从20个题目中随机抽取预定个数的题目作为“基础题”, 这样使得100个初始

Q

矩阵中包含的基础题个数相同, 但是具体题目不同。从而产生不同的初始Q矩阵, 以此作为估计算法的出发点, 下一次迭代的输入总是在前一次初始Q矩阵的基础之上加入一个新题);

(3)使用 LROE算法的第一步, 每次选择一个需要估计的新题q, 补充到初始Q矩阵Q中, 作为算法的出发点去估计q, 直到所有的新题都被估计。

(4)使用 LROE算法的第二步对包含所有题目的Q矩阵进行校正。

(5)计算算法从 100个初始 Q矩阵中的估计成功率。估计成功是指估计的 Q矩阵(包含基础题和新题)与真实Q矩阵完全相同。

4.2 研究结果

表1是LROE算法的估计结果, 图2、图3和图4描述了LROE算法对Q, Q和Q的成功次数变化曲线。表2列出了LROE算法在各种情况下成功估计的平均运行时间, 表3列出了LROE算法在各种情况下基于真实Q矩阵和估计矩阵Q时, 模式判准率(Leighton et al., 2004)及其变化情况。

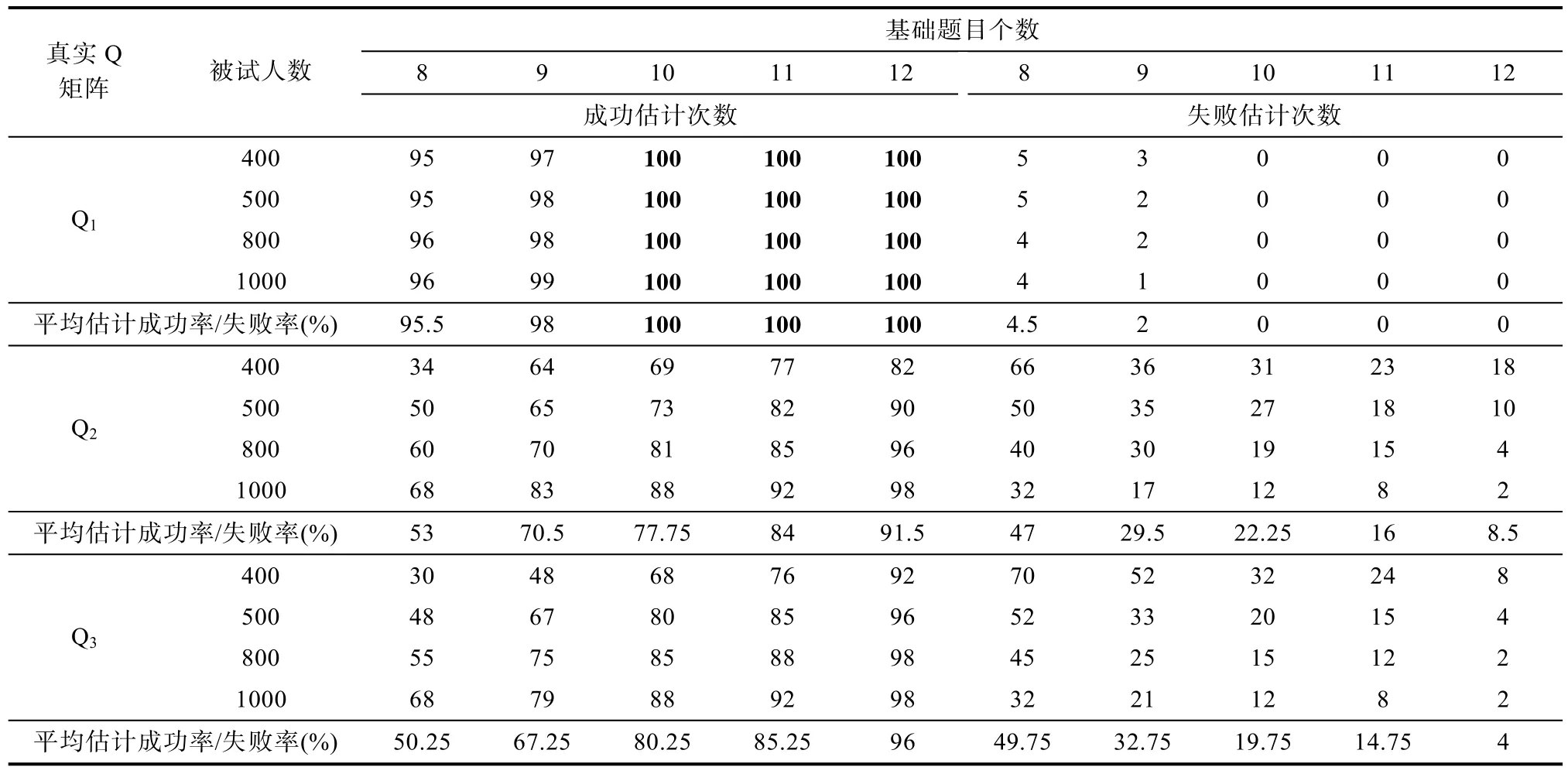
表1 使用LROE算法估计Q矩阵的结果

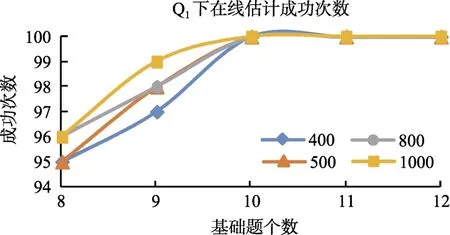
图2 LROE算法对Q1矩阵成功次数变化曲线

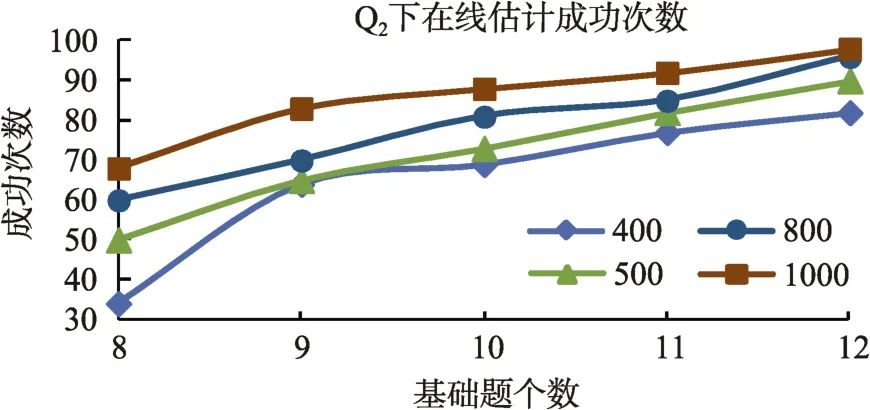
图3 LROE算法对Q2矩阵成功次数变化曲线

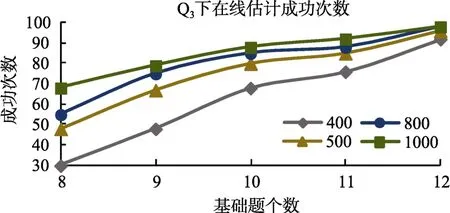
图4 LROE算法对Q3矩阵成功次数变化曲线

从表1的结果来看, LROE算法有较高的Q矩阵估计成功率, 即使是“基础题”和“被试人数”都较少时。比如, 当被试为400人, Q下, “基础题”为8个时, 估计的成功率达到95%。当“基础题”达到10个, 被试人数为400或更多, 就可以100%的恢复上述指定的正确的

Q

矩阵。对于Q和Q, 当“基础题”只有9个, 即使是人数达到1000, LROE算法的成功率也较低, 分别只有 83%和 79%, 当“基础题”增加到12个时, 估计的成功率都达到98%。这说明,当 Q矩阵中的属性个数增多时, 相对于被试人数,“基础题”的个数显得更加重要, 比如对于Q, 当被试人数为400, “基础题”从8逐渐增加到12, 成功率分别增加 18%、20%、8%和 16%, 每增加一个“基础题”, 成功率平均增加15.5%; 当“基础题”为8个,被试人数从400增加到1000, 估计成功率分别增加18%、7%和13%, 每增加100人, 成功率平均增加6.3%。

从表1中还可以看出, 当被试人数为 500或800时, “基础题”达到9个或以上时, LROE算法对Q的估计成功率低于 Q的估计成功率。直观的理解会认为在相同被试人数、相同基础题目条件下,算法对Q的估计成功率应该要高于Q的估计成功率。为什么会出现这种反常的现象？通过检查模拟程序在各次迭代的中间结果和 Q矩阵的估计值发现：在错误估计Q的情形下, 通常是由于对最后两个题目的估计不准确所导致的。不同于Q和Q, Q的最后两个题目都是考察了所有的属性(下面称“全属性题目”), 而Q中只有一个“全属性题目”, Q中没有“全属性题目”, 当真实矩阵中包含多个“全属性题目”时, 算法更容易出现错误估计的情况。

表2是使用LROE算法在100批数据中, 成功估计时的平均使用时间。这里只统计成功估计的时间, 主要是由于估计不成功时, 模拟程序达到收敛条件需要经过很多次迭代, 不同批次数据的执行时间差异较大。在LROE算法的执行过程中, 在第二步的(6)处设置最大执行次数, 在成功的估计过程中, 第二步的(6)执行次数一般都不超过 10次, 因此, 可以设置第二步的(6)执行次数达到 20次时,强制结束算法的执行。

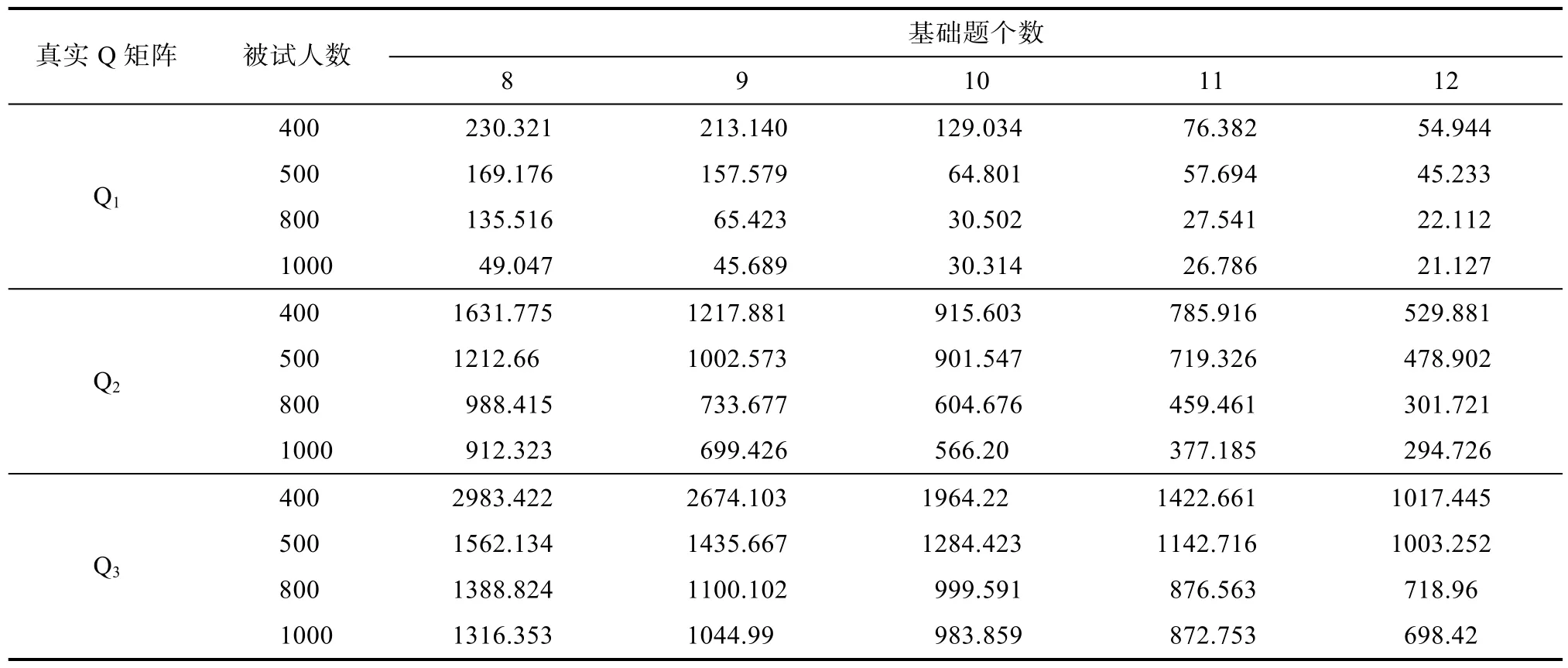
表2 使用LROE算法成功估计Q矩阵的平均执行时间(单位：秒)

从表2的结果来看, 基础题个数和被试人数共同影响着算法的执行时间。固定被试人数时, 增加基础题; 或者固定基础题, 增加被试人数都可以降低算法的运行时间。当被试人数和基础题个数都较少时, 比如400人, 8个基础题, 在三个Q矩阵下,算法都需要最多的时间, 因为此时算法成功估计需要的迭代次数较多。表2中还可以看出, 当测验中考察的属性个数增加时, 会导致算法的执行时间急剧增加, 比如三个Q矩阵, 400人, 8个基础题时的执行时间分别为：230.321秒, 1631.775秒和2983.422秒, 这是因为每增加1个属性, 会导致每个题目可能的属性向量个数翻一番。

表3是基于作答数据和LROE算法估计得到的Q矩阵, 采用DINA模型进行分析得到的平均属性掌握模式判准率。从中可以看出, 模式判准率的变化反映了LROE算法的估计成功率, 即算法的估计成功率越高, 采用Q矩阵估计值和真实Q矩阵得到的模式判准率就越接近。对于真实的Q矩阵, 无论是在 Q, Q或 Q下, 被试人数的增加与属性模式判准率之间没有必然的联系, 这一点可以从表3中的第3列数据可以看出。对于采用LROE算法估计得到的Q矩阵, 平均模式判准率会随着“基础题”的增加而增加, 这是因为增加“基础题”会提高算法的估计成功率。固定被试人数, 随着“基础题”的增加,平均模式判准率会更接近于基于真实 Q矩阵对应的模式判准率。

4.3 统计检验

为了考查Q, Q和Q下, LROE算法的估计结果在不同被试人数或“基础题”个数下是否有差异, 进行基于“被试人数”或“基础题”的单因素方差分析。

从表4的分析结果可以看出, 不论是Q, Q还是 Q, 在显著性水平为 0.05时, 不同“被试人数”(实验中涉及到的4种样本量)下的Q矩阵估计成功率之间不存在显著差异, 但是不同“基础题”个数(实验中涉及到的5种个数)下的Q矩阵估计成功率之间有显著差异, “事后多重比较”的检验结果如表5所示。

从表5中检验的结果可以看出, 在Q下, 8个“基础题”与9, 10, 11和12个“基础题”的估计成功率都有显著差异; 而9, 10, 11和12个“基础题”的估计成功率之间两两不存在显著差异。在Q下, 8个“基础题”与9, 10, 11和12个“基础题”的估计成功率也都有显著差异; 而9, 10和11个“基础题”的估计成功率之间两两不存在显著差异, 9个“基础题”与12个“基础题”的估计成功率之间有显著差异。在 Q下, 8个“基础题”与9, 10, 11和12个“基础题”的估计成功率都有显著差异; 而9与10个“基础题”的估计成功率之间没有显著差异, 9个“基础题”与11和12个“基础题”的估计成功率之间有显著差异。

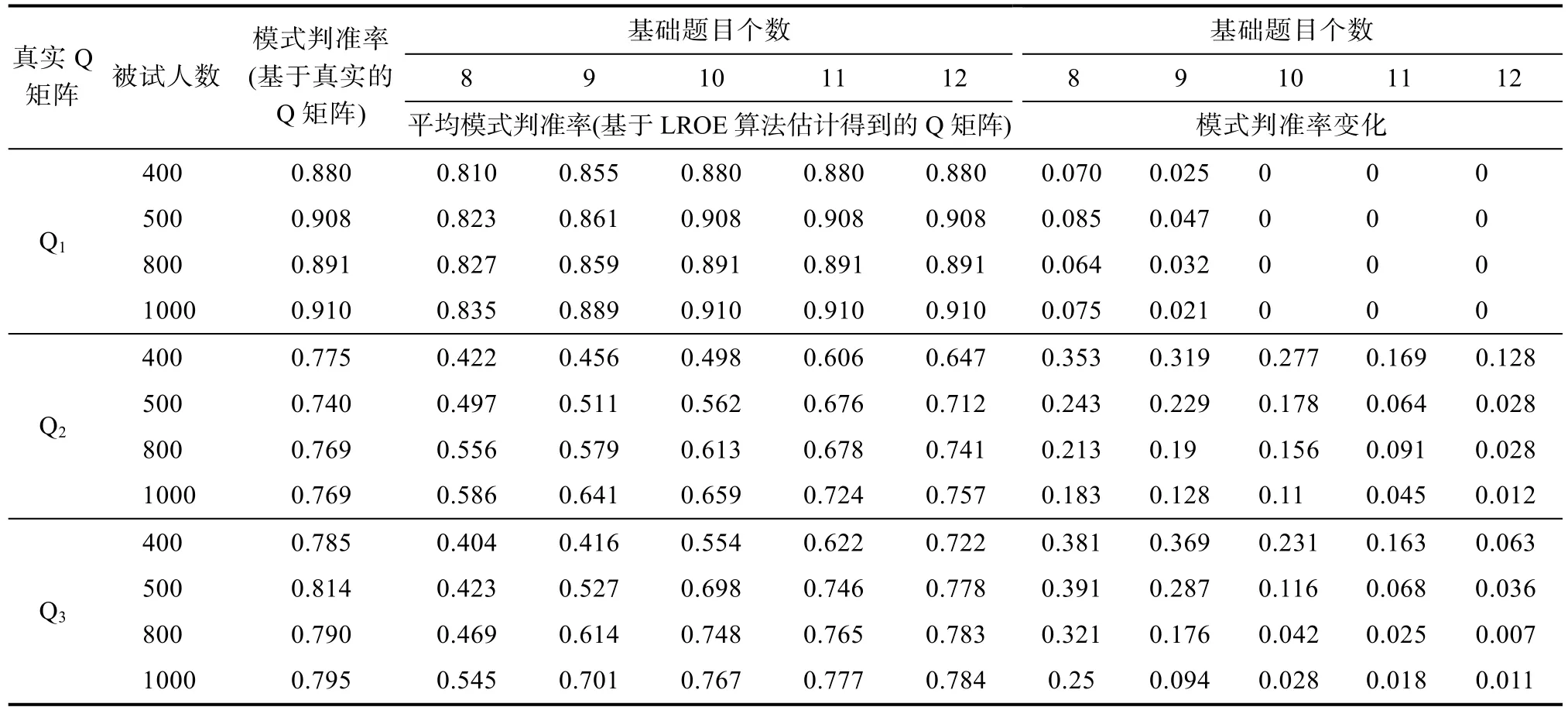
表3 基于真实和估计Q矩阵的模式判准率

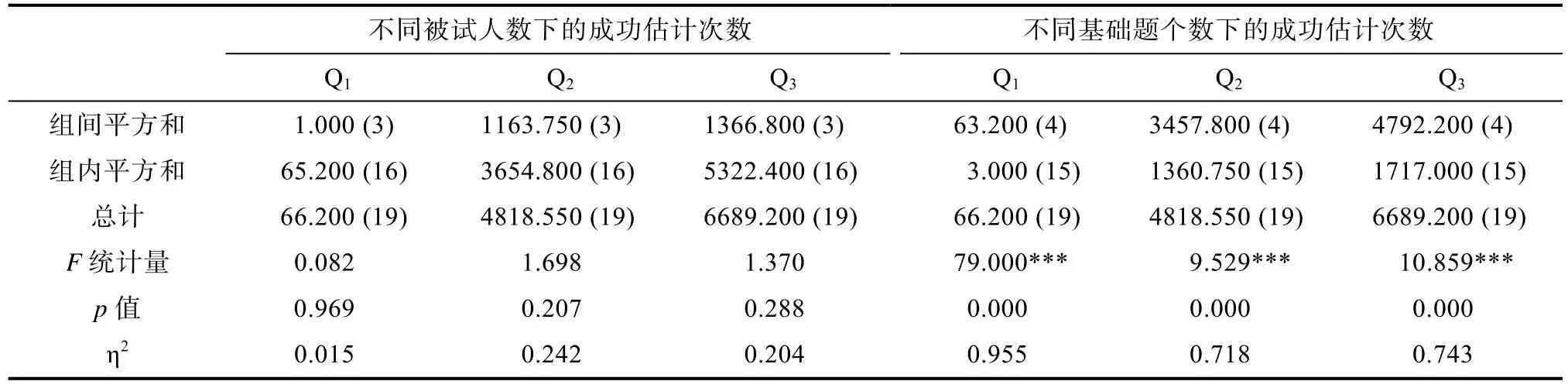
表4 LROE算法估计结果的统计检验分析

表5 Q1, Q2和Q3下, LROE算法在不同“基础题”条件下估计成功率的事后多重检验

5 总结与讨论

题目属性向量的定义对于认知诊断评价是十分重要的, 采用似然比

D

统计量对 Q矩阵进行估计, 可以基于“基础题”, 对“新题”实现在线估计,进一步对测验中的所有题目进行“校正”, 这样即使是“基础题”较少时, LROE算法都可以有较高的估计成功率。相对于本文中提到的其它题目属性定义方法, LROE算法有一些优点, 主要表现在：(1)实现了被试的属性掌握模式、题目属性向量和题目参数的在线联合估计; (2)即使当“基础题”个数较少,被试量较小时, 有较高的估计成功率; (3)更简单和省时。

D

统计量比Liu等(2011, 2012)的

S

统计量执行效率更高, 在相同的条件下(属性个数, 被试人数和题目个数都相同)下, LROE更省时, 比如, 采用 matlab 编写程序, 当人数为 1000, 属性个数为3, 20个题目中有3个错误题目, 在CPU为Intel 酷睿i7 2600, 8G内存的台式计算机上, 在成功估计时,LROE算法需要 40.059秒, 而 Liu等算法需要408.954秒, 从时间上来看, LROE算法不到Liu等算法的1/10。这是因为Liu等人的方法中涉及到

T

矩阵和β向量的计算, 即使是属性个数为 3时, 题目个数为 20,

T

矩阵和β向量的行数也是一个“巨大”的数字, 虽然Liu等对算法中

T

矩阵中的行数进行了压缩, 但是算法仍然很费时。从结果上看, 使用

D

统计量来估计题目的属性向量, 对样本量要求不高。即使是400人, 当“基础题”达到10个, 估计算法在Q上的估计成功率是100%, 这样一来, 使得本方法有很好的实用性。“在线估计算法”需要通过两步完成, 第一步是增量估计需要估计的题目, 第二步是对所有的题目进行“校正”, 从而对题目实现了“双重校正”, 可以保证“在线估计”的成功率。并且, 如果Q矩阵中只有少部分题目存在疑问或错误时, 也可以直接使用LORE算法的第二步进行被试的属性掌握模式、题目参数和题目的属性向量进行联合估计。因此,LORE算法可以较好的处理两种情况：一是专家界定的Q矩阵(作为初始的Q矩阵)质量较好, 只包含少部分错误, 可以直接使用第二步进行联合估计;二是只有少部分题目已经正确定义, 有更多的题目需要定义, 则可以使用LORE算法先进行增量式在线估计, 然后进行所有题目的整体联合估计。使用

D

统计量进行 Q矩阵估计时, 从统计检验的结果来看, 为了获得较好的估计成功率, “基础题”数量最好取8个以上。LORE算法对被试人数有一定的要求, 当被试人数少于400时, 比如200或300, 算法的估计成功率会很低。需要特别注意的是,当被试人数达到 1000甚至更多时, 算法的估计成功率并不会有明显的优势, 因此, 使用D统计量进行Q矩阵估计的理想被试人数应该是800到1000。本研究中所采用的Q矩阵相对比较简单, LORE算法对于更复杂的情况下的表现如何值得更进一步研究。

当然, 以上结果都是基于模拟数据下的结果,D统计量的在线估计算法还需要在实际测验中去验证。

Bock, R. D. (1972). Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika, 37(1), 29-51.

Chen, P., & Xin, T. (2011a). Developing on-line calibration methods for cognitive diagnostic computerized adaptive testing. Acta Psychologica Sinica, 43(7), 710-724.

[陈平, 辛涛. (2011a). 认知诊断计算机化自适应测验中在线标定方法的开发. 心理学报, 43(6), 710-724.]

Chen, P., & Xin, T. (2011b). Item replenishing in cognitive diagnostic computerized adaptive testing. Acta Psychologica Sinica, 43(7), 836-850.

[陈平, 辛涛. (2011b). 认知诊断计算机化自适应测验中的项目增补. 心理学报, 43(7), 836-850.]

de la Torre, J. (2008). An empirically based method of Q-matrix validation for the DINA model： Development and applications. Journal of Educational Measurement, 45(4),343-362.

de la Torre, J. (2009). DINA model and parameter estimation：A didactic. Journal of Educational and Behavioral Statistics, 34(1), 115-130.

DeCarlo, L. T. (2011). On the analysis of fraction subtraction data： The DINA model, classification, latent class sizes,and the Q-matrix. Applied Psychological Measurement,35(1), 8-26.

DeCarlo, L. T. (2012). Recognizing uncertainty in the Q-Matrix via a bayesian extension of the DINA model.Applied Psychological Measurement, 36(6), 447-468.

Ding, S. L., Luo, F., & Wang, W. Y. (2012). Extension to Tatsuoka’s Q matrix theory. Psychological Exploration,32(5), 417-422.

[丁树良, 罗芬, 汪文义. (2012). Q矩阵理论的扩展. 心理学探新, 32(5), 417-422.]

Ding, S. L., Mao, M. M., Luo, F., & Cui, Y. (2012). Evaluating the consistency of test items relative to the cognitive model for educational cognitive diagnosis. Acta Paychologica Sinica, 44(11), 1535-1546.

[丁树良, 毛萌萌, 汪文义, 罗芬, Cui, Y. (2012). 教育认知诊断测验与认知模型一致性的评估. 心理学报, 44(11),1535-1546.]

Ding, S. L., Wang, W. Y., & Luo, F. (2012). Q matrix and Q matrix Theory in cognitive diagnosis. Journal of Jiangxi Normal University (Natural Science), 36(5), 441-445.

[丁树良, 汪文义, 罗芬. (2012). 认知诊断中Q矩阵和Q矩阵理论. 江西师范大学学报(自然科学版), 36(5), 441-445.]

Ding, S. L., Wang, W. Y., & Yang, S. Q. (2011). The design of cognitive diagnostic test blueprints. Journal of Psychological Science, 34(2), 258-265.

[丁树良, 汪文义, 杨淑群. (2011). 认知诊断测验蓝图的设计. 心理科学, 34(2), 258-265. ]

Ding, S. L., Yang, S. Q., & Wang, W. Y. (2010). The importance of reachability matrix in constructing cognitively diagnostic testing. Journal of JiangXi Normal University (Natural Science), 34(5), 490-494.

[丁树良, 杨淑群, 汪文义. (2010). 可达矩阵在认知诊断测验编制中的重要作用. 江西师范大学学报, 34(5),490-494.]

du Toit, M. (2003). IRT from SSI: bilog-mg, multilog, parscale,testfact. Scientific Software International.

Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3), 258-272.

Leighton, J. P., Gierl, M. J., & Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment： A variation on Tatsuoka's rule-space approach. Journal of Educational Measurement, 41(3), 205-237.

Liu, J. C., Xu, G. J., & Ying, Z. L. (2011). Theory of the self-learning Q-matrix. Prepriint, 19, 1790-1817.

Liu, J. C., Xu, G. J., & Ying, Z. L. (2012). Data driven learning of Q matrix. Applied Psychological Measurement, 36(7),548-564.

McKinley, R. L., & Mills, C. N. (1985). A comparison of several goodness-of-fit statistics. Applied Psychological Measurement, 9(1), 49-57.

Orlando, M., & Thissen, D. (2000). Likelihood-based item-fit indices for dichotomous item response theory models.Applied Psychological Measurement, 24(1), 50-64.

Rupp, A. A., & Templin, J. L. (2008). The effects of Q-matrix misspecification on parameter estimates and classification accuracy in the DINA model. Educational and Psychological Measurement, 68(1), 78-96. doi： 10.1177/0013164407301545

Tatsuoka, K. K. (1983). Rule space： An approach for dealing with misconceptions based on item response theory.Journal of Educational Measurement, 20(4), 345-354.

Tatsuoka, K. (1990). Toward an integration of item-response theory and cognitive error diagnosis. In N. Frederiksen, R.Glaser, A. Lesgold, & Safto, M. (Eds.), Monitoring skills and knowledge acquisition (pp. 453-488). Hillsdale, NJ：Erlbaum.

Tu, D. B., Cai, Y., & Dai, H. Q. (2012). A new method of Q-Matrix validation based on DINA model. Acta Psychologica Sinica, 44(4), 558-568.

[涂冬波, 蔡艳, 戴海崎. (2012). 基于DINA模型的Q矩阵修正方法. 心理学报, 44(4), 558-568.]

Wang, W. Y., & Ding, S. L. (2010). Attribute identification of new items in cognitive diagnostic computerized adaptive testing. Paper presented at 9th cross-strait conference on psychological and educational testing, Taiwan.

[汪文义, 丁树良. (2010). 计算机化自适应诊断测验中原始题的属性标定. 第九届海峡两岸心理与教育测验学术研讨会, 台湾.]

Wang, W. Y., Ding, S. L., & You, X. F. (2011). On-line item attribute identification in cognitive diagnostic computerized adaptive testing. Acta Psychologica Sinica, 43(8), 964-976.

[汪文义, 丁树良, 游晓锋. (2011). 计算机化自适应诊断测验中原始题的属性标定. 心理学报, 43(8), 964-976.]

Xiang, R. (2013). Nonlinear penalized estimation of true Q-Matrix in cognitive diagnostic models. Unpublished doctorial dissertation, Columbia University.

Yen, W. M. (1981). Using simulation results to choose a latent trait model. Applied Psychological Measurement, 5(2),245-262.