基于回声状态网络的OTHR 海杂波抑制方法∗
2015-01-22张亚璇解洪文胡进峰李会勇谢菊兰
何 漫,张亚璇,解洪文,胡进峰,李会勇,谢菊兰
(1.中国运载火箭技术研究院研发中心,北京100076;2.电子科技大学电子工程学院,四川成都611731)
0 引言
OTHR中舰船等慢速海面目标的检测是当前研究难点和热点之一,受到广泛关注[1-5]。慢速目标检测的关键在于抑制海杂波从而显出目标信号。由于慢速目标回波信号靠近强大的海杂波频谱,容易被海杂波谱峰掩盖,使海杂波抑制非常困难[1-3];此外,从理论上看,长相干积累时间(Coherent Integration Time,CIT)可以提高多普勒谱分辨率,有利于慢速目标的检测。然而,实际工程中,长CIT会导致雷达探测范围和数据率降低,同时会加剧电离层的不平稳性引起的谱展宽效应,从而严重制约雷达对慢速海面目标的检测,因此,目前天波雷达多采用短CIT[4-5]。而短CIT情况下多普勒分辨率较低,使得海杂波和目标信号更加难以区分,进一步加大了抑制海杂波的难度。
目前天波雷达的海杂波抑制方法主要有海杂波对消类方法[6-7]和子空间类方法[8-10]。海杂波对消类方法包括循环对消算法及其改进算法[6-7]等。这类方法在频域上对杂波分量的参数进行估计,在时域上对信号进行处理,采用多次迭代将海杂波逐次消去,显出目标。子空间类方法包括奇异值分解(Singular Value Decomposition,SVD)的方法及其改进算法[8-9]、特征子空间(Feature Subspace,FS)法及其改进算法[10]等。此类方法利用相邻参考距离单元的海杂波的相关性来构建协方差矩阵,将其进行特征分解得到杂波子空间和信号子空间,把需要检测的目标单元的回波信号投影到信号子空间中,从而抑制海杂波,留下目标信号。
上述方法主要是利用海杂波与目标信号的时频特征不同来抑制海杂波,在目标速度较高时很有效。然而在短CIT、慢速目标情况下,目标与海杂波信号的时频特征的区分度很小,上述方法易引起目标信号发生频谱偏移,或者误将目标当成海杂波对消而降低回波的信杂噪比。前者会造成较大的目标检测误差,后者使目标淹没在海杂波中。
针对上述问题,本文注意到海杂波与目标信号有着不同的物理本质特征:天波雷达中的海杂波是一种混沌信号[11-13],而目标信号不是混沌信号。基于该思想,本文提出一种基于回声状态网络的海杂波抑制方法。该方法首先通过分析得出天波雷达海杂波具有混沌特性,然后根据海杂波与目标信号不同的动力学特征,对混沌海杂波进行重构和抑制。考虑到回声状态网络具有非常强大的非线性映射能力,本文用该神经网络重构和抑制海杂波:首先用海杂波参考信号来训练该网络,把海杂波的混沌动态特征映射到网络;在此基础上,进一步用训练好的网络重构和预测天波雷达回波中的海杂波,雷达回波减去该重构的海杂波,实现海杂波的抑制。对实测低速目标数据的处理结果表明,经本文方法后的目标信号的频谱比周围杂波频谱高了6.84 d B以上,而使用传统的循环对消法以及SVD方法后目标信号的频谱只比周围杂波频谱分别高1.53 dB和0.8 d B,因此本文方法具有更好的海杂波抑制效果。
1 回声状态网络结构模型
回声状态网络(Echo State Network,ESN)作为一种新型的递归神经网络,其隐含层是一个包含大量神经元的稀疏网络,神经元个数远远多于其他神经网络,因而具有更强大的非线性映射能力;神经元之间的稀疏连接(稀疏度为0.01~0.05)保证了网络对信号的包容性,使网络具有非常强的学习能力;同时,ESN又克服了传统神经网络结构难确定、收敛速度慢以及训练算法过于复杂等缺点,因而广泛应用于非线性信号预测、模式识别及非线性系统建模等诸多领域[14-15]。
图1是回声状态网络的结构模型,与传统神经网络模型一样,回声状态网络也由输入层、隐含层和输出层构成。但相比其他神经网络,ESN的隐含层是一个包含大量神经元的稀疏网络,具有动态特性以及短时记忆功能。隐含层中通常包含20~500个神经元,神经元之间采用稀疏连接的方式,且连接权Wres随机产生。输入信号u(n)通过输入连接权Win与隐含层连接,输入节点为K,输出信号y(n)通过反馈连接权Wfb反馈给隐含层,输入信号、隐含层的内部状态以及输出信号的上一状态共同通过输出连接权Wout连接至输出层。隐含层的内部状态更新方程为
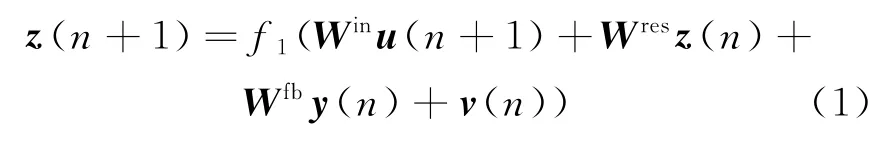
式中,z(n)为隐含层的内部状态向量,v(n)为维持网络稳定的噪声向量,f1为sigmoid函数,记为

输出方程为

式中,f2取恒等函数,这样输出节点是线性的。
2 本文所提海杂波抑制方法
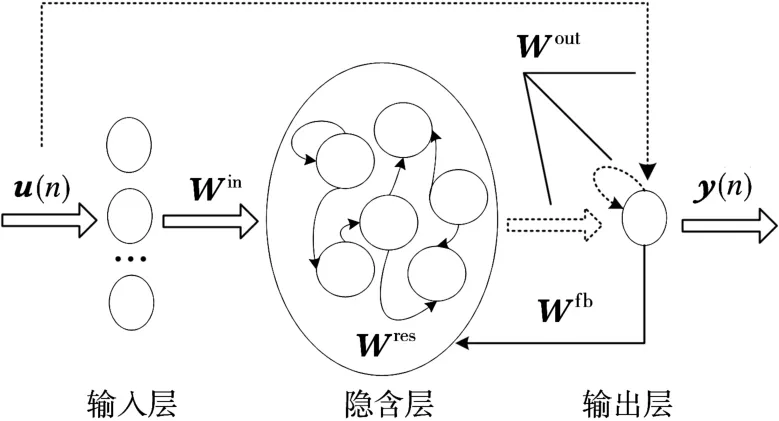
图1 回声状态网络结构模型
传统的海杂波抑制方法基本上都是从海杂波与目标信号的时频特征的不同来区分这两类信号,从而达到抑制海杂波的目的。在高速目标情况下,这些方法能取得很好的效果;对于短CIT情况下的低速目标,这种区分度其实很小,造成海杂波抑制效果不理想。
本文直接从海杂波和目标信号不同动力学特征的角度来对两类信号进行区分,具有更大的区分度。所以,在短CIT、低速目标情况下,本文方法对海杂波具有更好的抑制效果。
本节首先计算天波雷达海杂波的相空间参数,并通过分析证明海杂波是一种混沌信号,在此基础上,进一步提出使用回声状态网络来对混沌海杂波进行重构和抑制。首先用回声状态网络获得海杂波的内在动力学特征;然后根据杂波信号和目标信号的动力学特征不同,继续使用回声状态网络对回波信号中的杂波成分进行重构和对消,实现天波雷达海杂波抑制。
2.1 海杂波混沌性质分析
传统的天波雷达海杂波建模中,通常把海杂波近似成正弦信号叠加[1-5]。本节则首先研究天波雷达海杂波信号的物理特征,在此基础上,将天波雷达海杂波建模成混沌信号,从而找出海杂波与目标信号在物理本质特征上的不同。
下面首先计算海杂波信号的相空间重构参数,通过嵌入维数中稳定性判断准则判断得出天波雷达海杂波信号是一种确定信号;然后进一步计算其最大Lyapunov指数,最大Lyapunov指数为正表明海杂波信号是一种混沌信号。
2.1.1 海杂波的相空间参数
本节将一组不含目标信息的天波雷达回波作为参考单元来重构海杂波的原始动力系统,即对于海杂波序列{x(i),i=1,2,…,N},利用延迟时间τ构造K维相空间矢量:
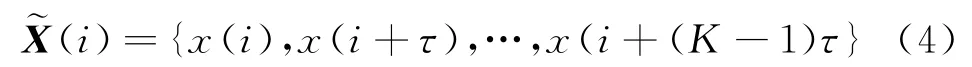
这里使用Cao氏法计算嵌入维数。计算过程如下:
首先计算海杂波K维相空间与K+1维相空间最近邻点距离比值:

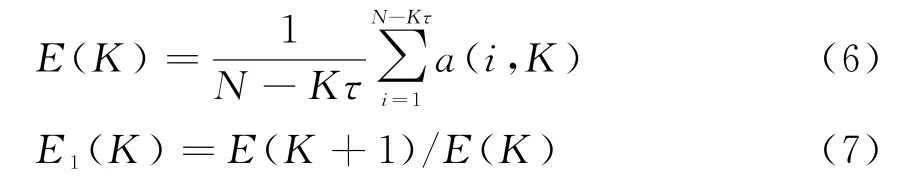
对于一个确定时间序列,存在某个K0,使E1(K)的值在K>K0后不再变化,此时K0+1就是所求的最小嵌入维数。由于天波雷达海杂波数据是有限长序列,很难判断E1(K)是在缓慢变化还是趋于稳定,故补充判断准则:

对于随机序列,数据间没有关联性,所以无论K如何变化,E2(K)≡1。而对于确定序列,数据间的相关性随嵌入维数K的变化而变化,故总存在K,使E2(K)≠1。通过所求E2(K)的值可以判断海杂波信号确实是一种确定序列,不是随机序列。
2.1.2 海杂波的最大Lyapunov指数
上述计算说明了天波雷达海杂波信号是一种确定信号,确定信号又分为混沌信号和非混沌信号。下面通过最大Lyapunov指数进一步验证海杂波信号是一种混沌信号。
系统的Lyapunov指数反映了相空间中两个相邻轨迹之间的收敛和发散率,如果系统中至少有一个Lyapunov指数为正,则系统具有混沌特性[16]。
这里使用所需数据量较小以及计算复杂度低的Rosenstein小数据量法[17]计算天波雷达海杂波信号的最大Lyapunov指数,具体计算过程如下:
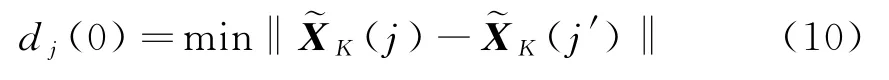
式中,|j-j′|>p,p为海杂波信号的平均周期。于是,海杂波信号的最大Lyapunov指数的计算式为
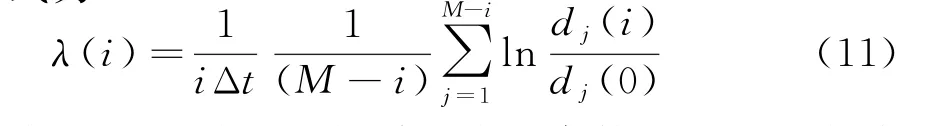
式中,i为相点j沿轨道的步长序数,Δt为海杂波信号样本周期,M为对海杂波进行相空间重构的相点的个数,dj(i)有如下近似关系:

对式(12)两边取对数,得
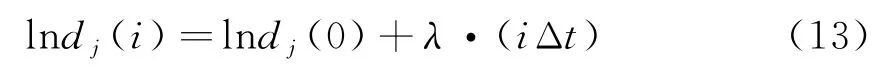
通过对式(13)的斜率进行最小二乘逼近即可求得海杂波的最大Lyapunov指数,即

式中,<·>表示按相空间点j求平均。
根据上述方法,可计算出海杂波的最大Lyapunov指数大于零,这就证明了天波雷达海杂波信号是一种天然的混沌信号。
2.2 基于混沌海杂波重构的杂波抑制
上节的分析表明,天波雷达海杂波是一种混沌信号,而混沌信号在短时间内是可以精确预测的。本文根据海杂波和目标不同的动力学特征,提出一种基于回声状态网络的天波雷达杂波抑制方法。
该方法包括两个阶段:海杂波混沌特征提取阶段以及海杂波预测和对消阶段。在海杂波混沌特征提取阶段,使用一组不包含目标信息的海杂波参考信号训练回声状态网络,使网络“记住”海杂波内部的动力学特征;在海杂波预测和对消阶段,用前述训练好的网络,对需要检测目标单元的回波信号中的海杂波进行一步预测。由于回波信号中杂波和目标的动力学特征不同,而回声状态网络只记住了杂波的动力学特性,因此只能有效预测杂波,但不能有效预测目标信号,这样目标信号成为预测误差中的主要成分,从而实现海杂波抑制。
2.2.1 海杂波混沌特征提取
本文将一段海杂波参考信号作为输入信号样本训练ESN系统获得海杂波的内在动力学特征。通常该参考信号是复信号,需要对信号的实部和虚部(I、Q通道)分别进行训练来提取其混沌特征。这里以I通道的训练为例。
如图2所示,用于训练的海杂波I通道数据为{ur(n),n=1,2,…,M},其中M为海杂波样本个数;在n时刻回声状态网络的输入向量ur(n)记为

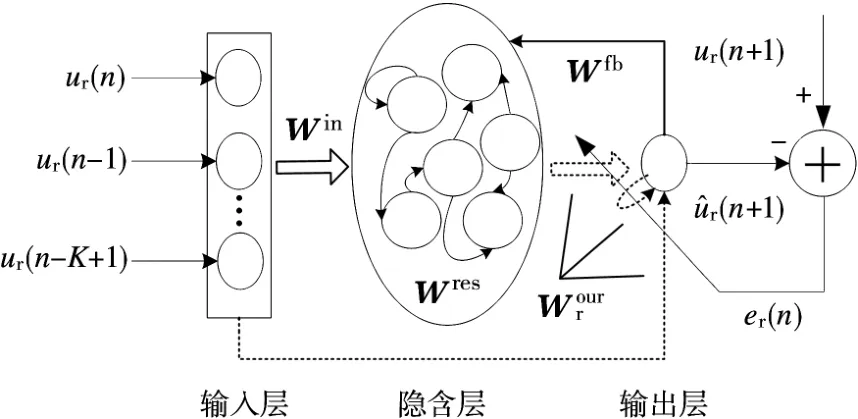
图2 海杂波混沌特征提取的示意图
神经元的内部状态向量完全反映了天波雷达海杂波信号的演化规律,在对ESN网络训练过程中,需要不断更新隐含层内部神经元的状态向量,使ESN“记住”海杂波内部的混沌特征。这里内部神经元的初始状态zr(0)=0。神经元状态更新方程可以表示为

式中:z(n)为神经元的内部状态向量;v(n)为维持网络稳定的噪声向量;Win,Wres和Wfb分别为回声状态网络的输入连接权值矩阵、神经元内部连接权值矩阵和反馈连接权值矩阵,这三个权值矩阵经初始随机生成后便不再改变。
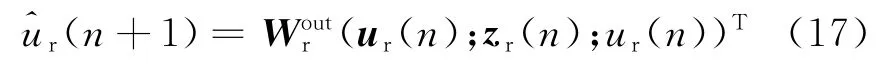
在求出zr(n)后,通过如下输出方程得到最优输出权值矩阵Woutr:该式是一个线性方程,其最优权值可以使用最小均方(LMS)算法和递归最小二乘(RLS)算法等线性自适应算法求得。相比其他采用非线性方程求解最优权值的神经网络而言,大大简化了计算的复杂程度,提高了运算速度和权值收敛率。
2.2.2 海杂波预测和对消
回声状态网络提取海杂波的混沌特征后,用其对海杂波进行预测和对消。在该阶段,回声状态网络的状态更新函数以及输出函数与海杂波特征提取阶段保持一致,且网络中的各个参数不再变化,此时ESN系统相当于一个内部封闭的系统。
海杂波预测和对消过程如图3所示,图中以I通道数据ur(n)为例,将需要检测目标单元的回波信号作为ESN的输入信号,当通过经海杂波训练后的ESN系统时,系统输出的信号是的一步预测信号。即在n时刻,输入向量为


图3 海杂波预测和对消示意图
Q通道预测误差~ei(n)的求解与I通道相同,在求得两个通道的预测误差序列后可求出总的预测误差序列:
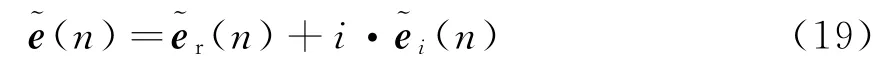
3 仿真结果分析
仿真采用某天波雷达的实测数据,其部分参数如下:天波雷达工作频率f0=14.34 M Hz,采样脉冲数M=512,脉冲周期T=12 ms,相干积累时间CIT=6.14 s。
首先通过仿真计算出天波雷达海杂波的嵌入维数,并证明海杂波信号是一种确定信号,然后计算其最大Lyapunov指数进一步证明海杂波是一种混沌信号。在此基础上,用回声状态网络提取海杂波的混沌动力特性,然后根据目标信号与海杂波的动力学特征不同,将输入信号与回声状态网络输出的杂波预测值相减,从而显出回波信号中的低速目标。实验结果验证了本文方法的有效性以及与其他传统方法相比的优越性。
3.1 海杂波混沌性质分析
3.1.1 海杂波相空间参数
图4是用2.1.1节的算法对某距离单元的实测海杂波的嵌入维数的计算结果。图中,4条曲线分别是I通道的E1和E2曲线以及Q通道的E1和E2曲线。从图中看出,I通道和Q通道的E2都不是一条恒等于1的曲线,而是在1附近上下波动,由此得出天波雷达海杂波不是一个完全的随机信号,而是包含很多确定特征的确定信号;同时,I通道和Q通道的E1都在K=7之后基本保持不变,因此得出所求天波雷达海杂波的嵌入维数为7。
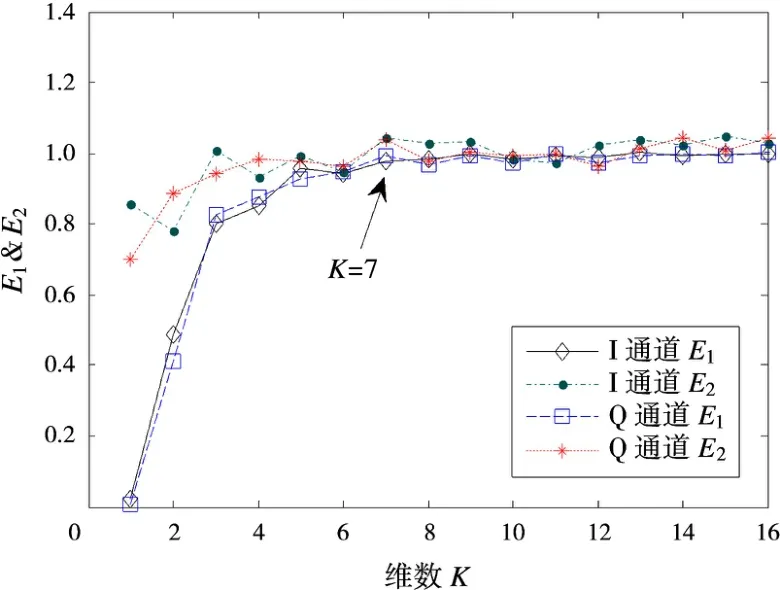
图4 Cao氏法求最小嵌入维数
3.1.2 最大Lyapunov指数的计算
这里用上述仿真得出的嵌入维数进一步计算海杂波的Lyapunov指数。仿真使用与上节同样的海杂波数据,序列的平均周期通过计算海杂波能量光谱平均频率的倒数获得。
图5是用2.1.2节小数据量法求最大Lyapunov指数的计算结果。从图中可以看出,I通道和Q通道的平均分离率

图5 小数据量法求最大Lyapunov指数
3.2 回声状态网络的海杂波抑制过程
3.1节的仿真分析表明天波雷达海杂波具有混沌特性。下面利用回声状态网络提取海杂波的混沌动力特性,实现海杂波抑制。
仿真选取两组相邻的实测海杂波信号:一组作为参考信号训练回声状态网络;另一组中添加一个舰船目标作为待检测目标单元的回波信号。仿真时先初始化回声状态网络中各个参数,取内部神经元个数N为80,随机产生一个连接率为0.03、谱半径为0.9的系数矩阵Wres,矩阵Win和Wfb的权值服从(-1,1)的均匀分布。
3.2.1 海杂波特征提取阶段的预测性能分析
这里使用一组实测海杂波参考信号训练回声状态网络。以I通道海杂波数据为例,仿真结果如图6所示。图6(a)是输入信号与回声状态网络的预测输出信号曲线图,从图上看两条曲线基本重合。继续对其预测误差进行分析,将两信号相减后得到图6(b)的预测均方误差曲线图,图中预测均方误差一直很小,即使在采样点为220~228处信号变化比较剧烈的地方,预测均方误差也在0.074以下。表明回声状态网络对天波雷达海杂波信号具有很好的预测性能。
3.2.2 海杂波预测和对消阶段杂波抑制性能分析
实测数据中没有低速舰船目标,因此本文在与上节临近的一组海杂波距离单元内添加一个速度v=15 m/s的舰船目标,目标对应的多普勒频率fd=1.0 Hz。由此得到的天波雷达回波谱如图7所示。从图中看出,海杂波能量占整个信号的主体部分,且主要分布在低频区域,而舰船目标的多普勒频率已经非常接近海杂波谱,使目标很难在强大的海杂波频谱中分离出来。

图6 I通道海杂波数据的预测结果
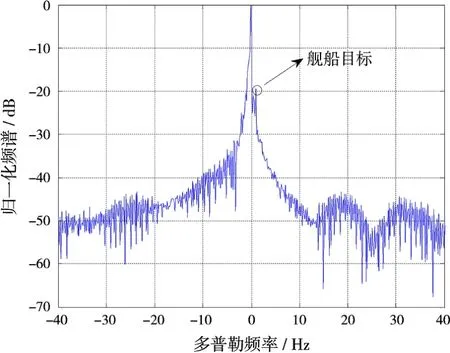
图7 天波雷达回波谱
图8(a)为式(17)得到的总的预测误差序列的频谱图。图中预测误差序列的频谱在有舰船目标的地方明显高于其他地方,表明输入信号中的杂波成分得到良好的抑制。后续工作只需设置合适的检测门限即可得出舰船目标的信息。图8(b)为经文献[6]所提循环对消法抑制海杂波后的频谱图。本仿真试验中,海杂波对消迭代次数取29次,获得该方法的最佳效果。从图上看,虽然舰船目标频谱在整个频谱轴上最高,但效果并不明显,目标谱线周围仍有很强的杂波残留,后续对舰船目标的检测仍然十分困难。图8(c)为经文献[8]所提SVD算法的目标回波频谱图。本仿真试验中去掉两个最大奇异值能得到最佳的海杂波抑制效果。由图看出,舰船目标基本淹没在残留的杂波中,使目标信号与杂波难以区分。

图8 几种海杂波抑制方法比较结果
为了进一步比较上述几种海杂波抑制方法的处理结果,将图8分别进行局部放大,得到的结果如图9所示。从图中看出,使用传统的循环对消法以及SVD方法后,舰船目标周围仍然有很强的杂波残留,目标信号的频谱只比周围杂波频谱分别高1.53 dB和0.8 dB,检测起来非常困难。而使用本文方法后,目标信号的频谱比周围杂波频谱高了6.84 dB以上,从图中看出目标信号在频谱中出现一个很高的尖峰,容易从杂波中识别出来,这就证明了本文方法对实测数据低速目标中的海杂波具有更好的抑制效果。
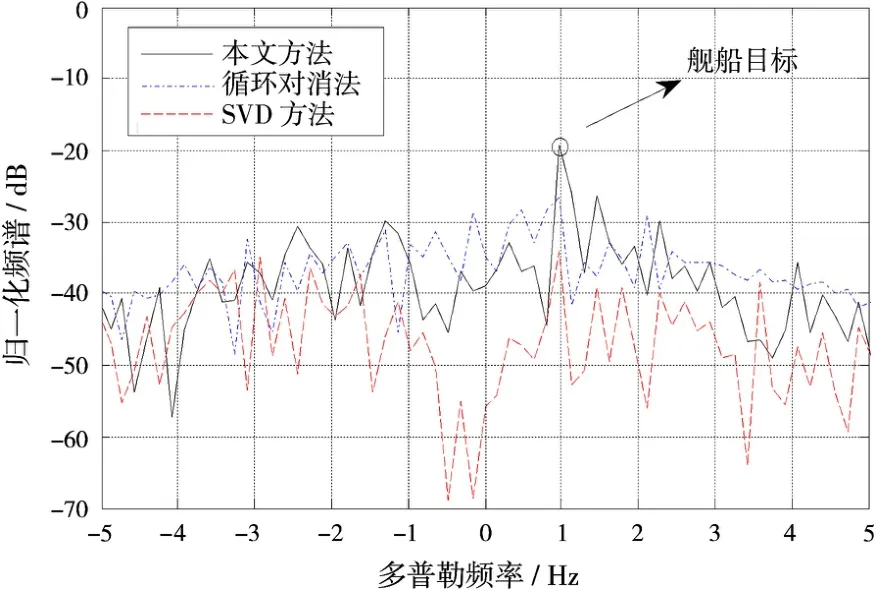
图9 几种海杂波抑制方法比较的局部放大图
4 结束语
考虑到海杂波与目标信号具有不同的动力学特征,本文提出一种基于回声状态网络的天波雷达海杂波抑制方法。该方法首先用海杂波参考信号训练回声状态网络,使该神经网络“记住”海杂波的混沌动态特征;然后用前述训练好的网络重构和预测天波雷达回波中的海杂波,雷达回波减去该重构的海杂波,实现海杂波的抑制。实测数据处理结果证明了与传统的循环对消法以及SVD方法相比,本文方法在短CIT和低速目标情况下,具有更好的海杂波抑制效果。
[1]FABRIZIO G A.High Frequency Over-the-Horizon Radar[M].NY,USA:McGraw-Hill,2013.
[2]李万阁,胡进峰,李强,等.OTHR低信噪比下的机动目标检测算法[J].雷达科学与技术,2014,12(4):373-378.LI Wan-ge,HU Jin-feng,LI Qiang,et al.Maneu-vering Target Detection Algorithm with Low Signal-to-Noise Ratio in OT H Radar[J].Radar Science and Technology,2014,12(4):373-378.(in Chinese)
[3]游伟,何子述,胡进峰.基于匹配场处理的天波雷达高度估计算法[J].电子与信息学报,2013,35(2):401-405.
[4]胡进峰,艾慧,李强,等.基于连接层的天波雷达高度估计算法研究[J].雷达科学与技术,2014,12(4):343-349.HU Jin-feng,AI Hui,LI Qiang,et al.Skywave Radar Altitude Estimation Algorithm Based on Joining Layer Model[J].Radar Science and Technology,2014,12(4):343-349.(in Chinese)
[5]SAVERINO A L,CAPRIA A,BERIZZI F,et al.Frequency Management in HF-OTH Skywave Radar:Ionospheric Propagation Channel Representation[J].Progress In Electromagnetics Research B,2013,50(1):97-111.
[6]ROOT B T.HF-Over-the-Horizon Radar Ship Detection with Short Dwells Using Clutter Cancellation[J].Radio Science,1998,33(4):1095-1111.
[7]CANDAN C.Analysis and Further Improvement of Fine Resolution Frequency Estimation Method from Three DFT Samples[J].IEEE Signal Processing Letters,2013,20(9):913-916.
[8]KHAN R H,LE-NGOC S.A Singular Value Decomposition(SVD)Based Method for Suppressing Ocean Clutter in High Frequency Radar[J].IEEE Trans on Signal Processing,1993,41(3):1421-1425.
[9]薄超,顾红,苏卫民.基于高阶奇异值分解的OTHR海杂波抑制算法[J].系统工程与电子技术,2014,36(5):872-878.
[10]WANG G,XIA X,ROOT B T,et al.Moving Target Detection in Over-the-Horizon Radar Using Adaptive Chirplet Transform[J].Radio Science,2003,38(4):1-24.
[11]盛文,任吉.天波超视距雷达海杂波的混沌动态特性分析[J].电波科学学报,2012,27(2):350-358.
[12]董华春,宗成阁,权太范.高频雷达海洋回波信号的混沌特性研究[J].电子学报,2000,28(3):25-28.DONG Hua-chun,ZONG Cheng-ge,QUAN Taifan.Chaotic Characteristics in HF Radar Backscatter from the Ocean Surface[J].Acta Electronica Sinica,2000,28(3):25-28.(in Chinese)
[13]刘建厂.混沌理论在海杂波研究中的应用[J].雷达科学与技术,2004,2(4):206-210.LIU Jian-chang.Application of Chaos Theory to Sea Clutter Research[J].Radar Science and Technology,2004,2(4):206-210.(in Chinese)
[14]宋彤,李菡.基于小波回声状态网络的混沌时间序列预测[J].物理学报,2012,61(8):90-96.
[15]JAEGER H,HAAS H.Harnessing Nonlinearity:Predicting Chaotic Systems and Saving Energy in Wireless Communication[J].Science,2004,304(5667):78-80.
[16]徐红梅,郭树旭.基于符号相对熵的Logistic混沌系统时间不可逆性分析[J].电子与信息学报,2014,36(5):1242-1296.
[17]ROSENSTEIN M T,COLLINS J J,DE LUCA C J.A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets[J].Physica D,1993,65(12):117-134.
