压缩感知在波达方向估计中的应用∗

史雪辉,朱 伟,郑 禹

(1.中国人民解放军海军驻合肥地区军事代表室,安徽合肥230088;2.中国电子科技集团公司第三十八研究所,安徽合肥230088;3.安徽建筑大学,安徽合肥230601)

0 引言

压缩感知(Compressed Sensing,CS)理论[1]与Nyquist采样定理不同,它指出只要信号是可压缩的或在某个变换域是稀疏的,那么就可以用一个与变换基不相关的观测矩阵将高维信号投影到一个低维空间上,将信号的采样变成信息的采样,然后通过求解一个优化问题就可以从这些少量的投影中高概率重构出原信号,可以证明这样的投影包含重构信号的足够信息。在CS理论框架下,采样速率不决定于信号的带宽,而决定于信息在信号中的结构和内容[2],突破了Nyquist采样定理的限制,为信号的采集和处理提供了新的思路。

实际中,被测目标在空域内是稀疏的,因此可以将目标DOA估计问题看成是一个稀疏向量的重构问题,该稀疏向量中非零元素的位置信息表征目标的角度信息,即空间谱是稀疏的。随着压缩感知理论的逐渐发展,其在阵列DOA估计领域中的应用也开始崭露头角。文献[3]将稀疏分析引入到阵列DOA估计中,通过对空间角度的离散化建立稀疏重构模型,然后使用二阶锥规划求解优化问题;文献[4]采用空域稀疏的概念,提出l-1 SVD算法,能直接应用于相干源的DOA估计,但在其优化问题求解过程中,最优正则化参数的选取仍需要进一步研究;文献[5]提出的高分辨DOA估计算法,在一定程度上也受正则化参数选取的困扰;文献[6]利用多个时刻的阵元接收数据的随机投影重构一个稀疏的角空间场景,给出信源数及其DOA,在低信噪比情况下无法适用;文献[7]提出一种压缩采样阵列,能有效降低硬件规模,采用多测量矢量欠定系统聚焦求解(MFOCUSS)算法实现DOA估计,但该算法在快拍数较多时运算复杂度较高,在低信噪比情况下估计性能较差;文献[8]在压缩采样阵列的基础上,提出一种基于奇异值分解的压缩采样阵列DOA估计算法,利用阵列结构建立过完备原子库,对接收数据矩阵进行奇异值分解,最后将信号子空间分解到最佳基向量上,实现空域信号DOA的高分辨估计,但要求阵元数较多。

针对以上问题,本文提出基于协方差矩阵CS、阵列内插CS和波束空间CS的DOA估计算法,利用目标在空域的稀疏性,分别在协方差矩阵、虚拟内插阵和波束空间上进行压缩采样,构建出新的DOA估计压缩感知模型,通过稀疏重建算法来进行信号重构,得到目标的高分辨DOA估计。最后给出计算机仿真结果。

1 基于压缩感知的DOA估计模型

考虑K个远场窄带信号入射到M个各向同性阵元组成的均匀线阵,信源个数已知,且M＞K,阵元间距为d,信号入射角为θi(i=1,2,…,K),则阵列在t时刻的接收信号为

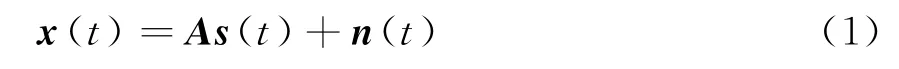
式中:x为M×1维的阵元接收数据;n为M×1维的白噪声,满足零均值、方差为σ2的复高斯分布,各阵元输出噪声统计独立;s=[s1,s2,…,sK]T为K×1维的信号矢量;A为M×K维阵列流型:

式中,a(θi)=[1,a(θi),…,aM-1(θi)]T为第i个信源的导向矢量,a(θi)=ex p(-j2πd sin(θi)/λ,λ为入射信号的波长。

信源是空域稀疏的,采用某种空间网格划分可以实现其稀疏性表示。将需要考虑的空间划分为{θ1,θ2,…,θN},假设每个θn(n=1,2,…,N)都对应一个潜在的信源sn。为了体现信源的空域稀疏性,N≫K,这样就构造一个N×1维的空域稀疏信号S=[s1,s2,…,sN]T,在S中只有实际存在目标的K个位置有非零元素,其他N-K个位置均为零。因此,式(2)可以写为

式中,Ψ为信号稀疏化表示以后对应M×N维阵列流型,也被称为超完备冗余字典。显然,x和S是等价的。

通过求解如下1范数优化问题,就可以对式(3)进行信号重构:

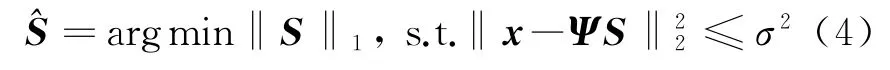
CS理论指出,把阵列的量测信号x投影到另一个与Ψ不相关的L×M(L≪M)维观测矩阵Φ上,即用观测矩阵Φ对x进行线性变换,得到L×1维的观测信号y,从而实现对x的空域压缩采样[9](Spatial CS,S-CS):

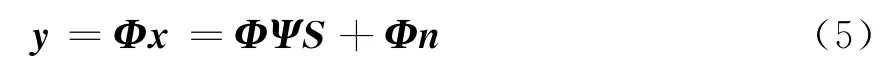
通过求解如下最优化问题可以从观测信号y中高概率地重构信号矢量S:

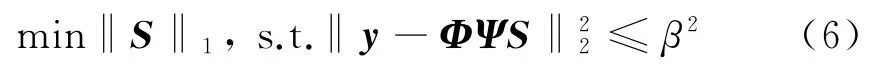
式中,β为噪声标准差。同时CS理论指出信号稀疏性越强(K越小,即信源个数越少),重构误差越小[10]。

常用的重构算法可以分为如下几类:

1)贪婪追踪算法:这类方法是通过每次迭代时选择一个局部最优解来逐步逼近原始信号。这些算法包括正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[11]等。

2)凸松弛法:这类方法通过将非凸问题转化为凸问题求解找到信号的逼近,如内点法[12]等。

3)组合算法:这类方法要求信号的采样支持通过分组测试快速重建,如链式追踪[13]等。

但是每种算法都有其固有的缺点。凸松弛法重构信号所需的观测次数最少,但往往计算量较大。贪婪追踪算法在运行时间和效率上都位于另两类算法之间。

2 压缩感知在DOA估计中的应用

实际中,大部分阵列都为均匀布阵,而且受阵列大小限制,阵列的量测信号x维数有限,相应对x进行压缩采样得到的观测信号y维数过小,利用y进行稀疏重构得到的信号S误差较大,因此S-CS算法在DOA估计中性能较差。

2.1 协方差矩阵CS算法

量测信号x的维数为M,其协方差矩阵的维数为M×M,对协方差矩阵进行压缩采样可以获得维数较大的观测信号y,再进行稀疏重构,称为协方差矩阵CS算法[14](Covariance Matrix CS,CM-CS)。

阵列量测信号矢量x的协方差矩阵R为

式中,RS为信源协方差矩阵,σ2n为噪声功率。当各信源不相关时,RS为实值对角阵。

对式(7)矩阵矢量化得到

式中,Rv=vec(R),Ψv=[av(～θ1),av(～θ2),…,N),Sv=diag(RS),Sv和S包含相同的空域信息,Iv=vec(I)。

Rv为M2×1维矢量,用L×M2(L≪M2)维观测矩阵ΦC对Rv进行压缩采样,得到L×1维的观测信号y:

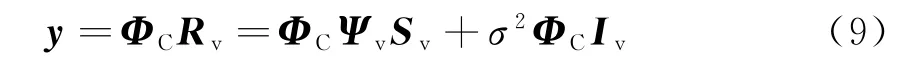
因此,式(6)的优化问题转换为

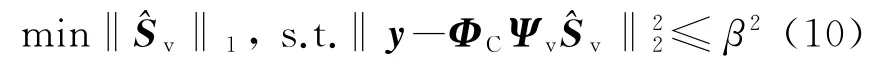
从以上公式推导中可以看出,只有在信源不相干时,RS才为实值对角阵,针对相干信源问题,提出以下的阵列内插CS算法和波束空间CS算法。

2.2 阵列内插CS算法

通过对M个阵元进行阵列内插,得到阵元为Q(Q≫M)的虚拟阵列,从而提高阵列量测信号的维数,然后对虚拟阵列的量测信号进行压缩采样,获得的观测信号y维数较大,再进行稀疏重构,称为阵列内插CS(Interpolated Arrays CS,IA-CS)算法。

假设信源位于空域Θ内,将空域Θ划分为P(P≫M)份:

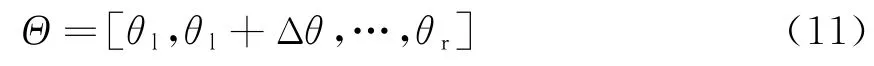
式中,θl,θr为Θ的左右边界,Δθ为步长。则在空域Θ内,真实阵列的阵列流型矩阵为

在同一空域Θ内,通过阵列内插后到的虚拟阵列的阵列流型矩阵为

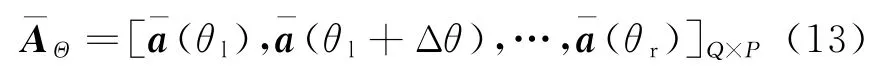
因此,内插变换矩阵BI为

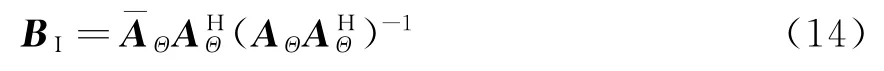
在考虑噪声的情况下得到内插变换矩阵BI为

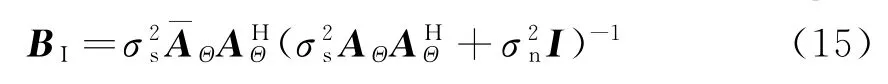
对内插变换矩阵BI进行预白化处理,得到白化内插变换矩阵TI:

通过阵列内插得到的虚拟阵列的量测信号为

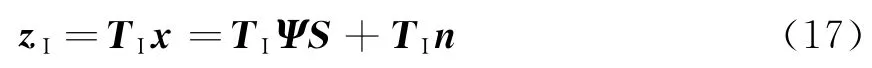
zI为Q×1维矢量,用L×Q(L≪Q)维观测矩阵ΦI对zI进行压缩采样,得到L×1维的观测信号y:

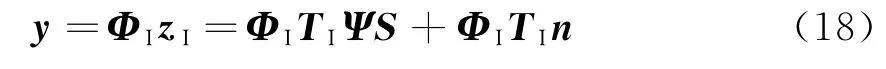
因此,式(6)的优化问题转换为

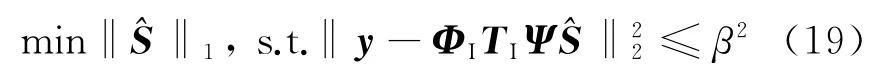
2.3 波束空间CS算法

S-CS算法、CM-CS算法和IA-CS算法都是建立在阵元域,即每个阵元都对应一个数据通道,可以先将阵列的量测信号矢量x变换至波束域,然后对波束域的量测信号进行压缩采样,再进行稀疏重构,称为波束空间CS(Beam Space CS,BS-CS)算法。

假设信源位于空域Θ内,空域Θ的定义如式(11),在空域Θ内进行波束形成得到P个波束,波束变换矩阵BB为

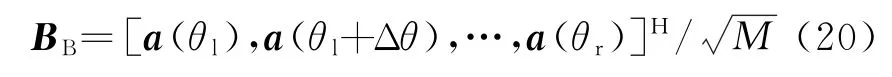
对波束变换矩阵BB进行预白化处理,得到白化波束变换矩阵TB:

通过波束变换后得到的波束域量测信号为

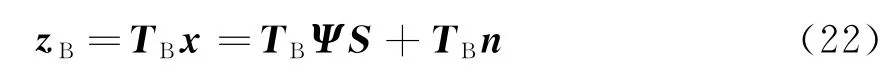
zB为P×1维矢量,用L×P(L≪P)维观测矩阵ΦB对zB进行压缩采样,得到L×1维的观测信号y:

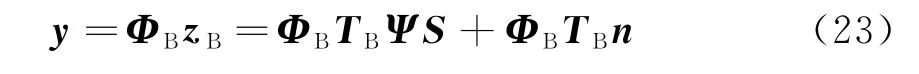
因此,式(6)的优化问题转换为

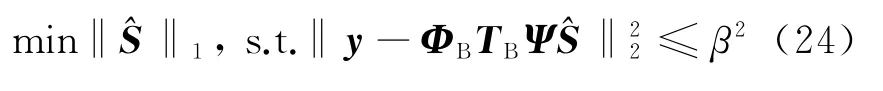
3 计算机仿真

仿真过程中,针对垂直布置的20个水平极化天线阵元组成的等距布阵,阵元间距半波长,雷达架高20 m,地面反射系数为-0.95,载波频率为300 MHz,只考虑镜面反射。将前后向空间平滑MUSIC算法[15](SS-MUSIC)、交替投影最大似然[16](AP-ML)、多测量矢量欠定系统聚焦求解算法[17](FOCUSS)和空域压缩采样[9](S-CS)与协方差矩阵CS算法、阵列内插CS算法和波束空间CS算法进行性能比较。SS-MUSIC算法中空间平滑次数为2次,FOCUSS算法中正则化系数p=0.8。搜索的空域间隔为0.01°。空域Θ定义为[-10°,-9.9°,…,10°],间隔0.1°。S-CS算法中L=4。IA-CS算法中在每两个阵元中内插9个虚拟阵元,得到的内插阵的总阵元数为Q=191。BS-CS算法中的波束数P=200。IA-CS算法和BS-CS算法中L=20。最优化问题采用OMP算法进行求解。

仿真一:不考虑多径反射时的DOA估计性能随信噪比的变化

仿真条件:单个目标,目标入射角为10°,阵元信噪比从-10 dB变化至20 dB,快拍数为20。500次Monte-Carlo实验统计的DOA估计均方根误差如图1所示。从图1可以看出,在不考虑多径反射时,针对单个目标,3种基于压缩感知的DOA估计算法性能比较接近,略优于常规MUSIC算法。

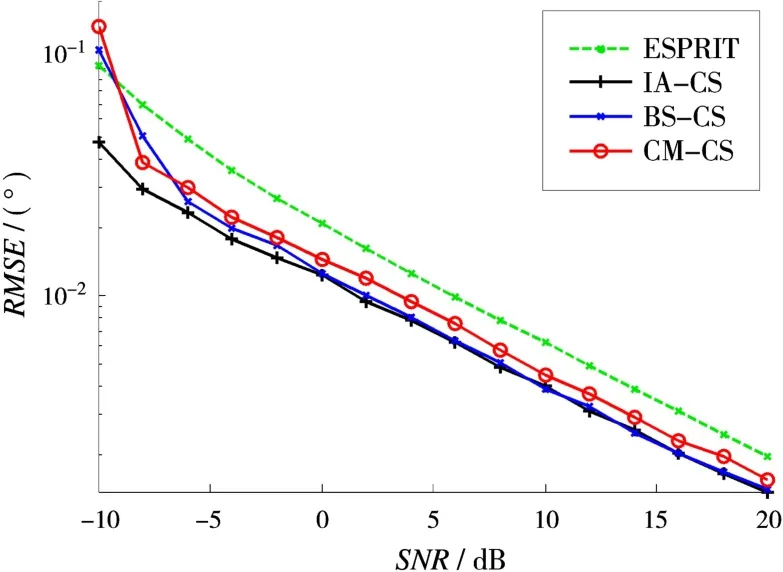
图1 仿真一信噪比变化时的性能曲线

仿真二:考虑多径反射时的DOA估计性能随信噪比的变化

仿真条件:单个目标,目标与参考天线的距离为200 km,目标直达角为2°,多径反射角为-2.01°,阵元信噪比从-10 d B变化至20 d B,快拍数为20。500次Monte-Carlo实验统计的DOA估计均方根误差如图2所示。

从图2可以看出,在考虑多径反射时,IA-CS算法和BS-CS算法的信噪比门限大于其他算法的信噪比门限。随着信噪比的增加,IA-CS算法和BS-CS算法的DOA估计精度急剧增加,在信噪比门限以上其DOA估计性能明显优于其他算法。

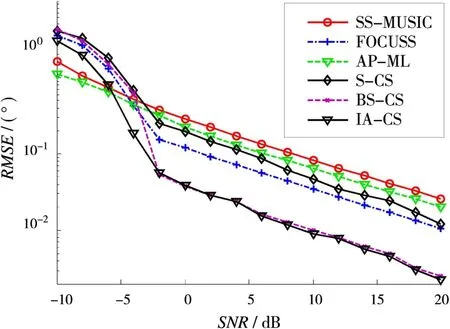
图2 仿真二信噪比变化时的性能曲线

仿真三:不同仰角对算法估计精度的影响

仿真条件:单个目标,目标高度为12 000 m,距离从50 km飞至650 km,信噪比为10 d B,快拍数为10。蒙特卡罗实验次数为100次。

图3给出几种算法进行100次独立实验的角度估计结果,其中实线为目标真实值。可以看出IA-CS算法和BS-CS算法性能优于其他两种传统DOA估计算法。

4 结束语

利用目标空域稀疏的特点,将压缩感知方法引入到DOA估计问题中,推导了协方差矩阵压缩感知、内插阵压缩感知和波束空间压缩感知DOA估计方法,将DOA估计问题视为1范数最优化问题,有效提高了算法的性能,并通过仿真和实测数据处理验证这几种方法的高分辨率和测角精度。计算机仿真结果表明,通过稀疏分析,为低信噪比和快拍数较少的环境下DOA估计提供了一种有效的解决方法。相比于应用最为广泛的子空间类算法,该算法在少量采样下更具有优势,类似子空间类算法,该算法随着采样点的增多可以提高估计效果,此外建立模型时并未要求信号源是相互独立的,因此对空域信号的相关性不敏感,可以直接用于相干信号的DOA估计,且具有更高的角度分辨率。

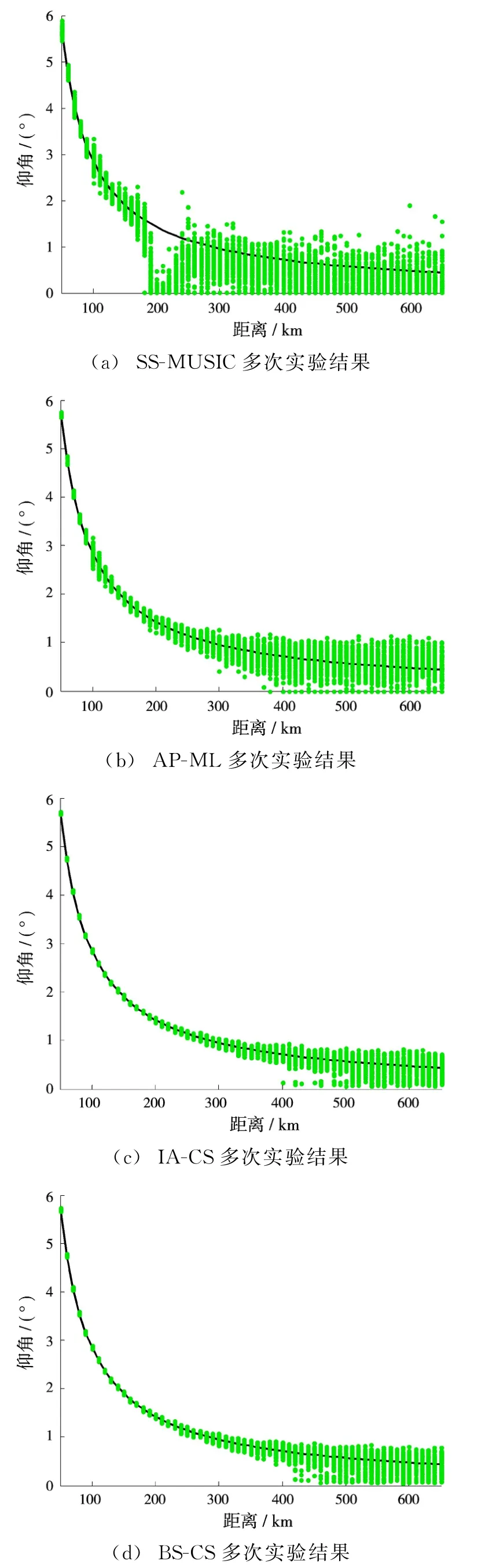
图3 几种算法多次实验结果

[1]CANDÈS E J.Compressive Sampling[C]∥International Congress of Mathematicians,Madrid,Spain:[s.n.],2006:1433-1452.

[2]焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1651-1662.

[3]王健,宗竹林.前视SAR压缩感知成像算法[J].雷达科学与技术,2012,10(1):27-31,36.

[4]MALIOUTOV D,CETIN M,WILLSKY A S.A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays[J].IEEE Trans on Signal Processing,2005,53(8):3010-3022.

[5]贺亚鹏,李洪涛,王克让,等.基于压缩感知的高分辨DOA估计[J].宇航学报,2011,32(6):1344-1349.

[6]CEVHER V,GURBUZ A C,MCCLELLAN J H,et al.Compressive Wireless Arrays for Bearing Estimation[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,Las Vegas,NV:IEEE,2008:2497-2500.

[7]WANG Y,LEUS G,PANDHARIPANDE A.Direction Estimation Using Compressive Sampling Array Processing[C]∥IEEE/SP 15th Workshop on Statistical Signal Processing,Cardiff:IEEE,2009:626-629.

[8]薛会祥,赵拥军.基于CS阵列的DOA估计[J].电子测量与仪器学报,2012,26(3):208-214.

[9]BILIK I.Spatial Compressive Sensing for Direction-of-Arrival Estimation of Multiple Sources Using Dynamic Sensor Arrays[J].IEEE Trans on Aerospace and Electronic Systems,2011,47(3):1754-1769.

[10]ZHU W,CHEN B X.Novel Methods of DOA Estimation Based on Compressed Sensing[J].Multidimensional Systems and Signal Processing,2015,26(1):113-123.

[11]NEEDELL D,VERSHYNIN R.Signal Recovery from Incomplete and Inaccurate Measurements via Regularized Orthogonal Matching Pursuit[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):310-316.

[12]薛会祥,赵拥军,郭磊.基于交替下降求解的稀疏信号重建算法[J].信息工程大学学报,2012,13(2):211-217.

[13]GILBERT A C,LI Y,PORAT E,et al.Approximate Sparse Recovery:Optimizing Time and Measurements[J].SIAM Journal on Computing,2012,41(2):436-453.

[14]ZHENG J,KAVEH M.Directions-of-Arrival Estimation Using a Sparse Spatial Spectrum Model with Uncertainty[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,Prague,Czech Republic:IEEE,2011:2848-2851.

[15]LI J.Improved Angular Resolution for Spatial Smoothing Techniques[J].IEEE Trans on Signal Processing,1992,40(12):3078-3081.

[16]ZHU W,CHEN B X.Altitude Measurement Based on Terrain Matching in VHF Array Radar[J].Circuits,Systems and Signal Processing,2013,32(2):647-662.

[17]GORODNITSKY I F,RAO B D.Sparse Signal Reconstruction from Limited Data Using FOCUSS:A Re-Weighted Minimum Norm Algorithm[J].IEEE Trans on Signal Processing,1997,45(3):600-616.