横向剪切干涉纯背景条纹模拟

代金梅，朱进容，2，姚育成，成纯富

（1湖北工业大学太阳能高效利用湖北省协同创新中心，湖北 武汉430068；2武汉理工大学材料科学与工程学院，湖北 武汉430070）

横向剪切干涉仪以平行平晶为分光元件，共光路的设计增强了干涉仪的抗震性，能够实时显示。由于其结构简单、对光学元件要求低，国内外学者采用这种干涉法对温度场、肥皂泡厚度、天然气管道泄漏等进行无损检测［1－4］。用 Zernike多项式表示光学系统像差，横向剪切干涉仪还能拟合出光学元件表面面形［5］。然而剪切条纹并不直接反映待测波面，即使在大剪切量的情况下，条纹退化为一组类似于全息干涉的条纹，仍包含背景条纹［6］。由此可见，纯背景条纹的研究将有助于分析光学系统定位误差，实现实验数据的快速处理。

本文根据横向剪切的成像理论，利用Matlab软件模拟横向剪切干涉纯背景条纹，分析离焦像差和附加相位差对条纹特征的影响。对比纯背景条纹的模拟和实验条纹，验证实际光学系统定位存在的误差，以指导光路的调试。

1 横向剪切干涉原理

平行光穿过二维轴对称测试段入射到平行平晶，经平行平晶前后两表面反射，在水平方向上错开一定的距离，相遇后形成剪切干涉条纹。若两波面在x方向错开距离（剪切量）S，则叠加后干涉波面的相位差

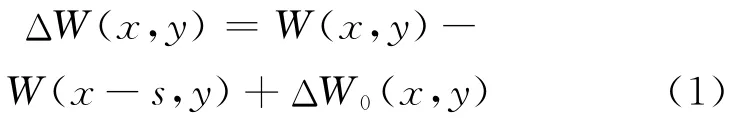
其中，W（x，y）和W（x－s，y）分别为平行平晶迎光面和背光面的待测波面，两者互为对偶相且信息等价；Δl为平行平晶引入的两剪切波面的几何光程差。

理论上，理想的横向剪切干涉纯背景（无待测场）条纹是一片均匀亮场。由于光学元件表面存在缺陷、平行平晶两表面不严格平行等，系统存在球差、像差等光学系统像差，实际观测到的纯背景干涉图将呈现弯曲互相的平行楔形条纹。根据光学系统的成像理论，初级像差（即三级像差）能很好地描述光学系统的像差。相应地，剪切前后的纯背景波面W0（x，y）、W0（x－s，y）以及干涉波面的相位差ΔW0（x，y）分别为:

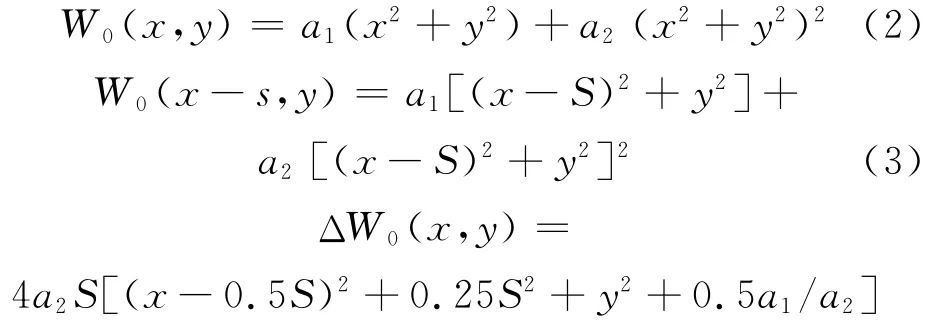
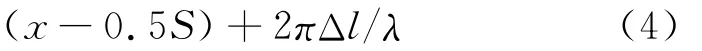
式中，a1、a2分别为近轴像点离焦像差和离轴像差。

作如下坐标变换

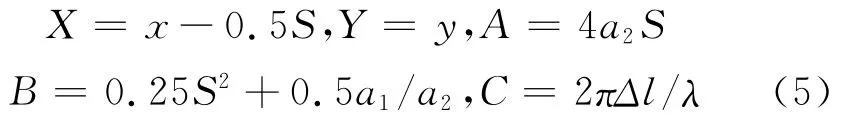
其中，C为附加相位差，与平行平晶的厚度和偏转角有关。整理式（4）得到

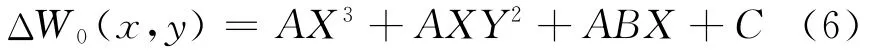
由上式可知，剪切干涉条纹相位分布是X的三次多项式、Y的二次多项式，故条纹在Y方向恒对称。从纯背景干涉图上提取3条水平线（即Y恒定）上的数据，三次多项式拟合后联立求解，可得到离焦a1、a2和C。

2 实验装置

横向剪切干涉仪的光路如图1所示。整个装置放置在精密光学减震平台之上。He-Ne激光器连续输出632.8nm的光波，采用可调衰减器调整光束强度以保护图像采集系统，90°反射后经小孔光阑滤掉杂散光。短焦距的半球透镜的扩束镜和长焦距的凸透镜构成扩束准直系统，将光束扩展为通光口径100mm的平行光束。平行平晶前后表面的两反射波面相遇形成的剪切干涉条纹经焦距200mm的凸透镜汇聚后由数码相机捕捉，最后存储于PC端。实验采用K9材质的平行平晶，折射率为1.51，直径100mm，厚度40mm。M1、M2、M3均为全反射镜面，用来改变光的传播方向和缩短光路。

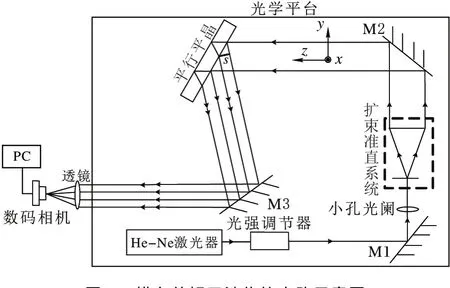
图1 横向剪切干涉仪的光路示意图

3 横向剪切干涉纯背景条纹的模拟结果

计算域半径50mm，纯背景条纹输出为灰度图，明暗条纹的灰度从256过渡到0，分辨率30pix/mm。K9材质高质量的双面平行平晶厚度40mm，折射率1.515。计算域外侧用黑色填充，条纹不可见一侧用灰色填充。

3.1 离焦像差a1的影响

平行平晶偏转角60°，计算出S＝24.2mm、C＝0.2πrad。调节扩束准直系统中半球透镜的位置可改变初级球差a1。若令球差a2＝－6.8×10－6π rad/mm4，离焦像差a1（－0.01～0.01πrad/mm2）对纯背景条纹的影响如图2所示。分析图可知，离焦像差a1对条纹形状影响很大。随着a1增大，条纹中心附近出现向外拓展的特殊椭圆轮廓，X方向的不对称性也越明显。当a1＝－0.01（a1＜0）时，条纹高度密集。当a1＝0时，椭圆轮廓较明显。当a1＝0.01时，条纹稀疏，对称中心两侧出现明暗相反的特殊椭圆轮廓；内部相位梯度无规则变化，外部等间距。

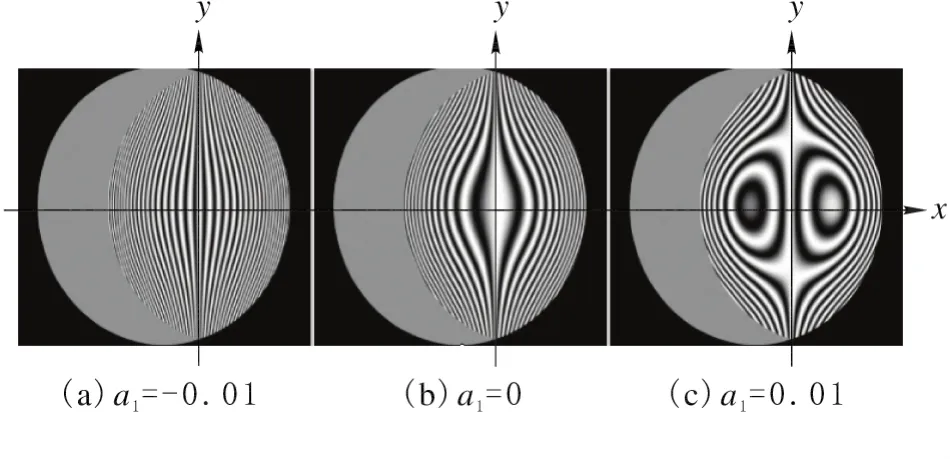
图2 离焦像差a1在－0.01～0.01内的纯背景模拟条纹

3.2 球差a2的影响

平行平晶偏转角设置60°，S和C的取值同上。令离焦像差a1＝0，讨论A＜0时球差a2对纯背景条纹的影响，模拟结果如图3所示。分析图可知，条纹分布在X方向仍明显不对称，对称中心两侧存在椭圆轮廓。球差a2对条纹的影响很大，从10－5πrad/mm4变为10－6πrad/mm4，仅降低一个数量级，条纹间距剧增。即a2太小，将没有足够的背景条纹作为参考；a2太大，条纹密集而难以分辨。因此，实验时需调试得到合适的a2值。

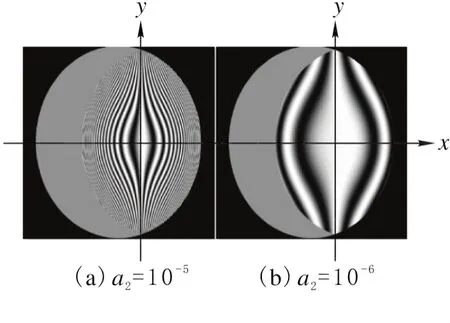
图3 不同数量级的球差b3的纯背景模拟条纹

3.3 附加相位差C的影响

由于光强表达式中的余弦函数以2π为周期，其他分布都可平移一个周期内的分布来得到。设定离焦像差a1＝2.9×10－2πrad/mm2，球差a2＝－6.8×10－6πrad/mm4，2π内C 对条纹分布特征的影响如图4所示。讨论如下:

1）C＝0πrad时，cos（ΔW0）＝cos（AX3＋AXY2＋ABX），条纹整体呈对称分布；

2）C＝0.5πrad时，cos（ΔW0）＝cos（AX3＋AXY2＋ABX＋0.5π）＝sin（AX3＋AXY2＋ABX），条纹分布将向右移动1/4周期，条纹在X方向正负半轴上明暗正好相反；

3）C＝πrad时，cos（ΔW0）＝cos（AX3＋AXY2＋ABX＋π）＝－cos（AX3＋AXY2＋ABX），条纹分布将向右移动1/2周期，对称性与1）相同，只是条纹明暗正好相反；

4）C＝1.5πrad时，cos（ΔW0）＝cos（AX3＋AXY2＋ABX＋1.5π）＝－sin（AX3＋AXY2＋ABX），条纹分布将向右移动2/3周期，对称性与2）相同，只是条纹明暗分布正好相反；

5）C＝2πrad时，cos（ΔW0）＝cos（AX3＋AXY2＋ABX＋2π）＝cos（AX3＋AXY2＋ABX），相位差分布将向右移动1个周期，条纹与1）完全相同。

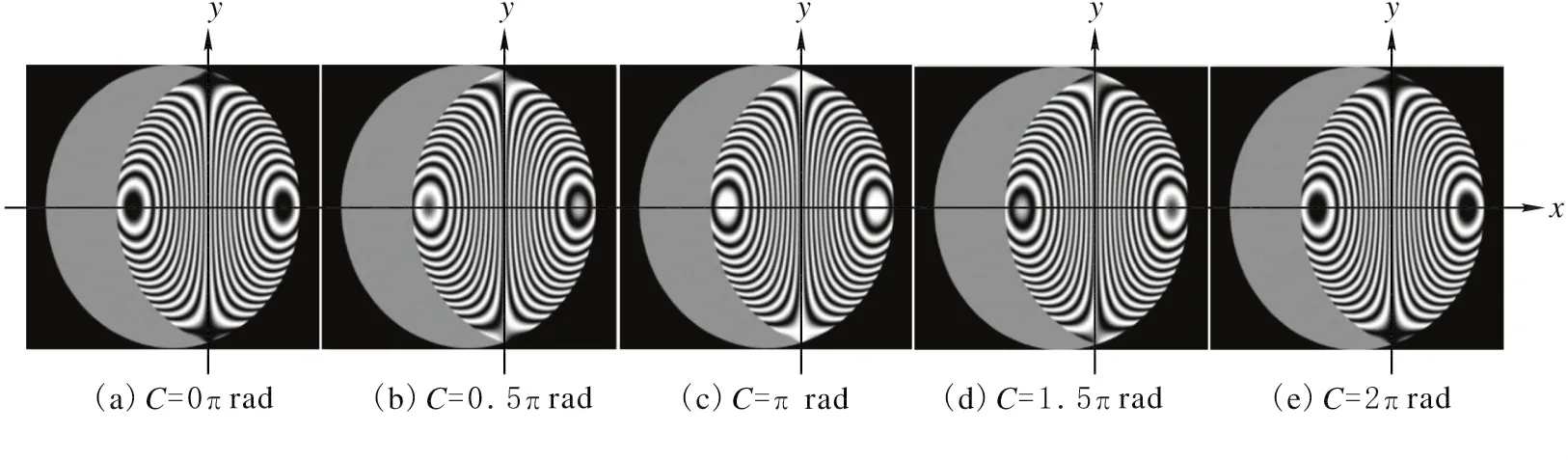
图4 C在0～2πrad周期内的纯背景模拟条纹

3.4 与实验结果对比

取纯背景干涉图上3条水平线上的数据，求解得到离焦a1＝2.88×10－2πrad/mm2、球差a2＝－6.81×10－6πrad/mm4、C＝0.16πrad。将这些系数带入到横向大剪切干涉成像的数学描述中，并赋予亮条纹He-Ne激光的颜色，纯背景干涉图的实验和模拟结果分别如图5所示。实验干涉只记录了部分视野范围内的干涉条纹，对应虚线宽内的模拟条纹。两者的条纹分布特征基本一致，在模拟结果的有效干涉区出现了2个并排椭圆轮廓。

图5 纯背景干涉图的实验和模拟结果

4 结论

1）纯背景条纹的相位分布规律性很强，竖直方向始终对称，水平方向的分布受附加相位差的影响，对称性呈周期性变化。

2）当扩束准直透镜组焦距失配时，平行光将明显汇聚或发散，像差较大使得条纹密集不易分辨。调试光路，可以获得适宜的像差系数，输出易于处理的纯背景条纹。

3）借助于Matlab软件纯背景模拟条纹与实验条纹基本一致。

［1］ Shakher C，Nirala A K.Measurement of temperature using speckle shearing interferometry［J］.Applied Optics，1994，33（11）:2 125-2 127.

［2］ Zhu Jinrong，Dai Jinmei，Cheng Xiaomin，et al.Temperature measurement of a horizontal cylinder in natural convection using lateral shearing interferometer with a large shear amount［J］，Optical Engineering，2015，54（03）:0 341 09-8-0 341 09-8.

［3］ Lv Wei，Zhou Huaichun，Lou Chun，et al.Spatial and temporal film thickness measurement of a soap bubble based on large lateral shearing displacement interferometry［J］.Applied optics，2012，51（36）:8 863-8 872.

［4］ 张学锋，高玉斌.新式横向剪切干涉系统对天然气管道泄漏野外监测的研究［J］.光谱学与光谱分析，2012，32（09）:2 587-2 590.

［5］ 彭爱华，叶红卫，李新阳.基于解耦差分泽尼克待定系数法的二维横向剪切波面重建算法［J］.光学学报，2011，31（08）:9-13.

［6］ 朱进容，张金业，陈义万.水平圆管表面自然对流换热的数值模拟［J］.湖北工业大学学报，2013，28（01）:1-3，21.