考虑应力水平的胶凝砂砾石坝安全分析
2015-01-16李秀琳吕小彬彭云枫
李秀琳,吕小彬,彭云枫
(1.中国水利水电科学研究院,北京,100038;2.流域水循环模拟与调控国家重点实验室,北京,100038;3.三峡大学水利与环境学院,湖北宜昌,443002)
0 引言
胶凝砂砾石坝是结合碾压混凝土坝和混凝土面板堆石坝优点而发展起来的一种新坝型,坝体断面一般设计为梯形。从结构稳定的角度看,采用对称梯形剖面的胶凝砂砾石坝是一种安全性较高的坝型[1]。
为研究分析胶凝砂砾石坝应力及安全特性,一些专家学者从不同角度做了计算分析。何蕴龙等[2]运用有限元法,以重力坝作为参照,计算分析了梯形胶凝砂砾石坝在各种荷载情况下的坝体应力和变形特点。计算结果反映出胶凝砂砾石坝在各种荷载工况下都有较好的工作性能,安全性较重力坝有很大提高。孙明权等[3-4]根据材料试验结果推出胶凝砂砾石材料的本构关系,并采用有限元非线性分析得出胶凝砂砾石坝的应力分布和应力水平分布规律合理。李永新等[5]提出了连续等效模型模拟层状胶凝砂砾石坝结构,应用强度储备系数法和APDL技术对静力状态下的胶凝砂砾石坝的应力稳定进行分析,认为胶凝砂砾石坝满足一定的应力稳定要求。熊堃等[6]运用不同的结构破坏分析方法对胶凝砂砾石坝进行计算分析,结果表明胶凝砂砾石坝坝趾、坝基面部位较为薄弱,易发生破坏。
文献[6]的计算成果表明胶凝砂砾石坝整体安全性较高,结构破坏主要发生在小部分区域。为进一步分析胶凝砂砾石坝的安全性,采用有限元法对等高程的胶凝砂砾石坝和重力坝进行计算,分析两种坝型在空库、上游1/3坝高和满库水位下的应力分布情况,采用应力水平、点安全系数法分析两种坝型的抗剪、抗滑稳定情况。基于计算分析评价胶凝砂砾石坝的安全特性,分析结果可为胶凝砂砾石坝的工程应用提供借鉴。
1 理论基础及计算方法
1.1 应力水平
应力水平是实际主应力差和破坏时主应力差的比值,反映了实际剪应力与材料抗剪强度的比值关系,即材料强度的发挥程度。应力水平的表达式为[4]:

式中:σ1-σ3为单元的偏应力;(σ1-σ3)f为材料的峰值强度。
基于孙明权教授胶凝砂砾石材料大三轴试验结果,对其试验数据进行回归分析,得出不同胶凝含量的胶凝砂砾石材料(σ1-σ3)/pa-(σ3pa)曲线[7],如图1所示。围压与强度关系可以用指数函数表述,压缩状态下胶凝砂砾石破坏强度与围压满足关系式[7]:

式中:a、b为材料的试验参数,可由试验得出;pa为标准大气压力。
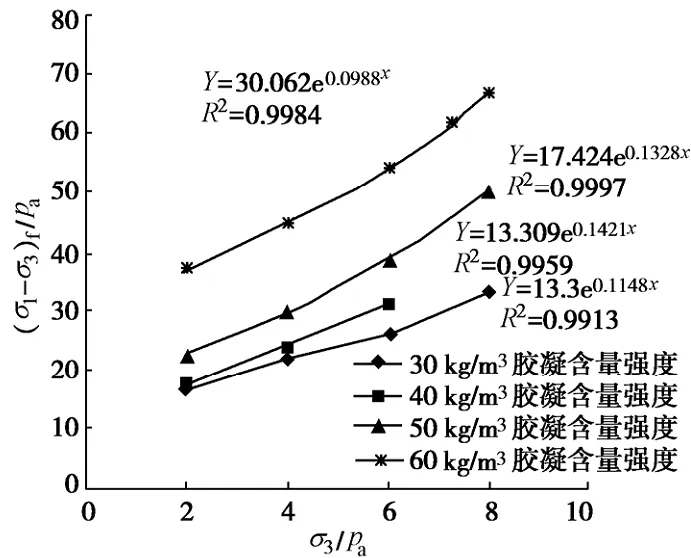
图1 (σ1-σ3)/pa- σ3/pa曲线Fig.1 Curve of(σ1-σ3)/pavs.σ3/pa
故胶凝砂砾石材料应力水平可表示为:

通过对比强度试验和抗折强度试验,胶凝砂砾石的抗拉强度比接近1∶8,因此在考虑胶凝砂砾石材料拉伸状态下的弹性模量时将抗拉强度取强度的1/8[7]。故拉伸状态下,胶凝砂砾石材料的应力水平表达式为:

对于混凝土材料,峰值强度可表示为[8]:

式中:fc为混凝土材料单轴抗压强度;kc为强度系数。故混凝土材料应力水平表达式为:

1.2 点抗滑稳定安全系数
对于建基面上的某点,基于摩尔-库伦准则,其点安全系数可以定义为:

式中:摩擦系数f=tanφ,φ、c分别为材料的摩擦角和凝聚力;σn、τn分别为截面上的正应力和切应力。
式(7)表示截面在正应力水平下的极限切应力强度与该截面切应力的比值。由式(7)可以看出,一个应力点对应的每一个截面都有一个安全系数,其中点安全系数最小的截面为最危险截面。在实际应用中对式(7)求极值,找出最小安全系数及其所对应的最危险截面[9]。通过计算推导得出建基面上一点的最小安全系数为:
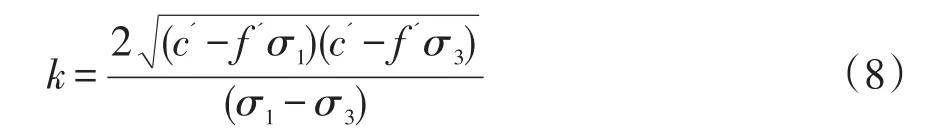
式中:σ1和σ3分别为最大和最小主应力;c'、f'分别为建基面凝聚力与摩擦系数。其与最小点安全系数对应的最危险截面方向角α(最危险截面法线方向与最大主应力的夹角)满足条件:

2 有限元模型
某胶凝砂砾石坝坝高100 m,上、下游坡的坡比都为1∶0.7,溢洪道放置在坝身,上游面布置钢筋混凝土面板防渗,上游护面的下部安装了多孔排水管直至排水廊道,并连接至导流隧洞。坝体不设纵缝,横缝间距为30 m。设计一等高程重力坝与该坝进行对比分析。
坝体承受自重、静水压力和扬压力,为研究胶凝砂砾石坝在不同水位条件下的应力变化情况,设计空库(工况一)、1/3坝高水位(工况二)和满库(工况三)三种工况进行计算,下游均为无水。其中假定扬压力在防渗帷幕处折减为水头的1/2,在排水孔处折减为水头的1/4,扬压力在坝底线性分布,坝基两侧采用法向约束,基底采用铰约束。计算时采用参数如表1所示。
计算区域为坝基范围向上、下游方向和坝基深度方向各延伸2倍坝高。网格划分采用四节点单元,胶凝砂砾石坝共5 100个节点,4 280个单元;重力坝共4 134个节点,3 720个单元。胶凝砂砾石坝和重力坝网格划分如图2所示。

表1 计算参数Table 1 Calculation parameters

图2 有限元计算网格划分Fig.2 Finite element mesh
3 应力及应力水平计算分析
3.1 应力计算分析
计算时胶凝砂砾石材料屈服条件为摩尔-库伦破坏准则,坝基与重力坝坝体材料采用理想弹塑性本构模型。应力计算结果压应力为负、拉应力为正。胶凝砂砾石坝和重力坝最大主应力和最小主应力最值情况如表2所示,满库时主应力分布情况如图3、图4所示。
由表2及图3、图4可以得出,重力坝应力分布随水位增加变化较大,空库时最大压应力位于坝踵区,满库时,最大压应力位于下游坝趾区;满库时上游坝踵区出现较大拉应力。随着水位升高,由于水压力和扬压力的增大使重力坝最小主应力最值减小。
空库和1/3库水位时胶凝砂砾石坝没有出现拉应力,全断面受压;满库时会在坝踵处出现应力集中,但仅有一个节点出现拉应力,且远小于胶凝砂砾石材料90 d龄期抗拉强度0.86 MPa。从最小主应力看,胶凝砂砾石坝的应力较低,100 m高的胶凝砂砾石坝满库坝趾处最大压应力为2.399 MPa。坝体大部分区域压应力不超过1.50 MPa,只有满库时坝踵处会有小范围应力集中,坝体无拉应力出现。同等高度的土耳其奥尤克坝在施工时分别对坝踵和坝趾采用高强度的胶凝砂砾石材料和混凝土进行了加固[8]。
满库时重力坝需要4.262 MPa抗压强度,胶凝砂砾石坝需要2.399 MPa抗压强度抵抗压应力,所需抗压强度大约为重力坝的56%;重力坝坝踵区产生的拉应力为0.958 MPa,而胶凝砂砾石坝拉应力为0.188 MPa。由于坝体需有足够的拉应力抵抗,混凝土拉应力一般为压应力的10%,故重力坝为获得0.958 MPa拉应力,其抗压强度为9.58 MPa,胶凝砂砾石坝的压应力需要1.88 MPa,即满库工况下胶凝砂砾石坝的强度要求仅仅是重力坝的19.6%。
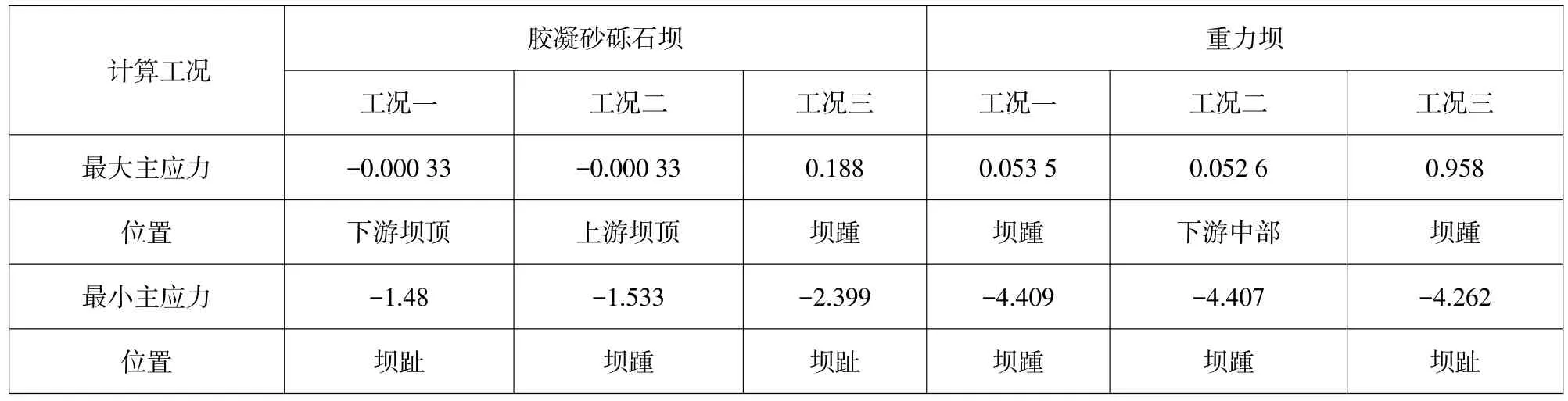
表2 坝体主应力最值表(单位:MPa)Table 2 The extremums of maximum and minimum principal stress of dams
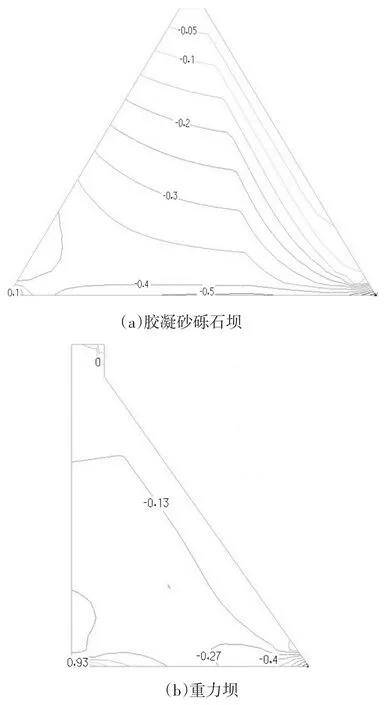
图3 满库工况下最大应力分布图(单位:MPa)Fig.3 Distribution of maximum principal stress under the condi⁃tion of full pool

图4 满库工况下最小应力分布图(单位:MPa)Fig.4 Distribution of minimum principal stress under the condi⁃tion of full pool
此外,胶凝砂砾石坝的剪应力很小,且分布均匀,重力坝的剪应力较大。重力坝为了抵抗剪应力,筑坝时需要将基岩与坝体整体化,胶凝砂砾石坝不需要整体化。
综合比较最大主应力、最小主应力和剪应力数值及分布情况可以得出:同等高程的胶凝砂砾石坝比重力坝整体应力水平低,应力分布合理。
3.2 应力水平计算分析
胶凝砂砾石筑坝材料体积质量为100kg/m3,对于式(3)、式(4)中参数,取a=40.186,b=0.024 7。pa取101.325 kPa,e近似取2.718 28。应力水平可以反映材料剪切强度的发挥程度,若s>1,说明单元已经发生剪切破坏。坝体应力水平最大值及其位置如表3所示。
从表3可以得出,不同工况时胶凝砂砾石坝的应力水平最大值均出现在坝趾处,重力坝出现在坝踵或坝趾处。两种坝的应力水平最大值与剪应力最大值基本处于同一区域。三种工况下,两种坝型应力水平均小于1,说明坝体不会产生剪切破坏,但重力坝应力水平最大值整体较高。胶凝砂砾石坝应力水平最大值随上游水位升高而逐渐增大,而重力坝应力水平随上游水位升高逐渐减小。满库工况下应力水平分布如图5所示。

表3 应力水平最大值分布表Table 3 Distribution of maximum stress level

图5 满库工况下应力水平分布图Fig.5 Distribution of maximum stress level under the condition of full pool
由图5可以得出,胶凝砂砾石坝的应力水平分布均匀,整体变化趋势较缓,筑坝材料的强度可以得到充分发挥,应力水平值随坝高增大而减小,未出现应力水平集中。重力坝应力水平由上游区向下游变化较大,会产生突变,在坝趾区域出现应力集中情况,满库时胶凝砂砾石坝最大值相对较大。
应力水平分析结果表明,不同水荷载作用下胶凝砂砾石坝虽未发生剪断破坏,但在坝趾区域应力水平均为最高,说明该区域安全性相对较低,需引起重视并在设计时注意加固。
4 抗滑稳定分析
胶凝砂砾石坝相较于重力坝坝体断面较大,容重与混凝土接近,并且其上游倾斜可利用水重,有利于保持坝体稳定。采用刚体极限平衡原理计算坝体的整体抗滑稳定系数没有考虑滑动面上的实际应力分布,也未考虑滑动面上部与下部结构相对变形对抗滑稳定的影响。而结构计算与试验均表明:应力分布在滑动面上是不均匀的,滑动面上各点的抗剪强度和抗剪安全系数也不一样,因此应根据各点的受力状态,计算各点的点安全系数[10]。通过坝体受力分析可知,胶凝砂砾石坝体应力水平较低,且分布均匀,但是在坝踵和坝趾处会存在应力集中情况,因此通过点抗滑安全系数来判别坝基面的抗滑稳定更加科学合理。对式(8)中参数,坝基面凝聚力与摩擦系数c'、f'分别取0.5 MPa和0.5,两种坝体在坝基面点最小抗滑稳定系数如图6所示。
由图6可以发现,对于重力坝,在空库和1/3库水位工况时,点最小抗滑稳定安全系数均大于1,从坝踵开始逐渐增大,在距坝趾7 m时下降;满库时从距坝踵18 m时开始减小,且满库时最小安全系数远小于1,因此会发生滑动破坏。对于胶凝砂砾石坝,坝基面点最小抗滑安全系数均大于1,最小值为1.27,出现在满库时下游坝趾处,整体变化较为平缓;离开坝踵后,点最小抗滑稳定安全系数会有一定升高;由于坝趾区剪应力较大,坝踵区压应力较小,故在这两个区域附近,点安全抗滑稳定系数较小,可进行地基处理,以提高层面抗滑稳定性能,在坝踵区提高层面凝聚力较有效,而在坝趾区提高摩擦系数更为有效。
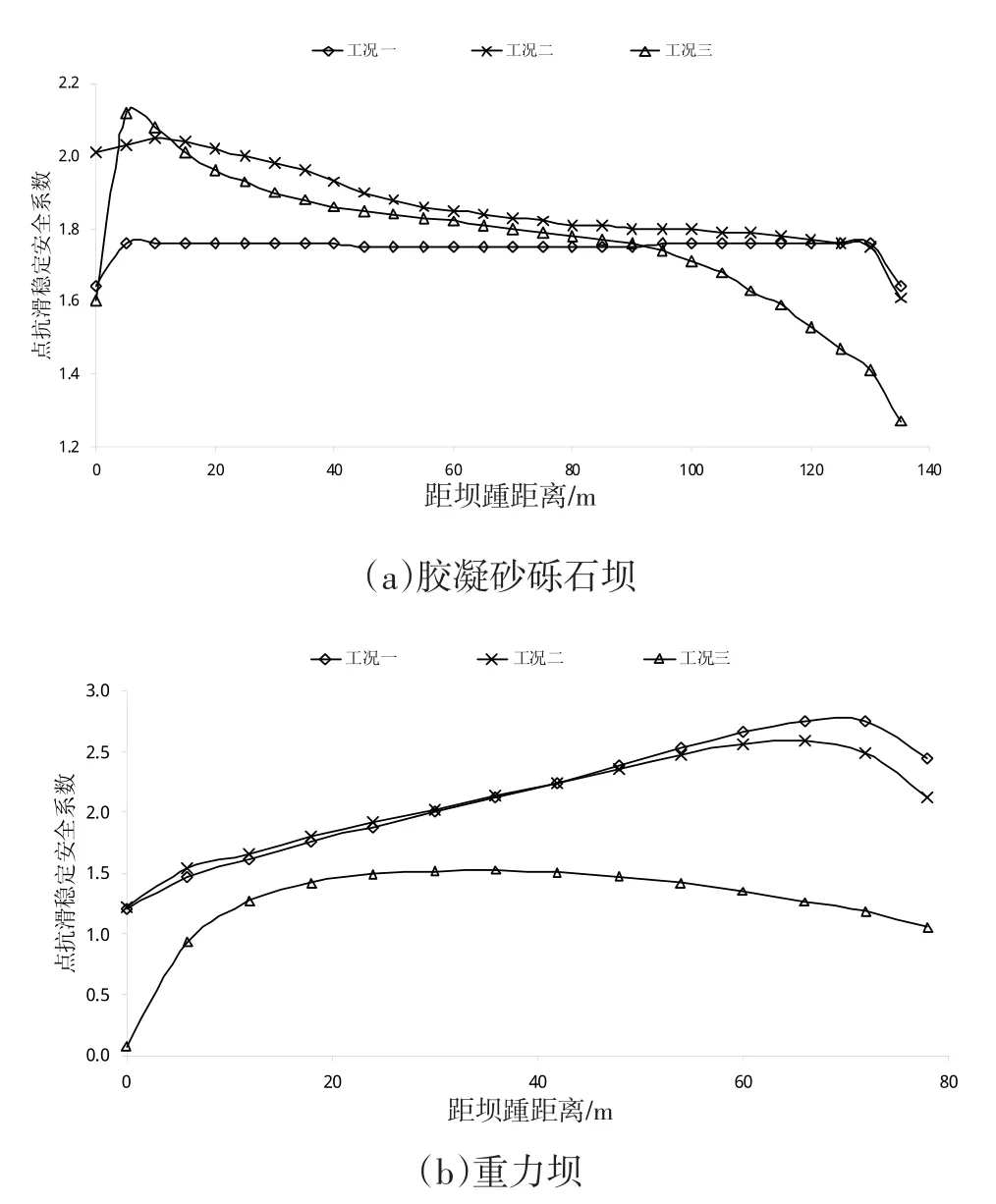
图6 建基面最小点抗滑稳定安全系数Fig.6 The minimum point anti-slide safety factor of base sur⁃face
抗滑稳定分析表明,在不同水荷载作用下胶凝砂砾石坝均能保持稳定,在满库工况下,相较于等高程重力坝安全性更高。
5 结语
通过对比分析不同工况下胶凝砂砾石坝和重力坝应力、应力水平及抗滑稳定计算结果,可以得到以下结论:
(1)同等高程的胶凝砂砾石坝比重力坝整体应力水平低,应力分布合理。胶凝砂砾石坝应力水平随坝高增大而减小,未出现应力水平集中,重力坝应力水平由上游区向下游逐渐增大,在坝趾区域出现应力集中情况。
(2)重力坝在空库和1/3库水位工况时,点最小抗滑稳定安全系数均大于1,满库时最小安全系数远小于1,建基面会发生滑动破坏。胶凝砂砾石坝最小抗滑安全系数均大于1,整体变化较为平缓。由于坝趾区剪应力较大,坝踵区压应力较小,在这两个区域附近,点安全抗滑稳定系数较小。
未考虑胶凝砂砾石材料的非线性特征,实际情况中胶凝砂砾石材料应力应变关系具有明显的弹塑性性质和应变软化等特性,有待深入研究。
[1]彭云枫,何蕴龙,熊堃.Hardfill坝结构安全性分析[J].中国水利,2007(21):55-57.
[2]何蕴龙,彭云枫,熊堃.Hardfill坝结构特性分析[J].水力发电学报,2008,27(6):68-72.
[3]孙明权,杨世锋,张镜剑.超贫胶结材料本构模型[J].水利水电科技进展,2007(6):35-37.
[4]孙明权,彭成山,陈建华,等.超贫胶结材料坝非线性分析[J].水利水电科技进展,2007(8):42-45.
[5]李永新,何蕴龙,乐治济.胶结砂砾石坝应力与稳定有限元分析[J].中国农村水利水电,2005(7):35-38.
[6]熊堃,何蕴龙,曹学兴.基于不同结构破坏分析方法的Hardfill坝破坏模式研究[J].水力发电,2012,38(8):36-39,43.
[7]蔡新,武颖利,李洪煊,等.胶凝堆石料本构特性研究[J].岩土工程学报,2010,32(9):1340-1344.
[8]刘俊林,何蕴龙,熊垄,等.Hardfill材料非线性弹性本构模型研究[J].水利学报,2013,44(4):451-461.
[9]樊赟赟,王思敬,王恩志,等.岩土材料剪切破坏点安全系数的研究[J].岩土力学(增刊),2009,30(2):200-203.
[10]杨会臣.胶凝砂砾石坝结构设计研究与工程应用[D].北京:中国水利水电科学研究院,2013.
