深覆盖层上某心墙坝渗流场与应力场耦合分析

吕高峰，张奕泽

（1.国家能源局大坝安全监察中心，浙江杭州，310014；2.中国电建集团华东勘测设计研究院有限公司，浙江杭州，310014）

0 前言

深厚覆盖层主要指堆积在河流河谷当中的第四纪松散沉积物，由漂石、卵砾石、块碎石及中粗、中细砂等组成。深厚覆盖层具有分布规律差、级配变化大、结构特别松散、渗透性强、岩性不均匀等特点。覆盖层成因的不同导致其物质成份差异较大，进而物理力学特性差异很大，使水电工程建设经常遇到地基承载力不够、不均匀变形大、渗透性大且渗流不够稳定等问题。在深厚覆盖层上建坝，覆盖层的性质对工程的安全有很大影响，覆盖层中的渗流特性和物理力学特性在建坝过程和运行过程中都会发生变化，渗流场和应力场相互影响，因此，在对建在深厚覆盖层上的工程进行计算分析时有必要考虑渗流场与应力场的耦合作用。

1 工程概况

某水电站大坝为砾石土直心墙堆石坝，坝顶高程856.00 m，最大坝高186 m，坝顶宽14 m。坝址河谷狭窄，谷坡陡峻，两岸山体拔河400～500 m，谷坡一般35°～50°，坝基为70余m深的深厚覆盖层。采用两道厚度为1.2 m的混凝土垂直防渗墙，上游墙为插入式，下游墙为廊道式，下游墙位于坝轴线，两墙中心线相距14 m，防渗墙最大深度约70 m。上游坝坡1∶2和1∶2.25，下游坝坡1∶2，坝体底宽约800 m，坝顶长573 m，围堰与坝体结合，坝体填筑总量约2 355万m3。坝体断面主要分为四个区:砾石土心墙、反滤层、过渡层和堆石区。坝体典型断面见图1。

2 渗流场与应力场耦合数学模型

根据孔隙水与固体颗粒的质量守恒原理建立连续性方程，结合固体颗粒的平衡微分方程和流体中的达西定律得出基本微分方程，其中土骨架采用非线性邓肯模型。

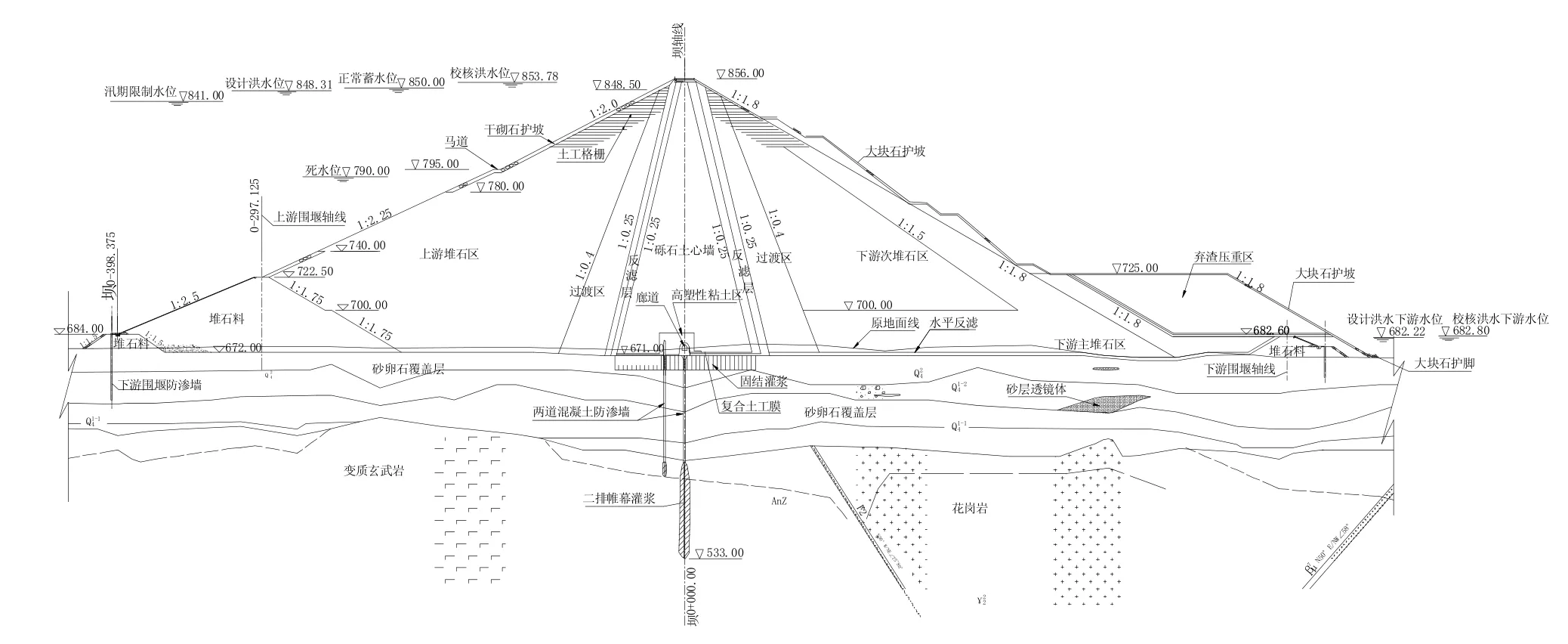
图1 坝体典型断面图Fig.1 Typical section of the dam

在土体中取一微小的单元体，并且z坐标以竖直向上为正，应力以压为正，将土骨架本构方程、几何方程代入平衡方程，采用有效应力原理，可得三维比奥固结微分表达式：

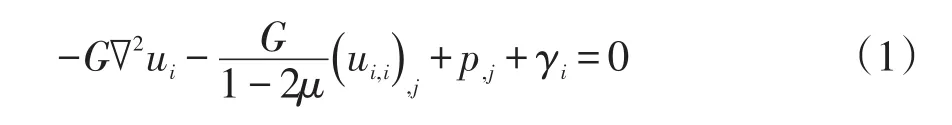
式中：G是剪切模量；μ是泊松比；ui是位移张量；γi是体积力张量；p是孔隙压力。

结合达西定律和渗流连续性，可得有限元控制方程：

式中：[ks]是单元劲度矩阵；[kc]是单元耦合矩阵；[kh]是单元渗流矩阵；Δδe是单元节点位移增量；ΔHe是单元节点水头增量；ΔRe是单元等效节点荷载；ΔQe是单元等效节点流量；θ是加权因子；t是时间。式中包含了3个位移未知量和1个水头未知量。利用边界条件和初始条件就可以求出这些未知量。

由于多孔介质的渗透系数与其孔隙率的分布情况密切相关，土体孔隙率、孔隙比的变化必然引起渗透系数的改变，其渗透场也因此而改变。大量试验表明，土体的初始渗透系数k'与渗透系数k之间可以用孔隙率n或孔隙比e的函数来表示：

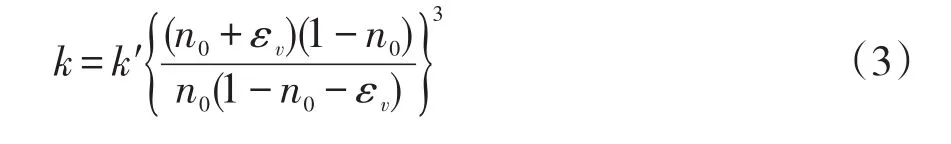
式中：εv是土体的体积应变。

3 有限元模型、参数与模拟方式

3.1 计算网格

建模选取河谷中间覆盖层最深处的典型断面，网格区域包括坝轴线以上520 m到坝轴线往下580 m，在高程方向，网格从坝顶高程856 m到基岩高程550 m，包含所有覆盖层和部分基岩。有限元网格见图2。

图2 有限元网格Fig.2 The finite element mesh

3.2 计算参数

计算中覆盖层、坝体主堆石、次堆石、过渡层、反滤层、混凝土和山体均采用邓肯-张E-B模型，心墙和高塑性粘土采用邓肯-张E-V模型，具体参数见表1和表2。

表1 坝体及覆盖层材料的E-B模型参数Table 1 Parameters of dam and overburden material in E-B model

表2 心墙和高塑性土的E-V模型参数Table 2 Parameters of core wall and high-plastic soil in E-V model

3.3 初始应力的模拟

3.3.1 覆盖层初始应力

因覆盖层是经过多年沉积而成，覆盖层呈超固结状态。计算中，可以将覆盖层简化作为坝体进行填筑。将填筑结束后计算所得应力作为基岩和覆盖层的初始应力。这样计算在一定程度上能够反映覆盖层的初始应力。

3.3.2 坝体单元初始应力

对于坝体单元，将每一级坝体填筑完成时的自重应力作为该级坝体填筑的初始应力。

4 计算结果分析

4.1 变形

图3是典型断面竣工期与蓄水期顺河向位移等值线图。由图可知：坝体填筑结束后，坝体顺河向位移整体呈对称分布，因上游主堆石区材料优于下游次堆石区，心墙上游坝体往上游的顺河向位移为9 cm，小于心墙下游坝体往下游的顺河向位移（12 cm）。蓄水后，坝体整体受到朝向下游的顺河向推力，坝体整体往下游变形，但心墙上游坝体变形较小，下游坝体变形较大，而心墙上游坝体的上部位移较大，下部较小，心墙上游坝体指向上游的顺河向位移最大为7 cm，较竣工期减小2 cm，心墙下游坝体的上部位移增大较大，下部位移增大较小，指向下游的顺河向位移最大为21 cm，较竣工期增大9 cm。

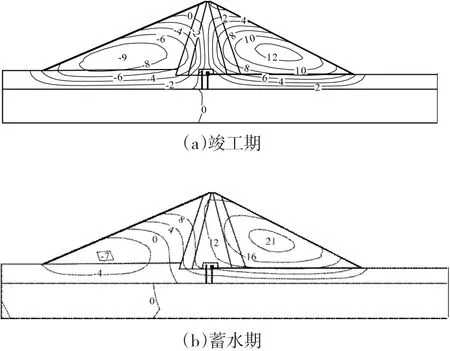
图3 坝体典型断面顺河向位移（单位：cm）Fig.3 Displacement along the river of typical section

图4是典型断面竣工期与蓄水期竖向位移等值线图。由图可知：坝体竣工后，坝体最大沉降为180 cm，发生在坝体中间1/2高程处。水库蓄水，上游侧坝体受到竖直向下的压力，使坝体竖向的总应力增大，同时蓄水也使坝体内孔隙水压力增大，从而减小有效应力引起坝体的回弹。经两者的综合作用，蓄水后坝体最大沉降为186 cm，较竣工期增大6 cm，位置依旧在坝体中间1/2高程处，但有略微往上游方向移动。

图4 坝体典型断面竖向位移（单位：cm）Fig.4 Vertical displacement of typical section

图5是蓄水后坝体典型断面特征点A（心墙中部典型节点，见图2）竖向位移变化曲线。由图可知：坝体蓄水初期，特征点A沉降速度较快，后期沉降速率逐步减小，约190 d后，沉降趋于稳定。

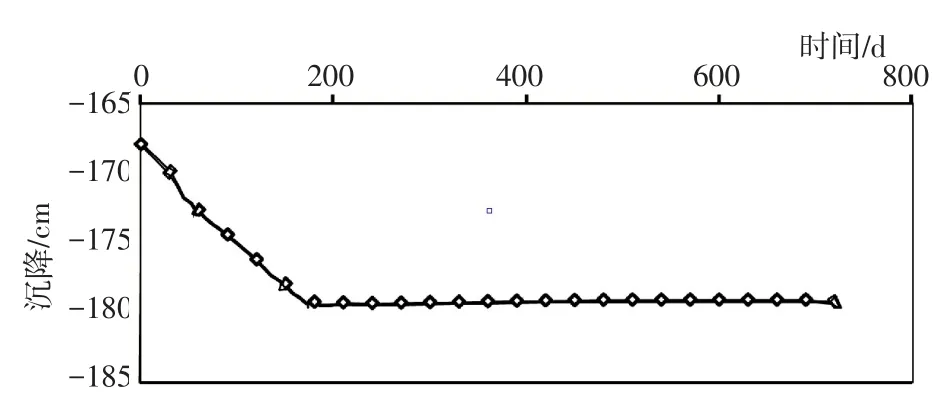
图5 蓄水后坝体典型断面特征点A竖向位移变化曲线Fig.5 Variation of vertical displacement of characteristic point(A)after impoundment

4.2 应力

图6是蓄水期典型断面大主应力和小主应力等值线图。由图可知：大主应力主要受上部荷载影响，在高程方向，由上往下逐步增大，基岩底部大主应力最大。心墙大主应力略小于坝体，具有一定的拱效应现象。坝体和表层覆盖层内小主应力在高程方向呈现上小下大的规律，在基岩内，小主应力很小。

4.3 水头与浸润线

图7是蓄水期30 d浸润线和水头等势线分布图。由图可知：水头主要在心墙和防渗墙处折减，等势线在心墙内较均匀分布，在心墙下游浸润线基本接近水平直线。

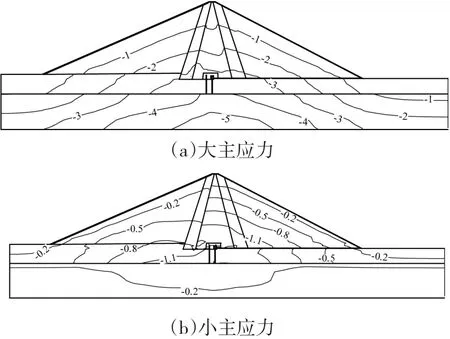
图6 蓄水期坝体典型断面应力（单位：MPa）Fig.6 Stress of typical section in impoundment period(MPa)

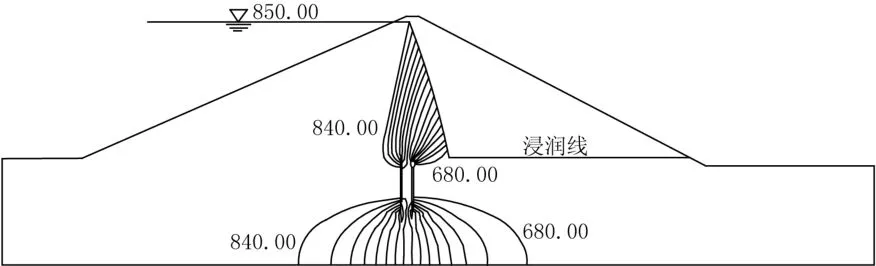
图7 蓄水30 d浸润线与水头等势线分布图（单位：m）Fig.7 Distribution of saturation line and equipotential line of wa⁃ter head in 30 days after impoundment

考虑耦合后蓄水60 d、90 d和120 d及不考虑耦合的水头等势线整体上与蓄水30 d的水头等势线没有明显区别。但在变形较大的部位水头等势线有微小的区别。以覆盖层为例，图8和图9分别是防渗墙上游和下游覆盖层内考虑耦合不同时期与不考虑耦合水头分布图，由图可知：

（1）考虑耦合蓄水30 d、60 d、90 d和120 d的水头分布曲线基本接近重合，即在考虑耦合情况下，蓄水时间的变化对水头等势线的影响极小。

（2）考虑耦合与不考虑耦合在覆盖层内的水头等势线有较小的区别，远离坝轴线的部位不考虑耦合与考虑耦合的水头分布基本重合，越靠近坝轴线差距越大。呈现上述规律主要是因为考虑耦合后，覆盖层因坝体填筑而产生沉降变形，导致覆盖层的孔隙率减小，渗透系数减小。远离坝轴线的覆盖层受坝体填筑影响产生的变形小，所以考虑耦合与不考虑耦合的水头差别小；靠近坝轴线的覆盖层受坝体填筑影响产生的变形大，所以考虑耦合与不考虑耦合的水头差别大。

（3）在坝轴线上游相同坝轴距上，考虑耦合后的水头值小于不考虑耦合的水头值；在坝轴线下游相同坝轴距上，考虑耦合后的水头值大于不考虑耦合的水头值。考虑耦合后，覆盖层渗透系数有一定的降低，在覆盖层内的水头折减值较不考虑耦合的水头折减值增大，所以考虑耦合后上游侧覆盖层内的水头较不考虑耦合的小，而下游呈现相反的规律。

图8 防渗墙上游覆盖层内考虑耦合不同时期与不考虑耦合水头分布图Fig.8 Distribution of water head of overburden located up⁃stream of cutoff wall under each condition

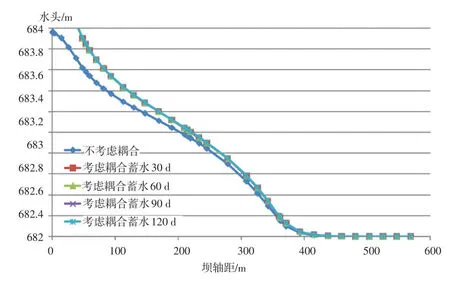
图9 防渗墙下游覆盖层内考虑耦合不同时期与不考虑耦合水头分布图Fig.9 Distribution of water head of overburden located down⁃stream of cutoff wall under each condition

4.4 孔隙率与渗透系数

图10是蓄水期覆盖层孔隙率与渗透系数沿顺河向分布图。由图可知：经过坝体填筑和蓄水，覆盖层受上覆荷载而压缩变形，覆盖层的孔隙率减小。顺河向X为0处受覆盖层内两道防渗墙的顶托作用，其变形较小，孔隙率变化不大。远离坝体的覆盖层内孔隙率变化较小，变形较大的覆盖层孔隙率变化较大。随着蓄水时间的延长，覆盖层变形逐步增大，其孔隙率逐步减小。覆盖层渗透系数的变化规律与孔隙率的变化规律一致。

图10 蓄水期覆盖层孔隙率与渗透系数沿顺河向分布图Fig.10 Distribution of porosity and osmotic coefficient along the river in overburden during impoundment period

5 结语

以某覆盖层上的心墙坝为例，运用渗流场与应力场耦合理论计算其应力变形，并分析蓄水后覆盖层的渗透系数和孔隙率的变化规律，得出了以下几点结论：

（1）在竣工期，坝体顺河向位移和沉降位移整体呈现上下游对称分布。蓄水后，心墙上游侧的顺河向位移增大值明显小于心墙下游侧坝体的顺河向位移增大值，但心墙上游侧上部顺河向位移增大较大，沉降位移较竣工期有较小增大，且沉降位移最大值部位有微小向上游方向移动。

（2）大主应力主要受上部荷载影响，心墙大主应力略小于坝体，具有一定的拱效应现象。

（3）坝体蓄水初期，坝体变形速率较大，后期沉降速率逐步减小，并逐步趋于稳定。

（4）在考虑耦合情况下，蓄水时间的变化对水头等势线的影响极小。考虑耦合与不考虑耦合在覆盖层内的水头等势线有较小的区别，远离坝轴线的部位不考虑耦合与考虑耦合的水头分布基本重合，越靠近坝轴线差距越大。在坝轴线上游相同坝轴距上，考虑耦合后的水头值小于不考虑耦合的水头值；在坝轴线下游相同坝轴距上，考虑耦合后的水头值大于不考虑耦合的水头值。

（5）覆盖层的孔隙率与渗透系数受覆盖层变形影响较大，变形较大的覆盖层孔隙率与渗透系数变化较大。覆盖层变形随着蓄水时间逐步增大，其孔隙率与渗透系数随着蓄水时间逐步减小，但速率都逐步减小。防渗墙因刚度较大，具有顶托作用，其变形较小，其附近覆盖层孔隙率与渗透系数变化不大。

[1]殷宗泽.土工原理[M].北京：中国水利水电出版社，2007.

[2]刘斯宏,王柳江.深厚覆盖层上心墙堆石坝防渗墙应力变形特性及其影响因素分析[C].土石坝技术2009论文集.北京：中国电力出版社,2009：217-226.

[3]平扬,白世伟,徐燕萍.深基坑工程渗流-应力耦合分析数值模拟研究[J].岩土力学，2001，22(1)：37-41.

[4]邹玉华,陈群,谷宏海.心墙堆石坝应力状态对渗流场影响的有限元分析[J].岩土力学，2011，32(7):2177-2183.

[5]顾唯星.深厚覆盖层心墙堆石坝应力场与渗流场耦合计算分析[D].南京：河海大学，2011.

[6]杨荣.瀑布沟高土石坝三维非线性分析[J].应用基础与工程科学学报，1995，(3):261-267.

[7]李勇泉.渗流场与应力场的耦合分析及其工程应用[D].武汉：武汉大学，2010.

[8]罗晓辉.深基坑开挖渗流与应力耦合分析[J].工程勘察,1996,(6):37-41.

[9]王晓鸿，仵彦卿.渗流场-应力场耦合分析[J].勘查科学技术,1998,(4):3-6.

[10]柴军瑞,仵彦卿.均质土坝渗流场与应力场耦合分析的数学模型[J].陕西水力发电，1997,13(3):4-7.

[11]陈晓平,茜平一,梁志松.非均质土坝稳定性的渗流场和应力场耦合分析[J].岩土力学,2004,25(6):860-864.

[12]陈益峰,胡冉,周嵩.高堆石坝水力耦合模型及工程应用[J].岩土工程学报，2011,33(9):1340-1347.

[13]吕高峰,王柳江,严俊.流固耦合对深厚覆盖层内防渗墙应力变形的影响[J].水力发电,2012,38(12)：22-24,30.

[14]刘斯宏,吕高峰.考虑流变效应的响水涧抽水蓄能电站上水库主坝长期变形预测[C].土石坝技术2011论文集.北京：中国电力出版社,2011:450-458.

[15]吕高峰,朱锦杰.覆盖层开挖深度对闸底板沉降的影响分析[J].大坝与安全.2014,(1):37-40.