应用三维多重网格法的极限平衡法分析锦屏一级拱坝右岸坝坡稳定性
2015-01-16陈平龙王文芬
陈 晨,陈平龙,王文芬
(1.江苏建筑职业技术学院,江苏徐州,221116;2.河海大学水利水电学院,江苏南京,210098;3.江苏省徐州市水利局,江苏徐州,221000)
0 前言
混凝土高拱坝的迅速发展使其成为大型水电站枢纽布置的主要坝型之一。相对于其他坝型而言,拱坝对地形地质条件的要求较高。拱坝主要依靠两岸坝肩岩体来维持自身的稳定,因此控制坝肩变形并保持稳定成为拱坝设计中一项重要的任务。目前坝肩稳定分析主要有强度折减法、超载法、刚体极限平衡法[1-4]、离散单元法(DEM)和有限单元法(FEM)等。其中,刚体极限平衡法是最常用的坝肩稳定分析方法,该方法概念明确、计算简单,有长期实践的经验,是一种可靠的概化分析方法。但由于坝肩岩体的复杂性,稳定性分析通常是建立在多种假设的基础上,因此,采用常规的刚体极限平衡法分析拱坝坝肩稳定存在一定的误差。
以锦屏一级高拱坝右岸坝肩为研究对象,结合三维非线性有限元分析结果,使用多重网格的方法,得到任一可能滑面(平面或曲面)上的应力分布与合力,从而分析滑面的稳定状态,并可求出与刚体极限平衡法类似的滑体安全系数。
1 坝肩稳定的刚体极限平衡法
对于一块山体而言,滑动体边界常常由若干个滑裂面和临空面组成。滑裂面一般为岩体内的各种结构面,尤其是软弱结构面,而临空面则为天然地表面。由于锦屏一级高拱坝右岸坝肩岩体质量较好,抗变形能力强,因此采用平面分层核算方法对其右岸坝肩稳定进行计算,为工程上的加固处理措施提供依据。刚体极限平衡法进行平面分层核算的步骤[4]如下:
取高度为1 m的水平拱圈及相应的拱座岩体作为计算对象,若滑裂体的滑裂面为铅直面,平面上的长度为,如图1(a)所示。由拱端及梁底传给滑裂体的力(包括法向力和剪力)分别为H、Va及G、Vb,其中G直接传给滑裂体底面,而H、V(即Va+Vb)传给铅直侧面AB。这样垂直于滑裂面的力N=Hsinθ-Vcosθ,而平行于AB面的力Q=Hcosθ+Vsinθ。考虑以上诸力后便可计算抗滑稳定安全系数K:
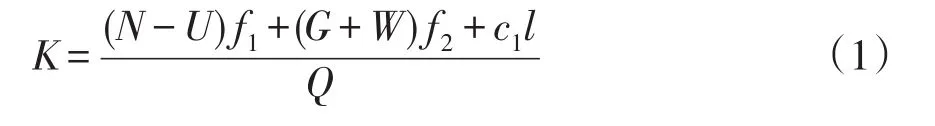
式中:K为考虑凝聚力c的抗滑稳定安全系数;f1、f2分别为沿滑动面AB、水平岩层的抗剪断摩擦系数;U为滑动面AB上的渗透压力,G为拱端面上的悬臂梁自重(宽度为1×tanϕ);W为拱座下游滑动岩体的重量,即图1(a)中的ABC(高度为1 m);c1为滑动面AB上的凝聚力强度;l为滑动面AB的长度。

图1 拱座稳定计算图Fig.1 Abutment stability calculation
2 坝肩滑块极限平衡的多重网格法
利用多重网格法分析坝肩稳定时,首先将可能滑面(平面或曲面)剖分成平面或曲面的网格;然后结合三维非线性有限元的分析结果,得到滑面上的应力分布与合力,从而分析滑面的稳定状态。
滑面上各节点的应力值由有限元应力结果插值得到,对于滑面上任一节点A,寻找包含节点A在内的坝肩岩体单元M,如图2所示,取单元M所有的高斯积分点对节点A进行插值。插值方法见式(2),假设单元均有8个高斯积分点:

式中,σij为滑面网格上任一节点A的应力,为单元M第k个高斯点的应力,S为单元M第kk个高斯点的权函数,Lk为节点A与第k个高斯点的距离[5]。
然后计算滑面网格各单元上的力矢量,先将四边形单元分成2个三角形单元,力的矢量和为2个三角形单元上力矢量的合成,如图3所示。三角形单元上的力矢量按下式计算:

图2 权函数示意图Fig.2 Diagram of weight function
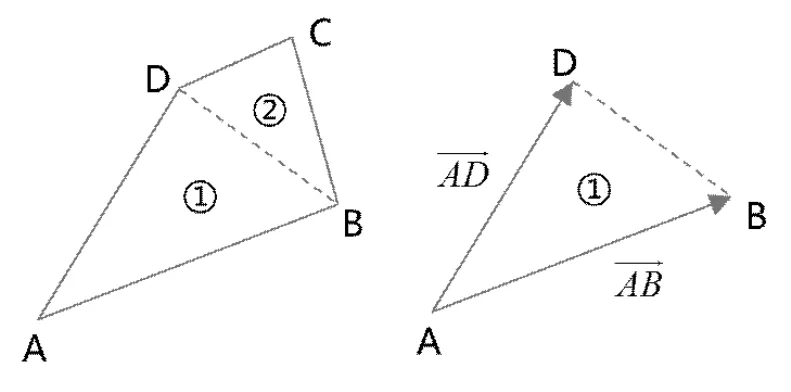
图3 面积矢量示意图Fig.3 Diagram of area vector

式中,Fi为某单元其中一个三角形单元上的力矢量;为该单元对应的三角形单元*节点应力;为该单元对应的三角形单元的面积矢量。
将滑面上各单元力矢量投影到单元面的法向和切向上,得到各单元上的阻滑力和滑动力。将所有单元叠加后,得到整个滑面上的阻滑力和滑动力,考虑滑动面凝聚力,进而确定块体稳定的整体安全度,如下式:

式中,f1、f2分别为沿滑动面AB、水平岩层的抗剪断摩擦系数;Fn表示滑动面单元上的法向力;Ft表示单元上的切向力;c为滑动面凝聚力强度;A为滑动面单元面积;M、N分别为滑动面AB、水平岩层滑动面上单元数量。
3 锦屏一级高拱坝坝肩稳定分析
3.1 工程地质概况
锦屏一级水电站位于四川省凉山彝族自治州盐源县、木里县交界的雅砻江干流,是雅砻江干流上水电开发的第一级。锦屏一级高拱坝为双曲拱坝,坝高305 m,正常蓄水位1 880 m,相应库容77.6亿m3,为大(1)型工程。
枢纽区地层岩性为三叠系中上统杂谷脑组砂板岩及大理岩。砂板岩分布于1 800 m以上左岸坝基及抗力体、边坡;大理岩分布于左岸坝基及抗力体、边坡约1 800 m高程以下和右岸整个坝基及抗力体、边坡;大坝坝址区出露煌斑岩脉有两条,呈平直延伸的脉状产出。坝址区主要断层发育包括左岸的f2、f5、f8、f42-9断层和右岸的f13、f14、f18断层等,左岸f2断层上下盘有2~4条层间挤压错动带集中成带分布,右岸层间挤压错动带共4条。这些软弱结构给坝肩的稳定带来了不利影响。枢纽区坝肩工程平面地质图如图4所示[6]。
3.2 三维模型网格及材料参数
锦屏一级混凝土双曲拱坝坝顶高程1 885 m,坝底高程1 580 m,坝顶厚16 m,拱冠梁底厚63 m。拱坝三维有限元网格采用八节点六面体和六节点五面体单元,节点总数145 812,单元总数135 973,其中坝体单元总数为4 232,共分为31层,三维整体有限元计算网格如图5所示。

图4 坝肩工程平面地质图Fig.4 Planar graph of abutment engineering geology

图5 锦屏一级高拱坝三维整体有限元计算网格Fig.5 3-D integrated finite element mesh of Jinping I high arch dam
模型考虑了离坝体较近的重要断层和控制性滑面,从右岸到左岸分别模拟了f13断层、f14断层、混凝土置换体、f5断层和f2断层,与坝体的位置关系如图6所示。

图6 断层和混凝土置换网格与坝体的位置关系Fig.6 The positional relationship among the fault,concrete re⁃placement grid and dam
采用D-P准则[7-9]作为材料的屈服准则,根据坝基岩体力学参数建议值,计算材料力学参数见表1。
3.3 计算方案
选取3种典型工况进行有限元分析,各工况下荷载组合如表2所示。
3.4 成果分析
应用多重网格法,计算得到三种不同工况下左、右岸坝肩不同高程的抗滑稳定安全系数K,如表3所示。

表1 材料力学参数表Table 1 Material mechanics parameters

表2 各计算工况的荷载组合Table 2 Loading combinations in each conditions
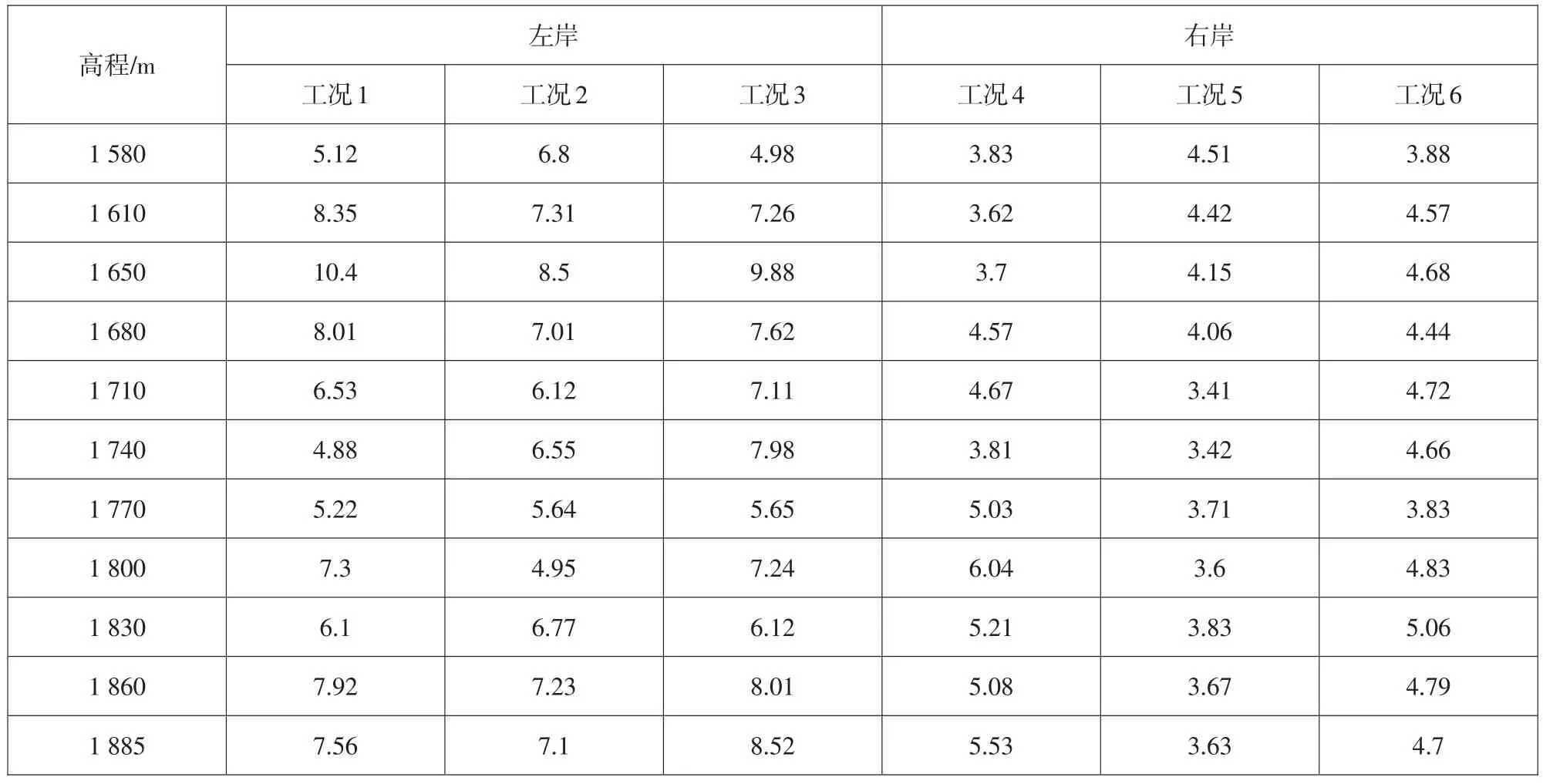
表3 左、右岸坝肩不同高程抗滑稳定安全系数Table 3 Anti-sliding stability safety factors at different elevations of left or right bank abutment
由计算结果可知:拱坝左岸坝肩的抗滑稳定安全度在基本组合工况(工况1、工况2)下,Kmin=4.88,出现在温降工况下的1 740 m高程;在特殊组合工况(工况3)下,Kmin=4.98,出现在校核洪水位工况下的1 580 m高程。拱坝右岸坝肩的抗滑稳定安全系数在基本组合工况下,Kmin=3.41,出现在温升工况下的1 710 m高程;在特殊组合工况(工况3)下,Kmin=3.83,出现在校核洪水位工况下的1 770 m高程。各工况下坝肩抗滑稳定安全度基本满足规范要求(基本组合K>3.5,特殊组合下K>3.0),在工况2时右岸坝肩局部抗滑稳定安全度稍有不足,需要对相应部位采取深部混凝土置换和断层防渗处理等补强加固措施。
4 结语
(1)结合锦屏一级工程,验证了多重网格方法进行坝肩稳定分析的可行性,计算简洁,概念清楚,有利于工程技术人员掌握和应用。
(2)利用多重网格法得到锦屏一级拱坝不同高程位置的坝肩稳定安全度。结果表明,工程右岸坝肩在温升组合工况下1 710 m高程部位的抗滑稳定安全系数不足,需进行相应的加固处理。
[1]DL/T 5346-2006,混凝土拱坝设计规范[S].
[2]SL 282-2003,混凝土拱坝设计规范[S].
[3]顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社,2006:166-167.
[4]沈长松,王世夏,林益才,等.水工建筑物[M].北京:中国水利水电出版社,2008:267-268.
[5]杨强,朱玲,翟明杰.基于三维非线性有限元的坝肩稳定刚体极限平衡法机理研究[J].岩石力学与工程学报,2005,24(19):3403-3409.
[6]宋胜武,向柏宇,杨静熙,等.锦屏一级水电站复杂地质条件下坝肩高陡边坡稳定性分析及其加固设计[J].岩石力学与工程学报,2010,19(3):442-458.
[7]杨强,陈新,周维坦.基于D-P准则的三维弹塑性有限元增量计算的有效算法[J].岩石力学与工程学报,2002,24(1):16-20.
[8]GU ChongShi,LI ZhanChao,XU Bo.Abnormality diagnosis of cracks in the concrete dam based on dynamical structure mutation[J].Science in China Series E:Technological Sci⁃ences,2011,54(7):1930-1939.
[9]顾冲时,吴中如.综论大坝原型反分析及其应用[J].中国工程科学,2001,3(8):76-81.
