基于径向基神经网络的重力坝损伤识别研究

吕 玮，高建勇，宋国良

（中国水利水电科学研究院，北京，100048）

0 引言

与世界上其他事物一样，重力坝也存在寿命问题。一般来说重力坝可安全运行100多年，但运行期内重力坝也会出现老化问题。遭遇地震时，大坝可能会出现震损，影响安全运行。近年来发展起来的损伤识别技术是一门综合性的应用科学，国内外的研究非常活跃。在理论方面进行了深入探讨，开发了诸如逆摄动法、微分方程反问题方法、传递函数法、脉冲函数法、频域相应法、推广卡尔曼滤波法等。上述这些方法已广泛应用于航天航空、造船、机械设备的故障预报及实时运行分析，其特点是利用某个振动特性或模式识别，对飞船、飞机或正在运转的机械进行在线故障监测，目前已在生产实践中发挥着越来越大的作用。在结构工程领域，机械阻抗法、波速法也已较成功地应用于桩基质量检测。用振动参数识别技术对混凝土框架进行破损评估（Damage Assessment by Dynamic Method），选用“残余力向量”识别结构的损伤部位，然后根据振动理论中的加权灵敏分析的方法识别结构的物理参数，由此来识别结构的损伤严重程度，目前已取得成效。近年来许多研究者在土木工程领域的动力诊断方面做了不少工作。瞿伟廉等[1]将神经网络方法应用于多层及高层框架结构的地震损伤诊断。姜绍飞等[2]采用一种自适应的概率神经网络对大跨悬索桥损伤定位进行研究，损伤识别效果明显优于传统概率神经网络。翁光远等[3]选用改进型BP神经网络，通过理论分析和模拟试验对悬臂板进行损伤识别，取得了良好的损伤检测效果，得出了结构损伤前后关于固有频率在不同损伤位置、不同损伤程度的变化规律。孙宗光等[4]以汲水门斜拉桥为例，对应用神经网络的模式分类技术识别桥梁结构损伤位置的方法进行了研究，输出结果以0～1的输出值表示损伤程度大小。在结构损伤状态未知，难以获得与损伤状况对应的响应时，Masri等[5]选用时程数据作为网络输入参数克服了这个难题。

损伤识别技术在混凝土大坝上的应用目前还少见报道，主要原因是大坝的老化、损伤对动态参数的敏感度低于机械故障诊断中动态参数的敏感度，因此对测试技术和分析水平的要求高很多。大坝动力诊断的许多问题涉及非线性变化，各变量之间关系复杂，多数工程实际问题难以用确切的数学、力学模型来解决。神经网络的非线性映射能力强，广泛应用于数据分类和非线性模式识别，能够滤出噪声或在有噪声情况下正确识别大坝结构损伤。利用大坝结构的特征物理量（固有频率、模态振型等）作为输入参数，以结构的损伤信息作为输出参数，通过一定数量的训练样本建立从输入参数到输出参数之间的映射关系，从而对结构的损伤进行识别和评估[6-7]。神经网络方法不但具有处理数据的能力，且具备对知识的学习和记忆能力，该方法成功应用于结构工程问题研究中，如多层及高层框架结构、大型桥梁结构、地下隧道、海洋平台等方向。

大坝结构发生损伤其动力特性也会随之改变[8]，已有研究表明基于结构动力特性的神经网络损伤识别适用于结构的地震损伤诊断[1]。在大型水利工程结构方面，王柏生等[8]验证了混凝土大坝结构损伤检测振动法是可行的，在有一定噪声干扰的情况下，神经网络方法仍可以准确识别出大坝损伤位置。赵琛[9]比较了不同噪声水平下的识别结果，证实概率神经网络方法应用于混凝土拱坝的损伤位置识别有一定的容错性。闫滨[10]证实RBF神经网络具有泛化能力强、预测精度高、训练速度快等特点，利用该方法对大坝进行安全评估，相比于其他神经网络具有明显优势。

1 径向基神经网络

径向基神经网络是基于函数逼近理论，由输入层、隐含层和输出层构成的一种三层前馈网络的结构。输入层包含的节点个数与输入向量x的维数相同，将输入单元信息传递到隐含层；隐含层的每个隐含节点对应一个训练数据点，输出层包含若干个线性单元，每个线性单元与所有隐含节点相连接，其网络结构如图1所示。

图1 RBF神经网络结构Fig.1 Structure of RBF neural network

径向基神经网络方法具备结构简易、训练方便、快速收敛、不容易陷入局部最小、能够逼近任何非线性函数、抗干扰能力强等特点[11]。在学习效率、分类能力上，径向基神经网络相比较于其他方法，具有非常明显的优势，因而被广泛应用于各科学领域中。

函数newrbe中spread表示径向基函数的扩散速度，它的取值针对具体情况做出相应调整。对于变化快的函数，若spread取值偏大可能使函数过于粗糙，逼近结果的速度过快，无法模拟真实映射；对于变化缓的函数，spread取值偏小可能使函数不够光滑，造成过学习，降低了推广能力[12]。

笔者在振动参数识别技术的基础上对其进行损伤诊断，利用神经网络所具有的特性，设计一个严格的径向基神经网络，输入参数选用结构的特征物理量，输出参数则是结构具体损伤信息，选定合适的训练样本建立输入参数与输出参数之间的映射关系，将用于测试的特征量送入训练好的网络中进行辨识，所得输出参数即对应结构的损伤状态信息，将得到的输出值与理想输出进行对比，分析损伤识别效果，从而判断方法是否有效。

2 损伤识别的两步诊断法

当大型复杂结构的某处发生损伤时，带来的影响难以被及时发现，常规的一步直接诊断方法对于简单结构非常有效，但对于复杂结构，因其动力自由度数目大、获取的测试数据不完备，直接采用常规方法诊断损伤十分困难。

针对以上问题，已有学者提出了结构基于神经网络技术的两步诊断方法。其中Kim[13]提出在有限测试信息情况下的损伤诊断法，先采用模型修正大致判断损伤位置，后分析结构损伤敏感性得到具体损伤信息。李国强等[14]提出对框架结构损伤进行两步诊断，先利用动力模态识别结构刚度矩阵，再使用单纯形法识别损伤。瞿伟廉[15]等提出高层复杂框架结构的两步损伤诊断法，先定位损伤子区域，再针对该区域进行具体诊断。

在已有研究的基础上，笔者提出适用于大型水利工程结构损伤的两步诊断方法，基本思路为：在损伤识别的过程中，第一步大致判断损伤所在区域，第二步细分该区域重新建立样本集和映射关系，进行具体损伤诊断。基于振动参数识别技术对大坝进行损伤检测，选用径向基函数神经网络对重力坝进行损伤识别，从理论层面研讨、数值模拟验证、模型试验验证几方面展开研究。

3 算例分析

武都水利工程主体工程武都大坝为碾压混凝土重力坝，试验中选取19号右岸非溢流坝段进行研究，将模型结构进行简化。假定坝体材料为弹性体，建立武都大坝19号坝段缩尺模型，满足模型与原型之间弹性相似，采用修正的Westergaard公式将动水压力转为附加质量加在坝体上游面。

武都大坝模型在振动台试验中空库、满库以及每次激励后都用白噪声扫频，验证模型是否具有缺陷，测定各个激励试验后模型结构的动力特性。模型经过1.8倍设计地震激振，结构固有频率降低，刚度明显下降，坝体颈部表面出现细微裂缝，对此状态下的模型进行损伤识别。

3.1 数值模拟损伤识别

裂缝是大坝最常见的损伤之一，强地震作用下，靠近坝顶的坝体突变处容易发生横向扩展，甚至出现贯穿坝体上下游的水平裂缝。根据振动台试验结果和以往震害资料[16]，大致确定大坝震后易出现损伤的区域主要集中在靠近坝顶部位，尤其是坝体断面发生突变处。鉴于结构的微小损伤难以有效识别，裂缝开裂时对坝体刚度的影响较大，笔者采用坝体上部的水平向裂缝来模拟损伤。

图2 武都大坝19号坝段模型Fig.2 The model of section No.19 of Wudu dam

图3 武都大坝的二维有限元模型Fig.3 2-D finite element model of Wudu dam

根据武都大坝试验模型相关信息，利用ABAQUS有限元软件建立二维有限元模型，将大坝震后易损伤的位置划分为多个区域，获得不同损伤情况下结构的动力特征。神经网络损伤识别关键在于容易测得且对结构损伤有足够敏感性的输入参数，选取不同的结构特征量作为输入参数对输出结果的影响不同[17]。对于非对称结构，固有频率能反映结构整体的动力特性，最容易得到且具有很好的识别精度。选用固有频率和固定点的模态分量组合作为输入参数来训练网络，受模型误差影响较小且识别效果好[18]。

算例中选取结构固有频率和固定点的第一阶模态水平分量作为输入参数，损伤状态作为输出参数，建立训练样本集。为研究模型试验获取的测试数据不完备，验证输入参数减少时该方法的有效性，将输入参数分为两组进行对比。数据完备组选用结构的前十阶固有频率和五个固定点的第一阶模态水平分量作为输入参数，数据不完备组选用结构的第一阶固有频率和三个固定点的第一阶振型水平分量作为输入参数，分别建立训练样本，对结构进行损伤诊断。

3.2 损伤程度识别

在坝颈段的上游面和下游面，距坝顶2/19、3/19、4/19、5/19坝高处模拟水平裂缝，上游面用大写字母ABCD表示，下游面用小写字母abcd表示，每处的裂缝分为5种损伤程度，分别为该处坝体截面宽度的0.2、0.4、0.5、0.6、0.8倍，共得到41组训练样本。神经网络理想输出参数为（ya,yb,yc,yd），yx表示结构在x的损伤量。例如（0,0,-0.5,0）表示结构在下游面c处的损伤程度为0.5。

对于损伤位置已在确定范围内的情况，选取四组样本用来测试该方法对于损伤程度的识别精度。

结果如表1所示，结果表明远离损伤位置接近于0，神经网络具有数据分类特性，能准确区分出损伤位置。当测试样本的损伤位置与训练样本重复或极为靠近时，该方法能进行损伤程度识别，具有良好的精度。

在数据不完备的情况下，神经网络识别损伤的精度有所下降。当结构损伤程度小时，识别大致损伤位置；当结构损伤程度大时，该方法仍具有数据分类特性，能准确识别损伤位置，但对于损伤程度的识别误差较大。

3.3 损伤位置识别

对于损伤位置未知的情况，选取两组样本用来测试适用于大型水利工程结构损伤的两步诊断方法对于损伤位置的识别精度。

用训练好的样本集初步定位损伤，从结果上看，测试样本损伤的位置介于两种训练样本之间，远离损伤位置输出结果接近于0，该方法能对损伤位置进行初步定位识别。

再次定位损伤，根据前一次识别结果将损伤发生的大致范围进行细分，把B、C两个位置平均分为三段，在B'、C'处分别增加两条裂缝，每处的裂缝长度分为5种损伤程度，分别为该处坝体截面宽度的0.2、0.4、0.5、0.6、0.8倍，共得到61组训练样本。神经网络理想输出参数为（ya,yb,yb',yc',yc,yd），yx表示结构在x的损伤量。例如（0,0,0,0.5,0,0）表示结构在C'处的损伤程度为0.5，两次识别结果如表2所示。

表1 神经网络输出与测试样本比照Table 1 Comparison of neural network output and test samples

可以看出，该方法可以识别出损伤的大致范围，以便下一步更加准确地识别其损伤程度。

3.4 模型试验损伤识别

用模型试验检验该方法进行损伤识别时的有效性。根据模型结构试验后发生损伤后的实测模态参数，选取第一阶固有频率和三个固定点的第一阶振型水平分量作为输入参数，代入训练好的神经网络，所得结果如表3所示。

从计算结果可以得出两步诊断方法进一步确定损伤位置在模型试验中的有效性。对比模拟数据所得结果与实测数据所得结果，前者明显优于后者。理论上振型的变化对损伤更为敏感，但实测中难以得到结构完备的损伤信息，这样所得的结构振型与真实情况有一定偏差，裂缝并不是完全水平延展，这使得神经网络输出结果精度降低。

图4 模型坝体侧面裂缝Fig.4 Cracks at the side of model

基于径向基函数神经网络分析结果能区分出损伤位置在上游面裂缝C附近，裂缝C距坝顶4/19坝高处，为模型高度673 mm附近，测试结果与试验的一条位于700 mm附近裂缝的位置基本吻合。

表2 神经网络输出与测试样本比照Table 2 Comparison of neural network output and test samples

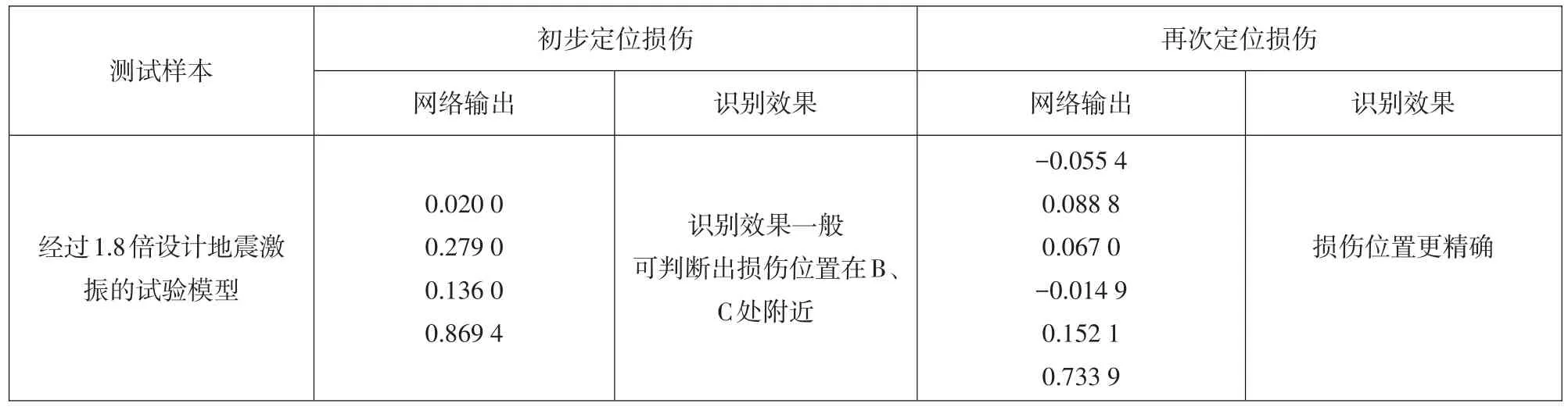
表3 模型试验损伤识别结果Table 3 The results of the damage identification

4 结语

（1）基于径向基函数神经网络的结构损伤识别方法可以用于大型水利工程结构损伤位置识别、损伤程度的预测。两步诊断法能将损伤发生范围逐步缩小，较为准确地识别其损伤程度，特别是对于单一位置的损伤程度和定位有良好的识别效果。针对实际问题中所得的模态信息不完备的情况，该方法仍具有一定识别精度。

（2）径向基函数神经网络模型具有联想和泛化能力，用于损伤识别虽有良好的精度，但也存在局限性，选择训练样本时要将损伤情况尽可能包含在内，否则神经网络的识别能力会有所下降。对比同一损伤位置的损伤程度不同的情况，损伤程度大时，识别精度高。如何结合现有的研究成果，考虑在振动实测工作中选取更容易得到、识别精度高、对结构损伤敏感性高的参数，还需要进一步深入研究。

（3）基于现有监测方法，难以发现大型结构中的微小裂缝，若能在裂缝发展初期识别损伤信息，消除有可能存在的安全隐患，将极具意义。神经网络方法用于重力坝损伤识别是一个很有潜力的研究课题，有待在实际问题中检验和改善。

[1]瞿伟廉,陈伟.多层及高层框架结构地震损伤诊断的神经网络方法[J].地震工程与工程振动，2002,22(1):43-48.

[2]姜绍飞,刘明,倪一清,高赞明.大跨悬索桥损伤定位的自适应概率神经网络研究[J].土木工程学报,2003,36(8):74-78.

[3]翁光远,王社良.基于BP神经网络的结构损伤识别方法研究[J].华中科技大学学报:城市科学版,2009,26(2):16-18.

[4]孙宗光,高赞明,倪一清.基于神经网络的损伤构件及损伤程度识别[J].工程力学,2006,23(2):18-22.

[5]Masri S F,Smyth A W,Chassiakos A G.Application of neu⁃ral networks for detection of changes in nonlinear systems[J].Joumal of Engineering Mechanics,2000,126(7):666-676.

[6]姜绍飞.基于神经网络的结构优化与损伤检测[M].北京：科学出版社,2002.

[7]朱宏平.结构损伤检测的智能方法[M].北京：人民交通出版社,2009.

[8]王柏生,何宗成,赵琛.混凝土大坝结构损伤检测振动法的可行性[J].建筑科学与工程学报,2005,22(2):51-56.

[9]赵琛.用概率神经网络对混凝土拱坝进行损伤位置识别的研究[D].浙江大学,2005.

[10]闫滨.大坝安全监控及评价的智能神经网络模型研究[D].2006.

[11]Samarasinghe S.Neural Networks for Applied Sciences and Engineering:from Fundamentals to Complex Pattern Recognition[M].New York,USA:Taylor&Francis,Inc,2007.

[12]陈明.MATLAB神经网络原理与实例精解[M].北京：清华大学出版社,2013.

[13]Kim H M,Bartkowicz T J.A Two-Step Structural Damage Detection Approach With Limited Instrumentation[J].Journal of Vibration&Acoustics,1997,119(2):258-264.

[14]李国强,郝坤超,陆烨.框架结构损伤识别的两步法[J].同济大学学报,1998,26(5):483-487.

[15]瞿伟廉,陈伟,李秋胜.基于神经网络技术的复杂框架结构节点损伤的两步诊断法[J].土木工程学报,2003,36(5):37-45.

[16]陈厚群.混凝土高坝强震震例分析和启迪[J].水利学报,2009,40(1):10-18

[17]朱宏平,余璟,张俊兵.结构损伤动力检测与健康监测研究现状与展望[J].工程力学,2011,28(2):1-11.

[18]王柏生,倪一清.框架结构连接损伤识别神经网络输入参数的确定[J].振动工程学报,2000,13(1):137-142.