刚挠结合印制板中埋入挠性基板区尺寸研究

王守绪 周国云 董颖韬 何 为（电子科技大学微电子与固体电子学院，四川 成都 610054）胡永栓 苏新虹（珠海方正科技高密电子有限公司，广东 珠海 519170）

刚挠结合印制板中埋入挠性基板区尺寸研究

王守绪 周国云 董颖韬 何 为
（电子科技大学微电子与固体电子学院，四川 成都 610054）
胡永栓 苏新虹
（珠海方正科技高密电子有限公司，广东 珠海 519170）

研究了刚挠结合印制板中挠性区埋入尺寸dE、刚挠互连盲孔距刚挠结合边缘尺寸dH、及该类印制板的挠曲次数Y等之间的关系，获得的拟合方程式为：Y＝-34.2＋22.7dE＋16.3dH。实验结果表明，dE＝2.0cm，dH＝1.8cm是满足6层刚挠结合印制板弯折4000次数挠曲性要求的最小临界参数。

刚挠结合印制电路板；挠曲能力

1 前言

有一种刚挠结合印制电路板（R-FPCB）的设计是挠性埋入区域尺寸较少，使用盲孔实现刚挠区域上下层互联[1]-[3]。如图1所示，挠性埋入尺寸dE和刚挠互连盲孔距刚挠结合边缘尺寸dH的大小决定着R-FPCB的机械性能和电气性能。目前未见业界有对以上两尺寸作出相关研究和标准规定，但是良好的挠性埋入尺寸dE和刚挠互连盲孔距刚挠结合边缘尺寸dH极大地影响到R-FPCB的品质。

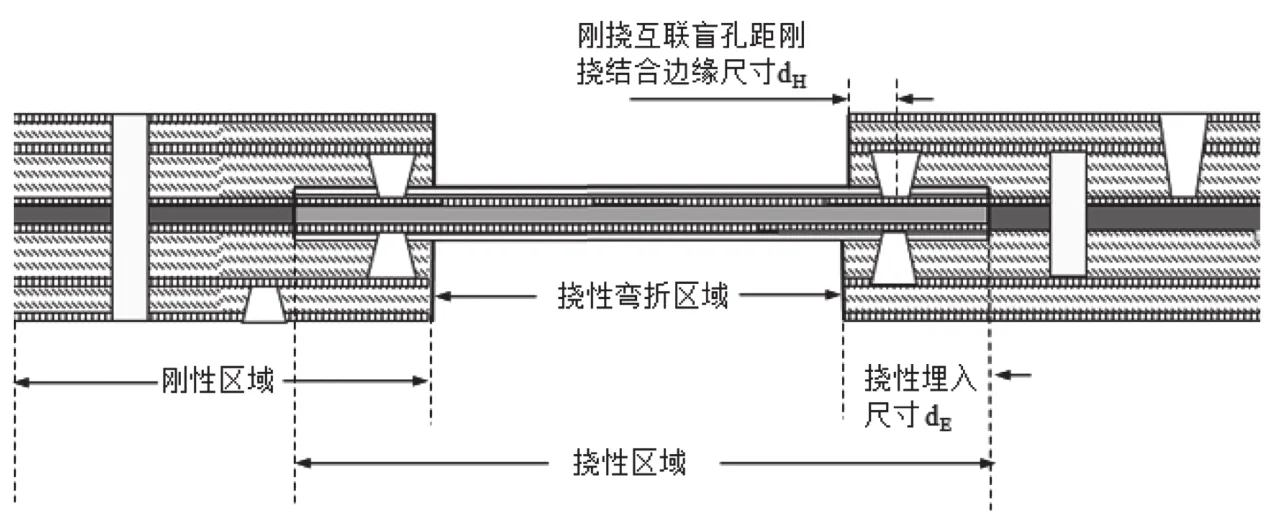
图1 R-FPCB的结构图

R-FPCB在弯折过程中，刚挠结合处挠性区基板上、下两面交替承受弯折压力和拉力，如图2所示。R-FPCB的刚挠结合处的应力承受能力成为挠曲性能的决定因素。弯折时结合部受到弯折压力一面方向指向刚性基材内部；而另一侧则指向刚性基材外部。如果将两作用力分解为垂直和平行于印制板表面的两个分力就可发现，沿刚挠结合处垂直剖面的两个力分量大小相等，方向相反，作用在一条直线上彼此抵消，两力的相互作用下形成对挠性基材的微小挤压，影响较小；而垂直于刚挠结合处垂直剖面（平行于印制板表面）的两个力分量大小也是大小相等、方向相反，但彼此平行并不能彼此抵消，成为R-FPCB弯曲作用下挠性埋入区域成平行四边形变形扭曲并最终脱离刚性板材夹层的原因。

从理论上扩大挠性区埋入尺寸可与弯折内应力抗衡，实现弯折区域的机械稳定性，而尺寸过大，会丧失这种R-FPCB的特殊性，与传统刚挠结合印制电路板无异。因此，这种板设计与制造时必须考虑以下因素：首先，挠性埋入尺寸dE。埋入尺寸太小，弯折性达不到可靠性标准，且制作困难，容易造成挠性区脱落和结合处开裂等机械性能不良现象、后续工序的化学药水渗入等造成电气不良；埋入尺寸太大，造成挠性板材的浪费，和挠性单元涨缩较大等缺陷[4]。其次，刚挠互联盲孔距刚挠结合边缘尺寸dH。其距离较大同样不能体现高密度互连特性，造成挠性基材的浪费[5]；但距离太小，容易因弯折应力影响到盲孔的电气性能，造成刚挠互连失效，可靠性降低。本文研究了dE和dH对PCB挠曲性影响规律，为这种R-FPCB设计和制造提供指引。

2 试验部分

2.1 实验材料及设备

无胶压延型聚酰亚胺覆铜双面（12 μm/20 μm/ 12 μm），覆盖膜（聚酰亚胺/丙烯酸粘结剂 15 μm/ 12.5 μm），FR-4覆铜双面板（铜箔/FR4/铜箔 12 μm/ 150 μm/12 μm），半固化片（106 RC67% 55 μm±5 μm），挠曲性测试仪（型号XD-6306A），微电阻测试仪（型号HIOKI-3540）。

2.2 埋嵌挠性线路印制电路板挠曲性性能研究

按全流程制作6层R-FPCB作为测试板，6层板为芯板3/4层嵌入挠性线路，2/5层为网格铜面并有盲孔连接内层挠性芯板，1/6层设计有测试点。根据实验经验，测试板中挠性埋入尺寸dE分别选取为2.5 mm、2.0 mm、1.5 mm，在每一个dE尺寸下，设计刚挠互联盲孔距刚挠结合边缘尺寸dH分别为1.5 mm、1.0 mm、0.5 mm。使用微电阻测试仪测试设计测试点的电阻，判断挠性线路的导通性。挠曲性测试的参数为挠曲速度50次/min，挠曲角度135°，挠曲半径2.5 cm，如图2所示。每2分钟使用微电阻测试仪测试电路导通情况，即以每弯折100次为基本单位，不足100次计为0，超过100不足200计为100，电路不通时即停止。试验结果评价是以挠性次数Y为标准，试验数据与测试结果如表1。测试样板使用相同的压合工艺等以消除相关因素的影响。

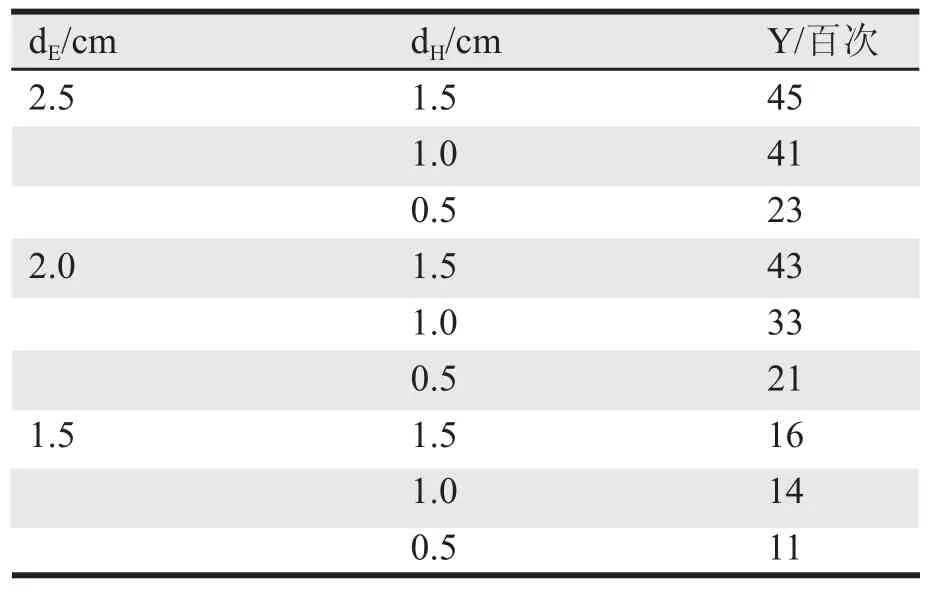
表1 dE/dH实验设计与结果

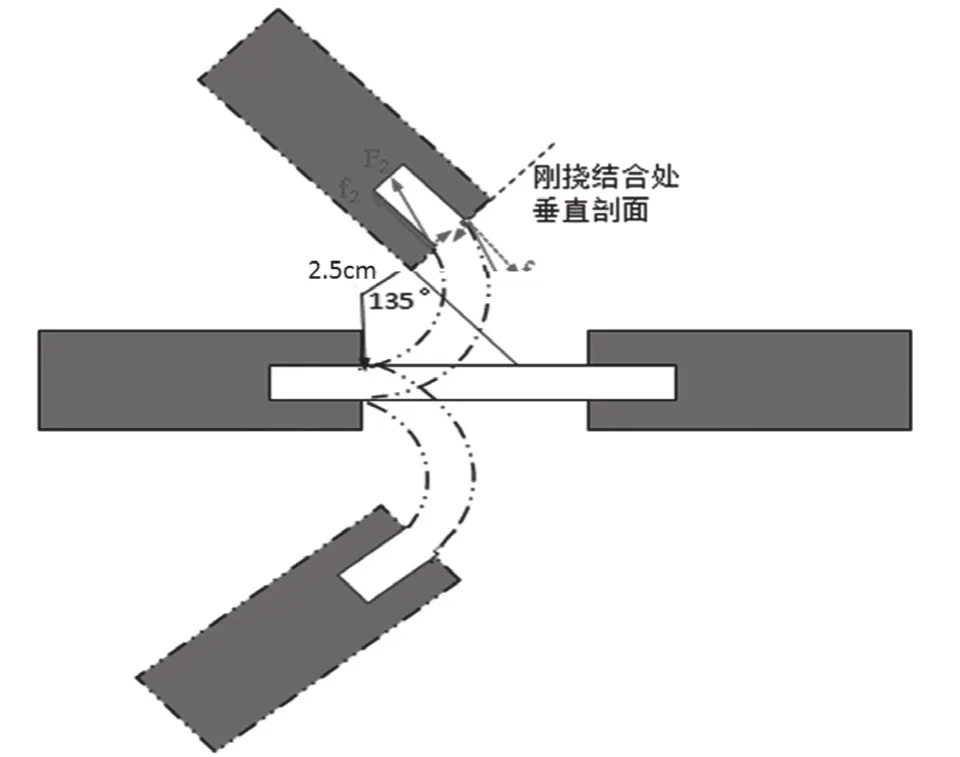
图2 R-FPCB刚挠结合处应力分析与挠曲性测试示意

2.3 R-FPCB埋入挠性区尺寸研究

设计6层测试板，如图3所示，挠性线路埋入尺寸dE为2.0 cm，刚挠互联盲孔距刚挠结合边缘尺寸dH为1.8 cm。对测试板做挠曲性测试，记录弯折次数，并做金相切片观察4000次弯折测试后的刚挠结合处剖面图。如图4所示，4000次挠曲测试后的挠性介质和刚性介质结合紧密未出现开裂、变形的机械性能故障，盲孔内电镀层与介质层结合紧密，电气性能良好。

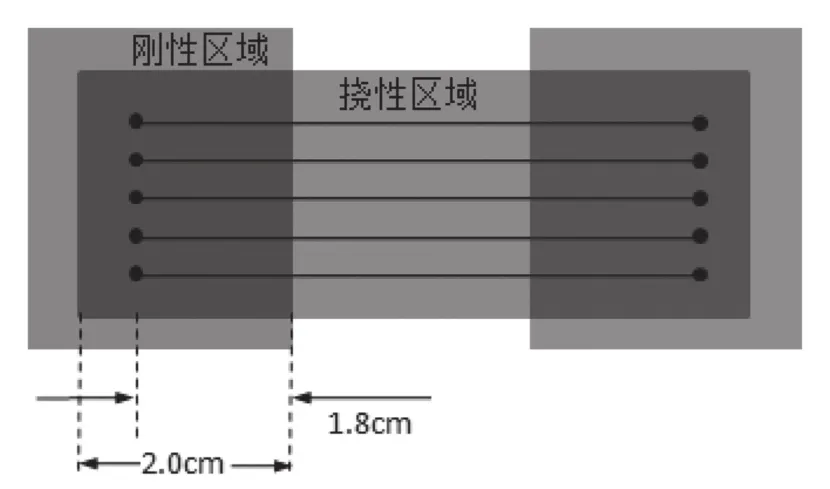
图3 挠曲性测试板

图4 4000次弯折测试后的刚挠结合处剖面

为准确观察和记录测试板的挠性弯曲次数，在接近4000次挠曲时，使用微电阻测试仪加大抽检率，准确记录测试板所承受的最大挠曲次数，记录30组数据，并对弯折次数过程能力分析。实验数据及分析如图5所示。

图5 R-FPCB测试板的弯折次数过程能力

3 实验结果及分析

将表1中的数据用origin 8.0数据处理软件进行作图，所得结果如图6所示。从3组曲线中可以直观看出：固定挠性线路埋入尺寸dE值，其挠性弯折次数Y随着刚挠互连盲孔距刚挠结合边缘尺寸dH的增大而增大；同理，固定dH值，Y值随着dE的增大而增大；综合体现了刚挠结合处的尺寸越大，盲孔位置越深，其刚挠结合性能越好，这也是传统刚挠结合板的优势。另外，也可直接看出，在dE为1.5 cm时，所测各dH下的弯折次数远远小于dE为2.0 cm、2.5 cm的弯折次数，而dE为2.0 cm、2.5 cm时，结果趋于平缓，即dE在1.5 cm与2.0 cm之间存在拐点；dE为2.0 cm、2.5 cm时，各dH值下的弯折次数Y差异不大，尤其是dH值1.5 cm时，弯折次数Y几乎一致，表明dE大于2.0 cm时，这种R-FPCB的挠曲性能已经趋于稳定的可靠性，具有和传统刚挠结合板一样的机械和电气稳定性。弯折次数总体的上升次数，表明了Y与dE、dH具有一定线性关系，利用origin 8.0数据处理软件对所得各参数和数据进行多项式拟合，拟合方程为：

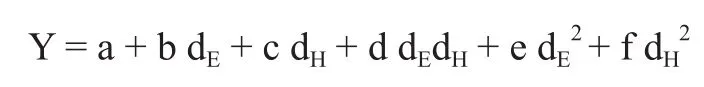
对于拟合结果，进行回归分析和变量筛选，根据统计量的显著水平对显著性较小的变量进行淘汰。最后得到置信度与相关度都较高的线性回归方程：

方差分析拟合曲线的各参数对结果是否有显著性影响，结果如表2所示。F检验值表明，挠性线路埋入尺寸dE和刚挠互连盲孔距刚挠结合边缘尺寸dH对其挠性弯折次数Y具有高度显著性，且dE显著性要高于dH，其它二次项因子误差忽略。

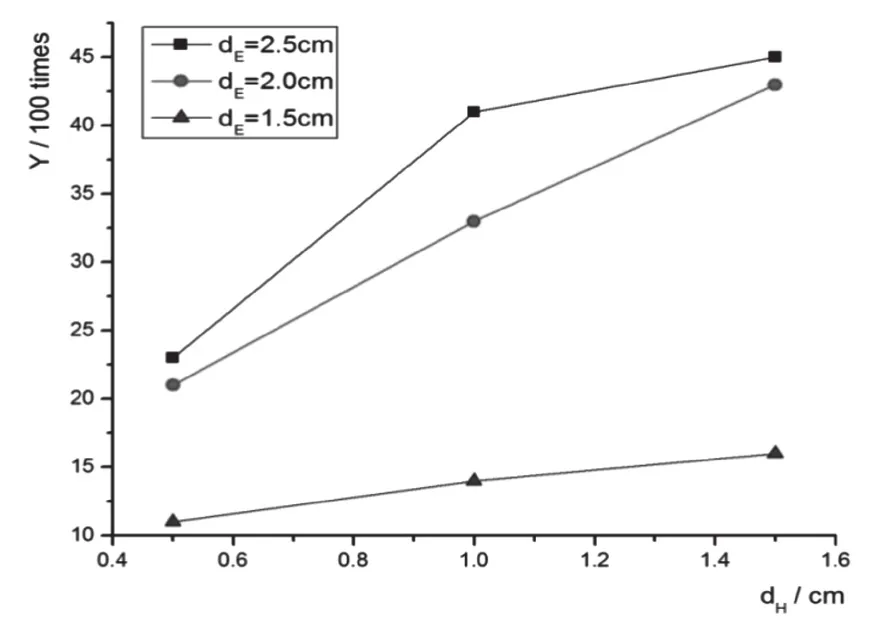
图6 dE/dH对弯折次数Y的影响关系

表2 拟合曲线方程的各因素方差分析

综合以上分析得到：（1）dE在1.5 cm与2.0 cm之间存在拐点；（2）dH为1.5，dE为2.0 cm时，弯折结果差异并不大；（3）dE显著性远要高于dH；（4）根据实验经验，弯折次数4000次以上，才能满足实际应用。所以选取Y值为40，dE取值为1.5 cm、1.6 cm、1.7 cm、1.8 cm、2.0 cm，求取dH值。结果如表3所示，满足条件的参数为dE=2.0 cm，dH=1.8 cm，此参数是满足6层E-flex在测试条件的挠曲性测试的最小临界参数。

从图6可知，在最优条件小，即以dE为2.0 cm和dH为1.8 cm的设计标准制作的测试版，其整体能力的统计量CPK为1.65大于1.33，且都超过基本次数4000次。

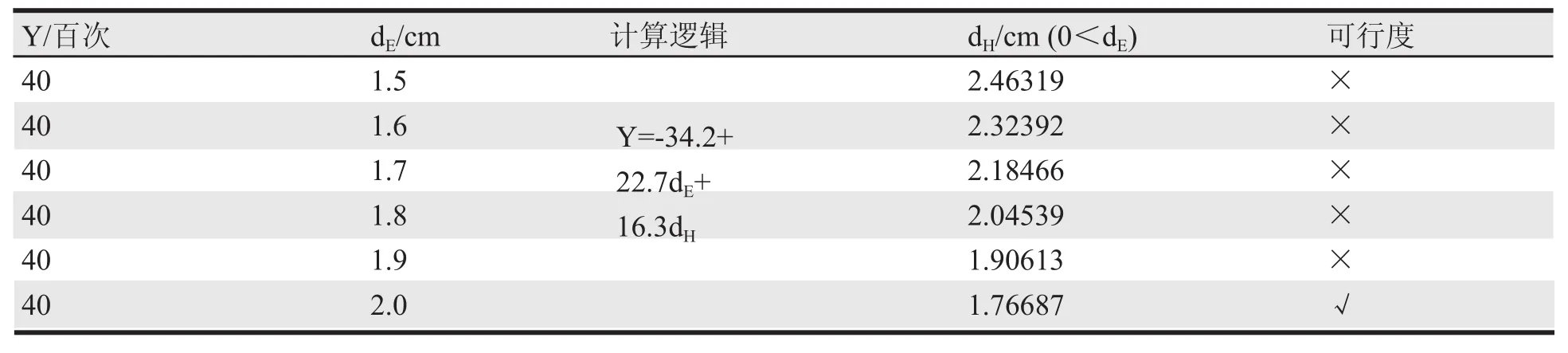
表3 d/d的最优参数计算

4 结论

R-FPCB的挠性区埋入尺寸dE、刚挠互连盲孔距刚挠结合边缘尺寸dH、及该类印制板的挠曲次数Y之间存在相互关系，其拟合方程为，Y=-34.2+22.7dE+16.3dH。对于六层R-FPCB的挠性区为聚酰亚胺基板、刚性区为FR-4基板时，其埋入挠性基板的尺寸设计可按照参数dE=2.0 cm，dH=1.8 cm完成，此组参数具有良好的过程控制能力，其弯曲次数在4000次以上。

[1]张怀武,何为等. 现代印制电路原理与工艺[M]. 北京:机械工艺出版社,2010,10-15.

[2]张星龙. 刚挠结合PCB设计技术[J].电讯技术, 2003,43(4):114-117.

[3]黄勇,胡永栓等. 挠性板部分埋入制作刚挠结合板[J]. 电子元件与材料,2012,31(8):53-54.

[4]De. Jong, J.A. Ferreira, P. Bauer. 3D Integration with PCB Technology[C]. Applied Power Electronics Conference and Exposition, USA,2006,857-863.

[5]刘建生,何润宏等. 半挠性印制电路板的制造方法[P]. 中国:发明专利,CN101365298A.

王守绪，电子科技大学副教授，从事先进印制电路板制造材料及技术研究工作。论文工作获得了广东省2013年重大专项的资助（项目编号：2013A090100005）。

Research on area size of embedded flexible substrate in R-FPC

WANG Shou-xu ZHOU Gou-yun DONG Yin-tao HE Wei HU Yong-shuan SU Xin-hong

The paper studied the R-FPCB embedded dimension dE, the dimension of blind hole to the R-flex edge dH, and the number of deflection Y in R-FPCB. The fitted equation is:Y＝-34.2＋22.7dE＋16.3dH. The experimental results showed that the minimum critical parameters that meet the deflection request of bending 4000 times were dE＝2.0cm, dH＝1.8cm in 6 layer R-FPCB.

R-FPCB; Flexural Capacity

TN41

A

1009-0096（2015）05-0018-04