基于K-均值聚类的协同进化粒子群优化算法

王燕燕 ，葛洪伟 ，杨金龙 ，王娟娟

1.江南大学 物联网工程学院，江苏 无锡 214122

2.国网潍坊供电公司，山东 潍坊 261021

粒子群优化（P article Swarm Optimization，PSO）算法[1]是一种基于种群的智能优化算法，该算法具有可变参数少，且简单易于实现的特点，得到了广泛关注。为了避免粒子陷入局部最优，提高粒子的全局搜索能力，增加算法的应用领域，研究者常将其与其他的智能优化算法相结合研究，以期达到更加好的优化能力[2-3]。文献[4]引入了惯性权重，加快了算法的收敛速度。文献[5]通过引入时变加速因子和时变惯性权因子，有效地增强了算法的局部搜索能力。文献[6]提出的多种群多模型协同进化的粒子群优化算法，有效地提高了种群的多样性。

这些算法随着维数增加会出现优化性能迅速恶化的现象，而许多现实问题中需要解决的往往都是高维（几十维以上，本文在100维上进行实验）优化的情况[7-9]。为了解决高维优化问题，Potter和Jong[10]等提出协同进化（cooperative co-evolutionary，CC）框架，将种群分解成多个单独的子种群（每个子种群的搜索范围较低），为解决高维问题提供了一个很有前途的方法。文献[11]将协同进化框架[10]引入到PSO算法中，通过CC框架对粒子群进行分组，提出协同粒子群优化（Cooperative Particle Swarm Optimization，CPSO）算法：CPSO-SK和CPSO-HK算法，该算法通过降低种群的搜索范围，增加函数评价次数的处理方法，有效地提高了PSO算法处理高维优化问题的收敛速度。文献[12]在每一次迭代中对各分量进行自适应加权，避免了各分量相互依赖度很大而导致算法的性能恶化。文献[13-14]提出的协同进化粒子群优化（CCPSO2）算法采用动态分解和重组变量的方法，避免了交互粒子划分到不同群中，提高了算法处理高维问题的优化性能。现有的这些处理高维优化问题的算法[10-14]，在一定程度上提高了算法处理高维优化问题的性能，但是存在着收敛速度慢、优化性能不佳的问题。

针对上述算法解决高维优化问题的缺陷，本文提出了一种基于K-均值聚类的协同进化粒子群优化（Cooperative Coevolving Particle Swarm Optimization based onK-means Cluster，KMS-CCPSO）算法，该算法采用K-均值算法对粒子群进行子种群划分，在保证粒子群的局部搜索和全局搜索能力的同时，也有效避免了粒子群算法易陷入局部最优的问题。

1 粒子群优化算法

PSO算法采用随机初始种群位置和速度，并通过迭代更新找到最优解。在迭代过程中，粒子通过两个极值更新位置和速度。一个极值是粒子本身所遍历得到的最优解，称之为个体最优解；另一个极值是整个种群到当前时刻所得到的最优解，称之为全局最优解。PSO算法的速度和位置的更新公式为：

2 协同进化粒子群优化算法

CPSO算法[11]是由CPSO-SK算法[11]和CPSO-HK算法[11]相结合得到的，采用指定子种群维数的分组策略对种群进行划分子空间，降低函数的搜索空间，有效地提高了算法的收敛速度。

CCPSO2算法[14]借鉴了CPSO算法[11]对种群划分子空间的思想，但不再预先指定子种群的规模，而是采用自适应方案动态决定子种群的规模的分组策略，提高了交互变量划分到相同子种群的概率，提高了算法的优化性能。交互变量划分到同一子种群的概率计算公式[14]为：

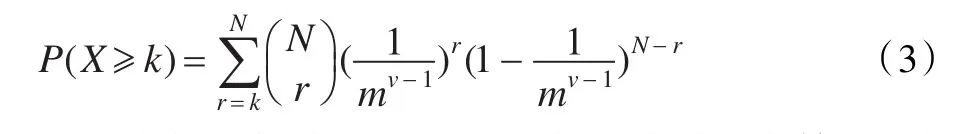
其中，X是交互变量划分到同一个子种群的次数；k是当前迭代次数；N是总迭代次数；r是当前迭代次数；的简写是从N个次数中取出r(r≤N)个次数的组合数。m是子种群数；v是交互变量总数。

由概率计算公式（3）可知，CCPOS2算法采用的动态分组策略提高了交互变量划分到同一子种群的概率。

分组策略[10]是处理高维问题最有效的方法。通过分组策略，将种群划分成多个子种群，各个子种群在不同的搜索范围内进行优化，整体上降低了种群的搜索范围，有效地提高了算法的收敛速度和优化性能。

3 K-均值算法

近年来，数据挖掘成为一个很热的研究方向，作为其主要方法之一的聚类也因此受到人们的关注。K-均值算法[15]是最早提出的较为经典的聚类算法之一，该算法鲁棒性较强，能够解决传统上难以解决的问题，已在诸多领域上得到了广泛的发展和应用。

K-均值算法[15]是一种基于划分方法的聚类算法，考虑了样本间的相似性度，该算法通过欧氏距离作为相似度测度，求对应某一初始聚类中心向量V的最优分类。样本间的欧氏距离越小，说明样本间的相似度越大，反之同理。根据欧氏距离的大小将给定的n个粒子划分成k个不同的簇，其簇内粒子具有较高的相似度，簇间粒子具有较低的相似度。

其中，i表示第i个簇；xj表示第j个粒子，j∈[1,n]；μi表示第i个簇的聚类中心。K-均值算法[15]步骤：将给定的n个粒子划分成k部分，每一部分称为一个簇。首先，随机地选取k个粒子，每个粒子作为一个簇的初始中心。对剩余的每个粒子，按照其与选定的各个簇的中心的距离，将它赋给与其距离最短的那个簇。然后计算每个簇内粒子的距离平均值，再将粒子与新的聚类中心进行距离比较，把粒子赋给与其最近的簇中。

图1中黑色圆点代表随机选取的聚类中心；灰色圆点代表更新后的聚类中心；弧线代表划分成两个区域。

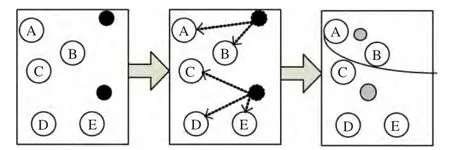
图1 k-means算法的计算过程

K-均值算法存在两个缺点：（1）对聚类中心的选取依赖性较大；（2）对聚类所在的维数空间的要求很高。综上可知，要想引入K-均值算法就必须解决K-均值算法的缺点。在本文中，k-均值的聚类中心是从粒子中随机选取的，好坏粒子被取出的概率均为50%，且无法确定当前好的粒子就一定能带领种群找到最优解，也不确定当前不好的粒子就一定不能找到最优解。所以这种随机选取的聚类中心会增加种群的多样性，避免种群陷入局部最优。随着进化的进行，所有粒子会向着一个地方运动，此时选出的聚类中心无论是否是随机取得的都不会影响最终结果。因此，本文将K-均值算法的聚类中心点与种群最优位置进行结合，避免K-均值算法对聚类中心的过渡依赖。而且，为了保证K-均值算法的良好性能，将子种群的搜索范围设定在二维空间中，有效地避免了K-均值算法随着维数的增加，算法的性能会逐渐变差的情况。

通过公式和分析可知，引入K-均值算法的粒子群优化算法后，在种群进化的初期子种群间的相似度较小，使得种群的搜索范围较大，保证种群的多样性，具有较强的全局搜索能力；在种群进化的后期，种群间的相似度较大，种群的搜索范围缩小，粒子只在趋于不变的聚类中心点附近的范围进行优化，具有较强的局部搜索能力，从而可以有效地避免了粒子群算法易陷入局部最优的问题。

4KMS-CCPSO算法

4.1 算法思想

由于分组策略可以有效地提高算法的收敛速度和优化性能，而K-均值算法可以有效地避免粒子群算法易陷入局部最优。因此，本文将分组策略和K-均值算法引入粒子群优化算法中，综合分组策略和K-均值算法优势，设定分组维数为二维，降低高维优化问题的搜索空间，提高算法的收敛速度，避免粒子陷入局部最优，从而使粒子群优化算法处理高维优化问题的性能得到提高。

4.2 算法步骤

为解决高维的优化问题，优化算法需要保持很好的搜索性和收敛性。KMS-CCPSO算法使用柯西和高斯分布相结合的公式[14]对粒子的位置进行更新，其中选取全局最优解和局部最优解的差值作为两大分布的标准差，公式为：

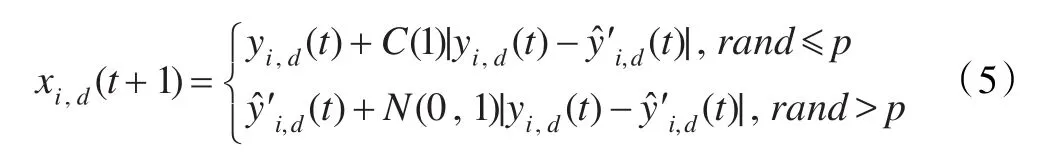
其中，yˆ′i,d(t)和yi,d(t)分别表示粒子i的局部最优解和个体最优解，C(1)表示标准柯西分布，N(0,1)表示标准高斯分布。

算法的步骤如下：

步骤1设置粒子群数目、维数、最大迭代次数、子空间维数以及K-均值算法的聚类中心数目。

步骤2随机初始化种群中粒子的初始位置，选取聚类中心的初始点。

步骤3在约束条件下求出粒子的适应度值，并分别记录个体最优解和全局最优解。

步骤4通过公式（4）的K-均值算法划分子种群，获得新聚类中心，并用来更新相邻子种群的粒子位置。

步骤5比较新种群中粒子的适应度值，获得个体最优解，通过环拓扑循环得到粒子的局部最优解。

步骤6利用公式（5）更新粒子的位置。

步骤7判断是否满足终止条件，即是否已经达到设置的最大迭代次数，若满足，执行步骤8，若不满足，则返回执行步骤3。

步骤8终止优化运算，输出粒子最优位置。

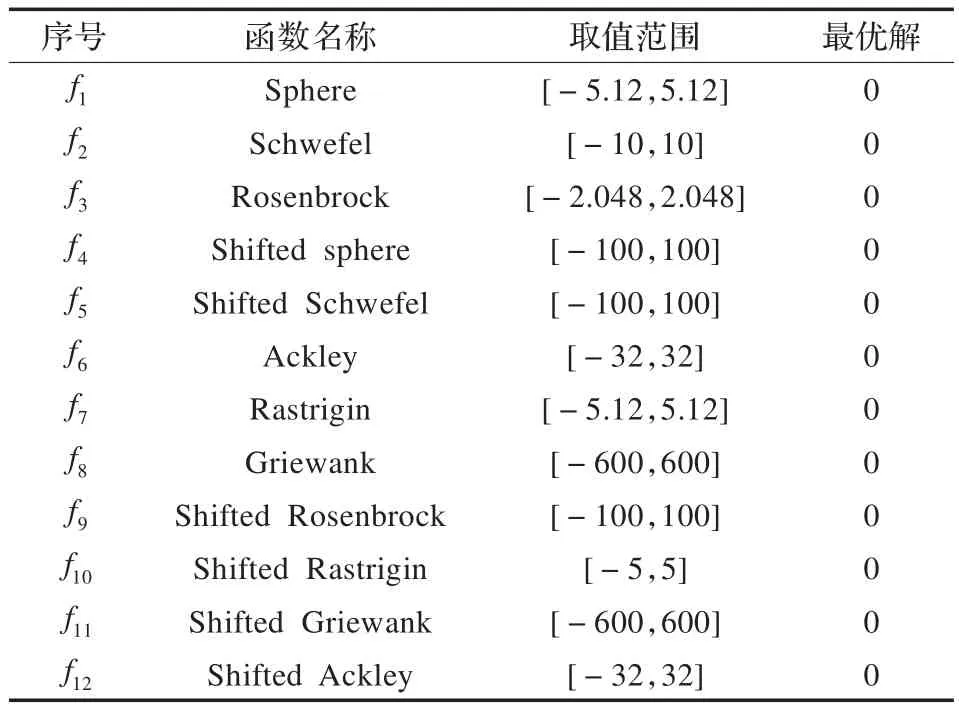
表1 12个测试函数说明

4.3 算法伪代码

KMS-CCPSO算法伪代码如下所示。其中，f表示划分的簇的个数；s表示每个子空间的维数；K表示子种群的数目；cidk表示第k个簇的聚类中心；Pjxi表示第j个子种群的第i个粒子的位置；Pj.yˆ表示第j个子种群的全局最优解；Pj.yˆ′i表示第j个子种群的第i个粒子的局部最优解。

5 仿真实验与结果分析

5.1 测试函数

为了测试本文提出算法的性能，采用了12个测试函数。其中，f1-f5函数是单峰函数，f6-f12函数是多峰函数，函数的具体取值范围和最优解如表1所示。

5.2 实验与结果分析

将本文提出的KMS-CCPSO算法与两个普通粒子群优化算法：PSO算法[4]和MSM-PSO算法[6]及处理高维问题的算法：CPSO-HK算法[11]和CCPSO2算法[14]进行比较。本实验采用MATLAB7.8进行仿真，系统软硬件环境为：2.20 GHz，4.00 GB内存，Windows7操作系统。实验中最大迭代次数为1 000次，粒子数目为36个，测试函数为100维，取30次运行结果的平均值。具体实验结果如表2所示。其中均值表示算法的寻优能力，方差表示算法的稳定性。

KMS-CCPSO算法的运行时间随着问题维数的增加会逐渐增加，仍与CCPSO2算法[14]的运行时间相当，优化性能却明显高于CCPSO2算法[14]。时间复杂度可表示为O(N×D×maxiter)，其中，N为粒子群数目，D为粒子维数，maxiter表示粒子群优化的最大迭代次数。

由表2可知，在均值指标中，除了f8测试函数外，KMS-CCPSO算法的收敛精度都高于其他对比算法，尤其是在f4测试函数中，收敛精度和稳定性明显高于其他算法；在方差指标中，本文算法稳定性明显高于对比算法。图2~7给出了KMS-CCPSO算法与其他四个对比算法在不同函数中的迭代进化曲线对比。从图中可以看出，从迭代初期开始，本文提出的KMS-CCPSO算法在收敛速度上就具有明显优势，且随着迭代次数的增加算法搜索到的解的精度也较高。图8~10给出了KMS-CCPSO算法与其他四个对比算法在不同维数下的最优解值。从图中可以看出，对比算法在不同的测试函数中，找到最优解的能力不同，如CPSO-HK算法[11]在f1和f2测试函数里随着位数的增加，其寻优能力依然较好，但是在f3测试函数里该算法的寻优能力逐渐变差。从图8-10中可以看出。KMS-CCPSO算法在不同的测试函数里随着维数的增加，其寻优能力保持平稳不变。由于篇幅有限，本文只列举了最具有代表性的6个测试函数在100维上的对比图及3个测试函数的维数递增曲线对比图，在其他的测试函数中，KMS-CCPSO算法上也具有相似的性能。

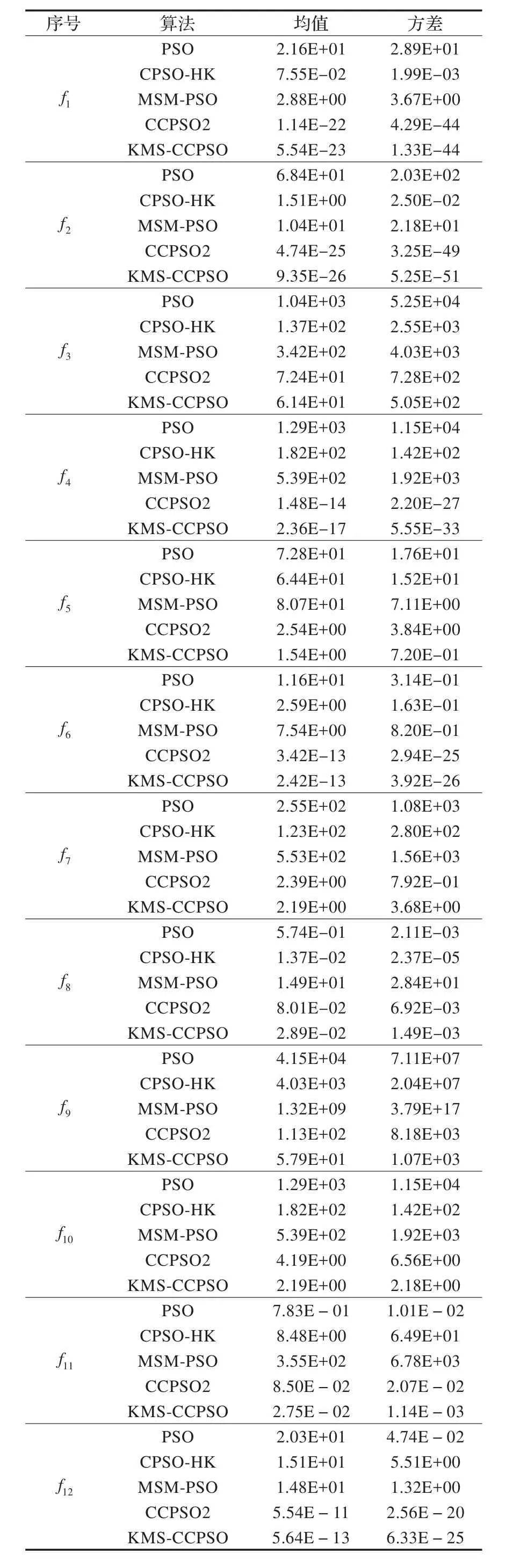
表2 五个算法的最优解平均值和方差比较

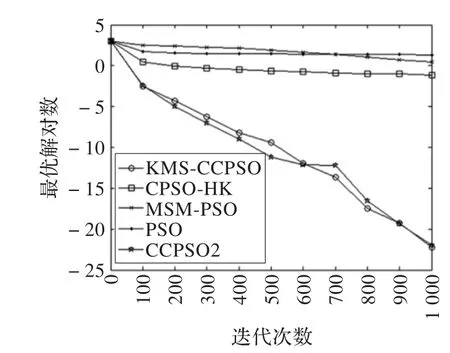
图2 f1迭代进化曲线对比图

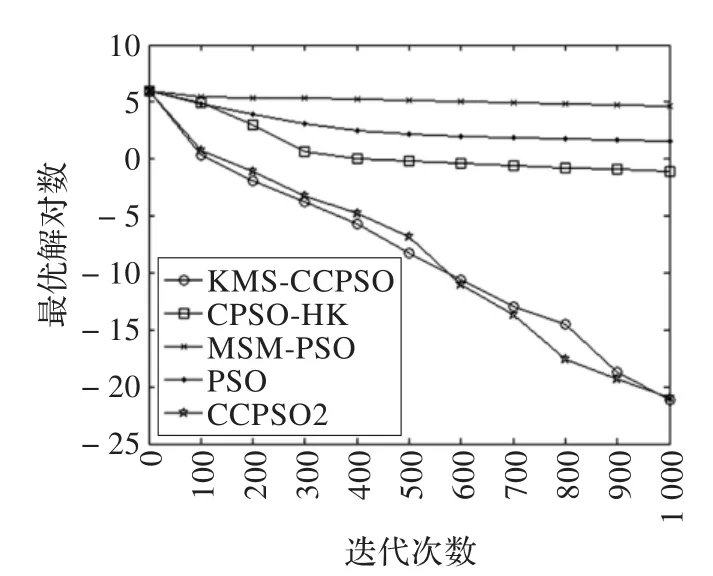
图3 f4迭代进化曲线对比图

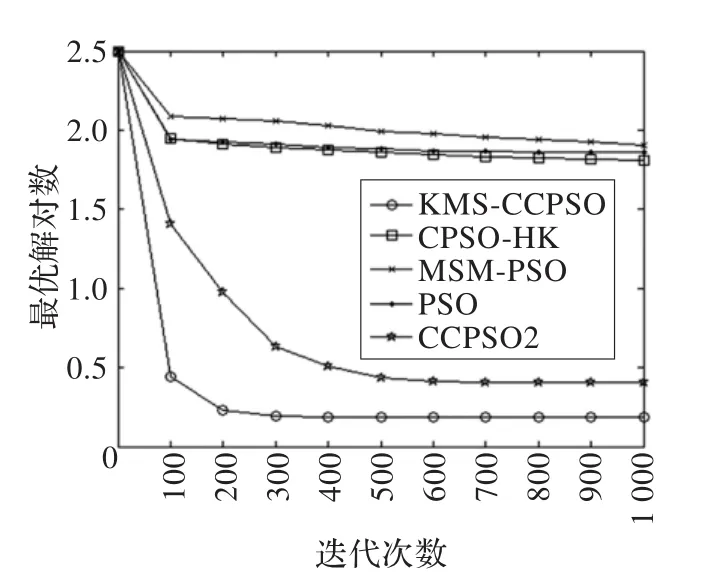
图4 f5迭代进化曲线对比图

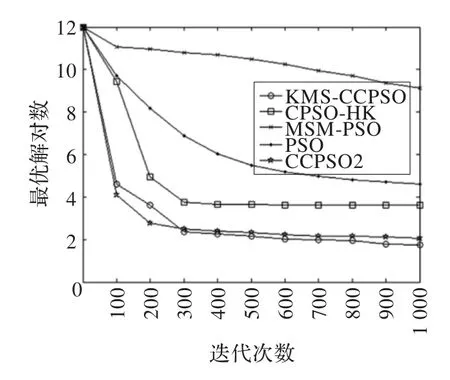
图5 f6迭代进化曲线对比图

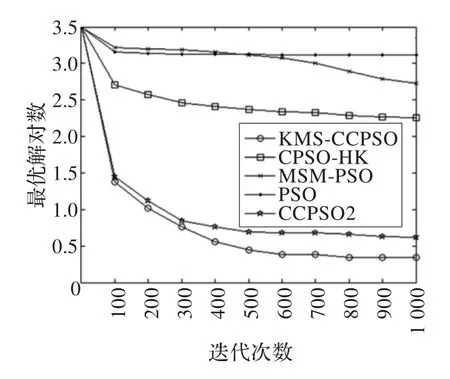
图6 f7迭代进化曲线对比图

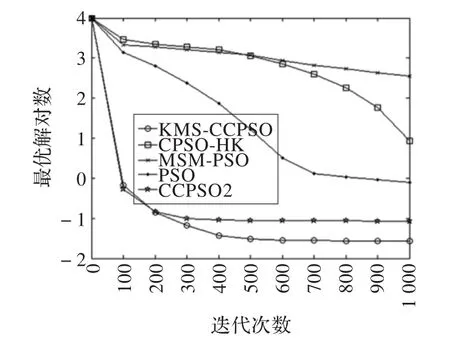
图7 f8迭代进化曲线对比图

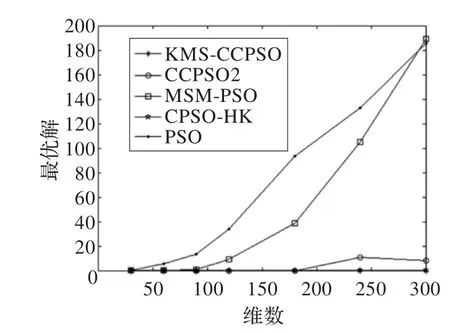
图8 f1维数增加的最优解对比图

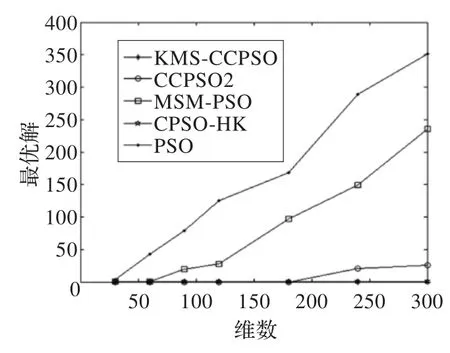
图9 f2维数增加的最优解对比图

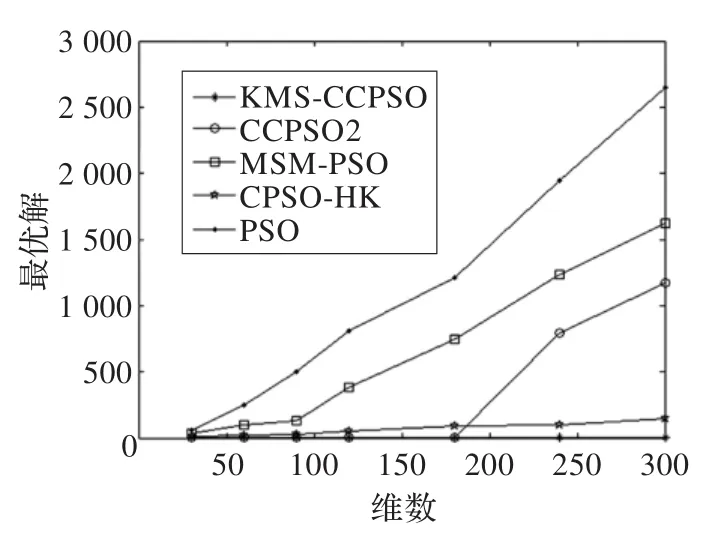
图10 f7维数增加的最优解对比图

6 结束语

针对现有的粒子群优化算法易陷入局部最优和处理高维优化问题性能差的问题，本文提出了基于K-均值的协同进化粒子群优化（KMS-CCPSO）算法，引入了分组策略、K-均值算法和高斯-柯西分布的位置更新公式，增加种群的多样性，有助于种群跳出局部最优。通过对12个测试函数的仿真实验验证了KMS-CCPSO算法具有较好的收敛精度和稳定性，能够较好地处理高维优化问题。

[1]Kennedy J，Eberhartr C.Particle swarm optimization[C]//Proc ofIEEE IntConfon NeuralNetworks.Perth：IEEE Piscataway，1995：1942-1948.

[2]Parsopoulos K E，Vrahatis M N.Recent approaches to global optimization problems through particle swarm optimization[J].Natural Computing，2002，1（2/3）：235-306.

[3]Poli R，Kennedy J，Blackwell T.Particle swarmoptimization an overview[J].Swarm Intelligence，2007，1（1）：33-57.

[4]Shi Y，Eberhart R.A modified particle swarm optimizer[C]//Proceedings of International Conference on Evolutionary Computation，Anchorage，Alaska，1998：69-73.

[5]Zhan Z H，Zhang J，Li Y，et al.Adaptive particle swarm optimization[J].IEEE Trans on Systems，Man，and Cybernetics-Part B：Cybernetics，2009，39（6）：1362-1381.

[6]徐冰纯，葛洪伟，王燕燕.基于多种群多模型协同进化的粒子群优化算法[J].计算机工程，2013，39（5）：200-208.

[7]Gies D，Rahmat-Samii Y.Particle swarm optimization for reconfigurable phase-differentiated array design[J].Microwave and Optical Technology Letters，2003，38（3）：168-175.

[8]Ursem R K，Vadstrup P.Parameter identification of induction motors using differential evolution[C]//The 2003 Congress on Evolutionary Computation，IEEE，2003，2：790-796.

[9]Foli K，Okabe T，Olhofer M，et al.Optimization of micro heat exchanger：CFD，analytical results and multiobjective evolutionary algorithms[J].Int J Heat Mass Transfer，2006，49（5/6）：1090-1099.

[10]Potter M A，De Jong K A.A cooperative coevolutionary approach to function optimization[C]//Proceedings of the Third Internation Conference on Parallel Problem Solving from Nature，Jerusalem，Israel，1994：249-257.

[11]Bergh F V D，Engelbrecht A P.A cooperative approach to particle swarm optimization[J].IEEE Trans on Evolutionary Computation，2004，8（3）：225-239.

[12]Yang Z Y，Tang K，Yao X.Large scale evolutionary optimization using cooperative co-evolution[J].Information Sciences，2008，178（15）：2985-2999.

[13]Omidvar M N，Li X，Yang Z，et al.Cooperative co-evolution for large scale optimization through more frequent random grouping[C]//2010 IEEE Congress on Evolutionary Computation（CEC），IEEE，2010：1-8.

[14]LI X D，YAO X.Cooperatively coevolving particle swarms for large scale optimization[J].IEEE Trans on Evolutionary Computation，2012，16（2）：210-224.

[15]Krishna K，Murty M N.Genetic K-means algorithm[J].Systems，Man and Cybernetics，1999，29（3）：433-439.