基于Dirichlet-to-Neumann 映射计算二维蜂巢状光子晶体的带隙结构

李 静， 胡 真

(河海大学 理学院，江苏 南京211100)

光子晶体［1］是一种新型的周期性人造材料，它的一个主要特征是具有光子带隙，频率落在带隙中的光不能够在光子晶体中传播。光子晶体的这个特征已被用于设计制造各种光子晶体器件，例如波导管弯曲［2-3］、分支［4］、频率滤波器［5］等。

在实际应用中，需要具有尽可能宽的带隙光子晶体结构。二维光子晶体由某种材料按照一定周期形式排列构成，如有正方形排列、三角形排列和蜂巢状排列等。其中蜂巢状排列的光子晶体由于能够用以设计出比较宽的完全带隙结构［6-7］，即光子带隙在两种偏振模式下存在重叠，因此在理论和工业上都被广泛研究［8-9］。在分析和设计蜂巢状排列的光子晶体的带隙结构中，有效的数值方法是必要的，而对带隙结构的分析可以转化为求解特征值问题。在标准的模型中［1］，特征值为ω2(ω 是角频率)，Bloch 波矢是给定的参数。对于一个非色散介质，这是一个线性特征值问题可以通过平面波展开法［10］、有限元法［11-12］、有限差分法［13-14］等进行求解;对于色散介质，这是一个非线性特征值问题。当介质是非色散的，可以利用柱面波展开法［15-16］等将问题转化成非线性特征值问题;另外基于传输矩阵法［17］、散射矩阵法［18］等建立起特征值问题，特征值为Bloch 波矢的一个函数，频率为给定的参数，这时即使介质色散，得到的也是一个线性特征值问题。

Yuan 等［19-20］提出利用DtN 映射计算正方形排列和三角形排列的二维光子晶体的带隙结构，通过建立合适的单元晶格DtN 映射，将带隙结构问题转化成特征值问题求解，特征值为Bloch 波矢的一个函数，频率ω 为给定的参数。DtN 映射实质是把单元晶格边界上的波动场映射成波动场的法向导数，利用DtN 映射避免了在单元晶格内部的离散，从而得到的是较小矩阵的特征值问题。

文中将利用DtN 映射计算蜂巢状排列的光子晶体的带隙结构，蜂巢状光子晶体的单元晶格由3 个正六边形组成。首先构造出这个特殊单元晶格的DtN 映射，然后将蜂巢状光子晶体的带隙结构问题转化成特征值问题求解。特征值问题中的矩阵是比较小的，如果在单元晶格每条边上离散N 个点，则矩阵的大小为(24N)× (24N)。

1 单元晶格上的DtN 映射

考虑标准的二维蜂巢状排列的光子晶体结构，如图1(a)所示。其中，白色圆柱代表空气洞，背景介质为硅板。对于一个折射率函数为n = n(x，y)的z方向上不变的二维结构，波沿xy 平面传播的情况下，控制方程是Helmholtz 方程:

其中，k0为自由空间波数;n 为折射率函数。在E 偏振模式下，u 是电场的z 分量并且μ = 1;在H 偏振模式下，u 是磁场的z 分量并且μ = n2。

图1 蜂巢结构光子晶体及其单元晶格Fig.1 Two-dimensional honeycomb photonic crystals and the unit lattice

文中方法是基于单元晶格上的DtN 映射，DtN映射是指把单元晶格边界上的波动场映射成波动场的法向导数，蜂巢状光子晶体的单元晶格Ω 由3个正六边形Ω1，Ω2，Ω3组成，如图1(b)所示。用Γ表示单元晶格Ω 的边界AB…L(图1(b)中的外围)。DtN 映射满足

其中，u 在Ω 中满足Helmholtz 方程;v 为边界Γ 的单位法向矢量。如果用uj1 ≤j ≤12 表示Γ 的12 条边AB，BC，…，KL，式(2)可以写成

如果在单元晶格Ω 每条边离散N 个点，那么DtN 映射Λ 可以用(12N)× (12N)的矩阵近似。单元晶格Ω 由3 个正六边形Ω1，Ω2，Ω3组成，为了计算单元晶格Ω 的DtN 映射Λ，首先需要计算3 个正六边形Ω1，Ω2，Ω3的DtN 映射Λ(j)(j =1，2，3)。这3 个正六边形的DtN 映射的构造过程和文献［19-21］相同。若Ω1，Ω2和Ω3的边界分别为Γ1(ABCDOL)，Γ2(KLOHIJ)和Γ3(ODEFGH)，那么Ω1，Ω2，Ω3的DtN 映射Λ(1)，Λ(2)和Λ(3)满足

为了构造Λ(j)(j = 1，2，3)的近似矩阵，首先写出Helmholtz 方程式(1)的通解，用极坐标(r，θ)表示:

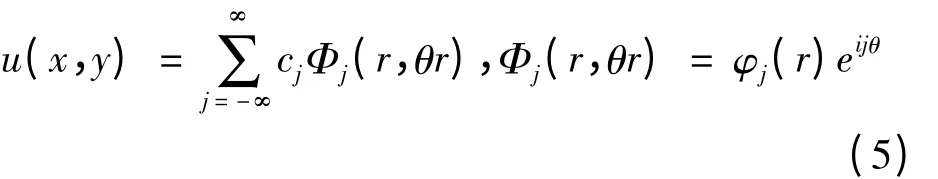
式中

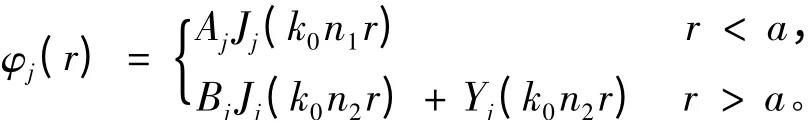
其中，n1为圆柱内部材料的折射率;n2为背景材料的折射率;系数Aj，Bj可以利用圆柱边界上的连续性条件求出。如果在边界Γj(j =1，2，3)的每条边上离散N 个点，通解式(5)可以近似写成

有了Λ(j)(j = 1，2，3)，就可以计算蜂巢状光子晶体单元晶格DtN 映射Λ。用u13，u14和u15表示边DO，LO 和HO，则DtN 映射式(4)可以写成:

将Λ(j)(j = 1，2，3)分成6 ×6 块，每一块是一个N ×N 的矩阵，表示为(1 ≤j ≤3，1 ≤s，t ≤6)，并且记

利用式(6)，可以写出单元晶格Q 边界上每一条边上的解的法向导数j = 1，…，12，则有

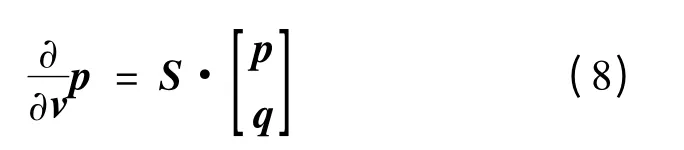
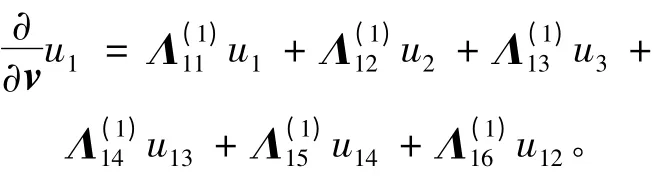
为了得到单元晶格Ω 的DtN 映射Λ，就要消除式(8)中的q，即u13，u14和u15，将S 分块成矩阵S11(12N ×12N)和S12(12N ×13N)，则有

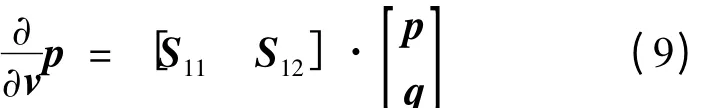
其中，q = ［u13，u14，u15］T可以通过式(6)建立方程组消除。如对于u13，由于u13为DO 边上的解，DO 边同时属于正六边形Ω1和六边形Ω3，利用Λ(1)和Λ(3)分别写出∂vu13的表达式，则有

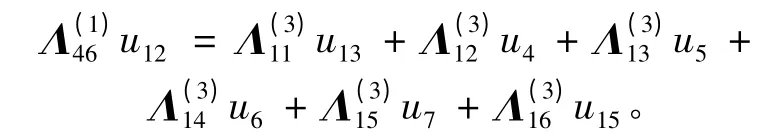
同样，关于u14和u15可以得到另外两个方程，从而得到方程组:

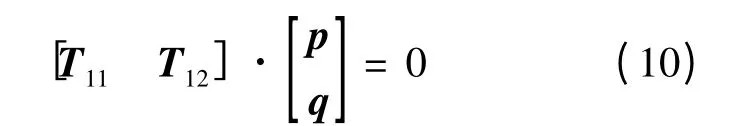
因此蜂巢状光子晶体的单元晶格Ω 的DtN 映射Λ 为

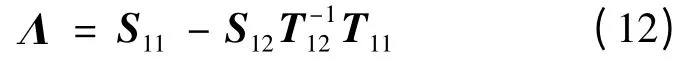
其中，Λ 为(12N)× (12N)的矩阵。

2 特征值问题

为了分析二维蜂巢状光子晶体的带隙结构，考虑方程式(1)的Bloch 模式解:

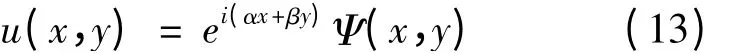
其中，(α，β)为Bloch 波矢;Ψ 为周期函数，与折射率函数n 遵循同样的周期。接下来利用DtN 映射Λ建立特征值问题。这里特征值问题的建立过程和文献［19-20］类似。由二维蜂巢状光子晶体结构的周期性，利用Bloch 模式解式(13)得到

其中ρα= eiαL/2，。如果把Λ 分块成12 ×12 的矩阵，每一块矩阵为N ×N 的，则可以得到如下方程:

将式(14)～式(16)带入式(17)，消除ui(7 ≤i ≤12)，∂vuj(1 ≤j ≤12)，化简得到

其中，M1，1，M1，2，…，M1，6，…，M6，6与ρα和ρβ相关。

蜂巢状排列的介质柱的布里渊区如图2 所示。

对蜂巢状排列的光子晶体，只需要寻找不可约布里渊区域边界上的Bloch 模式解。图2 中不可约布里渊区域是三角形阴影部分ΓMK，其中Γ(α = 0，β =0)，M(α = 0，β = 2π/)，K(α = 2π/3L，β =2π/)。从Γ 到M 有ρα= 1，ρβ为特征值;从M 到K 有ρβ= －1，ρα为特征值。对于K 到Γ 的情况，由于光子晶体的对称性，通过旋转K 到K'(α =4π/4L，β = 0)计算K 到Γ 的情况，此时ρβ= 1，ρα为特征值。

图2 蜂巢状排列的介质柱的布里渊区Fig.2 Brillouin zone of a honeycomb lattice of dielectric columns

最后无论在三角形区域ΓMK 的哪一条边上求解特征值，都可以写成

其中，U = (u1，u2，…，u6)T，特 征 值λ 和 矩 阵M0，…，M4定义如下:

1)从Γ 到M，λ = ρβ，0 ＜β ≤2π/，并且

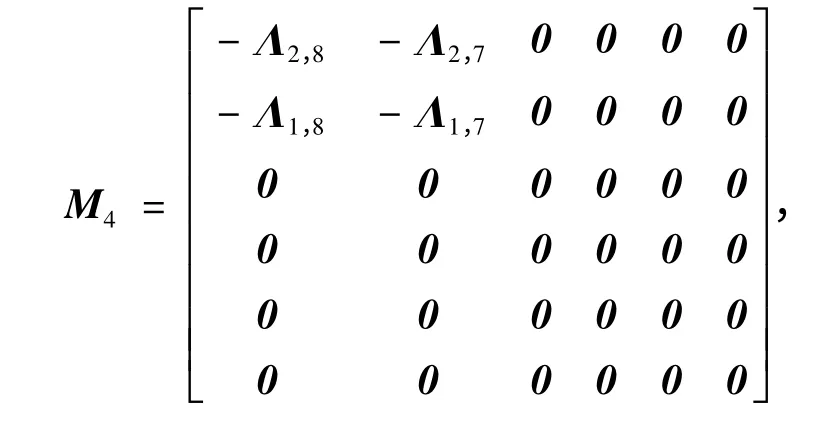
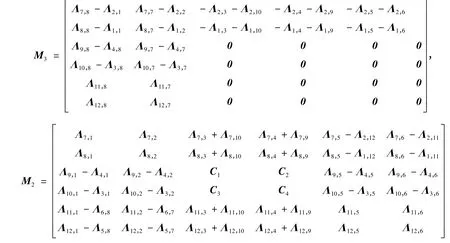
其中 C1= Λ9，3－ Λ4，3－ Λ4，10+ Λ9，10，

C2= Λ9，4－ Λ4，4－ Λ4，9+ Λ9，9，

C3= Λ10，3－ Λ3，3－ Λ3，10+ Λ10，10，

C4= Λ10，4－ Λ3，4－ Λ3，9+ Λ10，9。

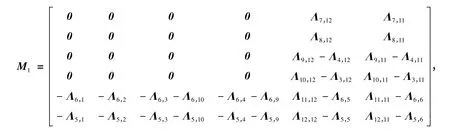
2)从M 到K，λ = ρα(0 ＜α ≤2π/3L)，并且M4，M3，M2，M1和M0同样是由DtN 映射Λ 的分块矩阵拼出来的大矩阵。

3)从K'到Γ，λ = ρα(0 ＜α ≤4π/3L)，且矩阵M0，M2，M4和情况2 的矩阵M0，M2，M4相同，矩阵M1，M3和情况2 的矩阵M1，M3符号相反。

将式(19)式改写为下面的线性特征值问题:

其中，I 为单位矩阵;V = ［λ3UT，λ2UT，λ1UT，UT］T。对于单元晶格Ω 每个边离散N 个点，矩阵Mj(0 ≤j ≤4)都是(6N)× (6N)的矩阵。因此线性特征值问题式(20)的矩阵是(24N)× (24N)的。

3 数值算例

通过计算两种不同的二维蜂巢状排列的光子晶体的带隙结构，验证文中建立算法的有效性。

首先考虑标准的二维蜂巢状光子晶体的带隙结构(见图1(a))。在此结构中，背景硅板上空气洞的大小一致，半径为a = 0.25L，L 是晶格常数。文中分别计算两种偏振模式下的带隙结构。首先是H 偏振模式(u 表示磁场的z 分量)的情况，控制方程为式(1)，其中μ = n2。背景介质硅板的有效折射率为n2= 2.91。此时由于标准情况下空气洞的大小相同，所以正六边形Ω2和Ω3完全一样，因此它们的DtN 映射也是一样的，即Λ(3)= Λ(2)。在单元晶格Ω每条边离散7 个点(N = 7)的情况下，特征值(20)的矩阵是(24N)× (24N)的。计算结果如图3(a)所示。其中，纵坐标是标准化频率ωL/(2πc)，ω 为角频率，c 为真空光速;横坐标为不可约布里渊区域的边界。虚线部分是光子带隙，频率范围为［0.523 3，0.544 8］。

然后计算E 偏振模式(u 表示电场的z 分量)的带隙结构，控制方程为式(1)，其中μ = 1。背景介质硅板的有效折射率为n2= 2.52，单元晶格Ω 每条边同样离散7 个点。计算结果如图3(b)所示。

图3 两种偏振模式下的光子能带结构Fig.3 Band structure of two-dimensional honeycomb photonic crystals is shown in Fig.1.1(a)

图3 (b)中，虚线部分为光子带隙，频率范围为［0.282 4，0.315 5］和［0.500 4，0.541 0］。蜂巢状光子晶体在E 偏振模式和H 偏振模式下的光子带隙有重叠(频率范围为［0.523 3，0.541 0］)，因此蜂巢状光子晶体在频率范围［0.523 3，0.541 0］里存在完全带隙。文中计算结果和文献［7］的结果是吻合的。

再考虑不标准的二维蜂巢状光子晶体的带隙结构，这时光子晶体中空气洞的大小是不一样的，如图4 所示，其中较大的空气洞的半径为r1=0.38L，较小的空气洞的半径为r2= 0.14L。此时构成单元晶格Ω 的3 个正六边形中，Ω2为包含较小空气洞的正六边形，Ω3为包含较大空气洞的正六边形，它们的DtN 映射Λ(2)与Λ(3)并不相同，需要分别计算。在单元晶格Ω 每条边上同样离散7 个点，计算结果如图5 所示。图5(a)为H 偏振模式下的带隙结构，有效折射率n2= 2.91，光子带隙的频率范围为［0.311 8，0.419 2］;图5(b)为E 偏振模式下的带隙结构，有效折射率n2= 0.52，光子带隙在频率范围［0.311 6，0.344 5］内。因此蜂巢状光子晶体在频率范围［0.311 8，0.344 5］里存在完全带隙。文中计算结果和文献［7］的结果完全一致的。

图4 不标准的二维蜂巢状光子晶体的带隙结构Fig.4 Two-dimensional honeycomb photonic crystals composed of two kinds of air holes

图5 两种偏正模式下的光子能带结构Fig.5 Band structure of two-dimensional honeycomb photonic crystals is shown in Fig.4

4 结 语

主要介绍利用DtN 映射建立起特征值问题计算二维蜂巢状排列的光子晶体的带隙结构。由于DtN映射避免了在光子晶体的单元晶格内部的离散，所以得到的是较小矩阵的特征值问题，可以快速求解，因此这种方法有利于分析和设计具有更好的带隙结构的蜂巢状光子晶体。

［1］Joannopoulos J D，Meade R D，Winn J N.Photonic Crystals:Molding the Flow of Light［M］.Princeton，NJ:Princeton University Press，1995.

［2］Smajic J，Hafner C，Erni D.Design and optimization of an achromatic photonic crystal bend［J］.Optics Express，2003，11(12):1378-1384.

［3］Ikuno H，Naka Y.Finite-difference time domain method applied to photonic crystals［J］.Electromagnetic Theory and Applications for Photonic Crystals，2006(103):401-443.

［4］Koshiba M，Tsuji Y，Hikari M.Time-domain beam propagation method and its application to photonic crystal circuits［J］.Journal of Lightwave Technology，2000，18(1):102.

［5］Ogusu K，Takayama K. Transmission characteristics of photonic crystal waveguides with stubs and their application to optical filters［J］.Optics letters，2007，32(15):2185-2187.

［6］Kalra Y，Sinha R K.Modelling and design of complete photonic band gaps in two-dimensional photonic crystals［J］. Pramana，2008，70(1):153-161.

［7］WEN F，David S，Checoury X，et al.Two-dimensional photonic crystals with large complete photonic band gaps in both TE and TM polarizations［J］.Optics Express，2008，16(16):12278-12289.

［8］Sondergaard T，Broeng J，Bjarklev A，et al. Suppression of spontaneous emission for a two-dimensional honeycomb photonic bandgap structure estimated using a new effective-index model［J］.Quantum Electronics，1998，34(12):2308-2313.

［9］YE J Y，Mizeikis V，XU Y，et al.Fabrication and optical characteristics of silicon-based two-dimensional photonic crystals with honeycomb lattice［J］.Optics Communications，2002，211(1):205-213.

［10］Johnson S，Joannopoulos J. Block-iterative frequency-domain methods for Maxwell＇s equations in a planewave basis［J］. Optics Express，2001，8(3):173-190.

［11］Axmann W，Kuchment P.An efficient finite element method for computing spectra of photonic and acoustic band-gap materials:I.scalar case［J］.Journal of Computational Physics，1999，150(2):468-481.

［12］Dobson D C.An efficient method for band structure calculations in 2D photonic crystals［J］.Journal of Computational Physics，1999，149(2):363-376.

［13］GUO S，WU F，Albin S，et al.Photonic band gap analysis using finite-difference frequency-domain method［J］.Optics Express，2004，12(8):1741-1746.

［14］YU C P，CHANG H C.Applications of the finite difference mode solution method to photonic crystal structures［J］.Optical and Quantum Electronics，2004，36(1):145-163.

［15］Nicorovici N A，McPhedran R C，Botten L C.Photonic band gaps for arrays of perfectly conducting cylinders［J］.Physical Review E，1995，52(1):1135.

［16］Ohtaka K，Ueta T，Amemiya K.Calculation of photonic bands using vector cylindrical waves and reflectivity of light for an array of dielectric rods［J］.Physical Review B，1998，57(4):2550.

［17］Pendry J B.Calculating photonic band structure［J］.Journal of Physics:Condensed Matter，1996，8(9):1085-1108.

［18］Botten L C，Nicorovici N A，McPhedran R C，et al. Photonic band structure calculations using scattering matrices［J］. Physical Review E，2001，64(4):046603.

［19］YUAN J，LU Y Y.Photonic bandgap calculations with Dirichlet-to-Neumann maps［J］.JOSA A，2006，23(12):3217-3222.

［20］YUAN J，LU Y Y. Computing photonic band structures by Dirichlet-to-Neumann maps:the triangular lattice［J］. Optics Communications，2007，273(1):114-120.

［21］HUANG Y，LU Y Y. Scattering from periodic arrays of cylinders by Dirichlet-to-Neumann maps［J］. Journal of Lightwave Technology，2006，24(9):3448.