磁浮球系统的二自由度控制

陈亚栋，张井岗，赵志诚

(太原科技大学电子信息工程学院，山西太原 030024)

磁浮球系统的二自由度控制

陈亚栋，张井岗*，赵志诚

(太原科技大学电子信息工程学院，山西太原 030024)

针对磁浮球系统提出了一种二自由度控制方法。它由反馈控制器、设定值前馈控制器和设定值跟随响应参考模型3部分组成。其中，采用基于期望干扰抑制性的直接综合法设计的反馈控制器用以保证系统的稳定和抑制干扰，前馈控制器和参考模型实现期望的设定值跟随响应。该控制器可以使设定值跟随特性和干扰抑制性解耦。仿真和实验结果表明:该方法可以使磁悬浮系统同时具有良好的设定值跟随性和干扰抑制性。

磁浮球系统;二自由度控制;直接综合法

近年来，磁悬浮技术作为一种高新技术以其独特的技术优势正在受到越来越多的关注。由于悬浮体与悬浮装置之间没有任何机械式接触，使得磁悬浮技术具有无摩擦、无噪音、无需润滑、功耗低、寿命长、维修成本低等优点，并且可以在液体、真空等特殊环境下工作，这使得它被广泛应用于磁悬浮列车、磁悬浮轴承、磁悬浮天平、磁悬浮隔震台、磁悬浮风洞以及人工磁悬浮心脏等方面［1］。

磁浮球系统是一个典型的非线性不稳定系统，是研究复杂的磁悬浮系统的基础平台。近年来国内外学者针对磁浮球系统提出了多种先进控制策略。W iboonjaroen W［2］根据磁浮球系统的线性化模型，利用状态观测器估计小球的位置，设计出状态反馈控制器。由于磁浮球系统是典型的非线性系统，电磁铁的电阻和电感会随着温度的变化而改变，因此模型失配时控制品质下降严重。文献［3-5］将模糊控制应用于解决磁悬浮系统的控制问题，该方法不需要精确的数学模型但是控制精度有待于提高。SUN ZG等［6］提出了滑模控制方法，虽然提高了系统的鲁棒性，但是抖震问题依然存在。Torres L H S等［7］利用反馈线性化得到系统的线性化模型，结合模糊控制器控制磁浮球系统，仿真研究表明控制策略的有效性。但这些控制方法都采用一自由度控制结构，不能同时得到良好的跟随性能和抗扰性能。而二自由度控制采用适当的设计方法，设计出两个独立的控制器，分别用于优化系统的设定值跟随特性和干扰抑制性。Ghosh A等［8］将二自由度控制推广到磁浮球系统，仿真研究表明该控制方法显著地提升了系统的跟随性能和抗扰性能，但其参数整定复杂，实际控制效果并不理想。

针对磁浮球系统，文中提出一种新型二自由度控制策略。利用基于期望干扰抑制性的直接综合法设计反馈控制器，保证系统的稳定性和良好的抗扰性;引入参考模型设计前馈控制器实现期望的设定值跟随响应。所设计的控制器结构简单，仅有两个可调参数，并分别与设定值跟随特性和干扰抑制性直接相关。仿真和实验结果表明，该二自由度控制可以使系统同时具有良好的位置跟随性能和抗干扰性能，进而证明了它的可行性。

1 磁浮球系统的数学模型

1.1 磁浮球系统的结构

文中研究的被控对象为Googol Technology公司的GML1001型磁浮球系统。该系统是一种典型的单自由度吸浮式磁悬浮系统，其结构简单，运行平稳，耦合度低，是进行先进控制策略研究的理想平台。它由被控钢球、光源、位置传感器、输入输出电路、驱动放大装置和控制器组成。磁悬浮系统结构如图1所示。

图1 磁悬浮系统结构框架Fig.1 Schem atic of themagnetic levitation system

1.2 磁浮球系统的数学模型

由于实际控制系统中存在多种外界干扰及多种耦合，很难建立精确的数学模型。在保证能够对系统实施精确控制的前提下，可以建立较为精确的数学模型。对此有必要进行如下假设:忽略电磁铁铁芯的漏磁以及磁场的边缘效应;磁感线呈均匀的线性分布，并且铁芯及气隙间的磁场强度以及磁通密度也是均匀分布的;铁芯和钢球的磁阻忽略不计;其他外界干扰因素忽略，钢球只受重力和电磁力，并且集中在几何中心。

通过对磁浮球系统受力分析，在竖直方向上小球的受力情况为

式中:m为小球的质量;x为钢球顶点到铁芯地面的位移;i为电磁铁的电流。

电磁铁产生的电磁力方程为

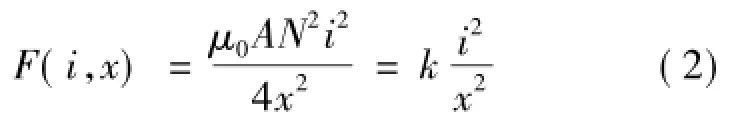
式中，k为电磁力常数。

根据电磁感应定律和基尔霍夫定律，电磁线圈的回路方程为

其中，R为线圈电阻;L为电磁铁线圈电感。在平衡点处有位置关系

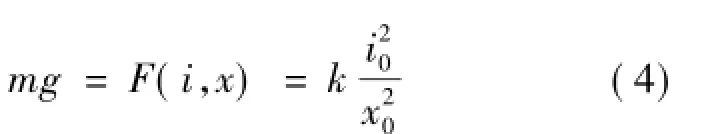
式中，i0，x0分别为平衡点处电磁铁的电流和小球位置。

通过以上方程分析可知，由于电磁力与电流i和位置x呈非线性关系，因此该系统为非线性系统。为了便于进行稳定性分析和控制器设计，将系统在平衡点处进行线性化处理。对式(2)按泰勒级数展开，舍掉高次项后进行拉普拉斯变换，并进行整理得到

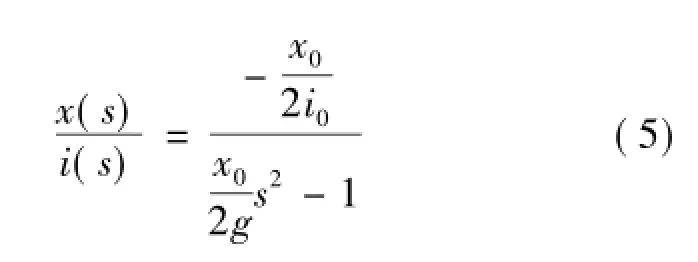
为了便于控制器设计，在控制器输出和传感器输出端建模，ks为小球位置到传感器量测电压的变换系数，ka为驱动放大器将控制电压转换为电流信号的变换系数。经化简，系统的数学模型可写为

其中M=－(ks/ka)(x0/i0)，T=x0/2g。

该实验装置的物理参数由表1给出。经计算，系统的数传递函数为

由系统的开环传递函数可知，系统存在位于s平面的右半平面的极点，因此是开环不稳定系统。

表1 物理参数Tab.1 Physical parameters

2 二自由度控制

文中提出的二自由度控制结构如图2所示。其中，r，y，d分别表示系统的设定值输入、系统输出和干扰输入;Gp(s)为被控对象磁浮球系统。所提出的二自由度控制结构包含3部分:GC(s)，GF(s)和GR(s)分别表示反馈控制器、前馈控制器和参考模型。其中，反馈控制器用于保证系统稳定和抑制干扰，前馈控制器和参考模型实现期望的设定值跟随响应［9］。

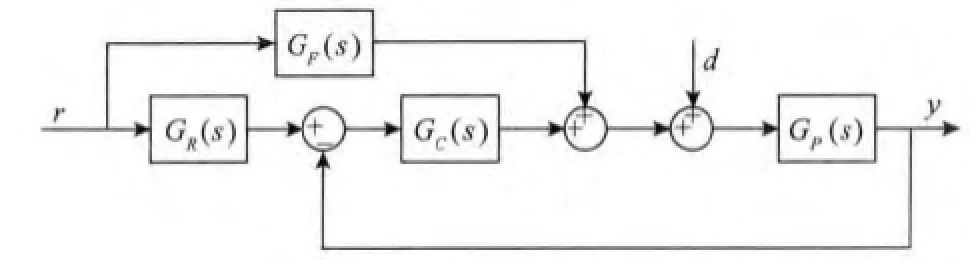
图2 二自由度控制结构Fig.2 Block diagram of the 2-DOF control

由图2可得系统的设定值跟随响应和干扰响应

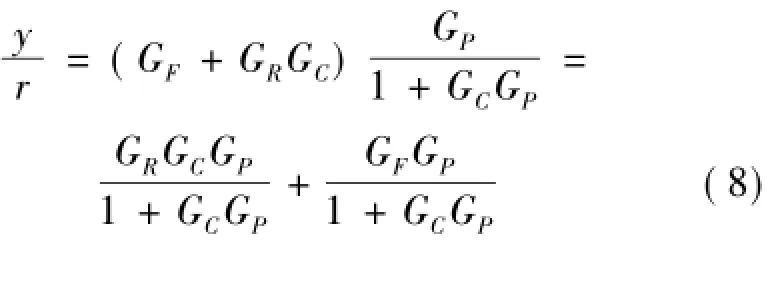
根据反馈控制系统的内稳定性，在GF(s)和GR(s)稳定的情况下，可以利用设计反馈控制器GC(s)保证系统是稳定的。

由式(8)可知，如果存在可实现的前馈控制器GF(s):

则系统的跟随特性变为

在这种情况下，系统的设定值跟随特性和干扰抑制性实现解耦。同时可以看出，在模型精确且没有干扰的情况下，系统处于开环状态，因此反馈控制的作用在于克服干扰以及模型不确定性对系统的影响。

为了获得较好的跟随特性，并考虑到GF(s)的可实现性，GR(s)选择为

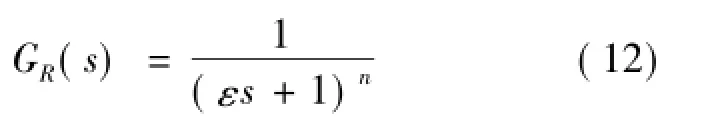
式中:ε为可调参数;阶次n为Gp(s)的相对阶次。

根据式(10)和式(12)，可以得到

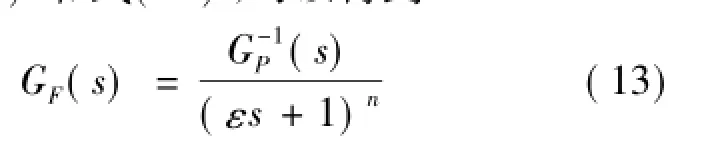
为了使系统获得良好的抗扰性能，利用基于期望干扰抑制性的直接综合法［10］设计反馈控制器GC(s)。

由式(9)可以得到

由式(14)可以给出期望的干扰抑制特性(y/d)d，同时设计反馈控制器Gc(s)。

反馈控制器采用经典的PID控制器形式

将式(14)和式(7)代入式(9)，得到系统的干扰响应

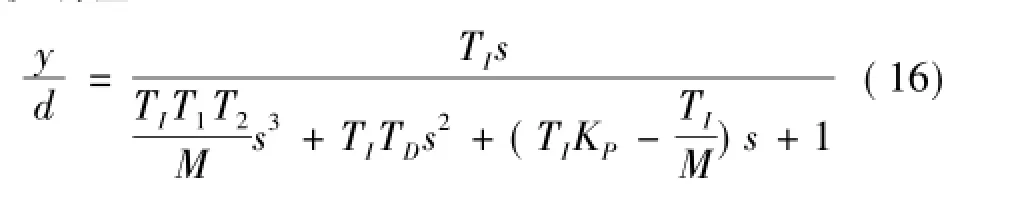
根据式(16)，为了得到良好的抗扰性能并考虑到Gc(s)的PID结构，将期望的干扰抑制性设为

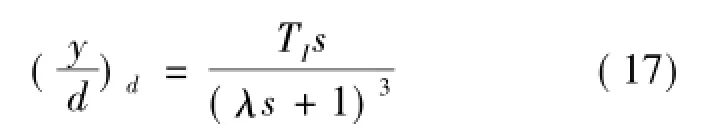
式中，λ为可调参数。

通过对比式(16)和式(17)的对应阶次的系数，可以得到反馈控制器的PID参数如下:

通过上述步骤设计的二自由度控制器结构简单，仅有两个可调参数ε和λ。由式(11)和式(12)可以看出，在模型精确的情况下，系统的设定值跟随特性是无超调的，并且仅与控制参数ε相关:通过整定较小的ε值可以获得较快的跟随响应，但是需要较大的控制器输出量。而整定较大的ε值可以使跟随响应变缓，同时需要的控制器输出量也减小。由式(15)和式(17)可知，λ决定了系统的干扰抑制特性，同时决定了系统的鲁棒性。减小λ可以获得更好的干扰抑制性，但是鲁棒性将变差;增大λ会使干扰抑制性变差，但是鲁棒性得到提升。因此，λ的选择要兼顾干扰抑制性和鲁棒性，具体参数可根据计算机辅助分析确定。

3 仿真与实验

为验证文中所提出的设计方法的有效性，使用Matlab软件进行仿真研究，并进行实时控制实验。

3.1 仿真

给定输入信号和扰动信号分别为

与文献［8］中提出的二自由度控制方法在相同的实验条件下进行对比研究。仿真结果分别如图3～图6所示。其中，图3～图5分别表示所设计的控制器在不同控制参数下的响应曲线，图6表示文献［8］中方法在相同实验条件下的响应曲线。

图3 ε=0.2，λ=0.02时位置跟踪曲线Fig.3 Position track ing curve(ε=0.2，λ=0.02)

图4 ε=0.01，λ=0.1时位置跟踪曲线Fig.4 Position tracking curve(ε=0.01，λ=0.1)

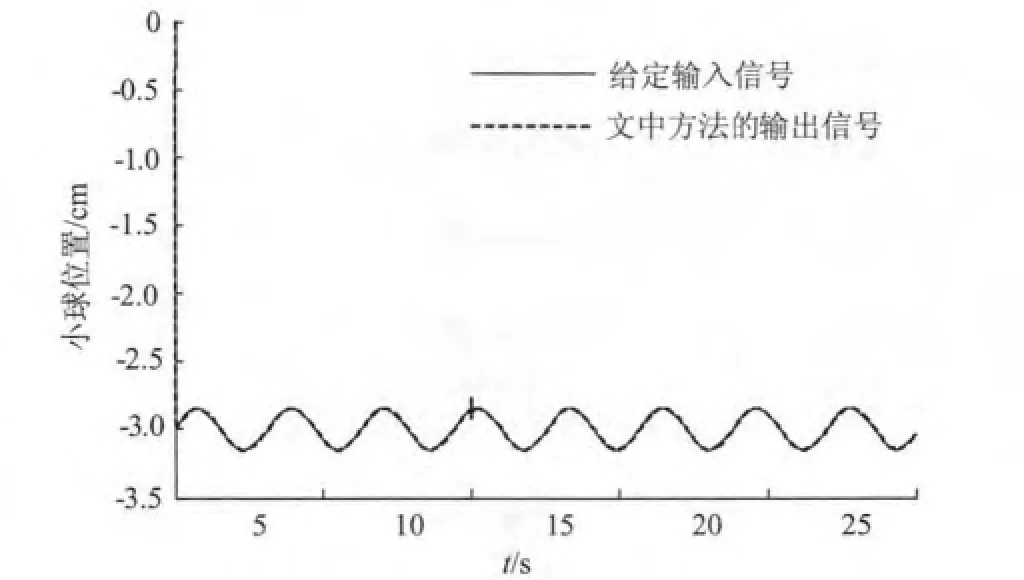
图5 ε=0.01，λ=0.02时位置跟踪曲线Fig.5 Position tracking curve(ε=0.01，λ=0.02)

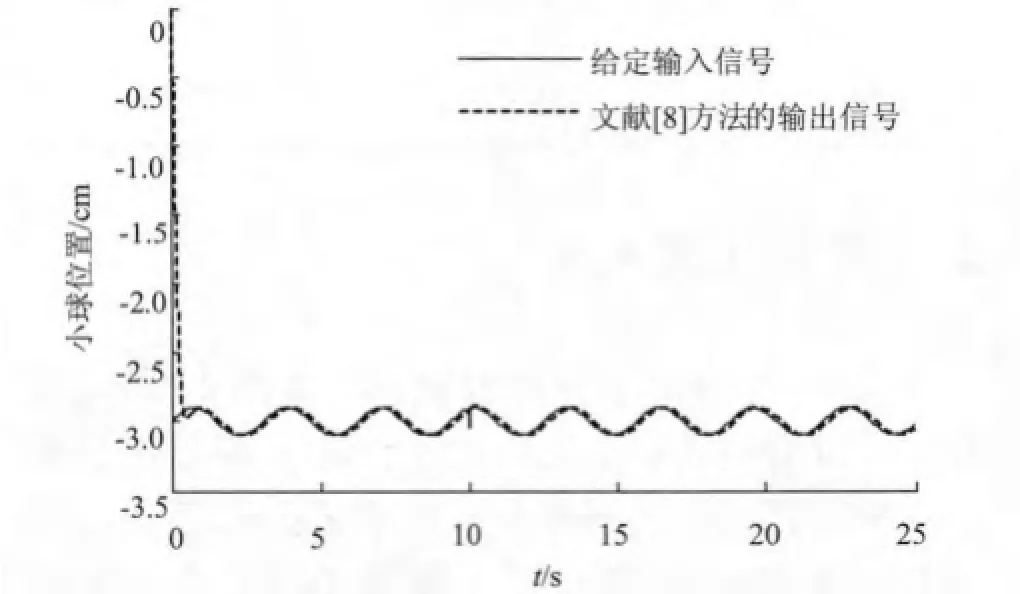
图6 α=20时位置跟踪曲线Fig.6 Position tracking curve(α=20)

由图3～图5可知，较小的ε的值可以得到较快的设定值跟随响应，相反较大的ε值可以使设定值跟随响应变缓，但抗扰性不受影响;类似地较小的λ值可以得到较好的干扰抑制性，而增大λ则干扰抑制性变差。考虑到实验装置的输出能力有限，因此ε值的选取不可能过小，而λ的选择要兼顾系统的鲁棒性和干扰抑制性，最终选取图5所示的参数值取得最好的控制效果。通过仿真结果可知，该二自由度控制可以使被控钢球在很短的时间内达到稳定状态，并有较好的动态特性。经反复实验，文献［8］中的方法在a=20时取得最好的控制效果，对比图5和图6可知，系统的设定值跟随特性和干扰抑制性均优于文献［8］中的方法。

3.2 实验

为了验证该方法的实际控制效果，文中还进行了实时控制实验。输入信号同样选为r(t)= 0.15sin(2t)－3，为了验证系统的抗扰性，在系统到达稳定状态后，在被控钢球下增加一个相同的钢球作为干扰信号，实验结果如图7、图8所示。

实验结果表明，文中提出的控制策略在实时控制时能使被控钢球迅速跟踪给定信号，并有很好的抗扰能力，设定值跟随特性和干扰抑制性均优于文献［8］中的控制策略。

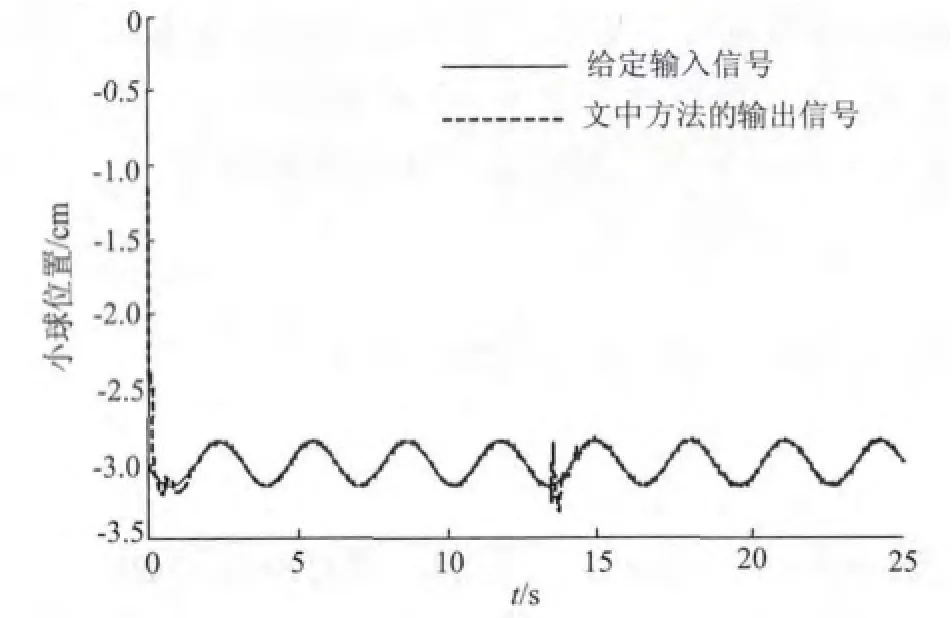
图7 ε=0.01，λ=0.02时实时控制输出曲线Fig.7 Real-time control output curve(ε=0.01，λ=0.02)

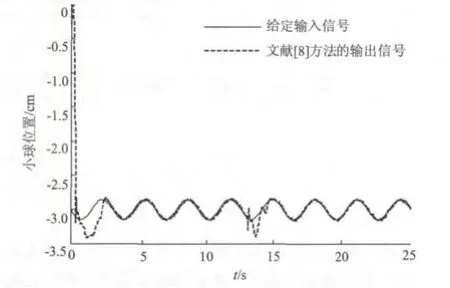
图8 a=20时实时控制输出曲线Fig.8 Real-tim e control outpu t cu rve(a=20)

4 结语

文中提出了磁浮球系统的一种二自由度控制策略。该方法结合参考模型设计前馈控制器提高了系统的设定值跟随特性，利用直接综合法设计反馈控制器保证系统具有良好的抗扰性能。所设计的控制器结构简单，仅有两个可调参数，并且实现了设定值跟随特性和干扰抑制性解耦。通过仿真和实验研究可知，该方法可以使磁浮球系统同时获得良好的设定值跟随特性和干扰抑制特性。

［1］Kumar E V，Jerome J.LQR based optimal tuning of PID controller for trajectory tracking of magnetic levitation system［J］.Procedia Engineering，2013，64:254-264.

［2］Wiboonjaroen W，Intachot T.Real time implementation of the state-PI feedback control scheme and state-observer for amagnetic levitation system［J］.Journal of the Japan Society for Simulation Technology，2011，24(8):635-644.

［3］Ahmad A K，Saad Z，Osman M K，et al.Control ofmagnetic levitation system using fuzzy logic control［C］//Second International Conference on Computational Intelligence，Modelling and Simulation(CIMSiM).Bali:IEEE，2010:51-56.

［4］Dragos C A，Preitl S，Precup R E，et al.Takagi-Sugeno fuzzy controller for a magnetic levitation system laboratory equipment［C］//International Joint Conference on Computational Cybernetics and Technical Informatics(ICCC-CONTI).Tim isoara:IEEE，2010:55-60.

［5］Yadav S，Tiwari JP，Nagar SK.Digital control ofmagnetic levitation system using fuzzy logic controller［J］.International Journal of Computer App lications，2012，41(21):22-26.

［6］SUN Z G，Cheung N C，ZHAO SW，et al.The application of disturbance observer-based sliding mode control for magnetic levitation systems［J］.Proceedings of the Institution ofMechanical Engineers，Part C:Journal ofMechanical Engineering Science，2010，224(8):1635-1644.

［7］Torres L H S，Vasconcelos Jr C A V，Schnitman L，etal.Exact linearization and fuzzy logic applied to the Control of amagnetic levitation system［C］//IEEE International Conference on Fuzzy Systems(FUZZ).Barcelona:IEEE，2010:1-5.

［8］Ghosh A，Krishnan T R，Tejaswy P，et al.Design and implementation of a 2-DOF PID compensation for magnetic levitation systems［J］.ISA Transactions，2014，53(4):1216-1222.

［9］LIU T，ZHANGW，GU D.Analytical design of two-degree-of-freedom control scheme for open-loop unstable processes with time delay［J］.Journal of Process Control，2005，15(5):559-572.

［10］CHEN D，Seborg D E.PI/PID controller design based on direct synthesis and disturbance rejection［J］.Industrial and Engineering Chemistry Research，2002，41(19):4807-4822.

(责任编辑:邢宝妹)

2-DOF Control Schem e for M agnetic Levitation Ball System

CHEN Yadong，ZHANG Jinggang*，ZHAO Zhicheng
(School of Electronics and Information Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China)

A novel two-degree-of-freedom(2-DOF)control scheme for amagnetic levitation ball system is proposed in this paper.It contains three parts:the feedback controller，the set-point feed forward controller and the referencemodel.The feedback controller based on the direct synthesis approach and desired disturbance rejection characteristics are used to guarantee the stability of the system and suppress the disturbance.The desired set-point tracking response is achieved by the feedforward controller and the referencemodel.The set-point tracking performance and the disturbance rejection characteristics of the system can be decoup led by the designed controller structure.Both simulation and experimental results show that the novel 2-DOF control scheme has a good set-point tracking performance and the disturbance rejection characteristics.

magnetic levitation ball system，2-DOF control，direct synthesis approach

TP 273

A

1671－7147(2015)06－0741－05

2015－07－27;

2015－09－29。

山西省回国留学人员科研项目(2013－092);山西省青年科技研究基金项目(2014011020－1);山西省研究生创新项目(2015SY65)。

陈亚栋(1989—)，男，河北涿州人，控制工程专业硕士研究生。

*通信作者:张井岗(1965—)，男，山西运城人，教授，硕士生导师。主要从事先进控制技术及应用研究。

Email:chenyad007@163.com