一种基于稳态增益的非线性控制器及其应用

刘宝，段慧，王君红，张文杰，康忠健

(中国石油大学(华东)信息与控制工程学院，山东东营 257061)

一种基于稳态增益的非线性控制器及其应用

刘宝，段慧，王君红，张文杰，康忠健

(中国石油大学(华东)信息与控制工程学院，山东东营 257061)

基于控制系统的稳态控制增益，提出一种新的非线性脉冲控制体系架构及其控制算法。该非线性脉冲控制算法(IMNC)包括动态控制单元、稳态控制单元和协同输出控制单元3部分。在协调控制单元作用下，动态控制单元利用快速脉冲输出控制，提高系统的上升时间，并使工艺变量快速接近稳态值;稳态控制单元依据控制器将来的稳态输出值，结合比例或积分控制作用，快速消除控制偏差，提高控制精度。最后分别选择大纯滞后和非最小相位作为控制对象，进行控制效果检验。仿真结果表明，IMNC的控制性能优于传统PID控制算法，对提高复杂对象控制效果具有一定的实际意义。

控制增益;非线性;脉冲控制

随着现代工业社会的发展，出现了越来越多的复杂控制对象，同时对产品质量的要求也越来越高，这导致传统的控制规律难以适应这种控制需求。为了提高控制效果，从上世纪70年代开始，人们从工艺操作经验或生物控制规律出发，研究发展出现了专家控制系统［1-3］、神经网络控制系统［4-6］和模糊控制系统［7-12］以及预测控制［13-14］等智能控制算法。这些控制算法为提高复杂控制对象控制效果起到了很大作用。但是这些控制算法或规律都比较复杂，实现难度较大，影响实际应用推广。

借鉴专家控制思想，文中根据实际优化工艺操作经验设计了一种非线性脉冲控制算法(IMNC)。IMNC包括动态控制算法和稳态控制算法及协调输出3部分。产生控制偏差时，在协调控制单元作用下，动态控制单元利用快速输出脉冲，提高系统的上升时间，并使工艺变量快速接近稳态值;然后，稳态控制单元依据控制器将来的稳态输出值，快速消除控制偏差，提高控制精度。IMNC的动态控制单元和稳态控制单元独立较强，使得很容易实现调节控制参数。通过仿真实验结果表明，IMNC具有较好的控制性能，并具有较好的实际应用意义。

1 受启发来源

在实际工艺操作过程中，对于有经验的操作者而言，他们总是能够以较快的速度、较小的超调量和较短的调节时间，使控制系统快速达到稳定状态。例如，在调节某容器液位过程中，如果液位低于目标值比较大，操作者一般先把进料阀位开到接近最大，待液位快要接近目标值时，再迅速减小阀位，从而使工艺变量能够以快速、无超调地达到稳定值。其调节规律如图1所示。另外，多数优化控制规律具有类似的脉冲输出调节规律。在理想状态下，这种调节规律能够使工艺变量以较快的上升时间、无或较小超调和较小的调节时间，快速达到稳定状态。文中提出的非线性脉冲控制算法，就是受这种调节规律启发而设计的。

图1 一般脉冲调节规律Fig.1 Normal rule of im pu lse ad justment

2 脉冲控制算法原理

2.1 脉冲控制体系架构

受图1所示的脉冲调节规律启发，设计一种非线性脉冲控制算法。该脉冲控制算法的体系结构如图2所示，包括动态控制单元、稳态控制单元和协调输出控制单元。

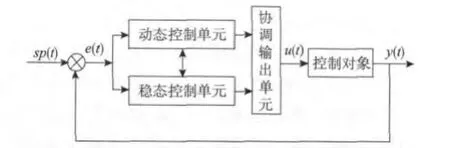
图2 脉冲控制系统体系架构Fig.2 System structu re of IM NC

其中动态控制单元主要承担动态变化过程的控制调节任务，利用快速脉冲输出控制，提高系统的上升时间，并使工艺变量快速接近稳态值;稳态控制单元主要承担消除稳态变化过程的控制误差，依据控制器将来的稳态输出值，结合比例或积分控制作用，快速消除控制偏差，提高控制精度;协调输出单元则是根据控制系统的运行状态，负责协调动态控制单元和稳态控制单元的工作状态，形成最终控制输出信号。

为了进一步描述脉冲控制算法，进行如下参数定义:(1)设控制器设定值改变之前，控制器的初始稳态输出值为u0(t);(2)uL和uH分别表示控制器的输出底限和高限值;(3)up(t)为设当控制系统设定值改变或受到干扰后，在动态变化调节解过程中，控制器的最大脉冲输出峰值;tp为控制器输出达到up(t)的时间;td为控制器输出达到up(t)之后开始反方向变化的时间;(4)uup(t)，udown(t)分别表示控制脉冲输出的上升和下降变化输出值;(5)us(t)表示控制器的稳态过程控制输出信号;(6)uss(t)为消除控制偏差之后控制器的稳定输出值。

2.2 动态控制单元算法

根据图1所示的调节规律，动态控制单元要使控制对象的动态变化过程具有较短的上升时间、较小的超调量。因此，设计其动态控制单元的输出变化过程，包括上升变化和下降变化两个阶段。

2.2.1 上升变化规律假设已知控制器的稳态输出uss(t)。在设定值发生变化或受到阶跃干扰时，控制器迅速输出到峰值up(t)。相对于控制器初始输出值u0(t)，其变化量Δup(t)为其中，α为正脉冲增益系数，且保证uL≤Δup(t)≤uss(t)或uss(t)≤Δup(t)≤uH。

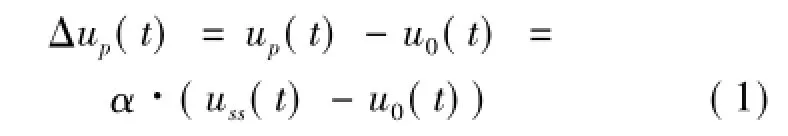
为了使控制器从u(t0)比较稳定地变化到u(tp)，设计一个滤波环节

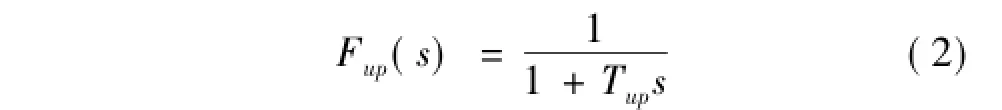
其中，TuP为脉冲上升滤波时间常数，且Tup≪tp。综合式(2)，(3)，且考虑拉斯变换形式，可以得到脉冲输出的上升变化规律:

其中，Uup(s)，U0(s)，Uss(s)分别为uup(t)，u0(t)，uss(t)的拉斯变换。由式(3)可知，uup(t)初始值为u0(t)，其稳定变化值为u0(t)+α·(uss(t)－u0(t))。

2.2.2 下降变化规律当控制时间大于td时，控制器的输出信号又迅速地变化到将来的稳态输出值uss(t)附近。同样为了使控制器较为稳定地变化到uss(t)且保证一定的调节效果，设计一个滤波环节

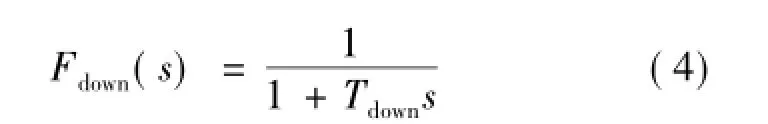
因此，脉冲下降变化规律为

由式(4)，(5)可知，udown(t)初始值为up(t)，其稳定变化值为uss(t)。

2.3 稳态控制单元算法

稳态控制单元的作用主要是，保证稳定消除控制偏差和提高控制精度。设控制器进入稳定控制单元控制算法的时间为ts，且令ts=td+βTdown，β≈3.0～4.0。为了进一步快速消除控制偏差，当t＞ts时，稳态控制算法在脉冲下降控制算法的基础上，增加适当比例作用，即

Us(s)=Udown(s)+Kp·E(s)(6)

其中，Kp为比例系数。如果uss(t)与实际理想uss相同，则稳定控制算法按照式(6)规律进行控制即可，并且当控制偏差为零时，us(t)=uss(t)。

当时间t大于β倍工艺时间常数T即，t＞βT时，如果因为系统非线性或控制器稳态输出与理想稳态输出存在偏差，则导致不能够完全消除控制偏差。此时，可采用增加适当积分作用，即当控制偏差ess(t)≈0时，us(t)≠uss(t)，此时要用控制器输出值us(t)更新稳态uss(t)。

如果uss(t)比较理想，只采用控制规律(6)即可。因为此时采用控制规律(7)必然会引起工艺系统振荡。实际上在大多数情况下，不能够准确计算出控制器稳态输出。这种情况下需要结合控制规律式(6)，(7)，即当ts≤t＜βT时，采用控制规律(6);当t≥βT时，采用控制规律(7)，且当控制偏差消除时，更新原计算uss(t)。

如果在设定值没有改变，也就是在稳定控制过程中，如果出现随机干扰时，因为此时设定值并不发生变化，因此此时的Uss(s)已知。如果控制偏差大于某一个阈值时，采用控制规律(6)，只是采用已经得到更新的uss(t)，设为u'ss(t)，即

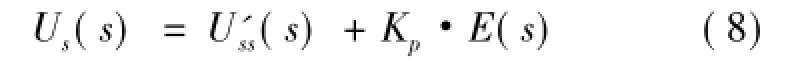
2.4 协调输出控制单元

当设定值发生变化时，当时间0≤t≤td时，控制器输出动态脉冲上升输出Gc(s)=Uup(s);当时间td＜t≤ts时，控制器输出动态脉冲下降输出Gc(s)=Udown(s)，即在0＜t≤ts时，动态控制单元处于工作状态。

当时间ts≤t＜βT时，控制器输出稳态控制算法采用式(6);当t≥βT时，采用控制规律(7)，且当控制偏差消除时，更新原计算uss(t)。当工艺系统达到稳定之后，如果出现随机干扰，则采用控制规律(8)，即当时间t＞ts时，稳定控制单元处于工作状态。

当设定值再次发生变化时，控制器时间清零t=0，重复进行述控制阶段。

2.5 辨识工艺模型参数

在该脉冲控制算法中，控制器在消除控制偏差后的稳定输出uss(t)非常关键。对于大多数化工过程而言，均可以在其工作点附近一定范围内，用式(9)来近似表示:

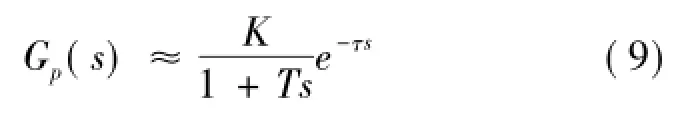
其中，K，T，τ分别为非线性过程的放大增益、大致时间常数和纯滞后时间。如果过程工艺对象的稳态输出值为Yss(s)。因为控制系统稳定时，根据终值定理，有式(10)成立:

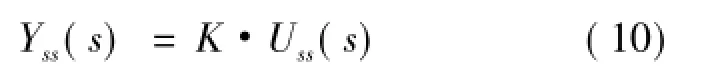
因为稳定时，工艺变量稳态值与工艺设定值相同，即Yss(s)=SP(s)，故有

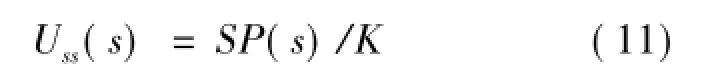
因此，只要获得工艺对象的稳态放大增益系数K，则很容易计算得到控制器的稳态输出uss(t)。对于大多数化工过程对象传递函数可以表示为式(9)所示的通用传递函数。由式(10)或式(11)可知

因此，稳态放大增益系数K可以很容易利用阶跃响应法或矩形脉冲响应法获得，同时也可以利用两点法得到工艺对象的大致时间常数为T和滞后时间为τ。

2.6 控制参数调整算法

该脉冲控制算法的动态控制单元和稳态控制单元两部分之间的独立性比较强，可以单独进行参数调整:

1)根据工艺系统的动态变化过程的上升速度和超调量大小，调整α或td。如果超调量过大或上升速度过快，可适当减少α值或td;反之，则适当增大。

2)根据稳态过程变化情况，调整比例系数和积分系数。如果趋向稳态状态速度较慢，可适当增加比例系数Kp;反之减小比例系数。如果控制精度较低，可适当增大积分作用系数。

2.7 稳定性分析

动态特性控制算法只影响动态响应部分。只有稳态控制算法才对控制系统的稳定性产生影响。实际上，因为当t＞βT时

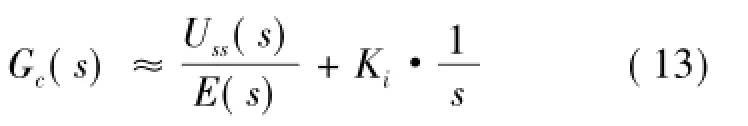
根据工艺对象模型(9)和式(13)，可以得到系统闭环传递函数为

进一步可以得到系统特征方程为

由式(15)可以看出，除常量Uss(s)和工艺过程有关的Gp(s)，E(s)外，只有积分作用参数Ki影响整个控制系统的稳定性，这使得整个控制系统实现稳定控制。

3 仿真实验

为了检验文中提出的非线性脉冲控制算法的控制性能，选取工艺对象(16)，(17)为控制对象。其中，对象(16)是一个一阶惯性大纯滞后工艺对象，且τ/T≫1，其传递函数为［15］

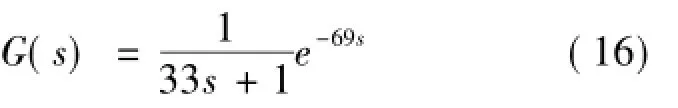
如果利用常规控制算法控制该对象，很难获得好的控制效果。对象(17)的传递函数为［13］

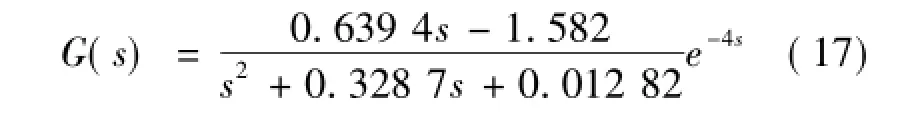
该模型非最小相位系统，且具有反向特性和纯滞后。非最小相位系统在控制工程中普遍存在，如船舶航向控制系统、鱼雷定深控制系统、水轮机控制系统等。设计非最小相位控制系统必须满足多方面的性能要求，这是一个控制难题。对传统PID均难以控制这两个控制对象。

对IMNC的控制性能和传统PID控制算法进行比较。为了使比较效果更清晰，对传统PID控制算法的控制参数也进行优化，其优化条件与IMNC的优化参数相同。在仿真实验中，均选用Matlab的GATOOL工具箱进行优化，初始种群中的个体数目是50，进化代数为500，参数搜索下限值均为0，初始范围均为［0，1］，其他参数为缺省值。优化控制参数如表1，2所示。

表1 传统PID控制方法的优化控制参数Tab.1 Op tim ized param eters of the conven tional PID

表2 IM NC控制方法的优化控制参数Tab.2 Optim ized parameters of the IM NC

图3(a)，(b)分别是控制对象A的工艺输出和控制器输出效果对比图。IMNC的上升时间、调节时间和超调量等性能指标，明显优于传统PID控制效果。控制器的输出比传统PID的控制输出要更加稳定。从图中可以看出，与传统PID控制相比，IMNC具有更好的控制效果。上升时间tr大约是35 s，σ%超调量约为0，调节时间ts约为113 s;同时也较好于文献［15］前馈PID控制效果tr=155 s，σ%= 5.5%，ts=200。图4(a)，(b)分别是控制对象B的工艺输出和控制器输出效果对比图。IMNC的上升时间、调节时间和超调量等性能指标，明显优于传统PID控制效果。控制器的输出比传统PID的控制输出要更加稳定。

从图4中可以看出，与传统PID控制相比，IMNC具有更好的控制效果。上升时间tr大约是28 s，σ%超调量约为0，调节时间ts约为36 s;同时也较好于文献［16］IMC-PID控制效果tr=30 s，σ%=5.0%，ts=60 s。从仿真结果可以看出，IMNC的控制性能均优于传统PID控制算法。

图3 对象A控制效果对比Fig.3 Com parison of the con trol effect for p lan t A

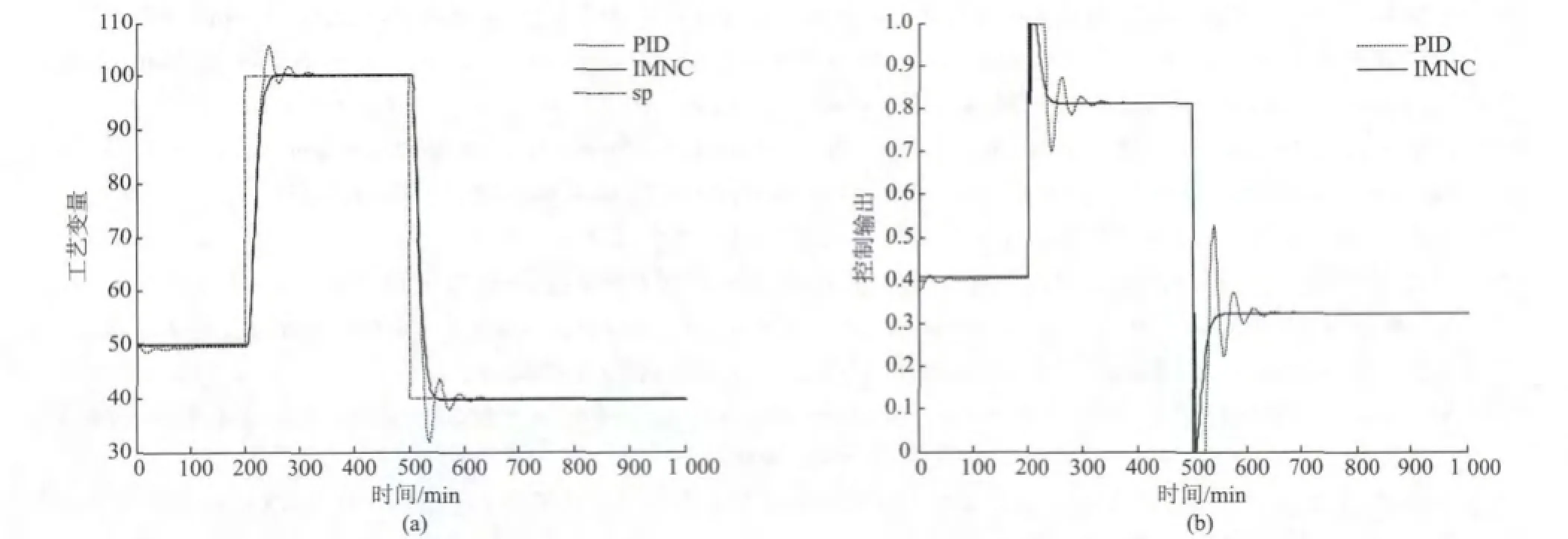
图4 对象B控制效果对比Fig.4 Com parison of the con trol effect for p lan t B

4 结语

基于控制系统的稳态控制增益，提出一种非线性脉冲控制体系架构及其控制算法。该非线性脉冲控制算法(IMNC)包括动态控制单元、稳态控制单元和协同输出控制单元3部分。其中动态控制单元主要担负动态变化过程的控制调节任务;稳态控制单元主要承担消除稳态变化过程的控制误差;协调输出单元则是根据控制系统的运行状态，负责协调动态控制单元和稳态控制单元的工作状态。最后选择大纯滞后和非最小相位控制对象，进行控制效果检验。仿真结果表明，IMNC的控制性能优于传统PID控制算法。该IMNC能够具有动态过程和稳态过程独立进行控制调节能力，动态控制单元和稳态控制单元独立性强，容易调整控制参数，对提高非线性对象控制效果具有一定的实际意义。

［1］张伟勇，黄德先，王毓栋，等.延迟焦化加热炉的自适应状态的反馈预测控制和专家控制［J］.中国化学工程学报:英文版，2008，16(4):590-598.

［2］刘智勇，尹征琦，刘焕成.冷热水混合系统的多变量专家控制［J］.信息与控制，2001，30(2):179-182.

LIU Zhiyong，YIN Zhengqi，LIU Huancheng.Multi-variables expert control for the cold-hot watermixer system［J］.Information and Control，2001，30(2):179-182.(in Chinese)

［3］ZHANG Hang，LUO Dayong.Application of an expert system using neural network to control the coagulant dosing in water treatment plant［J］.Journal of Control Theory and Applications，2004，2(1):89-92.

［4］郭冰洁，万磊，梁霄，等.水下机器人的S型模糊神经网络控制［J］.系统仿真学报，2008，20(15):4118-4121.

GUO Bingjie，WAN Lei，LIANG Xiao.S model fuzzy neural network control of underwater vehicles［J］.Journal of System Simulation，2008，20(15):4118-4121.(in Chinese)

［5］李树荣，薛秀莉，杨青.一类自适应神经网络控制器的设计［J］.中国石油大学学报:自然科学版，2008，32(1):138-142，151.

LIShurong，XUEXiuli，YANG Qing.Design of adaptive network controller for a class ofmultiple time-delays nonlinear system［J］.Journal of China University of Petroleum:Edition of Natural Science，2008，32(1):138-142，151.(in Chinese)

［6］DONG Zhenghong，WANG Yuanqin.Application of neural network inverse control system in turbo decoding［J］.Journal of Electronics(China)，2007，24(1):27-31.

［7］王宁，孟宪尧.输入采用一般模糊划分的T-S模糊控制系统稳定性分析［J］.自动化学报，2008，34(11):1441-1445.

WANGNing，MENG Xianyao.Stability analysis of T-S fuzzy control system with inputs using general fuzzy partition［J］.Acta Automatica Sinica，2008，34(11):1441-1445.(in Chinese)

［8］黄卫华.基于解析结构的模糊控制系统设计及稳定性分析［D］.武汉:武汉科技大学，2010.

［9］陈国洋，李柠，李少远.一类T-S模糊控制系统的稳定性分析及设计［J］.控制理论与应用，2010，27(3):310-316.

CHENGuoyang，LINing，LIShaoyuan.Stability analysis and design for a class of takagi-sugeno fuzzy control systems［J］.Control Theory and Application，2010，27(3):310-316.(in Chinese)

［10］王艳华.一类T-S模糊有记忆系统的保性能控制器设计［J］.沈阳师范大学学报:自然科学版，2014(4):486-490.

WANG Yanhua.Guaranteed cost controller design for a class of T-S fuzzy memory system［J］.Journal of Shenyang Normal University:Natural Science Ediition，2014(4):486-490.(in Chinese)

［11］ZHUWu，ZHANG Jiamin，LIU Hongli，et al.Fuzzy control on automatic frequency tracking of ultrasonic vibration system with high power and high quality factor Q［J］.Journal of Harbin Institute of Technology，2009，16(2):275-278.

［12］刘俊.一类T-S模糊控制系统的稳定性研究［D］.广州:广东工业大学，2011.

［13］杨青，李树荣，成玲.催化裂化装置的非线性预测控制［J］.中国石油大学学报:自然科学版，2005，29(3):139-143.

YANG Qing，LIShurong，CHEN Ling.Nonlinear model predictive control of fluid catalytic cracking unit［J］.Journal of China University of Petroleum:Edition of Natural Science，2005，29(3):139-143.(in Chinese)

［14］NIU Jian，XU Zu-hua，ZHAO Jun，et al.Model predictive control with an on-line identificationmodel of a supply chain unit［J］.Journal of Zhejiang University-Science C，2010，11(5):394-400.

［15］李东海，吴勇强，李立勤，等.特殊工业对象的PID控制系统仿真研究［J］.电子技术应用，2000，26(8):24-26.

LIDonghai，WU Yongqiang，LILiqing，et al.Simulation of the system of special industrial objects PID control［J］.Application of Eletronic Technique，2000，26(8):24-26.(in Chinese)

［16］马姝姝，陈夕松，杨俊.高阶时滞系统的降阶IMC-PID控制研究［J］.工业仪表与自动化装置，2010(2):3-5，11.

MA Shushu，CHEN Xisong，YANG Jun.Research on IMC-PID control for the complex time-delay system reduction［J］.Industrial Instrumentation and Automation，2010(2):3-5，11.(in Chinese)

(责任编辑:杨勇)

A Nonlinear Controller Based on Stable Control Gain

LIU Bao，DUAN Hui，WANG Junhong，ZHANGWenjie，KANG Zhongjian
(College of Information and Control Engineering，China University of Petroleum，Dongying 257061，China)

Based on the stable control gain，the system architecture of a novel impulse-nonlinear control(IMNC)is presented，and its control algorithm is provided in this paper.The IMNC includes dynamic control unit(DCU)，stable control unit(SCU)and cooperative output unit(COU).With the cooperative work of COU，the DCU can output a control impulse quick ly to improve the rise time，which may make the process variable approach the stable value rapid ly.The SCU can eliminate the control error based on the final stable output and combines the proportional or integral action to enhance the control accuracy.Finally，the large delay and non-minimal phase plants are selected separately to the examine IMNC＇s control performance.The simulation results indicate that the IMNC has better control performances than the conventional PID control algorithm.The IMNC is of practical engineering significance for improving the control effect of some comp lex control process.

control gain，nonlinear control，impulse control

TP 214+.2

A

1671－7147(2015)06－0717－06

2015－07－10;

2015－08－25。

国家自然科学基金重点项目(60534020;60775052);中央高校基本科研业务费专项项目(09CX04026A);山东省优秀中青年科学家科研奖励基金项目(BS2010DX038);教育部博士点新教师基金项目(20070425518);中国石油大学(华东)博士科研启动基金项目(Y070502)。

刘宝(1971—)，男，山东淄博人，副教授，工学博士。主要从事生物智能计算及控制研究。Email:lb314423@163.com