某大跨度斜拱桥吊杆张拉控制分析

穆怀天， 朱召泉 ， 李 欢

(河海大学 土木与交通学院，江苏 南京210098)

随着我国社会经济的发展，全国各地出现了各种采用吊杆作为传力结构的异型拱桥，称之为吊杆张拉拱式结构。这种受力方式使得拱肋的形式变得多样化。其施工的主要顺序为:先设置临时支架施工拱肋，然后再施工桥面系，最后通过张拉吊杆将桥面结构与承重结构形成一体。拱式结构内力通过吊杆张拉来传递，当吊杆索力满足设计要求时，结构的各项力学指标也相应地满足设计要求。

结构刚度较小的钢箱梁系杆拱桥在施工过程中，吊杆拉力的调整是十分重要的工作，各吊杆的最终拉力不仅直接关系到成桥的线形和成桥的受力状态，而且也直接影响着桥梁外形的美观和安全性能。但是各吊杆拉力的确定又是困难的工作，因为各根吊杆在每次张拉的同时会伴随着拱肋、桥面系主梁的相对位移，从而引起前期吊杆张拉力的松弛，呈现非线性变化，使得此类系杆拱桥的吊杆索力在张拉作业结束后难以达到设计要求。此外，索力的调整工作也很复杂，会严重影响到施工进度。所以整个施工过程中，正确确定吊杆张拉过程中各吊杆所需施加的预应力就显得非常关键［1］。

目前在桥梁工程吊杆张拉计算领域常用的方法有正装法、倒装法、无应力状态法和多次张拉的影响矩阵法［1］。国内外有很多学者对这个问题进行了研究与改进。

肖汝诚等通过广义影响矩阵概念，将斜拉桥优化的目标函数统一用索力变量与广义影响矩阵表示，导出斜拉桥索力优化的影响矩阵法。这种方法可用于施工阶段的索力优化和成桥后的索力调整;其又以静载弯曲能量代价最少原理来确定斜拉桥的合理索力，通过倒装法可以方便地确定斜拉索的施工张拉力［2］。

秦顺全院士成功地将无应力状态法应用于十多座大桥的施工控制。无应力状态法引出无应力曲率和无应力索长这个不变量及其计算方法，并利用该不变量准确地建立了施工过程和最终成桥状态之间的联系，使得施工过程中的受力和变形之间的关系更加明确［3］。

李洪波等通过研究确定了系杆拱桥合理的吊杆张拉力传统计算方法，提出基于影响矩阵法、综合刚性吊杆法和自动调索法来确定系杆拱桥的成桥吊杆内力的方法［4］。

1 工程背景简介

张家港市锦丰镇为打造以城市公园化为核心目标的综合性现代化生态新城，根据市政规划，在华山路往西跨越一干河位置建设一座人行景观桥梁［5］。一干河拟规划河道宽度为120 m，新建桥梁主跨采用105 m 的下承式异形钢拱桥，边跨约为12.5 m，桥梁的跨径布置为12.5 m + 105 m + 12.5 m，全桥共长131.94 m;桥梁范围内道路平面均位于曲线范围，曲线半径分别为29.1 m 和108 m;主梁以跨中为对称中心，采用双向人字坡;相对于人行桥，拱肋向外倾斜，倾斜角度为75°，拱肋拱轴线在其自身倾斜面内为二次抛物线，矢高为26.25 m，跨径为105 m，矢跨比为1/4，如图1 所示。全桥共有19 根吊杆，呈对称布置，由中间向两侧依次定义为DS1，DS2(2＇)DS3(3＇)，…，DS10(10＇)，如图2 所示。

图1 一干河人行景观桥立面Fig.1 Yigan river landscape footbridge elevation

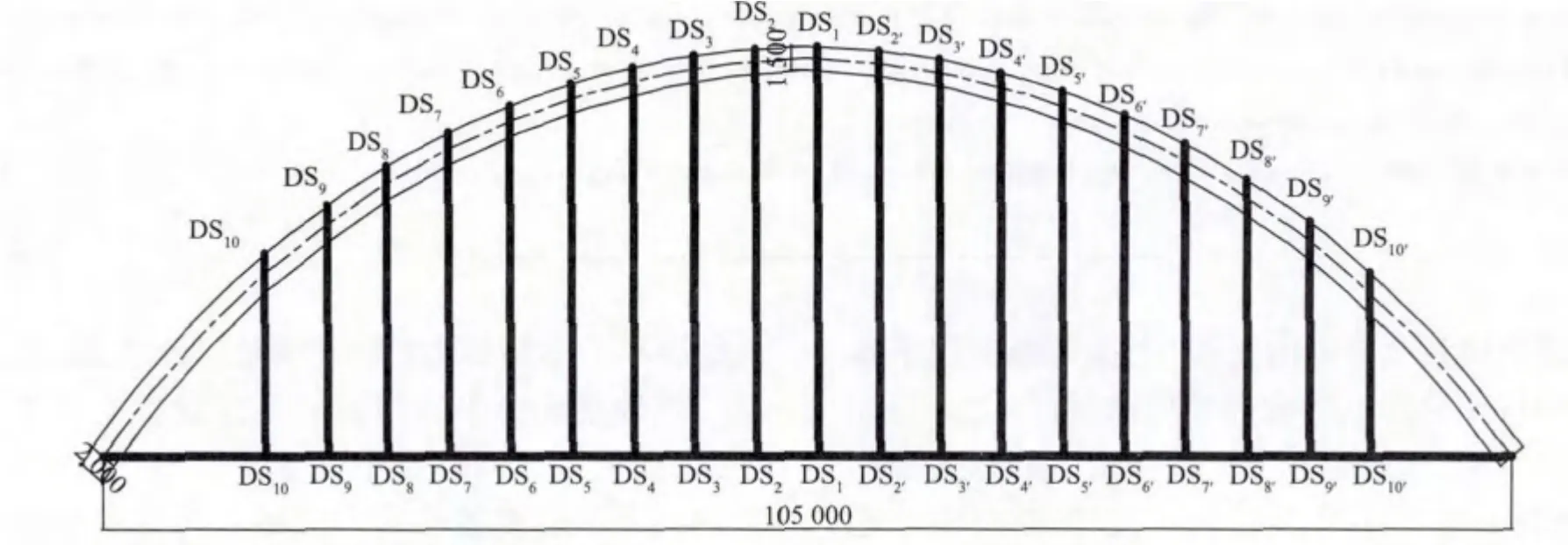
图2 吊索编号示意Fig.2 Schematic diagram of the sling

在施工中，吊杆是分批张拉的，由DS1开始依次向两侧张拉。由于一根吊杆的张拉会使整体结构发生变形，内力会重新分布，从而造成前期张拉吊杆的束力与后期张拉吊杆的束力之间相互影响，使得原本张拉好的吊杆产生应力松弛，达不到满足控制的束力条件。

而每一次新的调整又会产生新的内力重分布，这使得吊杆张力的调整变得非常繁琐［6］。因此有必要考虑在吊杆相互影响的前提下，通过计算确定张拉的顺序与张拉力的大小，使得完成一个阶段的张拉后，各吊杆均可达到此阶段的张拉设计值，不必进行调整［7］。

2 Ansys 建模与倒装法控制张拉力计算

2.1 Ansys 建模

该大跨度斜拱桥的拱肋和桥面主梁均为钢箱型截面，有限元建模时，为提高计算精度，并使各单元的受力特性与实际结构一致，主拱、主梁、加劲肋、横隔板以及拱梁连接段均采用shell63 单元模拟;拱脚与基础预埋段内部密实灌注的混凝土采用solid65 单元模拟;吊杆只能承受拉力作用，故采用link10 单元模拟，并设定KEYOPT(3)= 0;支架采用pipe16 单元模拟。拱、桥结构整体模型共划分为193 421 个节点，199 688 个单元。

2.2 倒装法控制张拉力计算

2.2.1 倒装计算法运算步骤

1)建立满足既定桥梁状态的有限元模型，如图3 所示。

图3 一干河斜拱桥Ansys 模型Fig.3 Ansys model of the Yigan river cable arch bridge

2)吊杆张拉次序按施工逆序进行计算。本桥吊杆施工张拉顺序为先中间(拱顶)后两边(拱脚)对称进行。按照施工方案吊杆张拉顺序的逆过程依次“杀死”相应的吊杆，从而获得当前状态下后续“杀死”吊索的张拉力。与该张拉力对应的就是按照桥梁的施工方案进行到当前状态时应当施加的吊杆初拉力［6］。

3)根据上述求得的吊杆张拉力对桥梁结构进行正序分析，判断所得的计算状态是否与步骤1)的既定状态吻合，如果不一致则仍需进行迭代计算，与此同时需对各施工阶段结构的安全性进行分析。

2.2.2 倒装计算法运算应用 根据设计方提供的成桥索力，利用倒装法依次逆向推导出铺装阶段的索力、实现桥面系脱架工作对应的索力以及拱肋脱架后的索力(模型计算中可通过改变结构对应阶段的自重来实现这一目标)，如表1 所示;并且运用倒装法确定了初张拉时各吊杆的张拉力来实现桥面系脱架这一重要施工环节。

表1 施工各阶段对应的索力理论计算值Tab.1 Calculated value of the cable force in theory

3 影响矩阵法控制张拉力的计算

3.1 影响矩阵法运算步骤

影响矩阵法的基本运算式表述为

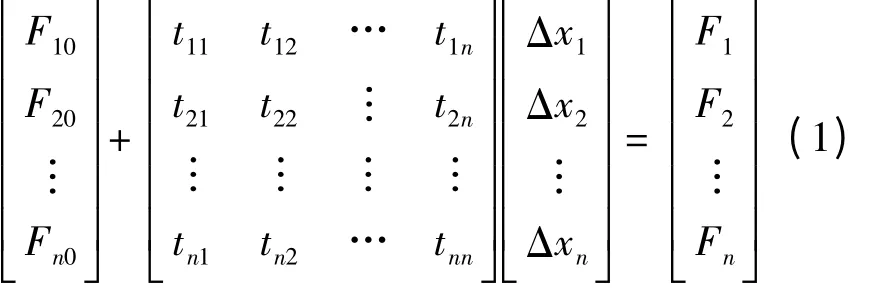
式中:［F10F20… Fn0］T为吊杆的初始索力［F1F2…Fn］T为吊杆的目标索力;［Δx1Δx2… Δxn］T为张拉力增加值(基本未知量);tij为第j 号吊杆增加单位力时对i 号吊杆的影响，将这些系数组装后得到影响矩阵;n 为吊杆组数。

对于再张拉的情况，影响矩阵满秩，即式(1)存在唯一解。通过解线性方程组，可以得到［Δx1Δx2…Δxn］T，进而按下式求得施工张拉力［x1x2…xn］T:

上述方法基于一个重要的前提条件:所有的吊杆在张拉过程中都参与作用，即不存在压力松弛而退出工作的现象［8］。如果在理想的假定基础上求解的施工力使其他吊杆产生松弛时，把该松弛吊杆在计算模型中拆除，等到张拉该吊杆时，才将其加入到几何模型中，形成新的影响矩阵，再按式(1)计算张拉力。

如此循环，直到所有的吊杆都不存在松弛现象。影响矩阵法多用于处在线性状态的结构，且结构体系、约束情况保持不变，而对于结构体系不断变化的初张拉(桥面系未脱架)情况并不适合。

3.2 影响矩阵法计算吊杆张拉控制力

待桥面系护栏安装及混凝土浇筑作业完成后，通过索力测试仪测出DS1至DS10(10＇)的索力分别为173.9 kN，178.0 kN，172.5 kN，173.3 kN，156.7 kN，160.2 kN，183.0 kN，212.5 kN，192.8 kN，209.4 kN。对照吊杆张拉力的设计值，采用2 台千斤顶由中间到两端对称张拉，以消除索力差值。张拉顺序为:DS1→DS2;DS2'→DS3;DS3→DS3'→DS4;DS4'→DS5;DS5'→DS6;DS6'→DS7;DS7'→DS8;DS8'→DS9;DS9'→DS10;DS10'。

3.3 原始刚度矩阵的建立

首先建立处于上述索力的原始计算模型，然后按照上述张拉顺序对吊杆进行张拉，每次张拉后恢复原始模型，再张拉下一对吊杆。在具体操作计算中，将张拉力的增量设定为20 kN，然后将矩阵每个元素除以20，由此可得到影响矩阵各系数见表2所示。

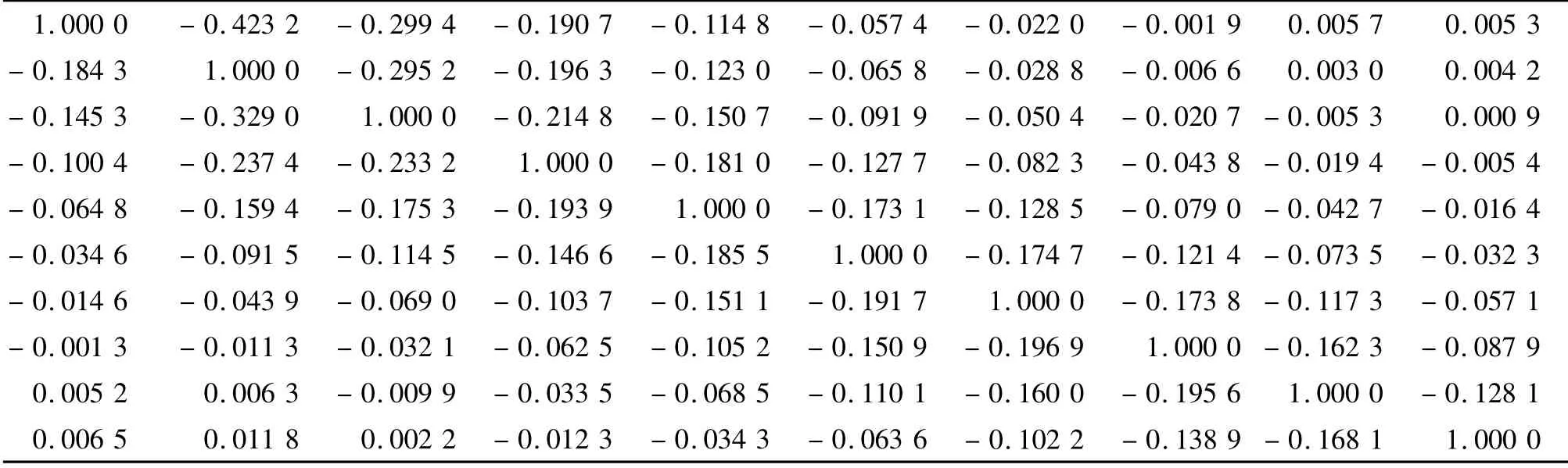
表2 初始影响矩阵系数Tab.2 Initial influence matrix coefficients

根据索力实测值［F10F20…F100］T= ［173.9 178.0 172.5 173.3 156.7 160.2 183.0 212.5 192.8 209.4］T;索 力 控 制 值［F1F2…F10］T= ［209.0 205.0 193.0 204.0 183.0 181.0 194.0 202.0 196.0 215.0］T;按照式(1)，利用Matlab 语言按Jabobi 迭代算法求解此10 阶线性方程组，初步计算结果为［Δx1Δx2…Δxn］T= ［598.2 501.6 530.7 532.5 504.9 446.9 385.7 297.4 245.3 168.9］T。为了满足吊杆在张拉过程中都参与作用的重要条件，检验Δxi(i = 1，2，…n －1)，若则令i = i +1 继续进行检验，直到全部满足条件;相反，若得到，则需令Fi，0=0，ti+1，1= 0，ti+1，2= 0 …ti +1，i = 0 代入方程组重新计算［Δx1Δx2…Δxn］T。

经过多次修正后最后影响矩阵系数修正如表3所示。

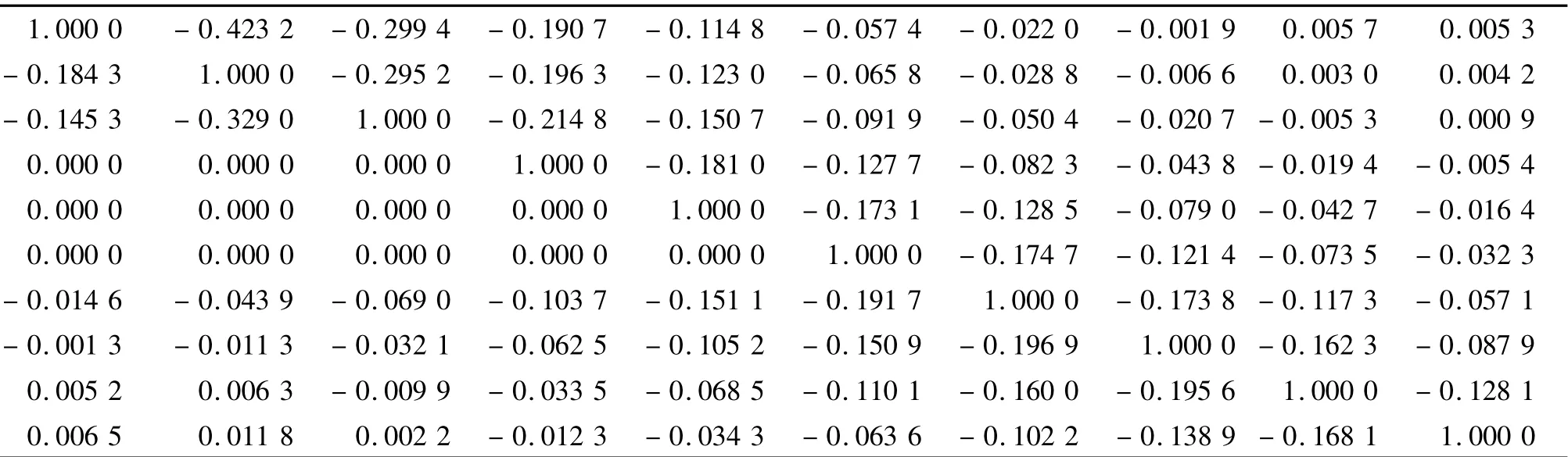
表3 修正后影响矩阵系数Tab.3 Modified influence matrix coefficients

代入式(1)重新计算求得各吊杆张拉力增加值［Δx1Δx2…Δxn］T= ［375.9 312.5 326.7 316.1 277.3 254.8 227.8 168.0 142.1 98.9］T，然后根据式(2)求得实际张拉过程中各吊杆的张拉力［x1x2…xn］T= ［549.8 421.2 341.7 316.1 277.3 254.8 245.5 233.8 208.7 215.0］T。

按上述计算所得索力和张拉顺序张拉吊杆，最终所得索力实测值与设计值对比结果如表4 所示。

表4 张拉力结果对比Tab.4 Results comparison of tensile force

从表4 数据可以看出，成桥状态的实测索力和目标索力最大差值出现在首次张拉的DS1位置，末次张拉的D10、DS10'索力和设计值最为接近，因为后期张拉的吊杆会对前期已完成张拉的吊杆产生影响;最大误差百分数为8.04 ＜10，满足相关技术的要求。

4 结 语

以一干河上修建的大跨度钢箱梁斜拱桥为例，分别利用Ansys 与Matlab 软件，采用倒装法与影响矩阵法分别计算了吊杆在不同工况下的张拉力。在倒装法中，利用软件的“生死单元”高级技术依次逆向推导出铺装阶段的索力、桥面系脱架工作阶段的索力以及拱肋脱架后的索力，配合施工方完成了吊杆的初张拉及桥面系主梁的脱架工作。

桥面护栏安装和混凝土浇筑作业完成后，利用DH5906 无线索力测试仪采取振动频率量测法进行索力监测，根据索力实测值与设计值间的差异，利用影响矩阵法，通过简单的回代方法求出施工过程中每根吊杆对应张拉顺序的控制值，从而对吊杆张拉力进行实际控制，并最终完成成桥阶段的调索工作。

在吊杆张拉控制方面，利用倒装法和影响矩阵法的分析结果实时监控，大大缩短了施工时间，节省了施工费用，为此桥安全顺利的施工提供了可靠的技术支撑。

［1］孙九春.拱式结构吊杆张拉索力计算方法综述［J］.结构工程师，2010，26(4):154-159.

SUN Jiuchun.Calculation method of cable force of arch structure［J］.Structural Engineer，2010，26(4):154-159.(in Chinese)

［2］杨俊.基于影响矩阵的大跨桥梁合理成桥状态与施工控制研究［D］.武汉:武汉理工大学，2008.

［3］刘智芳.台风区大跨度钢桁架拱桥施工控制关键技术研究［D］.广州:华南理工大学，2014.

［4］李洪波，马玉全，于天龙.基于影响矩阵的系杆拱桥合理成桥吊杆索力确定［J］.科学技术与工程，2009(10):17-19.

LI Hongbo，MA Yuquan，YU Tianlong.Determination of rational completion hanger force of bowstring arch bridges on the basis of influence matrix method［J］.Science and Technology and Engineering，2009(10):17-19.(in Chinese)

［5］李欢，朱召泉，朱瑞虎.某大跨度斜拱桥施工仿真分析与对比［J］.低温建筑技术，2014，36(10):88-91.LI Huan，ZHU Zhaoquan，ZHU Ruihu.Construction simulation analysis and comparison of a large span obligue arch bridge［J］.Low Temperature Architecture Technology，2014，36(10):88-91.(in Chinese)

［6］李新平，钟健聪.空间系杆拱桥吊杆张拉控制分析［J］.华南理工大学学报:自然科学版，2004，32(7):89-92.

LI Xinping，ZHONG Jiancong. Control analysis of the tension in suspenders of a spatial tied-arch bridge［J］. Journal of South China University of Technology:Natural Science Edition，2004，32(7):89-92.(in Chinese)

［7］钟健聪，李新平.空间系杆拱桥吊杆张拉控制的研究I［J］.广东公路交通，2004(2):1-4.ZHONG Jiancong，LI Xinping. Research on control of tensions in suspenders for a spatial tied-arch bridge［J］. Guangdong Highway Communications，2004(2):1-4.(in Chinese)

［8］孙九春.影响矩阵法在吊杆张拉计算中的应用［J］.中国市政工程，2009(5):19-21.

SUN Jiuchun.On influence matrix method applied in the suspender tension computing［J］. China Municipal Engineering，2009(5):19-21.(in Chinese)