向量在解决有关“距离”问题教学时的思考

新疆伊宁市第三中学 彭吉成

向量在解决有关“距离”问题教学时的思考

新疆伊宁市第三中学 彭吉成

向量在解决有关“距离”问题的优势 ：思路简洁,计算量少。

向量 距离 解题思路

向量是一个“数形结合体”，它在证明“平直关系”、解决平面或空间中的角的问题时非常简便，人教版的教材对此进行了详尽阐述，但教材对于用向量解决“距离”的问题涉及很少。而向量在解决这些问题时也有独到之处，向量知识在许多国家的中学数学教材中早就成了一个基本的教学内容。

在我国全面实施新课程后，向量虽然已进入中学，但仍处于起步的阶段。向量知识、向量观点在数学、物理等学科的很多分支有着广泛的应用，它具有代数形式和几何形式的“双重身份”，融数形于一体，与中学数学教学内容的许多主干知识综合形成知识交汇点。而在高中数学体系中，解析几何、立体几何均占有很重要的地位，有些问题用常规方法解决往往比较繁杂，不妨利用向量简化过程。但实际情况是很多学生在学习中不会应用向量解决数学问题，应用向量的意识不强。在高中数学新课程教材中，学生学习平面向量在前，学习解析几何、立体几何在后，而且教材中二者知识整合不多，很多学生在学习中就“平面向量”解平面向量题，不会应用平面向量解决几何问题。正因为如此，教师自身首先要深入研究这类问题，通过教师的引领作用，教会学生这样思考，用这样的思路解决数学问题。

本文结合两个具体的实例予以解释说明向量在解决解析几何、立体几何问题时，所展示出的简洁之美。

一、向量解决平面内点到直线距离的问题

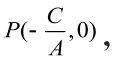
示意图

人教版必修二教材在证明这个公式时思路很简洁，但繁琐的计算令人望而生畏，而向量解决这个问题从思路到运算都很简洁。

二、向量解决空间中点到直线的距离的问题

从一个具体的例子出发，其他的各种情况下思路完全相同。需要说明的一点是应用向量解决问题时，往往首先要建立平面或空间直角坐标系，有了向量的坐标，向量的威力才能充分地发挥出来。

例题：在长方体ABCD-A1B1C1D1中，AB=1，AD=2, AA1=3,求点A到体对角线A1C的距离d。

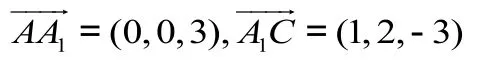
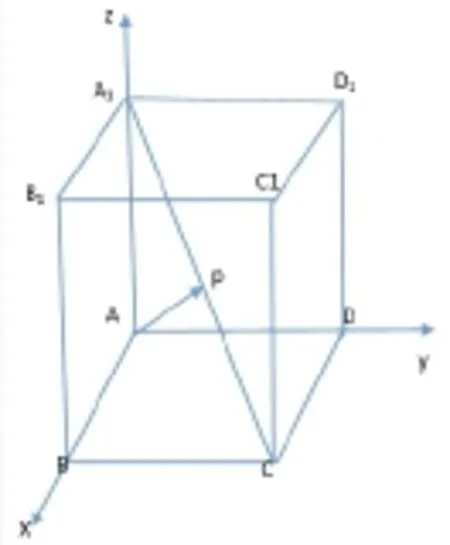
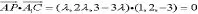
∴λ+4λ-9+9λ=0

由此可见，因为向量具有几何形式和代数形式的“双重身份”，使向量与解析几何、立体几何之间有着密切联系，而新课程高考则突出了对向量与几何结合考查，这就要求我们在平时的几何教学与复习中，应抓住时机，有效地渗透向量有关知识，树立应用向量的意识，那么如何树立应用向量的意识，我认为应从如下几点考虑：

1.如何树立应用向量的意识，在教学中应先从学生熟悉的平面几何问题入手，让学生体会向量的工具性。

2.如何树立应用向量的意识，应充分挖掘课本素材，在教学中从推导有关公式、定理，例题讲解入手，让学生去品味、去领悟，在公式、定理的探索、形成中逐渐体会向量的工具性，逐渐形成应用向量的意识。

3.如何树立应用向量的意识，在教学中还应注重引导学生善于运用一些问题的结论，加以引申，使之成为解题方法，体会向量解题的优越性。

4.如何树立应用向量的意识，还应该有意识的要求学生比较向量方法和传统方法，到底孰优孰劣，一旦学生体会到向量简洁的优势，他们就能自动形成一种自觉。

随着教学改革的逐步深入，今后对于向量与其他知识的综合考察不仅不会弱化，而且肯定会进一步加强，向量作为数形结合的有力工具，成为了联系众多知识的桥梁，因此，向量与三角、解析几何、立体几何的教汇仍是今后一段时间高考命题的必然趋势，所以必须高度重视对向量的复习和演练，直到达到深刻理解、运用熟练的境地。

ISSN2095-6711/Z01-2015-08-0140