让有效操作与思维发展相生相伴

宗建华

数学是一门抽象性、逻辑性很强的学科，而小学生的思维正处于由以具体形象思维为主向以抽象逻辑思维为主过渡的阶段，它们的平衡点在哪里？笔者以为，动手操作活动可以是在数学知识的抽象性和学生思维的形象性之间架起的一座桥梁。不久前，笔者在常州的一次研讨活动中，听了两节课。在这两节课中，教师都精心设计了动手操作的环节。

案例1 四年级下册《三角形的认识》

教师通过学校、电影院、少年宫三点之间某两点走哪条路最近，引导学生初步感悟三角形的三边关系之后，讨论得出，这样的三角形路线中，“走任意两条边的路都比走一条边的路长”，教师随即不完全归纳“在三角形中，任意两边的和大于第三边”。接着进行了如下教学。

问：如果两边之和小于或等于第三边，还能围成三角形吗？

组织学生用9厘米、5厘米、3厘米和9厘米、6厘米、3厘米的两组小棒操作。

学生操作。

师：谁来说说你的发现？

生：我发现3厘米、6厘米、9厘米这三根可以围成一个三角形。

师：哦，能围成？其他同学呢？

大部分同学说能。

师感到有点意外，于是请这位同学到实物投影仪上演示一下。

学生在展台上小心地操作，结果就像他所说的那样，的确围成了一个三角形，如图。

师：这种围法有什么问题吗？

学生面面相觑，没有什么问题啊！

师（赶紧解释）：这个三角形没有首尾相连，两边短了些。

为了证明不能围成，教师接下来通过课件进行了演示，但效果并不好，很多学生始终没有明白教师的意思，接下来三角形三边关系完整结论的得出也就显得牵强附会。

案例2 三年级上册《两位数除以一位数的除法》

特级教师王凌老师执教的《两位数除以一位数的除法》一课，设计了分小棒的操作活动。

（活动一）分一分1

40÷2=

你是怎样算的？说一说。

用小棒分一分。

（活动二）分一分2

根据情境，发现信息提出问题，解决46÷2=？，引导操作，用小棒分一分。学生先独立分，再说一说是怎样分的？先分多少？再分多少？接着教师再用课件演示一遍分小棒的过程。

适度强化：分一分 36÷3 48÷4

理清算理，明确先分几个十，再分几个一的顺序。

（活动三）看一看，算一算。

42÷2

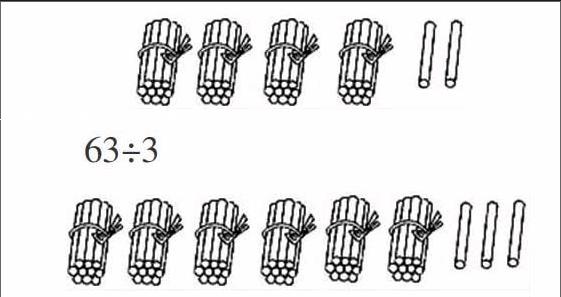
63÷3

不动手操作，看着小棒图，在头脑中想一想分的过程，找出得数。

（活动四）想一想，算一算。

88÷4 26÷2

离开小棒，看着算式想先算什么，再算什么，合起来是多少。

原本以为用二年级学生上三年级内容，学生会遇到很多困难，但王凌老师的课堂气氛很活跃，学生学得很轻松。

以上两个教学片段，教师都在新知的探索环节引导学生动手操作，但所产生的教学效果却迥然不同。细细分析，启示有二：有效的操作是途径，思维的发展是根本。

1.精心组织，有效操作，方能为思维发展插上翅膀

案例1中教师在学生初步得出三角形的三边关系后，利用反证的方法引导学生思考：如果两边之和等于或小于第三边还能否围成三角形？教师的意图很明显，希望通过正反两方面的验证来帮助学生形成比较完整的对三角形三边关系的认识。但实际情况是由于教师缺乏对整个操作过程的精心组织，没能在选取材料时关注细节，所提供给学生用塑料吸管做成的小棒，有一定的宽度，再加上学生操作的精细程度不够高，导致学生用3厘米、6厘米、9厘米的三根小棒围成了一个他们认可的三角形，从而影响了学生对三角形三边关系的感悟和探索，可以说对学生思维的发展也是有限的。其实，这里教师可以为学生提供两端稍微尖一点的小棒，并在每一根小棒上贴上它的长度的标签，这样既可以避免误差，又使操作更直观，便于规律的发现。

“儿童的智慧在他们的手指尖上。”数学课堂上，学生通过自己动手操作，体会到了创造的乐趣，体验到了成功的喜悦，同时促进了思维的发展，但前提是这样的操作活动必须是教师课前精心预设的，是经过教者深思熟虑的。尤其要关注的是，动手操作有别于课堂上的其他教学活动，在这个过程中，由于操作时机、个体、素材等方面的原因，往往会产生很多意想不到的情况，这就要求教师要有更高的课堂驾驭能力，课前要对学生操作活动的各个环节用心预设，想到可能产生的各种情况，心中有预案，对意外情况能因势利导。一次操作活动，如果能激发学生探究的欲望，能提供符合学生特点的实用操作材料，能对活动过程有效监控，因势利导，我想是可以避免出现案例1那样的情况的，也是可以真正促进学生思维发展的。反观案例2，教师选择了恰当的活动时机，让学生动手、动脑，避免那种为了操作而操作的无效活动，操作活动组织得有序而有层次性，操作与思维相伴。这样的课堂动手操作活动，有效、扎实，它能真正为学生的思维插上翱翔的翅膀。

2.用心引导，逐步抽象，更应让直观操作最终走向思维操作

不可否认，动手操作作为一种形象、直观和生动的学习方式，深得学生和教师喜爱，教学中如果应用得当，能促进学生对知识的理解，激起学生的数学思考，有利于数学问题的解决。但如果只停留于直观操作，不让学生触及一些抽象、理性的学习方式，是不利于学生思维发展的。我们的最终目的并不是为了操作而操作，而是希望在这个过程中学生用手去操作，用心去观察，用脑去思考，从直观到抽象，最终从直观操作走向思维操作，真正促进学生思维的发展。

王凌老师的课堂给了我们很好的启示，《两位数除以一位数的除法》这节课整个探究过程由分小棒（直观模型）—想小棒（表象）—数的运算（符号操作）逐层铺开。先借助小棒分一分，帮助学生理清整十数除以一位数（40÷2）的算理，为下面的教学作了必要的铺垫。接着再类推到例题48÷2，继续让学生经历用小棒分一分的过程，这里着重让学生经历运算的过程，明确先分几个十，再分几个一的运算顺序，理清算理。之后组织学生看图，在脑子里分一分，再到无图光看算式说一说，从具体直观到抽象思考，引导步步深入。

王凌老师的课充分发挥了动手操作在促进知识的理解、帮助问题的解决方面的作用。通过动手操作，引领学生经历问题的探究过程，理解了两位数除以一位数的算理。不仅如此，在学生建立直观模型后，王老师对这一模型进行了逐步抽象，看图在脑子里分一分、无图看算式说一说这一过程堪称精妙而又水到渠成，既引导学生经历有效的数学抽象过程，完成感性认识到理性认识的提升，又注重这一过程的层次性，自然流畅地完成了由直觉动作思维—具体形象思维—抽象逻辑思维的过渡。在学习中，学生不仅对“两位数除以一位数”的算理、算法理解得更加深刻，而且初步学会了探究，学会了学习。这样的课堂，孩子真正玩得开心、学得透彻。

再来看案例1的教学，既然思维的发展是动手操作最终的归宿，笔者以为教师可以强化“两边之和小于第三边”的情况，以此为突破口，只选择三边分别是9厘米、5厘米、3厘米这种情况，摒弃形式上的动手操作，通过教师的设问：“如果两边之和小于第三边，它们还能围成三角形吗？”激起学生的认知冲突，引导学生先在头脑中想想。要相信学生，很多孩子不借助小棒的直观操作，也可以通过生活经验想清楚不能围成三角形的原因，真正想通了这点，对“两边之和等于第三边”的情况，也就迎刃而解了。

总之，数学课堂上，合理把握动手操作的时机，精心组织操作活动，能在数学知识的抽象性和学生思维的形象性之间真正架起一座桥梁，能为孩子的思维发展插上翅膀。而在动手操作中善于挖掘思维参与的深度，让直观操作最终走向思维操作，是数学学习的核心所在。？筻endprint