重视培养学生归纳推理,让归纳和演绎比翼双飞
2015-01-14李峤
李峤


什么是“数学的基本思想”?史宁中教授认为:数学思想不仅包括学习数学知识所涉及的思想,比如,等量代换、数形结合、递归、转换等,还包括解数学题所涉及的合并同类项、配方法、换元法等。“基本思想”主要是指演绎和归纳,在具体的问题中,会涉及数学抽象、数学模型、等量代换、数形结合等数学思想,但最上位的思想还是演绎和归纳。演绎推理是根据概念、定理等按照规则进行的推理,是一种由一般到特殊的推理,它的主要功能在于验证结论。归纳推理正好与演绎推理相反,它是一种从特殊到一般的推理,包括枚举、归纳、类比、统计推断、因果分析以及观察实验、比较分类、综合分析等,它的主要功能在于发现新的真理。
从笔者长期处于教学第一线的体会来看,教师往往更注重演绎推理的渗透,而忽略归纳推理(也叫合情推理)能力的培养。的确,在教学面积、体积公式的推导,运算定律,比的基本性质,等等内容时,教师可能都会让学生尝试先猜测再验证。有些教师就认为这已经是向学生渗透猜测验证的思想方法,但是,从根本上讲,归纳推理作为与演绎推理同等重要的基本数学思想,也仅仅是在学习新课的过程中给学生渗透而已,而一旦新课讲完,开始练习,归纳推理就基本“拜拜”了。也就是说,不管是教学,还是作业考试,其实根本上还是清一色的演绎推理。因此笔者针对此现象做了思考与教学实践。
一、学生与生俱来的归纳推理的“火苗”不应该被扼杀
【案例1】数学兴趣小组一共有15名同学,其中男生有9名,女生有多少名?
学生列式“9+6=15”,然后给出答案:女生有6名。面对这样的算式,很多教师往往是粗暴地判错了事。
笔者认为,我们应该充分肯定和保护学生这样的想法甚至书写方法。我们有时为了追求一些外在的东西,而用格式、规定等去扼杀了很多有创意的东西,其实这样写又有何不可呢?从思维上讲,是考虑9名男生和几名女生才能凑成15人,这是多好的代数思想的萌芽呀!学生在头脑中可能经历了9+4、9+5等过程,这又何尝不可呢?有人要问:“15-9=6要不要教?”要教,但是两者并不矛盾,因为这是两种不同的想法和解题方法。
二、在练习中培养学生归纳推理的能力
有的教师注意在新课环节渗透归纳思想,但是一旦新课学完,练习就成为对知识点的反复巩固,最后的落脚点仍然在知识点上。笔者认为这样是不够的,事实上学生从练习中汲取的营养甚至会多过新课环节。练习时,学生经历比较独立的读题审题、思考尝试的过程,对于这个过程中所经历的东西会有更深刻的理解和感悟。所以,教师应该在这个环节提供给他们感受归纳推理的平台。
1.重视归纳的过程而非结果
在小学阶段,很多练习题中可以总结归纳出一些规律性的东西,教师会引导学生去归纳,但更多的是让学生去记忆这些结论性的东西,以应对考试。实际上死记硬背既费力且没什么效果,如果不能理解,就算背得好都不会用,而要想理解得更好,就应该在归纳的过程下更多工夫。
例如人教版五年级上册P24第3题和P25第8题:
■
这两题很显然都是要让学生总结并发现规律,教师肯定也是这样做的。但这里要强调的是,应该给予学生足够的时间,并在方法上指导他们,让他们自己去尝试归纳总结出规律,而不是教师迅速地抛出规律,让学生去记忆,然后不停地使用规律去练习。这样的例子在人教版的教材中非常多见。
2.突出归纳推理的优点
教材中有些内容可用多种方法呈现,这时教师就可以从多方面制定教学目标,譬如选择某些内容为载体,有意识地、刻意地突出和体现重要的归纳推理的思想方法。
例如人教版六年级上册数学广角的“鸡兔同笼”,教材呈现了表格法、假设法、代数法(“你知道吗”还介绍了“抬脚法”),那么教师在教学时就可以根据自己的教学目标去进行取舍。
经过教学实践的检验,假设法是解决这类问题比较巧妙的方法,但是假设法有它的局限性,并且学生不易理解,学过之后就忘了,最后就只剩下列方程的一般代数法。代数法具有很强的一般性,但是作为数学广角的内容,如果简单地用代数法去处理,教材的编写者把它放到用方程解决问题单元岂不是更好?这显然就和“数学广角”的设计思想不符。到底是什么方法更有一般性,适用范围更广泛,更能体现数学的基本思想?基于这样的思考和教学实践,教师应该让学生通过列举的方法进行尝试,在尝试的过程中不断猜测并发现规律,从而优化探索的过程。这种尝试、列举、验证的方法就是解决很多问题经常采用的方法,是数学中最朴素并且广泛应用的方法,也渗透了最基本的数学思想。
因此归纳推理成为这堂课学生最需要感受的思想。于是笔者引导学生先随意猜测鸡和兔的只数,然后验算出此时鸡和兔的脚数,再与实际的脚数进行对比。学生会发现,脚数少了就应该增加兔的只数,脚数多了就应该增加鸡的只数,从而调整他们的猜测。这个层次的内容,从笔者近四年的教学实际情况来看,几乎100%的学生都能掌握运用。而有部分思维好的学生,会进一步发现:可以把第一次猜测的脚数与实际脚数进行比较,用相差的总脚数去除以一只鸡和一只兔相差的2只脚,从而一次性找到应该如何调整鸡和兔的只数的方法。这样的教学过程,强烈地改变了学生的认知,拓宽了他们解决问题的方法。笔者是在六年级接手一个班的教学,刚开始的时候学生一遇到问题,只会想如何去列式计算,而经过这个内容的教学,至少有超过一半的学生对于归纳推理有了更深刻的认识,并能恰当地去应用。
例如:画一个周长为32cm,长和宽的比是3∶5的长方形。
以前学生只会按部就班地用按比分配的方法去求出长方形的长和宽,然后再画图。现在很多学生会从3∶5这个条件出发,(3+5)×2=16,(6+10)×2=32,从而找到答案。这种认识上的进步是令人欣慰的。
例如:(1)画一个面积为48cm,长和宽的比是3∶4的长方形。endprint
(2)做一个底面积为36平方厘米、高为5厘米的长方体框架需要多少厘米的铁丝?
这样的题目以前是学习的难点,而现在学生自然就会想到用合情推理的方法去解决问题,这些问题也就成为绝大多数学生都能够解决的问题。这应该就是归纳推理发挥作用的体现吧!
3.鼓励学生用归纳推理的方式去解决问题
有了教师的引导和鼓励,学生的思维也打开了,他们做题时不再局限于演绎推理的方法,作业中大量地出现归纳推理的思想方法。例如:
1.中国农历中的“夏至”是一年中白昼最长、黑夜最短的一天。这一天,北京的白昼时间与黑夜时间的比是5∶3,白昼和黑夜分别为多少小时?
5∶3=10∶6=15∶9,
5+3=8,10+6=16,15+9=24。
答:白昼有15个小时,黑夜有9个小时。
2.做一个底面积是36cm2,高为4.5cm的长方体框架,至少需要多少厘米长的铁丝?
1+36=37,2+18=20,3+12=15,
4+9=13,6+6=12。
因为12最小,所以(6+6+4.5)×4=66(cm)。
答:至少需要66cm。
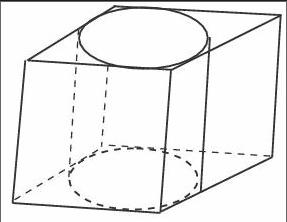
3.一个正方体的容器中(如下图所示)恰好能装入一个侧面积是12.56dm2的圆柱,这个容器的容积有多大?
■
12.56÷3.14=4(dm2),
2×2=4,
4×2=8(dm3)。
答:容积为8dm3。
4.东莞市某加工厂的甲、乙两个生产组承租了2010年广州亚运会吉祥物——“祥和如意乐洋洋”的一部分加工任务。甲组每天可加工200套,乙组每天可加工250套。甲组先加工了400套后,乙组才开始加工,乙组加工多少天后与甲组加工的同样多?
■
答:乙组加工8天后与甲组加工的同样多。
这些解题的方法,貌似离经叛道、不合规矩,但笔者不这样认为。作为与演绎推理同等重要的归纳推理,作为能培养创造性思维的重要思想方法,它值得起教师去“纵容和提倡”。更何况,这样去解决问题有理有据,思维过程清晰,答案准确,有什么理由去否定它们呢?
三、归纳与演绎并重更能促进学生思维的发展
归纳推理的核心,区别于演绎推理的最明显地方,就是要大胆地做出一些猜测和尝试,从错误中去分析推理,进而找到正确的结果或得出正确的结论。通过观察发现,女生回答问题,往往是确定或者至少自己认为是正确的才会举手发言,而有相当部分男生,想到什么就敢于表达什么。做题也是一样,从整体上看,男生更敢于动笔去尝试一些方法,因此涂涂改改也比较多;而女生更喜欢想清楚了再动笔,卷面清爽整洁。这里不谈其他,就从敢于尝试,从失败中得到启示这个角度去看,确实男生性格上的特点决定了男生在归纳推理方面能力更强,所以在创造性方面,很显然男生是领先于女生的。当然,这只是笔者就自己短短十来年教学过程中的观察而得出的思考,缺乏科学性,但归纳与演绎并重更能促进学生思维的发展应该是一个比较显而易见的结论。
小学都已全面使用新教材了。新教材是在2011版课程标准的基础上编排的,必将更有利于教师完成从“双基”到“四基”的转变。笔者特别希望的是,教师能够从观念上、从根本上更加重视与演绎推理同等重要的归纳推理,并且在学生的学习过程中去全方位地渗透,让学生能够有足够的机会感受归纳推理的“魅力”,会恰当地使用归纳推理去解决问题。
(责编 金 铃)endprint
