在“变题”中把思维引向深入
2015-01-14蒋明玉
蒋明玉

一、案例
在“圆的周长”的综合练习课上,笔者设计了下面这道题:求下列图形的周长(如图1)。
图1
在交流中,学生想到了以下这种思路,把“要求的周长”分成“两个部分”来思考(如图2)。
生1:细线周长:2π×4÷2=12.56(m);
粗线周长:π×4=12.56(m);
图形周长:12.56+12.56=25.12(m)。
图2
随着交流的深入,学生中有人提出了以下观点。
生2:既然细线部分长度等于粗线部分的长度,那么粗线的长度也等于大圆周长的一半(如图3),求“原来图形的周长”就可以转化成求“一个大圆的周长”。2π×4=25.12(m)。
图3
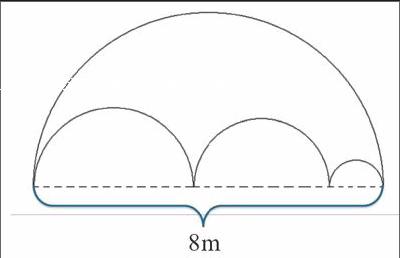
接着,笔者又将原题进行了适当改编,如图4。求下列图形的周长。
图4
生3:我猜想里面“三个小圆周长的一半”等于“大圆周长的一半”。
生4:我认为求“原来图形的周长”可以转化成“求一个大圆的周长。”π×8=25.12(m)。
师:如何验证这个猜想呢?
生5:设三个小圆的直径依次为d1、d2、d3,那么三个小圆周长的一半应该等于:
π×d1×+π×d2×+π×d3×=π×(d1+d2+d3)×
由于d1+d2+d3=8,所以π×(d1+d2+d3)×=π×8×,这样就可以发现:“三个小圆周长的一半”等于“大圆周长的一半”。由此发现,上面的猜想是正确的。
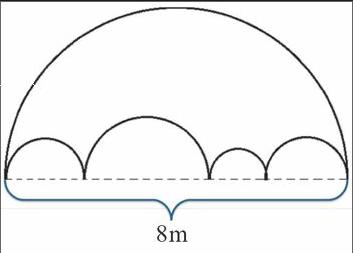
接着,笔者继续将题目改编成了如下的形状,如图5。求下列图形的周长。
图5
有了前面学习探究的基础,学生不难发现其中的规律,“这个不规则图形的周长”同样可以转化成“求一个大圆的周长”:π×8=25.12(m)。
二、反思
1.利用“变题”,突破了教学难点
通过“变题”的形式来设计题组,“形同质异”,这三道习题有一定的联系,更有比较大的区别。三道题的安排由易到难,数学思考的要求在逐步提高,难点在“变题”中逐步得到了突破。在探索规律的过程中,逐步培养学生学会“具体问题具体分析”的能力,有效克服死记硬背、就题论题等不良弊端,培养学生数学思维的灵活性和深刻性,使学生逐步做到举一反三,真正“知其然而又知其所以然”。
2.利用“习题组”,充分展现了规律的形成和发展过程
整个教学设计分成两个阶段,第1题的教学体现了“规律的形成”,第2、3题的教学则体现了“规律的发展”。通过展现规律的形成和发展过程来设计一组有联系的习题组,学生就可以多层次地探究问题,多角度地思考问题,同中求异、异中求同。从上例可以看到,数学教学要把“知识的形成和发展过程”展现给学生。“让学生看到思维过程”应是培养学生数学能力的有效途径之一。
(江苏省丹阳市华南实验学校 212300)endprint
