深入剖析错因 对症改进教法

田兴+钱建军

【摘 要】  小数乘法的算法是把它转化成整数乘法计算，最后处理积的小数点。其算理可以从两个角度分析，一是积的变化规律，二是计数单位的转化。理是说通了，但学生在列竖式计算时却经常犯困，他们不太能接受小数相乘在竖式中间过程中都变成了整数，而结果又变回了小数这样的过程。如果在列竖式时直接列成整数乘整数并推算小数乘法的结果，既不违背算理，还可以减少认知与书写中的许多麻烦。

【关  键  词】  小数乘法;以学定教;整数乘法;改进

【作者简介】 田兴，绍兴市柯桥区华舍小学，小学高级教师，绍兴县十佳青年教师标兵。研究方向：小学数学教育，学校行政管理。钱建军，绍兴市柯桥区华舍小学，中学高级教师，绍兴市教坛新秀。研究方向：小学数学课例研究。

中图分类号：G623.5 文献标识码：A 文章编号：1671-0568 （2014） 31-0120-04

一、问题的描述

“由教导学”或“以学定教”一直是教学研究的两条重要视线。现代教学论认为，教师的教学主导性应该建立在学生学习主体性基础之上，由“学法”研究“教法”可以使教学更加有效。我们通过研究错因，分析学情，有效确定教学的方法和策略，让学生从“未知”向“已知”自然顺利地过度。

笔者曾参加一次教研活动，听课内容是人教版五上年级《小数乘整数》，学生在练习时普遍出现这样的问题（如图1），教师讲道：小数乘整数的计算方法，是把小数乘法转化成整数乘法计算，最后再处理积的小数点，因此竖式计算的中间过程应该是两个整数，而不是像12.8那样的小数。随即要求学生把这个小数点擦去（如图2）。尽管这样强调，还是有不少学生在作业中出现了像图3类似的问题。

二、问题的分析

1. 学生访谈——不能自圆其说。为探明原因，笔者根据图3做了学生访谈。

师：中间过程你为什么还是在写小数？

生1：因为是小数乘法呀，我觉得写小数才算是小数乘法，写整数就不是小数乘法了。

生2：我觉得像图2肯定不对，128+32怎么可能等于44.8呢？

师：像你这样也不对呀，12.8+3.2也不等于44.8呀。况且你上下两个数位也没对齐，44.8怎么算呀。

生2：44.8我不是根据上面算出来的，而是因为因数3.2扩了10倍，所以积要缩小10倍。

从访谈中可以知道，学生的想法很简单，有一定的合理成份。但访谈也发现他们的思维角度是不一样的。有的学生观察竖式是从上往下，正是这种观察使他们觉得“有问题”。有的学生算出448后，不再理会计算过程了，根据推理得出结果。但当引导他们进行上下观察时，他们又觉得很不可思议，已全然不顾数位对齐的规则，很难自圆其说。

2. 教研组分析——峰回路转。在计算过程中还是出现小数是由于学生还不能够完全把小数乘法转化为整数乘法计算，这可能与教师的教学方法有关。我们依据的是运算概念，即积的变化规律进行教学的（教材示例如图4）。这样扩大、缩小的过程可能还是比较抽象的，我们是不是能想想别的办法。

经过分析与文献查阅，利用数概念教学也是一种办法，把一位、两位……小数进行单位换算，转化成几个0.1，0.01……的形式，这样小数乘法与整数乘法就上位统一了，他们都是在求“几个几”，只是计数单位不同而已。如像0.2×3就是2个0.1×3=6个0.1，再利用几何直观（如图5）学生必定把目光锁定在整数部分了。这样一种新的教学思路就形成了。

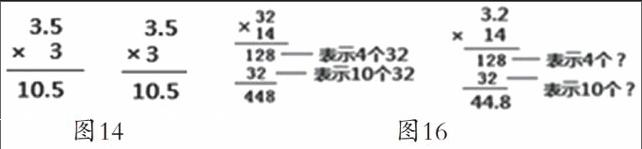
令人遗憾的是，教研组用第二种思路设计的教学，还是出现了老问题。我们把目光重新转回到教材给出的示例（图4）。结果中的3.60是对于乘数是一位数——“5”来说的，如果乘数“5”改为“15”，那么这个3.60作为0.72×15其中0.72×5的第一步过程，为什么就不可以了呢（图6）？5的前面多了一个1（实际为10），那就在3.60的基础上继续做下去，怎么就错了呢？我们觉得这种分析与前面的学生访谈就比较匹配了。教材中只给出了乘数是一位数的示例，3.60作为一个结果，学生很容易把它想成是两位数乘法中的一步过程。所以真正的问题不是在于“把小数乘法转化成整数乘法”，而是在于“乘数是一位数与乘数是两位数”在书写过程中的不同。因为所有乘数是一位数的“小数乘整数”学生都能做对，当变成两位数就错误百出了。

3. 深度追问——柳暗花明。造成学生心理困惑的根本原因是什么？不经意间，笔者听到了竖式笔算的过程口述，对“等于”、“横线”引起了注意。在学生心目中，竖式中的一条横线就是一个等号。在一步计算时，横式与竖式是一一对应的，许多教师就把0.72×5的竖式过程读成零点七二乘五等于三点六零，这样小数乘整数，结果还是小数。在两步计算中，0.72×15竖式过程（图7）写成了两个整数36 0与72，把这两个整数相加结果却“等于”一个小数（答案），在他们眼里是有违常理的。所以他们会非常自觉地在竖式过程中添上小数点以弥补心理的不安，即使是乱点小数点也总要比不点强。因此，出现像前面图3那样的错误也就不足为奇了。

那么竖式中的一条横线是不是“等于”符号？笔者访谈了几位教低年级的数学教师，他们都认为就是“等号”，以前在教学中他们都是这样说的。这种认识在一步计算时似乎发现不了问题，但两步以上的竖式问题就出来了。笔者在人教版新课标教材第三册教科书P 27找到了一个连加示例（图8）：如果竖式中的横线是等号，那么把竖式改写成横式就变成28+34=62+22=84，这也是学生常犯的一种错误，因为这三部分是不相等的，在连减或加减混合竖式计算中也如此。如果“_____”是“等号”，那么它应该有一种独立性而不是依附于某种“背景”。当我们把竖式中的各种成份都隐去，只剩下“_____”时，再让大家来认一认，恐怕没有人会认为它是“等号”了。看来这条横线只是表示一种间隔或是一种趋向（图9）。

三、在思考中不断改进

顺着上面的思路来，通过对比横式中的“连等号”，让学生重新认识竖式中“_____”这个符号的意义，对于突破教学难点似乎是一种办法。因为至少从理论上我们可以自圆其说了。但是对于刚学完四年级小数加减法竖式笔算升到五年级的学生，“小数点对齐”，“数位对齐”观念实在太根深蒂固了，实际上他们从二年级正式学加减法竖式时就开始有这样的强化了。即使是列一个普通的3.5×3的竖式，在他们的心目中也应该是3与3对齐。笔者也拿这个题目“考查”了办公室同事（有十年教龄的英语老师），她竟然也这样列式。况且依照上述的教学办法又会形成一个很有意思的怪论。0.72×15竖式计算我们一般是这样说的：把零点七二的零点（去掉）不看，记在心里，先用七十二乘十五，乘得的积缩小一百倍进行还原。再看四年级孩子解答多步计算题（图10-11），问他为什么这样算？他说先不去管15，把它记在心里，算出66后，再把它写出来。问五年级孩子解方程的第一步和第二步时“3”去哪里了？第三步怎么突然又出来了？他会说，我把3先记在心里了。 当四年级的时候我们不允许他把“15”记在心里，五上年级学小数乘法时，我们需要把小数记在心里，而后面单元的解方程，我们又不允许他把“3”记在心里了，学生简直是懵了。

在传统教学中，我们根据积的变化规律先得出44.8这个结果（图12），然后再去反思竖式的中间过程该怎么写，在这个环节中教师通常只能实行接受性教学，让学生记住书写规则。而这样的教学所带来的后果是学生在解释原因时，还是不明不白。只会讲“我们老师是这样说的”。

有效的教学行为应该是顺其自然，以学定教。笔者主张废弃小数乘法竖式笔算，直接用整数竖式计算，进而推算小数乘法结果（如图13），理由如下：

1.改进后的教法属于“老朋友解决新问题“，学生更觉亲近。对大量学生的调研表明，在没有任何教学暗示的前提下，不少孩子是可以用笔算“正确解答”一位小数乘整数的“积”，尽管上下位置对得不一样（图14）。在说明算理的时候他们也会自觉运用积的变化规律。并且统一用整数竖式笔算推算小数乘法结果，所用的数学思想方法也是转化，并没有发生变化。

2.改进后的教法思维与操作相和谐，视觉更清晰。对竖式的计算过程我们通常是通过横式进行算理分析的。例如在整数乘法的竖式过程中（如图13），32×14根据乘法分配律可以得到32×4+32×10=128+320=448，这个过程与竖式相匹配。但是当小数出现时，就变成似是而非了（图15）。从算理来讲，3.2×14=3.2×4+3.2×10=12.8+32，应该写12.8“却不让写”，这是条件算理与竖式过程不匹配。当两个“整数”相加却最后变成了小数，这是竖式过程与结果不匹配。改进后的教学方法避免了因思维与操作在视觉表现上过于胶着而带来的算理不清，计算过程显化、清晰。算到最后根据整数计算结果推算小数计算结果也是原来传统做法的必经之路，并没有增加难度。

3.改进后的教法更加突出数学本质。我们可以从单位转化的角度进行理解：3.2×14=32×0.1×14=32×14×0.1=32×14×0.1 原本的小数乘小数到最后就转化成了整数乘整数，然后再添加一个单位。

如果从积的变化规律角度进行分析，稍加点拨，学生就能自然地得出小数乘法的结果，这种能力表现为在横式推算上他们觉得更轻松。例如当告知32×14=448，要求如下答案，学生一般总能搞定： “ 320×14=  32×1.4=  3.2×14=  32×0.14=  0.32×14=   32×0.014=”一些中上生甚至可以在《小数乘整数》第一节课结束后就能推算像“3.2×1.4， 3.2×0.14”小数乘小数的计算结果。一道乘法算式能解决那么多的小数乘法题目，直接用整数乘整数解决小数乘法，更加可以突出数学本质。

四、写在最后

笔者根据这个观点进行教学设计，在多个班进行试教都比较成功。听课教师纷纷表示：

1.这样教学生是真懂了，以前的教学只是记住了教老师的要求。

2.这样做突出了心算，有一个好处是学生对于去掉小数末尾的0会更主动自然一些。如图17：当算出270以后，学生紧跟着是一步是除以10。这样原本末尾有0的答案都会因除以10，100…自动抵销掉。所以去掉小数末尾的0对于“教”的要求就少了许多。按照传统的教学，学生还会有一种非常典型的错误：先去掉了末尾的0，再添小数点。而按照本案教学，这种问题将不复存在。（这在笔者的课堂实践中得到了充分的证明）

3.考试怎么办？现行课本，作业本中还是传统的题目（如图18）那样，学生可能就不会做了。

笔者以为，教师有第3种顾虑是非常正常的。但进而反思一下，我们是不是可以不考这样的题目？当学生已经会解答小数乘小数的计算了，这样的考法还有意义吗？

多少年下来了，我们都是那样教、那样学的，难道“传统”不对？笔者无意“挑战”传统，只为帮助学生解开心中的那个谜团，为他们寻求“更适合学”的有效途径。

（编辑：陈诚）