模糊神经网络控制器在DMF回收系统的设计与应用

2015-01-13王华强程智超

化工自动化及仪表 2015年3期

王华强程智超

(合肥工业大学电气与自动化工程学院，合肥 230009)

二甲基甲酰胺(DMF)是一种用途广泛的化工原料，也是一种优良的溶剂，在合成革工业中被广泛用于合成革表面处理过程和二层皮湿法移膜表面处理工艺中。PU(聚氨酯树脂)合成革生产系统产生的废液中含有大量仅作为溶剂而未参与化学反应的DMF，因此DMF的回收处理很有必要。一方面可以解决含DMF的废液所带来的环境污染问题；另一方面回收的DMF可再利用为企业创造经济效应。DMF的回收属于典型的化工精馏过程，一般采用双塔或三塔精馏。回收的原理是利用废液中各成分(主要是水和DMF)沸点不同(常压下DMF沸点为152.8℃，水沸点为100℃)，通过对各个操作过程的温度进行控制，形成气液分离，从而达到提纯回收DMF的目的[1]。

笔者的研究对象为双塔式DMF回收精馏系统，DMF废液首先经过浓缩塔减压浓缩。浓缩塔塔压为负压，由再沸器供热，操作温度为75℃。精馏塔塔压可以为常压或略负压，通过导热油进行供热，操作温度为155℃。精馏塔的精馏段馏出物在冷凝器中冷凝成液体，进入回流罐，一部分回流到顶层塔板，以保持塔顶温度稳定；另一部分进入脱氨塔，进行脱酸处理，最后得到纯度相当高的DMF[2]。

精馏过程塔的温度是影响塔内气液平衡的重要参数之一，温度过高或过低都会影响产品的质量和生产效率。塔压的波动、进料流量和组成、回流量及再沸器的加热量等都会对塔的温度产生影响。在精馏塔温度控制系统中通过控制载热剂的流量来进行温度控制，是目前应用较为广泛的一种调节方式。

由于被控对象(塔温)在不同扰动作用下具有延迟性和惯性，仅使用单回路调节系统不能得到较好的调节品质，所以考虑采用串级控制策略。串级控制的抗扰动性能更好，能有效减小副回路的时间常数，从而改善被控对象的动态性能，而且串级控制具有一定的自适应能力，稳态误差较小。以精馏塔为例，其串级控制系统如图1所示。

图1 精馏塔串级控制系统简图

当系统中再沸器的出口汽温θ1发生变化时，副调节器就会通过执行机构来控制阀门，改变导热油量W，对汽温θ1进行粗调。主调节器通过检测灵敏板(精馏塔塔板中温度变化最灵敏的塔板)温度θ2与期望值比较，对副调节器进行校正，起到微调作用。串级系统中副回路的主要任务是迅速消除系统的各种扰动，故一般选用纯比例调节器，缩短控制过程的时间。主回路的任务是保持θ2的稳定，可选用PID调节器。其控制原理如图2所示。

图2 精馏塔温度串级控制原理框图

塔釜温度作为被控对象总是存在着比较大的延时，易产生偏差；影响被控对象的干扰因素很多；塔釜温度随时间和塔层的不同特性也不同，很难建立精确的数学模型。基于上述几点原因，笔者在原有的串级控制系统基础上采用基于模糊神经网络的PID控制器，提高对塔釜温度的控制效果[3]。

2 模糊神经网络控制器设计

神经网络和模糊系统都是非线性动力学系统，属于无模型的控制器，常用来处理不确定、非线性和其他不确定问题。但两者各有优缺点：模糊系统是通过模拟人的思维模式来进行知识的抽取和简单推理，但缺乏自学习和自适应能力；神经网络可以根据相应的样本进行有效的学习，能实现并行计算和信息分布式存储，同时具有较强的容错能力和自适应学习功能。但它不能很好地表达基于规则的知识，因此不能很好地利用已有的经验知识(一般只能取初始值为零或者随机值)，可能导致网络训练时间很长，网络训练陷入非要求的局部极值[4]。

2.1 模糊神经网络控制器总体结构

模糊神经网络就是将模糊系统与神经网络结合在一起，将模糊系统转换为对应的神经网络，从而提高系统的表达能力和学习能力。笔者设计的模糊神经网络控制器如图3所示。

NNI神经网络辨识器为模糊神经网络提供一个反传的校正信号，不断地对PID参数进行整定。PID控制器采用常规增量式PID控制器，其参数通过模糊神经网络进行设定。神经网络选用径向基神经网络(RBF)，RBF是一种局部逼近网络，能以任意精度逼近任意连续函数，在学习速度、逼近能力上都要优于常用的BP神经网络[5]。系统中

图3 模糊神经网络控制器结构框图

的模糊神经网络为二输入三输出结构：输入为温度的误差和温度误差变化率；输出分别为PID控制器的3个参数Kp、Ki、Kd。

2.2 模糊逻辑设计

输入量的模糊化。在进行模糊推理前需要将输入的精确量转化为模糊量。设系统温度控制目标为155℃±3℃，误差e和误差变化率ec对应的模糊语言变量为E和EC；Kp、Ki、Kd对应的模糊语言变量为ΔKp、ΔKi、ΔKd。E和EC的模糊子集均为{NB,NM,NS,ZE,PS,PM,PB}。ΔKp、ΔKi、ΔKd模糊子集均为{NB,NM,NS,ZE,PS,PM,PB}。根据线性变换法计算出实际偏差e对应的模糊值E，再根据隶属度函数计算出E属于模糊语言的隶属度。为计算方便，将输入输出量的模糊论域都设定为[-3,3]，隶属度函数均取高斯型函数。

模糊控制规则。模糊控制规则的设计是模糊控制器设计的关键，实质上是对操作工的实践操作经验的总结和利用。对于被控过程中不同的e和ec，操作人员凭经验总结出来对于PID参数Kp、Ki、Kd整定所遵循的几个原则：当e的绝对值较大时，取较大的Kp和较小的Kd可以使系统具有较好的跟踪性能，同时对积分作用加以限制(通常取Ki=0)，可避免系统响应出现大的超调；当e的绝对值处于中等大小时，Kp取值小些，Ki的取值适当，可使系统响应具有较小的超调，此时Kd的取值是关键，它对系统响应的影响最大，若ec的绝对值较大，则Kd取值小些，反之Kd取值大些；当e的绝对值较小时，Kp、Ki取大些可使系统具有较好的稳定性，同时若ec的绝对值较大，则Kd取值小些，反之Kd取值大些[6]。根据上述原则设计模糊规则见表1～3。

表1 ΔKp的模糊规则

表2 ΔKi的模糊规则

表3 ΔKd的模糊规则

模糊推理和解模糊化。模糊推理就是根据建立好的模糊规则和输入变量推理出模糊结果。一般形式为IF…THEN…。推理得出的结果是模糊量，需要通过解模糊化转换为清晰值。解模糊化方法有很多，这里采用最普遍的加权平均法。得到的清晰值并不是最终的实际控制量，还需要经过相应的尺度变换。采用线性变换法，公式如下：

(1)

式中ku——比例因子；

u——实际输出控制值；

u0——解模糊化得到的清晰值；

umin、umax——基本论域的最小值和最大值；

zmin、zmax——模糊论域最小值和最大值。

2.3 模糊RBF神经网络结构和算法

2.3.1网络结构

模糊RBF神经网络是四层结构，其结构如图4所示。

图4 模糊RBF神经网络结构

第一层为输入层。该层的节点与输入量直接相连，起着将输入量传送到下一层的作用[6]。第二层为模糊化层。这层的每个节点就代表了一个语言变量值(如PB、ZE)。它的作用是计算各输入分量属于各语言变量值模糊集合的隶属函数。隶属函数选用高斯型函数。第三层为模糊推理层。这层的每个节点对应一条模糊规则。它的作用是通过与模糊化层的连接完成模糊规则的匹配，计算每对模糊节点间的激活强度。第四层为输出层。输出结果为模糊推理层与各自权值的加权和。模糊神经网路控制器主要通过调整权值、隶属函数的中心值和宽度来实现控制。

2.3.2学习算法

模糊控制中每个输入分量的模糊分割数事先设定为7，输入分量的隶属函数采用高斯型函数。那么需要学习的参数主要是最后一层的连接权值wij和第二层的隶属函数中心值cij及其宽度σij。设性能指标函数为：

(2)

式中t(k)——期望输出；

y(k)——被控对象实际输出。

每一个迭代步骤k的控制误差为：

e(k)=t(k)-y(k)

(3)

进而可根据delta学习规则求得节点权值学习算法：

(4)

其中，η为学习速率，η>0；wj为第三层到第四层的权值(j=1,2…，N)。由增量式PID算法得：

u(k)=u(k-1)+Δu

Δu(k)=f4xc(j)

=f4(1)xc(1)+f4(2)xc(2)+f4(3)xc(3)

xc(1)=e(k)-e(k-1)

xc(2)=e(k)

xc(3)=e(k)-2e(k-1)+e(k-2)

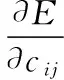
其中fi为第i层节点函数，xc为节点输入值。

考虑学习动量因子α的作用得节点权值、隶属函数中心和宽度的学习算法为：

wj(k)=wj(k-1)+Δwj(k)+α[wj(k-1)-wj(k-2)]

cij(k)=cij(k-1)+Δcij(k)+α[cij(k-1)-cij(k-2)]

σij(k)=σij(k-1)+Δσij(k)+α[σij(k-1)-σij(k-2)]

3 仿真实验

模糊神经网络控制器的仿真实验在Matlab软件的Simulink环境下进行。首先要确定仿真对象的数学模型，针对DMF回收精馏塔，采用实验建模法，拟合出主、副回路的简单传递函数模型为3/(180s+1)和0.2(36s+1)。进行阶跃响应实验，仿真模型如图5所示[7]。设定常规PID控制副调节器参数K=3，主调节器参数Kp=0.3、Ki=0.001、Kd=20；模糊神经网络控制器参数Kp=1.2、Ki=0.45、Kd=0.9，学习速率为0.21，动量因子α=0.019。量化因子初始设定为ke=50、kec=80，比例因子初始设定为ku=0.042。