基于多数据源的连铸软测量模型校正方法研究

张晓杰 纪振平

(沈阳理工大学信息科学与工程学院，沈阳 110159)

连铸是钢铁生产过程的核心环节，连铸传热模型可以实现铸坯的凝固状态和温度场分布的软测量，是进行连铸工艺优化和精确控制的基础，对提高连铸产品质量具有重要作用。而凝固传热模型的准确性是模型应用的前提[1]，其中决定模型准确性的边界条件中，二冷区各冷却段对流换热系数的确定是难点和关键[2]。

连铸机二冷区各冷却段对流传热系数主要由冷却水流量、铸坯表面温度及设备结构等因素决定[3～5]。但由于连铸机的设备参数各异，且生产钢种和喷嘴的型号不同，使得每台连铸机的模型边界条件各异，因此模型的边界条件必须结合连铸机的具体测量数据来确定。由于对实际连铸机各冷却段对流换热系数缺乏直接的检测手段，因此通常采用间接检测与之相关的物理量再通过反演计算的方法得到对流换热系数。这个反演计算过程可以转化成参数优化问题[3,4]。

笔者通过在二冷区内、外测量铸坯表面温度建立测量数据集进行传热模型参数修正(即传热逆模型求解)，由于凝固传热模型求解过程存在相变而得不到解析解，因此采用群智能优化算法求解。为确保模型的准确性，需结合凝固坯壳厚度的测量数据来验证模型的准确性。

1.1 凝固传热数学模型

将连铸过程中的对流换热等效为导热，凝固过程中的潜热释放过程等效为比热的增加。因沿拉坯方向热传导相对较小，故忽略该方向的传热。建立连铸坯二维传热模型[4]：

(1)

式中ceff——等效比热容，ceff=dH/dT，J/(kg·K)；

H——热焓；

keff——等效导热系数，W/(m·K)；

T——铸坯温度，℃；

ρ——钢液密度，kg/m3。

假设ρ、H、keff是温度和钢种成分的函数。模型的初始条件忽略中间包到弯月面的温降，即：

T(x,y,0)=Tc

(2)

式中Tc——中间包钢水温度。

结晶器边界条件为：

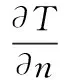
(3)

式中A、B——常数，通过测量结晶器进出口水温差计算得到；

t——铸坯自弯月面开始在结晶器中已经历的时间。

二冷区边界条件为：

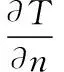
(Tair+273)4]

(4)

式中hi——二冷区第i冷却段换热系数，W/(m2·K)；

Twater——冷却水温度，℃；

Tair——环境空气温度，℃；

ε——辐射系数；

σ——斯蒂芬-波尔兹曼常数，W/(m2·K4)。

模型采用有限容积法进行离散化，并采用交差隐式算法进行求解。

1.2 传热系数

在凝固传热模型中，二冷区冷却段传热系数的确定是模型计算的关键和难点，根据喷淋方式的差异，二冷区各冷却段换热系数与水流密度的关系采用不同的经验公式确定。喷水冷却和气雾冷却时二冷区各冷却段换热系数的经验公式分别为[6]：

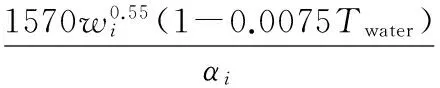
(5)

hi=1000wi/αi

(6)

式中wi——水流密度，L/(m2·s)；

αi——与设备有关的待辨识参数。

2 凝固传热模型校正

2.1 凝固传热模型校正方法

传热模型校正是基于二冷区冷却段的铸坯表面温度测量数据和模型计算数据的参数优化问题，其优化目标函数定义为：

(7)

式中Tmes,k、Tcal,k——铸坯表面温度测量值和根据传热模型得到的相应计算值；

m——测量数据值，其最优解作为模型参数辨识的结果。

模型校正过程就是不断调整αi使目标函数值最小的寻优过程。

2.2 优化算法

粒子群算法(Particle Swam Optimization，PSO)是由Eberhart R和Kennedy J于1995年提出的一种模拟鸟类捕食行为的全局优化算法[7]，具有步骤简洁、参数较少及易于实现等优点，被广发应用在多维连续空间优化问题等领域[8]。

PSO算法求解最优问题时，问题的解就是搜索空间中的一只鸟的位置，称这些鸟为“粒子”。所有的粒子都有一个被优化函数决定的适应值(候选解)和一个决定它们飞翔方向与距离的速度。PSO算法初始化为一群随机粒子(随机候选解)，然后通过迭代找到最优解。其中一个是粒子自身所找到的当前最优解，这个解称为个体极值pbest；另一个是整个群体当前找到的最优解，这个解称为全局极值gbest。PSO算法数学表示为：D维搜索空间中，有N个粒子，其中第i个粒子的位置是Xi=(xi1，xi2，…，xiD)，其速度为Vi=(vi1，vi2，…，viD)，其中，i=1，2，…，N。记第i个搜索到的最优位置为Pi=(pi1，pi2，…，piD)，也称pbest，整个粒子群搜索到的最优位置为Pg=(pg1，pg2，…，pgD)，也称gbest。粒子状态更新操作为：

vid(t+1)=w×vid(t)+c1r1×[pid-xid(t)]+c2r2[pgd-

xid(t)],i=1,2,…,N,d=1,2,…,D

(8)

xid(t+1)=xid(t)+vid(t+1)

(9)

vid∈[-vmax,vmax]

式中c1、c2——学习因子，是非负常数；

r1、r2——介于[0，1]之间的随机数；

t——当前迭代次数；

vmax——之前设定的最大速率(边界值)；

w——非负常数，称为惯性因子。

标准PSO存在容易早熟和陷入局部极值的缺点，为提高PSO的全局搜索能力，加快算法的收敛，笔者拟采用自适应粒子群算法(APSO)求解连铸传热逆模型[9]：

w(t+1)=4.0w(t)[1-w(t)],w(t)∈(0,1)

(10)

3 模型校正和结果分析

3.1 连铸机结构和工艺参数

研究对象为国内某大型钢厂方坯连铸机，其结构如图1所示。测试时生产钢种为HPB235，连铸机设备主要技术参数如下：

连铸机类型 连续矫直全弧形

流数 6流

弧形半径 10m

铸坯断面尺寸 160mm×160mm

结晶器长度 950mm

振动方式和曲线 全板簧、非正弦

二次冷却段结构 零段0.32m，水冷却；一段1.95m，二段5.69m，三段4.55m，气雾冷却测温时连铸机的工艺参数见表1。

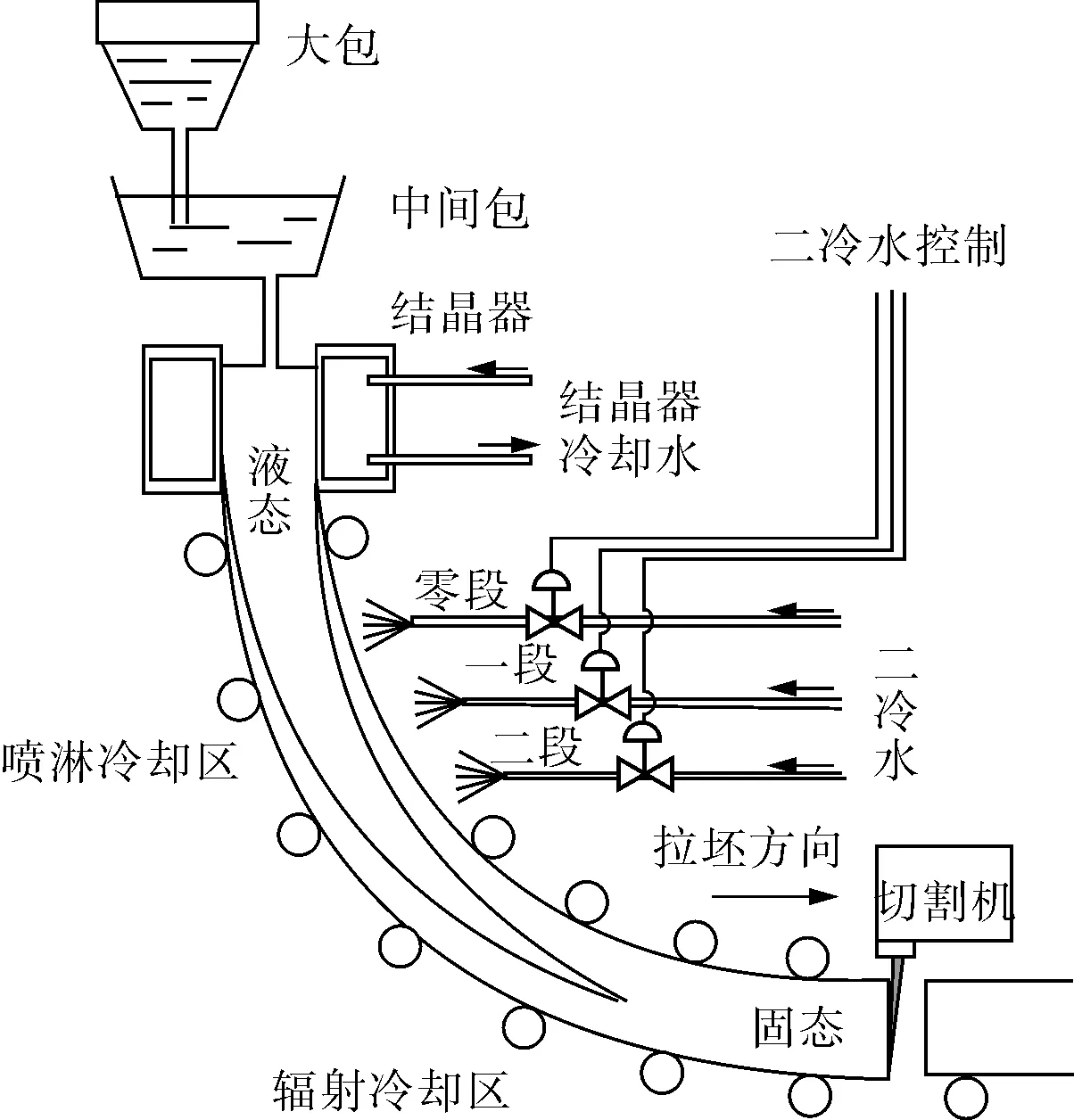
图1 连铸机结构示意图

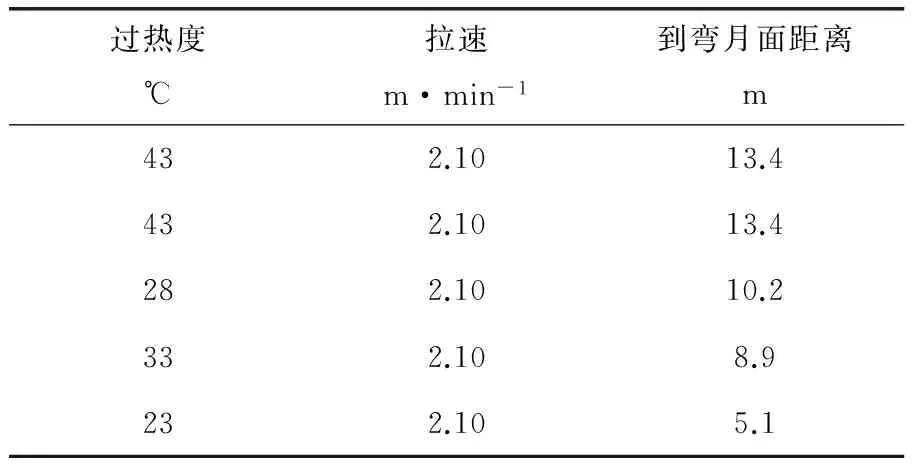
表1 测温时连铸机的工艺参数

3.2 铸坯表面温度测量

在二冷区内测温要考虑高温、水蒸气及氧化铁皮等因素的影响，因此测温时需对测温仪表、测量位置、测量时间和测量点数进行合理选择。笔者采用Mikron公司生产的比色测温仪M190在二冷区和出口5个测温点处进行铸坯表面测温。5个测温点300s时长的温度如图2所示。

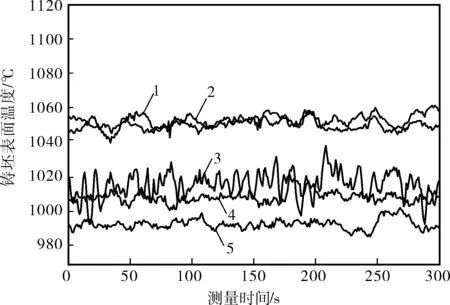
图2 铸坯表面温度测量曲线

3.3 模型校正结果分析

笔者采用APSO算法对模型参数进行参数辨识，算法选用参数有：ω=0.5，c1=c2=1.4962，最大迭代次数为100，粒子数Np=100，ai∈[0.1，10.0]，D=1、2、3、4。参数辨识结果为：a1=2.99，a2=1.76，a3=2.15，a4=2.08。

为验证模型计算的准确性，笔者选择在离弯月面8.8m处对铸坯进行射钉测量凝固坯壳厚度，射钉取样的硫印图如图3所示。

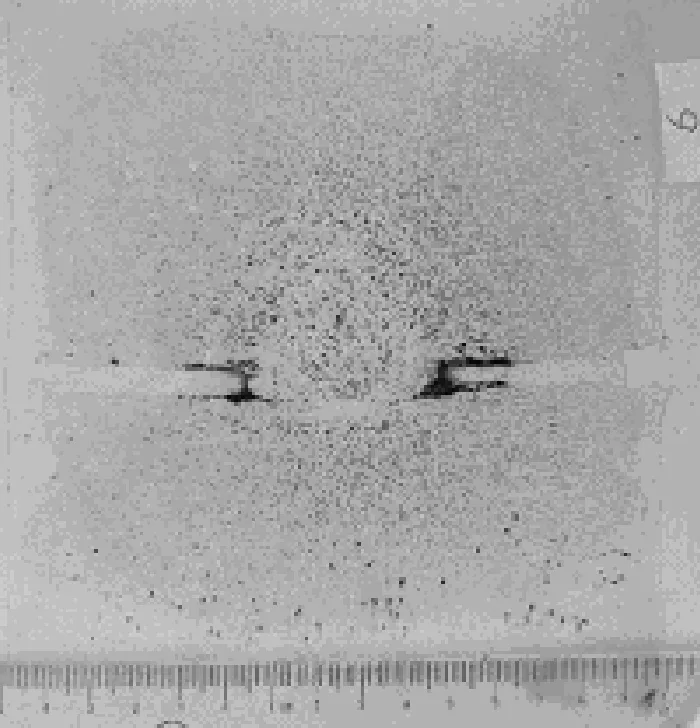
图3 射钉取样的硫印图

不同工况下的测量数据见表2。将测量结果与模型计算结果进行比较，从表2可以看出：校正后，模型的计算偏差小于2mm，满足工程应用要求。

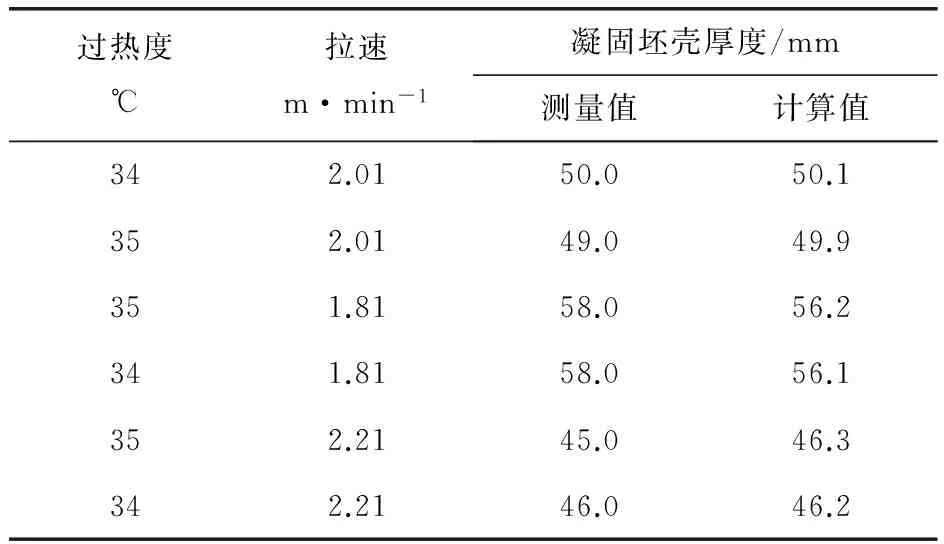
表2 射钉测量值与模型计算值的比较

图4为二冷区出口处测量的铸坯表面温度与校正后模型的计算温度的跟踪情况。从图4可以看出：校正后，模型的计算误差不大于±12℃，可用于实际连铸机的计算分析。

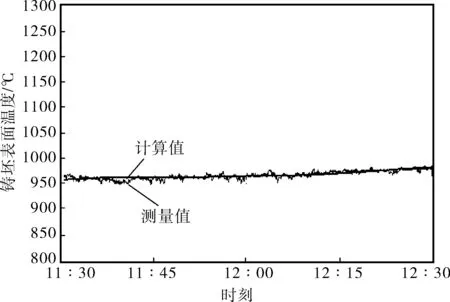
图4 铸坯表面温度测量值与计算值的对比

4 结束语

在铸坯不同位置测量其表面温度，根据测量数据和传热模型的计算数据，采用自适应粒子群优化算法对二冷区各冷却段对流传热系数进行辨识，并以此传热系数作为边界条件模拟铸坯凝固过程，结果表明：采用APSO算法进行连铸传热模型校正问题的优化求解，算法简单、收敛速度快，具有较好的全局寻优能力；采用校正后的模型对连铸传热过程进行在线计算，温度和坯壳厚度的计算值与测量值偏差满足工程应用要求，验证了基于多数据源的模型校正方法的准确性，提高了模型的可靠性。

[1] Spitzer K H, Harste K, Weber B, et al. Mathematical Model for Thermal Tracking and On-line Control in Continuous Casting[J]. ISIJ International, 1992, 32(7): 848～856.

[2] Brimacombe J K. The Challenge of Quality in Continuous Casting Processes[J]. Metallurgical and Materials Transactions B, 1999, 30(4): 553～566.

[3] Stota D.Reconstruction of the Heat Transfer Coefficient on the Grounds of Experimental Data[J]. Journal of Achievements in Materials and Manufacturing Engineering, 2009, 34(1):63～70.

[4] 阳剑，孟红记，纪振平，等. 基于混沌粒子群算法的连铸传热模型参数辨识[J]. 东北大学学报(自然科学版)，2014，35(5)：613～616.

[5] 巫英伟，卢义，索晓娜，等. 板坯连铸二冷区表面传热系数的预测方法[J]. 西安交通大学学报，2006，40(1)：26～30.

[6] Louhenkilpi S, Laitinen E, Nieminen R. Real-time Simulation of Heat Transfer in Continuous Casting[J]. Metallurgical Transactions B, 1993, 24(4): 685～693.

[7] Eberhart R，Kennedy J. A New Optimizer Using Particle Swarm Theory[C].Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Nogoy:IEEE,1995: 39～43．

[8] 孟红记，郑鹏，武荣阳，等. 基于改进PSO算法的连铸二冷过程优化仿真[J]. 系统仿真学报，2006，18(4)：866～869.

[9] Jiang C W, Bompard E. A Hybrid Method of Chaotic particle Swarm Optimization and Linear Interior for Reactive Power Optimisation[J]. Mathematics and Computers in Simulation, 2005, 68 (1/3) : 57～65.