多样性分布参数的粒子群算法及其在过程动态优化中的应用

王应虎 范勤勤 颜学峰

(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)

粒子群优化(PSO)算法是Kennedy J和Eberhart R在1995年通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的启发式算法[1]。PSO算法有较快的收敛速度且对非线性、多峰问题具有较强的全局搜索能力，在PID控制器优化及系统辨识等领域得到了广泛的应用[2～4]。为了提高PSO算法的稳定性并避免早熟收敛，文献[5]通过一个模糊惯性权重和模糊控制器实现速度和位置的更新；文献[6]通过K均值分类技术将种群分为3个簇，根据簇中最优和最差粒子的变化实现加速因子自适应；文献[7]基于相对距离提出了一种自适应参数改进算法，使个体在进化中有不同的惯性权重和社会因子。相关的研究工作均表明：通过算法参数的自适应，可以有效提高PSO算法的寻优性能。但何种自适应策略是算法参数最佳自适应策略仍是一个广泛研究的问题。

笔者针对PSO算法参数自适应策略进行研究，提出一种多样性分布参数的粒子群算法(DDPPSO)。该算法在初始化时增加了参数种群，即每个粒子在迭代中拥有自己的控制参数，由当前适应度值确定每个粒子的参数权重，进而计算下一代的控制参数均值，通过控制参数均值与自适应方差的正态分布来产生下一代控制参数，控制参数呈现多样性分布，使粒子群体与参数群体通过交互协同进化，优秀的参数个体能使粒子获得良好的进化，粒子的进化性能又作为参数个体多样性分布的评价，进而为优化算法提供实时的最佳参数，提高算法的搜索性能。假设优化函数为求最小值问题，粒子xi的参数种群为ωiG、c1iG、c2iG，DDPPSO算法的步骤为：

a. 随机生成粒子种群和参数种群，种群规模为NP，最大进化代数为Gm，当前进化代数G=0；

b. 计算个体适应度值f(xiG),令个体最优值pbestiG=xiG，最小适应度值个体作为种群最优值gbestG；

c. 更新粒子速度和位置；

d. 计算最大适应度值和参数权重；

e. 计算参数的加权平均值；

f. 计算参数的自适应方差；

g. 参数加权平均值与自适应方差通过正态分布产生下一代参数群体，并随机一对一地分配给粒子种群；

h. 更新局部最优和全局最优；

i. 重复步骤c～h的操作，直到进化代数超过最大进化代数或已找到全局极值。

更新粒子速度和位置的公式为；

viG+1=viG×ω+c1×rand1×(pbesti-xiG)+

c2×rand2×(gbest-xiG)

(1)

xiG+1=xiG+viG+1

(2)

计算最大适应度值和参数权重公式为：

计算参数的加权平均值公式为：

计算参数自适应方差的公式为：

2 参数选取

为了实现多样性分布参数的粒子群算法，对参数的选取进行了多次实验，主要是参数种群中各个参数初始化的范围和自适应方差的计算公式。在实验中，种群大小为40、30维，最大迭代次数为1 000，算法独立运行20次的均值和方差作为比较结果(表1)，其中参数1、2、3分别表示惯性权重、认知因子和社会因子。

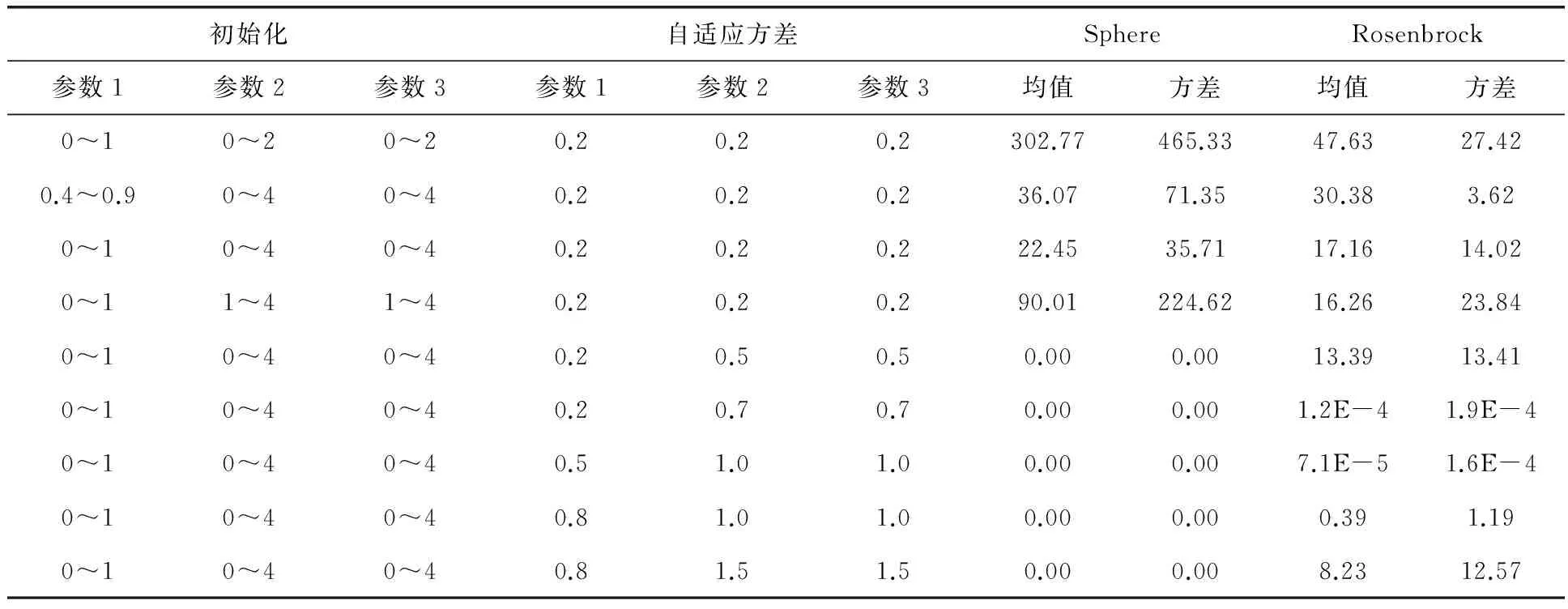
表1 参数选取实验结果

由实验结果可以看出，在参数初始化中，惯性权重为0～1的均匀分布，认知因子、社会因子为0～4的均匀分布时，方差和均值均最优；在自适应方差中，惯性权重在0.2～0.5之间变化，认知因子、社会因子在0.7～1.0之间变化时结果较好。

3 实验结果及分析

3.1 实验

为了检验DDPPSO算法的全局搜索能力，将DDPPSO算法与4种新改进的粒子群算法进行比较。这4种算法分别是：文献[8]提出的邻域搜索多样性增强的粒子群算法(DNSPSO)、文献[9]提出的全面学习粒子群算法(CLPSO)、文献[10]提出的自适应粒子群算法(APSO)和文献[11]中基于相反学习的粒子群算法(GOPSO)。算法的参数设置如下：种群大小统一为40，维数为30时目标函数评价次数为200 000，维数为100时目标函数评价次数为500 000。为排除随机性，实验以30次独立实验的统计结果进行分析，各种算法的其他参数设置可参考其文献。实验系统基于Intel Core(TM)2 Duo CPU E7500@2.93GHz，2.00GB，Windows7，MATLAB R2010b环境。

3.2 结果分析

表2列出了DDPPSO与对比的4种算法对15个标准测试函数独立运行30次的均值和方差，除了DDPPSO之外，其他各种算法的结果均来自于文献[8]。在用于比较的各种算法中，CLPSO和APSO算法在15个测试函数中均未找到最优解，其优化性能较差；GOPSO算法在6个测试函数中找到极值，其寻优性能和优化精度较好；DNSPSO算法在15个测试函数中，有8个测试函数能找到全局极值，3个测试函数搜索结果较好，在寻优精度和稳定性方面有更好的性能；但DDPPSO算法有10个测试函数找到全局极值，有13个测试函数的均值和方差较其他4种算法表现更优，特别在Rosenbrock函数的寻优上有着非常优秀的表现，有两个测试函数的结果相比文献最优值较接近。从总体而言，DDPPSO算法比其他4种改进算法在全局搜索和稳定性方面有更强的优势。

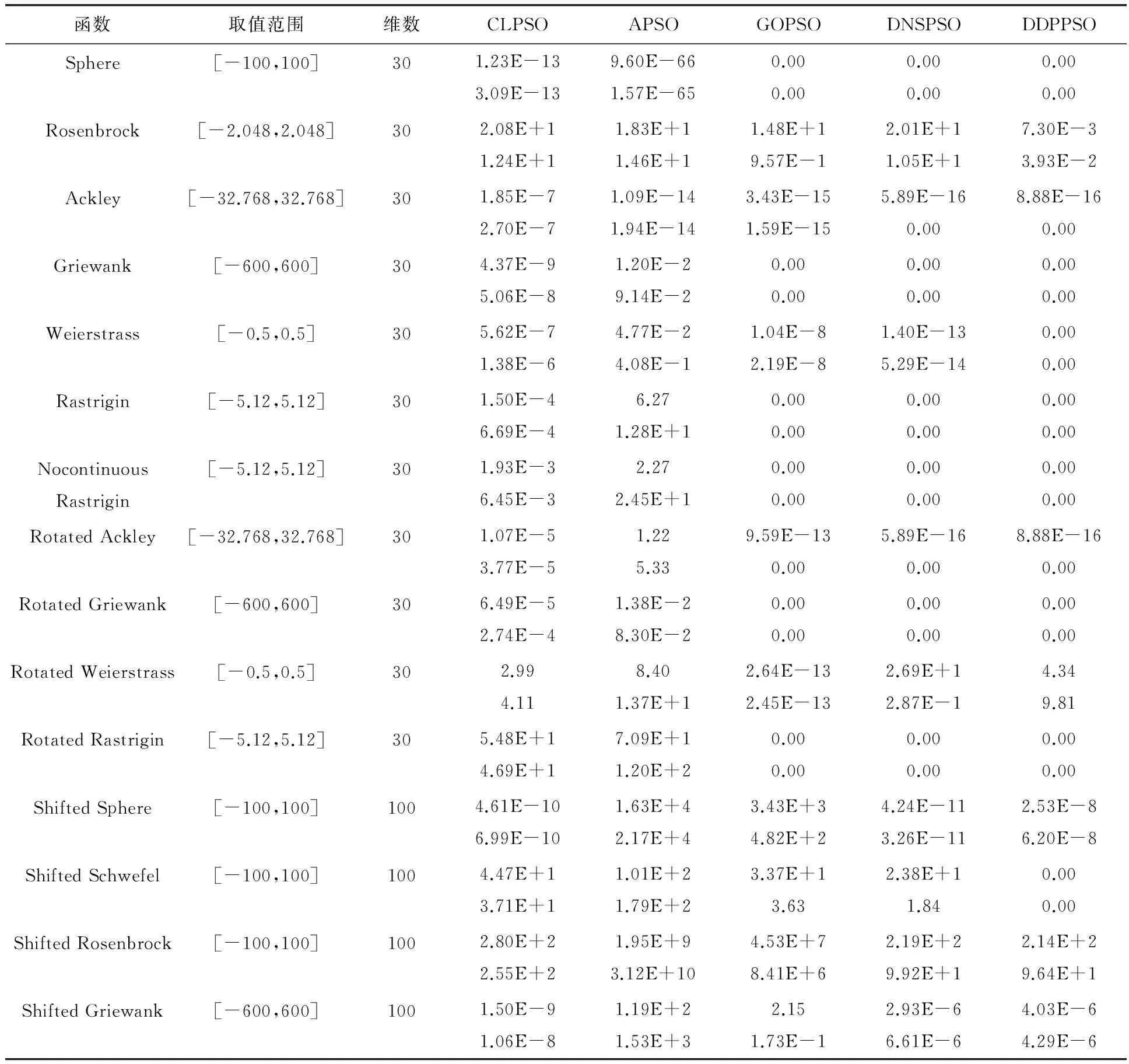
表2 测试函数运行30次的均值和方差

4 DDPPSO算法应用于生物反应器动态优化

4.1 Park-Ramirez生物反应器模型

Park和Ramirez提出了生物反应器的优化模型，其物理意义为：生物反应器中酵母菌在生产内源蛋白质时，通过流加的方式为菌体新陈代谢提供补料，过程优化数学模型如下[12]：

maxJ=x1(tf)x5(tf)

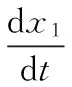
4.2 Park-Ramirez生物反应器优化结果

使用Runge-Kutta法求解微分方程，计算出J来进行比较，算法独立运行10次的比较结果见表3。

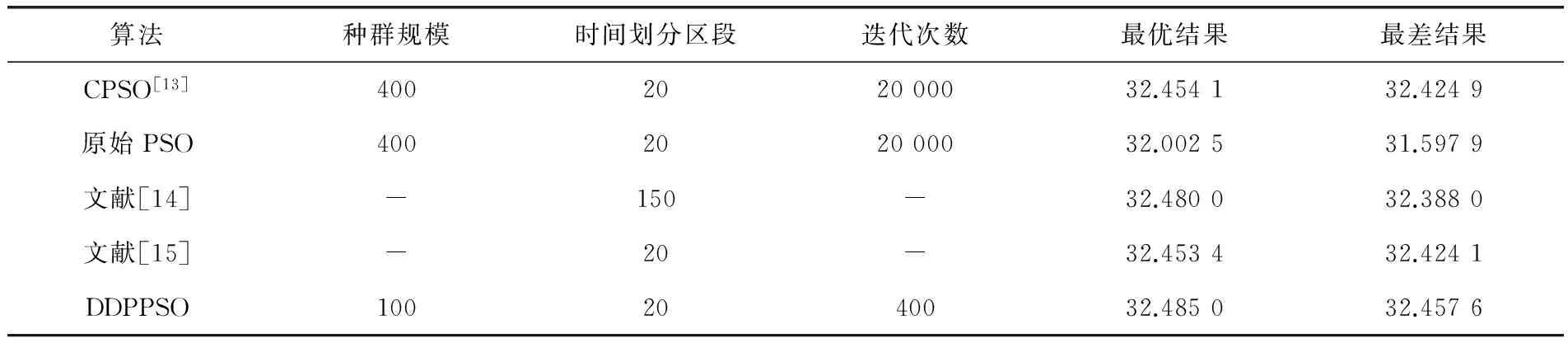
表3 动态优化结果对比

文献[14]采用Restricted second-order information法进行求解，因时间划分越多控制操作越复杂，考虑实际问题，笔者只对区间进行20等分，文献[14]未记载种群大小和迭代次数。从表4的实验结果可以看出，在种群规模和迭代次数明显减少的情况下，DDPPSO所得优化结果较文献[13～15]有较大改进。可见，利用DDPPSO求解生物反应器的动态优化问题是有效的，解的精度较高而且比较稳定。

5 结束语

基于多样性分布参数的粒子群算法通过迭代过程中适应度值的变化更新参数权重，在实现在粒子进化寻优的同时，惯性权重和加速因子能实现自适应进化。15个测试函数的仿真研究表明，DDPPSO算法能保证算法的全局寻优性能与局部搜索能力，提高算法的收敛速度和解的精度。最后，将DDPPSO算法应用于生物反应器的动态优化，其结果较文献报道的数据有较大的提高。

[1] Kennedy J,Eberhart R.Particle Swarm Optimization[C].IEEE International Conference on Neural Networks,IV.Piscataway,NJ:IEEE,1995:1942～1948.

[2] 应明峰,鞠全勇,高峰.基于粒子群优化的PID控制器设计与应用[J].计算机仿真,2012,28(11):283～287.

[3] 黄宇,韩璞,刘长良，等.改进量子粒子群算法及其在系统辨识中的应用[J].中国电机工程学报,2011,31(20):114～120.

[4] 严巳杰，胡建华，黄炳琼，等.基于粒子群优化算法的板翅式换热器优化设计[J].化工机械，2012,39(1):55～57.

[5] Liu C X,Ouyang C J.An Adaptive Fuzzy Weight PSO Algorithm[C].International Conference on Genetic and Evolutionary Computing.Shenzhen:ICGEC,2010:8～10.

[6] Bao G Q, Mao K F. Particle Swarm Optimization Algorithm with Asymmetric Time Varying Acceleration Coefficients[C]. International Conference on Robotics and Biomimetics.Gulin:ROBIO,2009:2134～2139.

[7] Li G,Xu C.A Novel Particle Swarm Optimization Based on the Self-Adaptation Strategy of Acceleration Coefficients[C]. International Conference on Computational Intelligence and Security.Beijing:Computational Intelligence and Security,2009:277～281.

[8] Wang H,Sun H,Li C G,et al.Diversity Enhanced Particle Swarm Optimization with Neighborhood Search[J].Information Sciences,223:119～135.

[9] Liang J J,Qin A K,Suganthan P N. Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Multimodal Functions[J]. IEEE Transactions on Evolutionary Computation,2006,10(3):281～295.

[10] Zhan Z H,Zhang J,Li Y,et al.Adaptive Particle Swarm Optimization[J].IEEE Transactions on Man and Cybernetics,2009,39(6):1362～1381.

[11] Wang H,Wu Z J,Rahnamayan S,et al.Enhancing Particle Swarm Optimization Using Generalized Opposition-based Learning[J]. Information Sciences,2011,181(20):4699～4714.

[12] 林可鸿,贺益君,陈德钊.混合优化人工免疫网络用于过程动态优化[J].浙江大学学报(工学版),2008,42(12):2181～2186.

[13] 莫愿斌,陈德钊,胡上序.混沌粒子群算法及其在生化过程动态优化中的应用[J].化工学报,2006,57(9):2123～2127.

[14] Balsa-Canto E,Banga J R,Alonso A A, et al.Dynamic Optimization of Chemical and Biochemical Processes Using Restricted Second-order Information[J]. Computers & Chemical Engineering,2001,25(4):539～546.

[15] 刘贺同,莫愿斌.粒子群复形法求解生物反应器的补料优化[J].机床与液压,2007,35(5):94～97.