基于多工况混合模型的故障监控方法研究

高俊峰 周凌柯

(南京理工大学自动化学院，南京 210094)

近年来，以PCA为代表的多元统计过程性能监控和故障诊断技术在化工过程中得到了成功应用[1，2]。但此类方法假定过程变量服从正态分布，且来自单一的稳定工况。对于多工况过程，目前的监测方法大多采用多模型方法[3～6]。Hwang D H和Han C H提出了一种基于多层聚类的超级PCA模型来解决多工况下化工过程的实时监测问题[3]。Lane S等提出一种通用子空间模型来监控多工况半间歇过程[4]。Zhao S J等为多工况过程监测开发了多PCA/PLS模型[5,6]。这些方法的共同点是通过聚类或经验来划分工况，工况数的选择和工况界定较多地依赖于过程知识。为减轻监测方法对过程知识的依赖，近年来高斯混合模型(Gaussian Mixture Model，GMM)被应用到多工况过程监测中来。GMM的参数一般使用EM(Expectation Maximization)算法迭代估计，然而常规EM算法必须事先给定混合模型的分量数目，且在参数估计过程中不能自动调整。但在实际工业过程中，过程工况数经常是无法预知的，因此，近几年许多学者采用的方法是针对不同的分量数目多次运行EM算法，计算量较大。Ma J等指出未知分量数目的高斯混合模型建模问题等价于最大化贝叶斯阴阳协调函数，并从理论上分析和证明了BYY协调函数用于选取高斯分量数目的有效性[7]。

为了解决多工况故障监控中存在的问题，笔者建立了一个多工况混合模型。该模型首先采用常规EM算法估计各工况的GMM参数，然后采用BYY算法根据所估计出的GMM参数来判断工况数。迭代进行上述过程，直到GMM参数和工况数都收敛为止。混合模型建立后，通过在其每个分量中建立PCA模型，建立了一个多工况故障监控模型。该监控模型通过贝叶斯方法对被监控样本实施自动工况划分。

1.1 EM算法

假设x∈Rm是一个取自多工况过程的m维样本，那么其在有限GMM下的概率密度函数可表示为：

(1)

其中K是包含在GMM中高斯分量的个数。将混合模型所有的参数合并到向量Θ={α1,m1,Σ1,…,αK,mK,ΣK}，其中mi、Σi代表第i个高斯分量的均值向量和协方差矩阵，αi表示其在混合模型中的权重。混合概率p(x|Θ)本质上是所有高斯分量的加权概率和。权重αi可以理解为任意样本数据来自于第i个高斯分量的先验概率。各高斯分量的概率密度方程可以表示为：

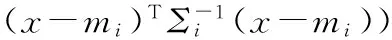
(2)

假定Θ中的模型参数都是常量且没有任何的先验知识，那么给定样本数据集X={x1,x2,…,xN}，混合模型参数Θ通常可通过最大化似然方程L(Θ)求出：

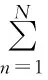
(3)

然而，当事先并不知道X中样本数据所属的高斯分量时，式(3)所定义的方法就会失效，而EM算法则可以通过迭代估计的方法解决上述混合模型参数估计问题[8]。

给定混合高斯分量数K和Θ的初值Θ0，EM算法通过不断重复E-step和M-step迭代估计Θ，直至Θ单调收敛到其最优估计值。

E-step，给定Θ(t)，计算完全数据下的log似然函数的期望：

(4)

M-step，通过最大化似然函数Q(Θ|Θ(t))求取Θ(t+1)：

(5)

1.2 BYY算法

如上所述，在用EM算法迭代估计混合模型参数Θ时，必须事先给定混合模型的高斯分量数K。然而，在没有任何先验知识的情况下，K很难被准确地给出。为了解决这个问题，笔者在EM收敛之后，采用BYY算法估计工况数[7]。若所估计的工况数收敛，则混合模型参数估计停止。否则，以采用BYY算法估计出的混合工况数为条件重新执行EM算法。估计混合工况数的BYY协调函数定义如下：

(6)

1.3 基于MPMM的多工况过程监控模型

在用MPMM建立起GMM后，混合高斯分量数即为工况数，各个高斯分量对应各个稳定工况的分布特性。为了在所建立GMM的基础上引入PCA算法，建立多工况过程监测模型，需要对训练样本数据进行工况划分。对于训练样本数据xn，其所属工况为：

(7)

所有训练样本数据工况划分结束后，与传统PCA相似，对于每一监控样本x，定义两个监控统计量T2和SPE：

T2=xPΛkPTxT

SPE=‖(I-PPT)x‖2

(8)

(9)

其中，k是主元个数，N是训练样本数。g和h的计算式为：

hg=mean(SPE)

2g2h=var(SPE)

(10)

过程监测时，需要为每个新监测样本xn找到其所属工况。笔者把xn属于各个高斯分量的后验概率作为相应的隶属度。计算方法为：

(11)

2 仿真研究

TE过程是由Downs J J和Vogel E F于1993年提出的一个实验平台，它被广泛应用于评估和比较过程监测方法的有效性[9]。其流程如图1所示[10]，该过程有12个操作变量和41个测量变量。在41个测量变量中，前22个是连续变量，另外19个是离散变量。本节选取16个连续变量用于过程故障监测。

图1 TE过程流程

在建立MPMM时，让TE过程仿真运行70h，采样间隔为0.01h，产生一个由两个稳定工况构成的训练样本数据集。这两个稳定工况是在仿真过程中改变TE过程的反应器压力和反应器液位水平得到的。在仿真开始时，反应器压力和液位水平为其初始值(2 800kPa和65%)，此时TE过程处于工况1；在仿真进行到10.033h时，降低反应器压力至2 705kPa，液位水平保持不变，TE过程进入工况2。取各稳定工况1 000个数据点，构成一个由2 000个数据点组成的训练样本数据集，然后采用MPMM对此训练样本数据集建模，所建模型中各高斯分量在混合模型中所占比重分别为0.508 3和0.491 7，与实际值一致。因此，所建模型很好地描述了3个工况下训练样本数据的分布特性。

为了验证MPMM监控复杂工业过程的有效性，笔者将其分别对正常和阶跃扰动两种工业过程进行监测。正常过程测试样本数据集由3个工况正常运行条件下的采样数据构成，每个工况300个样本点。阶跃扰动测试样本数据集通过向工况1中引入阶跃变化的故障2产生。故障引入的位置在第100个样本点处，共有1 000个样本点。故障2通过改变组分B的含量产生。

图2 正常数据集的仿真结果

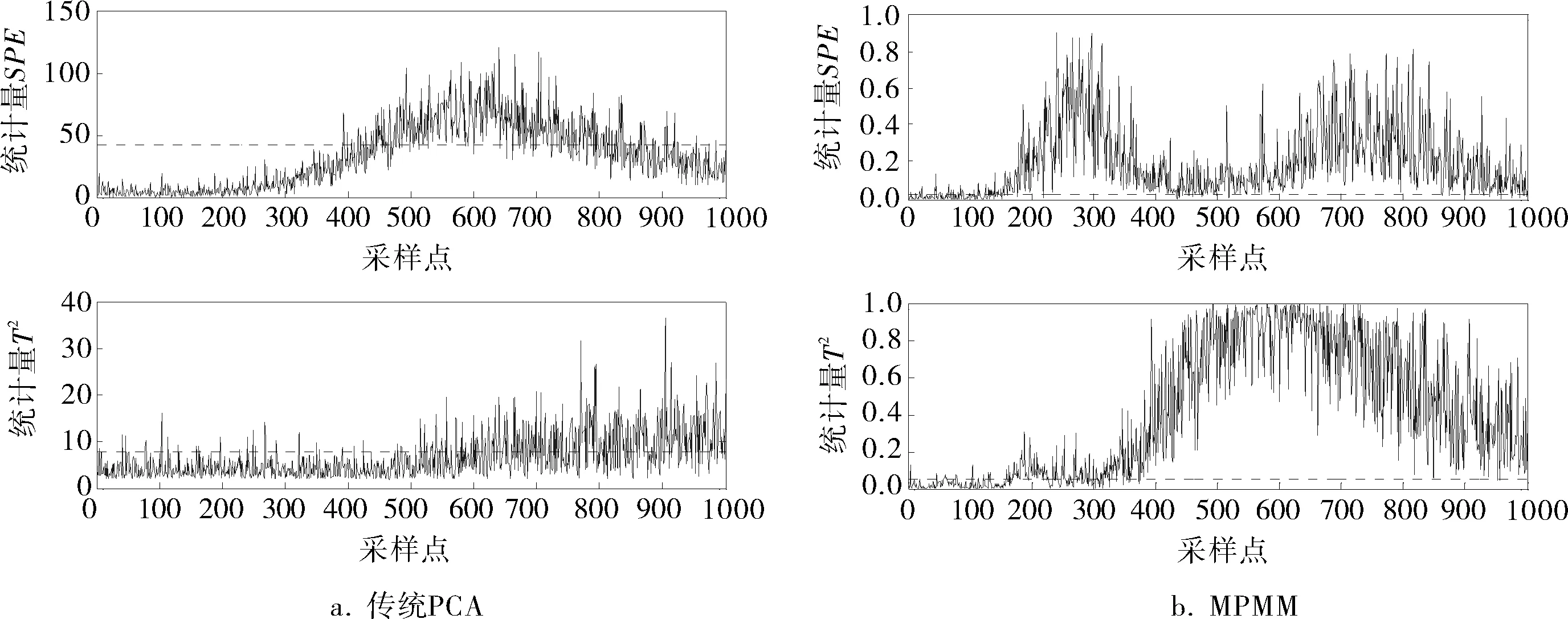
图3 阶跃扰动故障2监控结果

图2、3所示仿真结果表明，笔者所提方法MPMM的多工况过程监控性能远优于传统PCA，而且监控延时较小。说明MPMM可以有效且准确地监控多工况工业过程。

3 结束语

基于BYY算法和PCA数据降维技术，建立了一个多工况混合模型。该模型克服了采用常规EM算法建立混合模型时必须事先给出混合工况数的限制，极大地提高了模型的适用范围。模型建立后，通过在混合模型每个分量中构建PCA模型，建立了一个多工况故障监控模型。最后的仿真研究证明了MPMM在多工况过程监测中的有效性。

[1] Chiang L H，Ressell E L，Braatz R D. Fault Detection and Diagnosis in Industrial System[M].London：Springer-Verlag，2001：198～205.

[2] Choi S W，Martin E B，Morris A J.Fault Detection Based on a Maximum-Likelihood Principal Component Analysis (PCA)Mixture[J].Industrial and Engineering Chemistry Research，2005，44：2316～2327.

[3] Hwang D H，Han C H.Real-time Monitoring for a Process with Multiple Operating Modes[J].Control Engineering Practice，1999，7(7)：891～902.

[4] Lane S，Martin E B，Kooijmans R，et al.Performance Monitoring of a Multi-product Semi-batch Process[J].Journal of Process Control，2001，11(1)：1～11.

[5] Zhao S J，Zhang J，Xu Y M.Monitoring of Processes with Multiple Operating Modes Through Multiple Principal Component Analysis Models[J]. Industrial and Engineering Chemistry Research，2004，43(2)：7025～7035.

[6] Zhao S J，Zhang J，Xu Y M.Performance Monitoring of Processes with Multiple Operating Modes through Multiple PLS Models[J].Journal of Process Control，2006，16(7)：763～772.

[7] Ma J，Wang T，Xu L.A Gradient BYY Harmony Learning Rule on Gaussian Mixture with Automated Model Selection[J].Neurocomputin，2004，56：481～487.

[8] Dempster A P，Laird N M，Rubin D B.Maximum-likelihood from Incomplete Data via the EM Algorithm[J].Journal of the Royal Statistical Society， Series B(Methodological)，1977，39(1)：1～38.

[9] Downs J J，Vogel E F.A Plant-wide Industrial Process Control Problem[J].Computers Chemisty Engineering，1993，17(3)：245～255.

[10] Lawrence R N.Decentralized Control of the Tennessee Eastman Challenge Process[J].Journal of Process Control，1996，6(4)：205～221.