基于出口压力脉动奇异值的离心泵早期汽蚀故障诊断

周云龙 吕远征

(东北电力大学 a.能源与动力工程学院；b.自动化工程学院，吉林 吉林 132012)

汽蚀故障的形成与发展改变了离心泵的正常流场，不但影响其性能，还会造成异常振动和噪声，若气泡靠近过流部件溃灭，会对水泵零部件造成极大的损伤[1，2]。显然，及时诊断出离心泵的早期汽蚀故障可大幅降低损失，延长其使用寿命。

一般认为，在流量恒定的情况下扬程下降3%时的有效汽蚀余量NPSHa为必须汽蚀余量NPSHr。但采用这种典型的能量法诊断出离心泵发生汽蚀时，实际的汽蚀区域已经发展到了一定程度，部分过流部件已经受到损伤[3]，因此不适用于在线监测系统。在工业生产中经常使用振动信号监测诊断方法，其通用性较好，可检测的故障种类也很丰富[4]，但是振动来源十分复杂，在监测早期汽蚀的微弱信号时不可靠，容易造成诊断迟滞。近年发展起来的超声波法[5]可以较好地诊断早期汽蚀，通过接收微小气泡溃灭时产生的超声波判断是否发生汽蚀，检测准确及时，但是配套检测设备成本高昂。随着计算流体力学理论的发展与测试方法的不断进步，对泵内流场与压力脉动的研究也在继续深入，文献[6]指出，汽蚀故障引起的流场变化与压力脉动信号有密切的相关性。周云龙和梁超用实验方法分析了汽蚀故障与入口压力脉动间的联系，验证了根据压力脉动信号进行早期汽蚀故障诊断的可行性[7]。而刘阳等指出，出口压力脉动比入口压力脉动包含的流场信息详尽[8]。

笔者利用出口压力脉动对早期汽蚀信号进行诊断。首先采用提升db4小波将离心泵出口压力脉动信号分解到不同的时频子空间，并将所有子空间的小波分解系数构造为时频信息矩阵，然后对矩阵进行奇异值分解以提取特征向量，最后借助LM(Levenberg-Marquardt)算法的人工神经网络(ANN)建立特征样本到汽蚀各阶段的映射。此方案充分发挥提升小波优秀的时频分辨特性、易于重构和计算迅速的特点[9]，利用信号奇异值唯一性的优点提取可靠且敏感的故障特征量[10]，同时借助人工神经网络良好的非线性输入输出和联想功能完成故障诊断，使其在准确度、速度和泛化性能上达到工业应用的要求。

1.1 压力脉动信号分析

离心泵用于在某一恒定流量下产生固定压差来运送介质，但实际压差并不稳定，在一个值附近波动，这种动态压力分量就是压力脉动。压力脉动的周期脉动与离心泵内部流场的变化有着密切关系，汽蚀故障下的流场与正常工况流场并不相同，这些区别也会在压力脉动信号体现。以ISWB65-160型卧式离心泵在NPSHa为10.8、1.8m工况下的压力脉动信号为例，采样频率2 048Hz，采样时间500ms，其时域信号如图1所示。

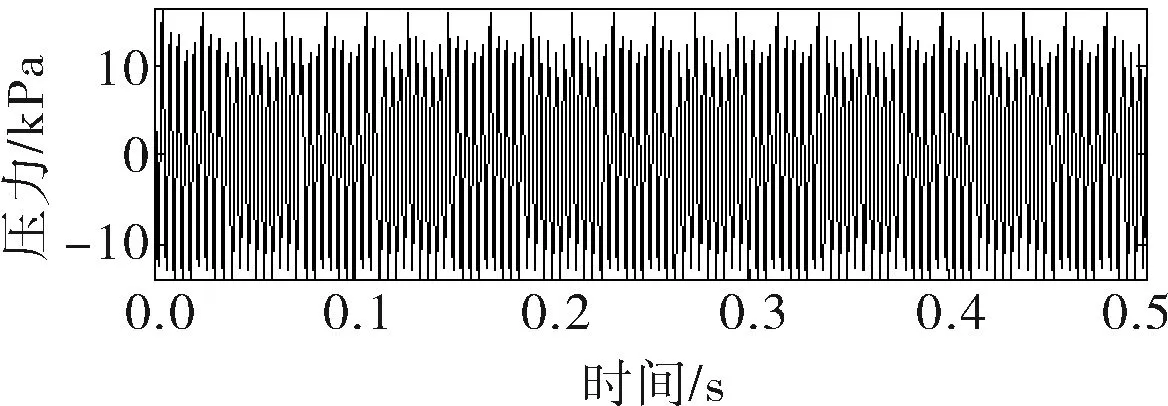
a. NPSHa=10.8m

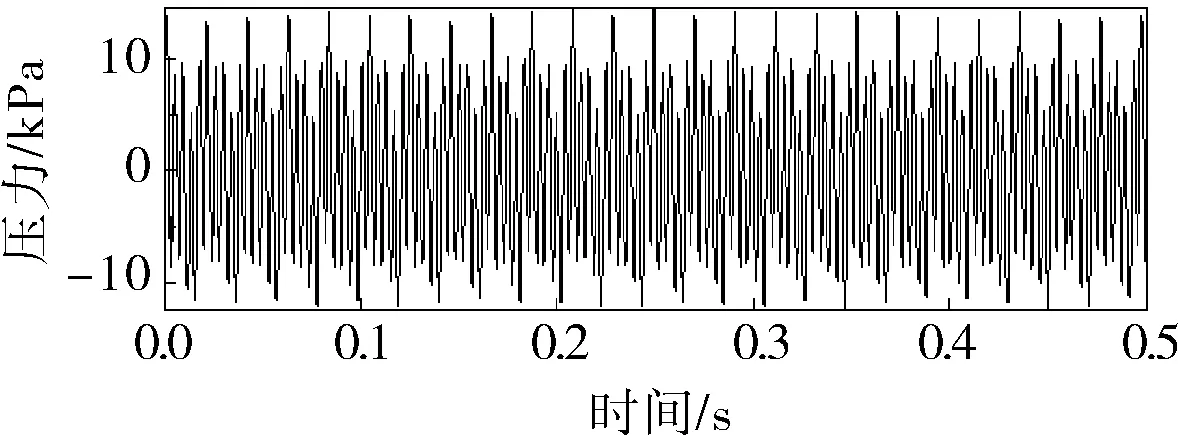
b. NPSHa=1.8m

显然，两种工况下的压力脉动时域信号存在较大区别，二者的时频功率谱如图2所示，两种工况下压力脉动信号均以低频分量为主，大多集中在0～500Hz，整体频段均充斥着随机噪声。正常工况下频率成分清晰，平均幅值也较低，而发生汽蚀故障后，信号的频率成分开始变得复杂，低频模态增加，平均幅值也大幅提高，并且具有非线性、非平稳特征，经典的时频分析法已无法迅速提供高分辨率的特征信息。

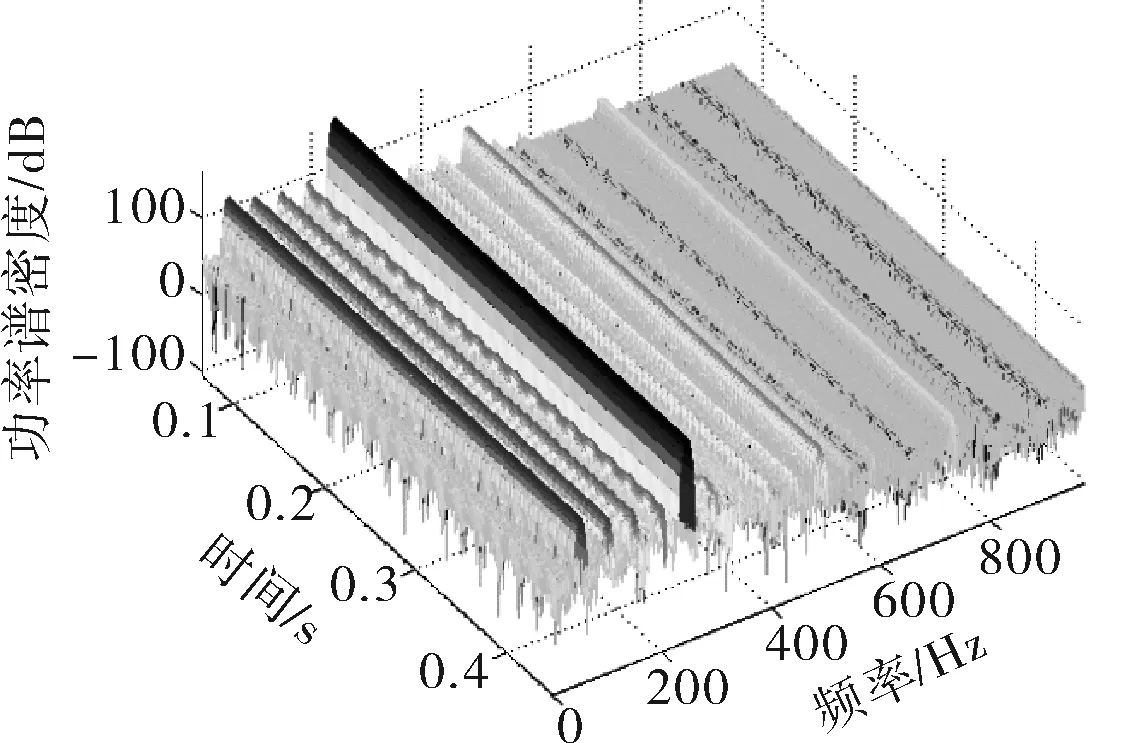
a. NPSHa=10.8m

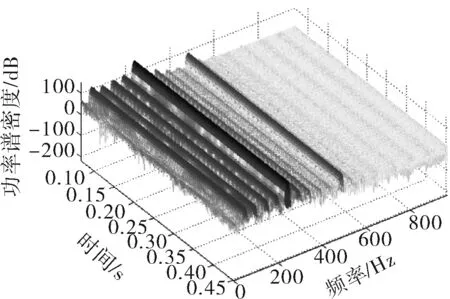
b. NPSHa=1.8m

1.2 提升小波分解

为了更迅速准确地从压力脉动信号中提取汽蚀特征信息，笔者采用了适合处理非平稳、非线性问题的数学方法，即提升小波理论[11]。提升小波分解算法主要由3部分构成：

a. 分裂。将长度N=2j的原信号Sj(t)分解成奇数样本序列oj和偶数样本序列ej。

b. 对偶提升。用ej预测oj，其预测误差为细节信号，有Dj+1=oj-K(ej)其中K(·)为预测器，此过程可逆，如果预测器确定，可根据Dj+1与ej完全重构原信号Sj(t)。

c. 提升。根据Dj+1修正ej，得到的Sj+1拥有Sj(t)整体性质中的部分，可视为对原信号的平滑处理，且只包含Sj(t)的低频成分。修正过程为Sj+1=ej+U(Dj+1)，其中U(·)为更新器，此过程同样可逆，若U(·)确定，根据Sj+1和Dj+1完全可以重构提升前的ej。

根据文献[12]，db4在频谱泄漏和分辨率方面具有一定的优越性，在此利用db4小波的提升分别对NPSHa为10.8、1.8m两种工况下的离心泵出口压力脉动信号进行四层分解，近似信号与细节信号如图3所示，a4为低频近似信号，b4、b3、b2和b1为高频细节信号。

显然，原始信息被提升小波成功地分解到不同的子时频空间中，频段能量分配也较为合理，并且具有以下特点：

a. 提升小波完全不依赖傅立叶变换，在保留经典小波良好的时频分辨能力的基础上，可进行原位计算，并且有效减少了运算量，降低了所需储存空间，这一点非常适用于复杂工业诊断。

b. 利用提升算法，经典小波均可找到相应的提升格式，提升后对信号分解采用非抽样模式，其小波系数矩阵会保留完备的时域信息和更详细的频域局部化信息，这一优点将为信号的特征提取打下良好的基础。

a. NPSHa=10.8m

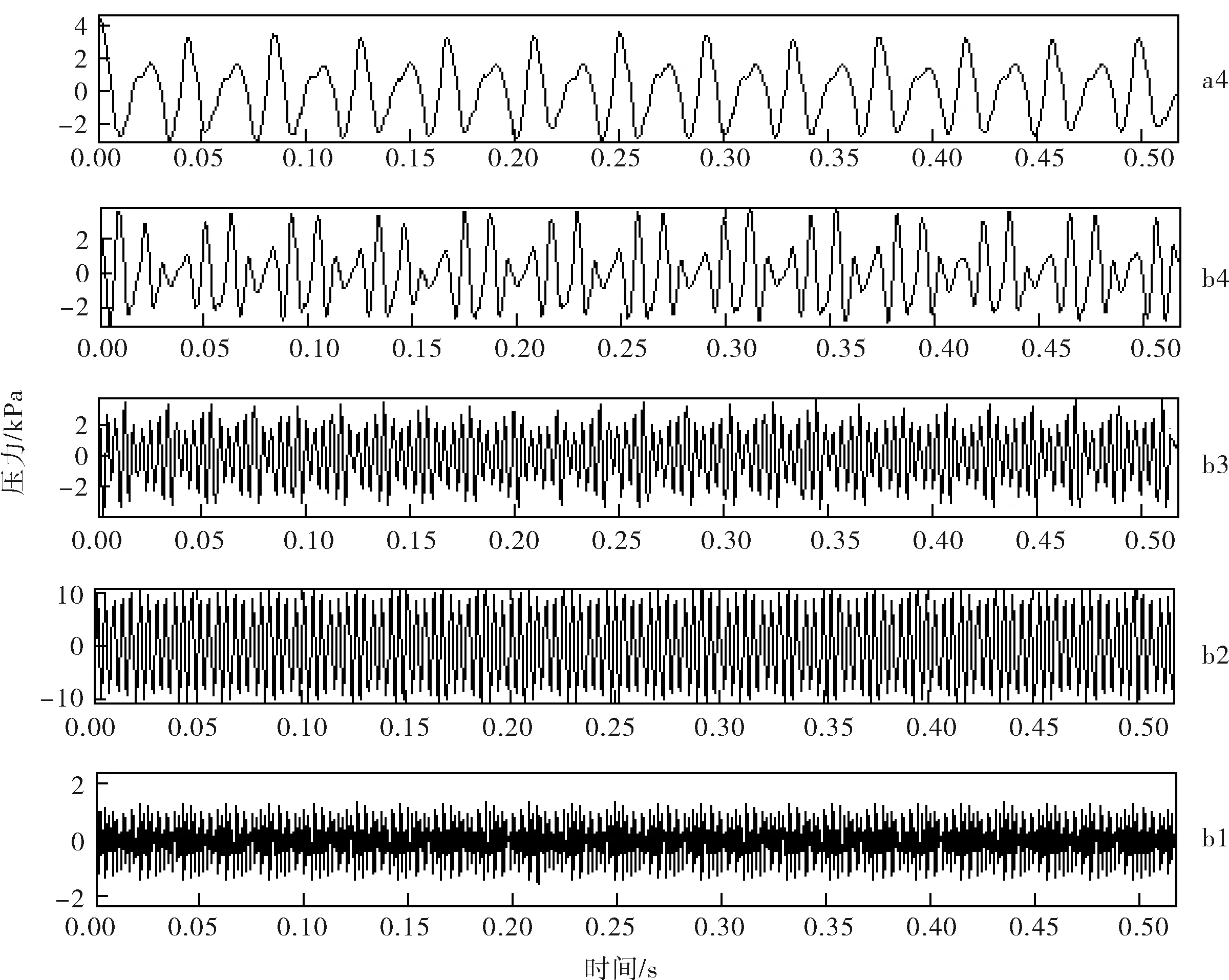
b． NPSHa=1.8m

1.3 时频矩阵奇异值分解

原信号Sj(t)被提升小波分解得到重构系数时频矩阵S并不能直接使用，需要利用奇异值分解算法(SVD)对其进行降维处理，在压缩数据的同时提取可以表达时频矩阵内在特征的参数量[13]。

时频奇异值分解步骤如下：

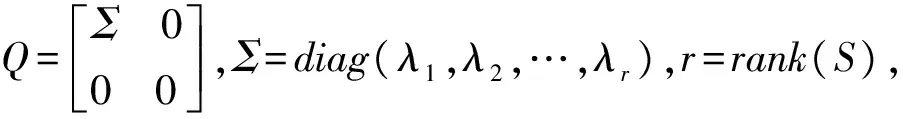
c. 提升db4小波重构系数组成的时频矩阵S包含压力信号Sj(t)完备信息，把这些不为零的奇异值降序排列成一维特征向量C=[λ1,λ2,…,λr]，此向量则唯一表征了时频矩阵，且反映了原信号Sj(t)的固有特征。

2 BP人工神经网络优化

2.1 优化方案

工程上，通常将BP神经网络分为输入层、隐层和输出层。在学习过程中，若实际输出与目标输出不符，则使用非线性可微分函数对权值进行调整，从而保证其非线性映射和泛化能力。但是标准BP网络的误差曲面多极小点很容易使训练陷入局部极小，影响精度与收敛速度，对早期汽蚀这类微弱故障的检测影响较大。

LM算法可以有效提高网络性能，使目标函数在接近最优点时，极值点附近的特性近似二次性，提高了寻找最优点的收敛过程[14]。优化网络节点权值时自适应调整梯度下降方法，调整公式为：

ΔW=-(JTJ+μE)-1JTα

式中E——单位矩阵；

J——误差对权值微分的雅可比矩阵；

α——误差向量；

μ——标量。

如果μ较大，LM算法接近于梯度下降法，而μ=0时LM算法则变为高斯-牛顿法，这样就很好地改善了收敛速度和泛化能力。

2.2 网络结构与参数

对优化后的BP神经网络进行详细的参数设置：输入层、隐层、输出层神经元数分别为5、13、3。通过全面的测试与比对，输入层到隐层的传递函数选择logsig()，隐层到输出层选择logsig()时的综合性能较好。训练的期望误差为1×10-4，最大训练步数5 000。

原始压力脉动信号共计28组，每组10段信号，其中NPSHa从1.5～ 4.0m区间每增长0.1m为一组，5.0、8.0、10.8m各一组。对所有信号进行提取特征处理，得到特征量后进行归一化处理，每组随机选择5段信号作为训练样本，剩余作为测试样本。分别设定正常工况、早期汽蚀工况和过临界汽蚀工况的目标输出为[1 0 0]、[0 1 0]和[0 0 1]。部分训练样本和目标输出见表1。

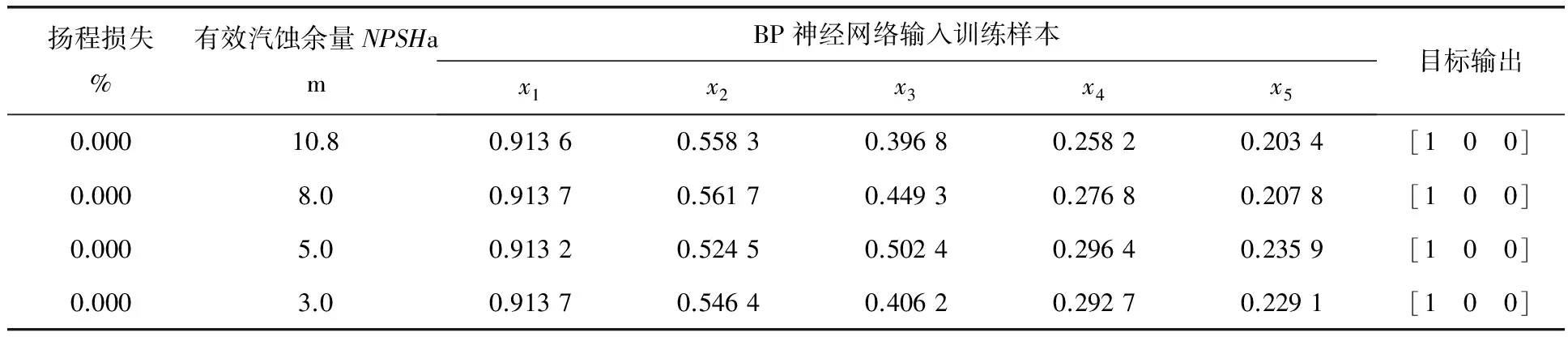
表1 不同有效汽蚀余量NPSHa下的特征量和目标输出

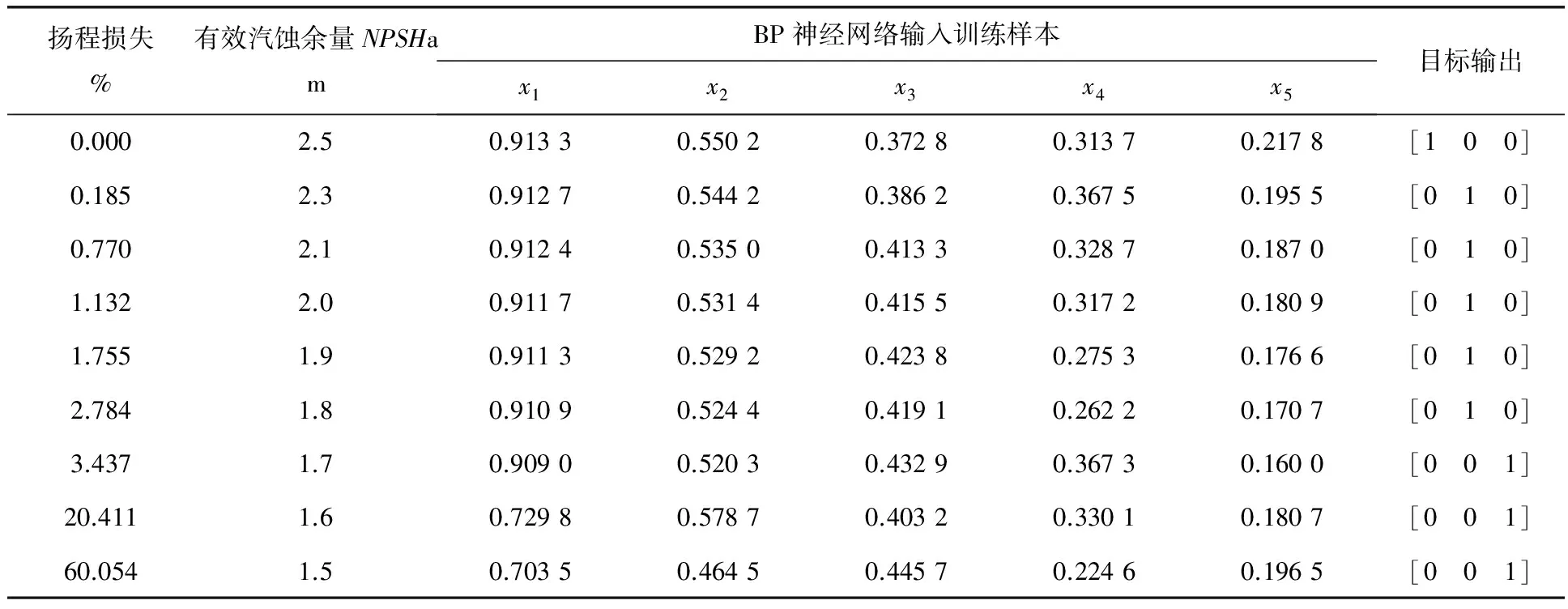
(续表1)

3 离心泵汽蚀故障诊断测试

网络测试样本为表1，所得输出见表2。

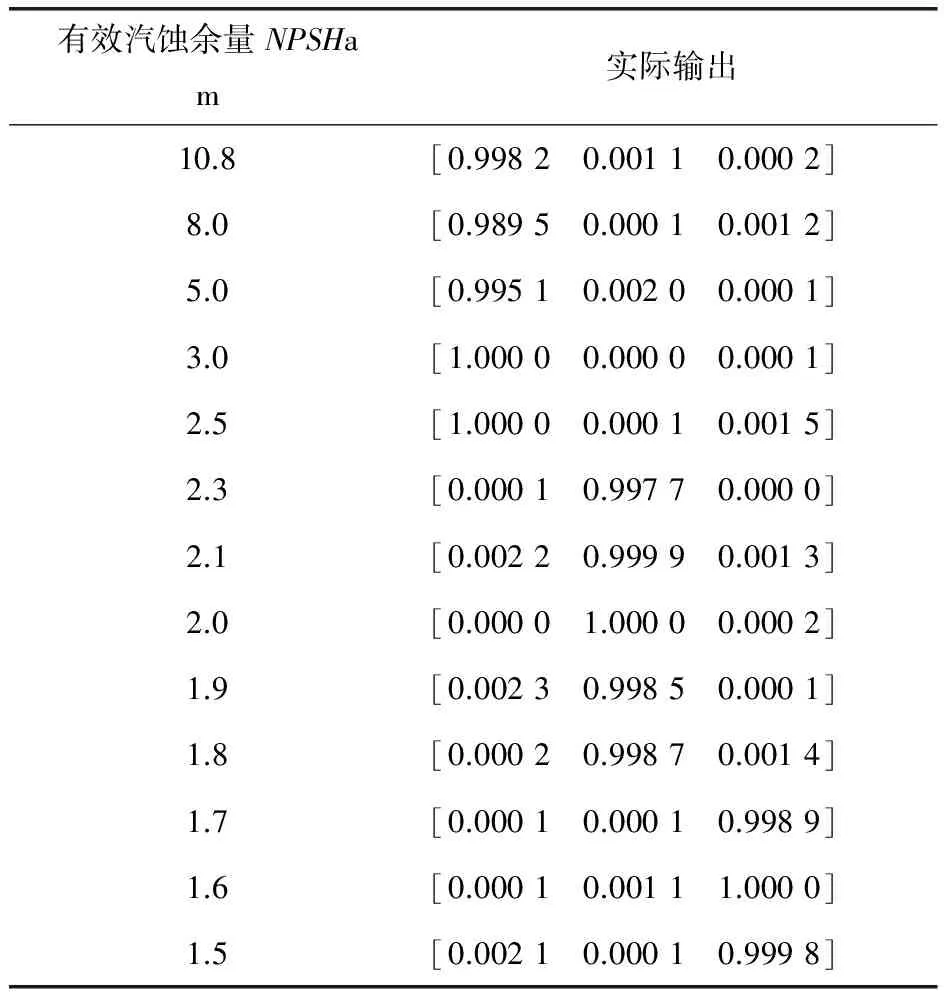
表2 神经网络输出值

将28组余下的脉动信号(计140段测试样本)输入到网络进行诊断，诊断正确率98.57%，其中NPSHa=1.8m组的一段信号被错误判断为过临界汽蚀故障，NPSHa=1.5m组的一段信号未能有效识别。

同样的数据，若使用无LM算法优化的神经网络诊断，正确率只有89.28%；若改用经典db4小波分解求得奇异值的正确率仅87.14%，且运算速度降低；而使用提升小波子空间能量谱来提取特征值的方案时正确率虽达到91.4%，但是在汽蚀各阶段的分界处诊断效果并不理想。

4 结论

4.1利用出口压力脉动信号可以对早期汽蚀故障进行诊断，提升db4小波比经典小波算法更适合提取非平稳、非线性特征，并兼顾了对信息描述的完整性与敏感性。

4.2奇异值分解理论可以应用在离心泵汽蚀故障诊断领域，奇异值特征比小波能量特征更可靠有效，反映流场的固有特征，非常适合判断汽蚀故障的各个阶段。

4.3经过LM优化的神经网络可以提高汽蚀故障的诊断正确率，以提升db4小波分解得到时频矩阵奇异值特征作为训练样本，诊断正确率高达98.75%，且在汽蚀各阶段交界处有良好的识别性能。该算法完全可以及时准确地对早期汽蚀故障进行诊断。

[1] 刘建瑞,高振军,郭晨旭,等.50IB-32型离心泵汽蚀性能的数值模拟与试验[J].排灌机械工程学报,2013,31(6):475～478.

[2] 张娜,张晶.离心泵汽蚀现象分析及防汽蚀措施[J].流体机械,2013,41(7):53～55.

[3] 牟介刚,张生昌,邓鸿英,等.离心泵汽蚀判据的研究[J].农业机械学报,2006,37(9):97～99.

[4] 周云龙,洪君,赵鹏.HHT与RBF神经网络在离心泵故障振动信号处理中的应用[J].热能动力工程,2007,22(1):84～87.

[5] 周云龙,郭柯.离心泵空化超声信号频谱特征研究[J].化工机械,2014,41(4):418～422.

[6] 王秀礼,袁寿其,朱荣生,等.离心泵汽蚀非稳定流动特性数值模拟[J].农业机械学报,2012,43(3):67～72.

[7] 周云龙,梁超.基于EMD能量熵的离心泵汽蚀故障诊断研究方法[J].化工自动化及仪表,2010,37(5):41～46.

[8] 刘阳,袁寿其,袁建平.离心泵的压力脉动研究进展[J].流体机械,2008,36(9):33～37.

[9] 周云龙,赵鹏,孙斌.基于提升小波包的离心泵故障诊断方法[J].热能动力工程,2011,26(6):738～742.

[10] 王松岭,刘锦廉,许小刚.基于小波包变换和奇异值分解的风机故障诊断研究[J].热力发电,2013,42(11):101～106.

[11] Daubechies I,Swekdens W.Factoring Wavelet Transform into Lifting Step[J].Fourier Anal APPl,1998,(4):245～267.

[12] 何为,杨洪耕.基于第二代小波变换和矢量量化理论的电能质量扰动分类方法[J].电网技术,2007,31(12):82～86.

[13] 李国宾,关德林,李廷举.基于小波包变换和奇异值分解的柴油机振动信号特征提取研究[J].振动与冲击,2011,30(8):149～152.

[14] 赵弘,周瑞祥,林廷圻.基于Levenberg-Marquardt算法的神经网络监督控制[J].西安交通大学学报,2002,36(5):523～527.