基于多尺度的形态滤波降噪方法

曹 莹 段玉波 刘继承

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

旋转机械的特征频率提取与故障诊断，是通过对机械设备振动信号进行一系列处理，提取能够表征机械故障的特征信息实现的。对于工程实际中所获得的机械设备故障信号而言，由于受设备工作环境等干扰，信号在采集和传输过程中会掺杂噪声干扰，影响后续的分析处理[1～3]。传统的信号降噪方法主要包括最优滤波、最优估计及自适应滤波等，但都有一定的局限性。

基于数学形态学的形态滤波理论是20世纪80年代初期被提出的一种高效降噪方法，在此主要在对形态滤波的基本原理和已有基于形态滤波的降噪方法进行分析研究的基础上，结合旋转机械振动信号的特点，提出基于多尺度运算的平均组合形态滤波降噪方法，并在仿真验证该方法有效性的基础上，将其应用于滚动轴承的特征频率提取中。

数学形态学是建立在积分几何及随机集论等严格数学理论基础上的数学方法，后来发展成一种新型高效的降噪方法。数学形态学包含腐蚀、膨胀、开运算和闭运算[4～6]。

设输入序列f(n)为定义在Df=(0,1,2,…,N-1)上的离散函数，结构元素g(n)为定义在Dg=(0,1,2,…,M-1)上的离散函数，且N≥M，则f(n)关于g(n)的膨胀、腐蚀、开运算和闭运算分别为：

(f⊕g)(n)=max[f(n-m)+g(m)]

(1)

(fΘg)(n)=min[f(n+m)-g(m)]

(2)

(f∘g)(n)=(fΘg⊕g)(n)

(3)

(f·g)(n)=(f⊕gΘg)(n)

(4)

基于这4种基本运算，通过不同的形态变换及其组合，可以产生不同的形态滤波效果。

Maragos采用形态学对开、闭运算进行级联，构造了形态开-闭Foc、闭-开Fco滤波器，定义为：

Foc(f(n))=(f∘g·g)(n)

Fco(f(n))=(f·g∘g)(n)

(5)

在此基础上，有学者构造了平均组合形式的形态滤波器，其输出信号为：

y(n)=(Foc(f(n))+Fco(f(n)))/2

(6)

还有学者将膨胀与腐蚀运算相结合，提出了基本形态差值运算，以同时提取信号中的正负脉冲，此运算所构造的滤波器输出信号表达式为：

y(n)=f·g(n)-f∘g(n)

(7)

形态滤波器的性能不仅与运算方法有关，同时还受结构元素影响，而结构元素的设计与选取主要取决于滤波后所要保持的信号形状。因此，在选取结构元素时，要尽量使结构元素的形状和尺寸(宽度、高度)与所处理信号相匹配，以提高信号的滤波效果。

目前，常见的结构元素主要有直线形、扁平形、三角形、椭圆形、正弦形、其他多边形及其组合形式。有学者针对旋转机械振动信号的时域波形特点，对不同结构元素的尺寸、形状对滤波性能效果的影响进行了分析研究。还有相关学者根据不同结构元素对不同噪声的敏感度不同的原理，采用多种结构元素组合级联方式，通过对每个级联部分采用不同的结构元素，并设置各部分相应的权重，得到不同滤波性质的滤波器[7，8]。

在采用形态学数字滤波器对旋转机械采样振动信号进行降噪滤波时，首先应根据实际振动信号基频周期内的采样点数和信号的最大振幅，合理选取结构元素的尺寸。应尽量选取宽度较小、高度在最大高度的0.15～0.22倍之间的结构元素，同时避免选择有尖顶的三角形结构元素。遵循上述规律合理确定结构元素的形状和尺寸，并按相应的运算方法构造满足要求的形态滤波器，可有效去除振动信号中的各种干扰，获得较好的滤波效果。

2 基于多尺度运算的平均组合形态滤波信号降噪

2.1 基于多尺度运算的平均组合形态滤波

根据相关原则，选择宽度为4的椭圆形结构元素。在此基础上，提出多尺度运算概念，假设G为形态学变换，则基于G的多尺度形态学变换可以定义为一簇形态学变换{GS|S>0，S∈Z}，即：

GS(X)=SG(X/S)，S>0

(8)

其中，SG为尺度S下的结构元素，是由G经过S-1次自膨胀或腐蚀运算所得。

基于多尺度运算概念，选定S=5，构造如下运算关系式：

(f·g)Sd(n)=(f⊕g⊕g⊕g⊕g⊕gΘgΘgΘgΘgΘg)(n)

(9)

(f∘g)Se(n)=(fΘgΘgΘgΘgΘg⊕g⊕g⊕g⊕g⊕g)(n)

(10)

式中Sd(G)——G经S-1次自膨胀运算所得；

Se(G)——G经S-1次自腐蚀运算所得。

在式(9)、(10)的基础上，通过平均组合运算，构造相应的基于多尺度的平均组合滤波器，其输出信号表达式为：

y(n)=[(f·g)Sd(n)+(f∘g)Se(n)]/2

(11)

2.2 仿真验证

为了验证基于多尺度运算的平均组合形态滤波器的降噪效果，将其应用于含噪仿真信号的降噪处理。给定含噪仿真信号为正弦信号与随机噪声的叠加信号，其中正弦信号的幅值为1，频率50Hz，噪声信号的强度10dB。仿真得到该含噪信号及其分量正弦信号的时域波形分别如图1、2所示。

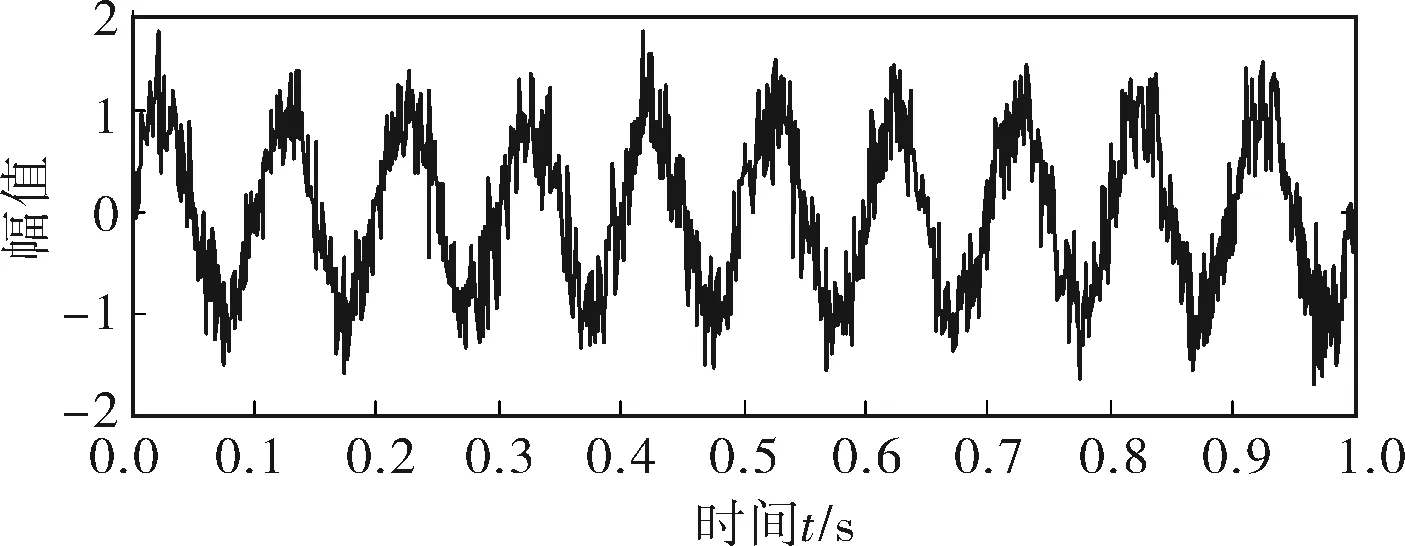
图1 含噪信号时域波形

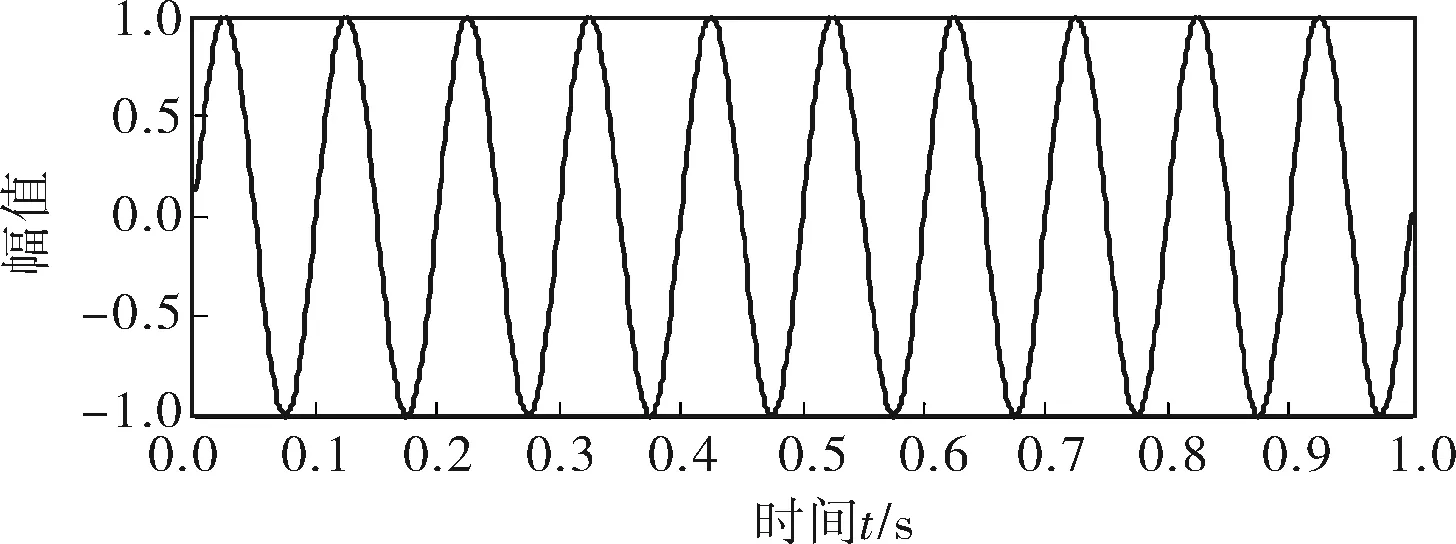
图2 分量正弦信号时域波形

利用基于多尺度运算的平均组合形态滤波器，对上述仿真信号进行降噪处理，并将降噪后得到的时域波形与原含噪信号的分量正弦信号时域波形进行对比，结果如图3所示。为了进一步说明该方法的有效性，对信号y进行传统降噪方法的仿真模拟，即采用平均组合形态滤波进行降噪处理(式(6))，降噪后得到的时域波形与原含噪信号正弦分量的时域波形对比如图4所示。

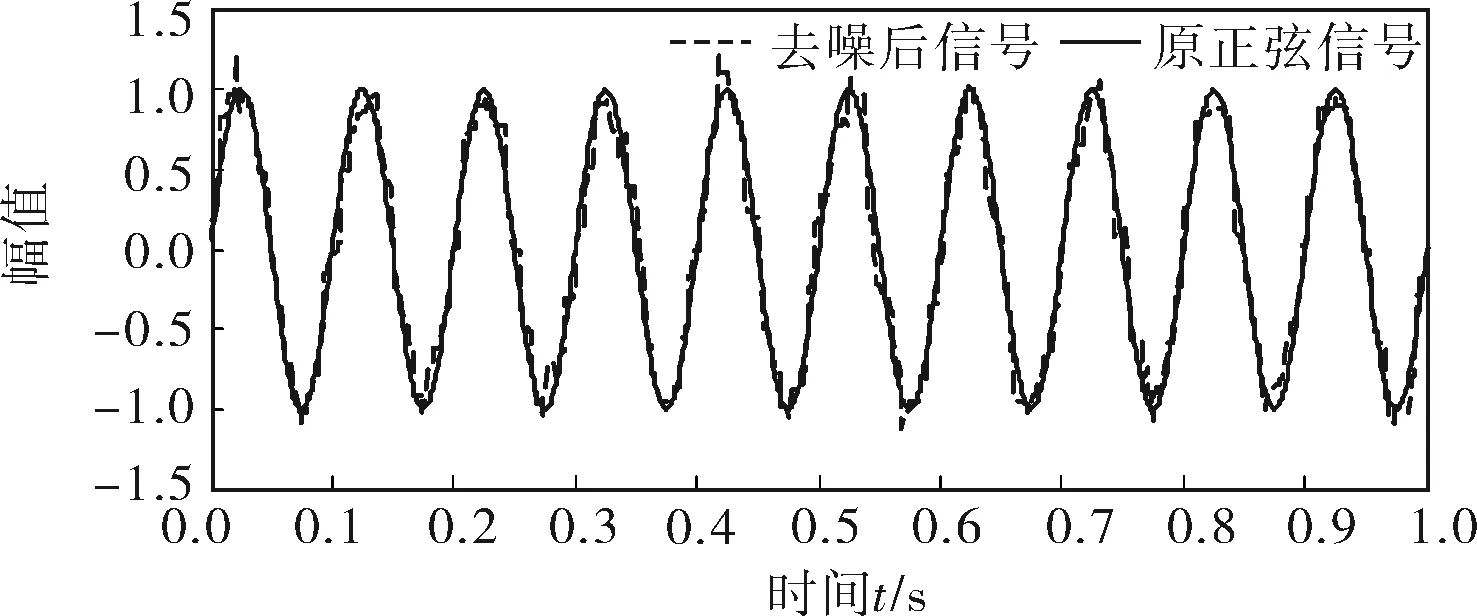
图3 笔者所提方法降噪信号与原正弦信号对比

图4 传统方法降噪信号与原正弦信号对比

对比图1、3，经笔者所提方法降噪后，随机噪声被大幅削弱，降噪后信号时域波形基本与原正弦信号时域波形吻合，波形整体较平滑，仅在个别数据点有尖凸，说明该方法具有较好的降噪效果。对比图1、4，经传统降噪方法处理后，随机噪声同样被大幅削弱，降噪后的信号时域波形与原正弦信号时域波形基本吻合，但波形整体不够平滑，尤其在峰值和低谷处更为明显。

3 实际应用

为了进一步说明笔者所提降噪方法在实际应用中的可行性和效果，将其应用于滚动轴承的故障特征频率提取中。

具体操作时，主体采用HHT方法，即通过对信号进行EMD分解和Hilbert变换，最终以Hilbert边际谱提取表征滚动轴承故障的特征频率。而笔者提出的基于多尺度运算的平均组合形态滤波降噪方法作为相应的信号预处理方法与HHT方法有机结合，最终实现对故障特征频率的有效提取。

试验中基本参数设置：电机转速1 730r/min、采样频率12kHz、采样数5 000点；轴承型号6205-2RS JEM SKF，内径25mm、外径52mm、滚动体直径7.94mm、轴承节径39mm、滚珠数9个。

根据上述参数设置，计算得到滚动轴承的转动频率28.83Hz，相应的故障特征频率分别为：内圈156.14Hz、外圈103.36Hz、滚动体135.91Hz、保持架11.48Hz。

首先，得到图5所示的待分析滚动轴承的振动加速度信号，并根据笔者所提降噪方法，对待分析信号进行基于多尺度运算的平均组合形态滤波降噪处理，得到处理后的时域波形如图6所示。对比图5、6可知，原待分析信号在经笔者所提降噪方法处理后，噪声幅值大为削弱，证实了该方法的有效性。

图5 待分析原始振动信号

图6 降噪后的信号时域波形

在此基础上，对降噪后的信号进行EMD分解和Hilbert变换，同时结合抑制模态混叠及端点效应等现象的端点延拓方法，最终得到图7所示的Hilbert边际谱。为了便于进一步分析，截取图7中0～1 000Hz的数据绘制相应的边际谱，如图8所示。

图7 降噪后得到的Hilbert边际谱

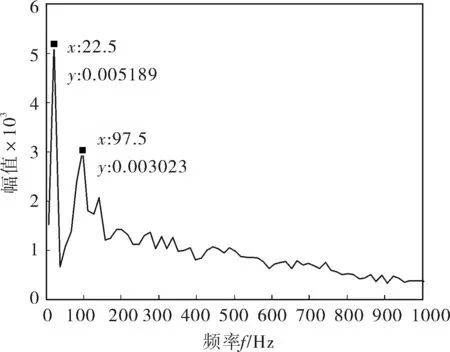
图8 降噪后的边际谱

为了分析说明笔者所提方法在实际特征提取中的有效性，将图5所示的待分析信号不经降噪处理，直接进行EMD分解和Hilbert变换，得到相应的Hilbert边际谱(图9)，由于噪声干扰，在Hilbert边际谱中振动信号本身的特征频率分量淹没在大量的高频噪声分量中，无法被准确清晰地提取出来。

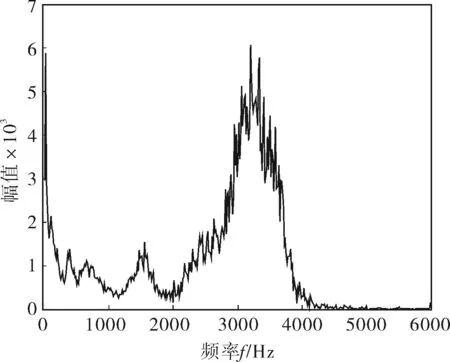
图9 未经降噪处理得到的Hilbert边际谱

对比图7、9，经降噪处理后得到的Hilbert边际谱中，高频分量被有效抑制。同时，图8所示的边际谱中清晰地显示出22.5、97.5Hz两个频率，虽然与实测振动信号的转动频率28Hz和外圈故障特征频率103Hz有一定误差，但相较于图9所示的提取效果而言，笔者提出的降噪方法能够与HHT有机结合，较好地分辨出信号的特征频率信息，进而诊断出滚动轴承的外圈故障。

4 结束语

笔者通过对数学形态学及其滤波原理和算法的分析研究，从运算方法和结构元素两方面研究了其对形态滤波器性能的影响。同时，通过对已有形态滤波降噪方法的分析研究，并结合旋转机械振动信号的特点，提出基于多尺度运算的平均组合形态滤波降噪方法。通过仿真模拟和结果的对比分析，验证了笔者所提方法的有效性。在此基础上，将其应用于滚动轴承的特征频率提取中，结果表明：该方法能够较好地去除滚动轴承振动信号的噪声干扰，为后续的信号分析和特征频率提取提供更接近原始真实信息的分析数据。

[1] 杨宇,于德介,程军圣.基于Hilbert边际谱的滚动轴承故障诊断方法[J].振动与冲击,2005,24(1):70～73.

[2] 苏文胜,王奉涛,张志新,等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击,2010,29(3):18～21.

[3] 曲从善,路廷镇,谭营.一种改进型经验模态分解及其在信号消噪中的应用[J].自动化学报,2010,36(1):68～73.

[4] 罗洁思,于德介,彭富强.基于EMD的多尺度形态学解调方法及其在机械故障诊断中的应用[J].振动与冲击,2009,28(11):84～86.

[5] 胡振邦,张东升,章云,等.数学形态学滤波器在转子失衡识别中的应用[J].振动、测试与诊断,2014,34(6):1038～1044.

[6] 刘继承,聂品磊,杨宏宇,等.基于形态滤波和HHT的滚动轴承故障特征提取[J].化工自动化及仪表,2014,41(5):529～532.

[7] 杜必强,唐贵基,石俊杰.旋转机械振动信号形态滤波器的设计与分析[J].振动与冲击,2009,28(9):79～81.

[8] 宋平岗,周军,陈建亨.形态滤波优化算法用于滚动轴承故障诊断[J].振动、测试与诊断,2014,33(5):756～762.